基于强激光场与固体靶相互作用的等离子体光栅产生新机制研究

袁丰毅 ,王加祥 ,黄渊凌 ,祝旭忠

（1.华东师范大学 精密光谱科学与技术国家重点实验室,上海 200241;2.华东师范大学 物理与电子科学学院 理论物理研究所,上海 200241）

0 引言

20 世纪80 年代啁啾脉冲放大(chirped pulse amplification[1],CPA) 技术的出现,让人们可以在实验室里产生超高场强的超短激光脉冲,这为强激光与物质相互作用研究带来了更多可能.在20 世纪90 年代,为了解释强激光与固体靶相互作用产生高次谐波,人们提出了振荡镜子模型[2].在该模型中,高强度的飞秒脉冲激光与固体靶相互作用,靶前表面的等离子体会在激光场的调制下随时间形成振荡密度周期分布,由此引出了人们对等离子体光栅的研究[3-4].1997 年,Plaja 等[5]通过理论分析和粒子(particle-in-cell,PIC) 模拟的方法,对使用两束交叉传播的强激光在临界密度等离子体表面形成光栅的设想进行了验证和分析,并给出了s 偏振光和p 偏振光在激发等离子体光栅时的不同效果.

进入21 世纪后,等离子体光栅的研究继续受到人们的关注.2003 年,Zhang 等[6]对两束飞秒强激光脉冲诱导的电子、离子密度光栅进行了数值模拟后发现,当采用的激光强度在 1 016W/cm2及以下,等离子体密度低于临界密度时,所获得的密度光栅峰值密度可达初始密度的数倍,且光栅结构则可以稳定数个皮秒.2009 年,Yu 等[7]探讨了低密度气体中光场电离产生的等离子体布拉格密度光栅,其工作中使用了强度为 1 013W/cm2的两束相向传播的激光脉冲,所产生的光栅相较于由激光强度在1015W/cm2通过有质动力驱动的光栅具有更长的寿命,约为纳秒级别.2010 年,Chen 等[8]通过数值模拟提出了移动电子数密度光栅(moving electron density grating,MEDG) 的理论,即当两束激光的频率差与等离子体频率相同时,会在等离子体内共振激发出大幅度的电子等离子体波,电子被激发后在泵浦光的干涉区形成一个移动的光栅状结构,而离子保持静止.2013 年,本文课题组发现使用强度为1015W/cm2的两束参数完全相同的相向传播的激光脉冲,在密度为0.004 倍临界密度的稀薄等离子体中,能产生随时间振荡的数密度光栅,此光栅不仅具有空间周期,还同时具有时间周期[9].

截至目前,大部分等离子体光栅都是基于双光束在低密度等离子体中的干涉来实现.对于超临界密度的固体靶,由于激光能量会被靶表面反射,因此很少有人会利用超临界密度靶来产生等离子体光栅.基于此,本文尝试利用强激光与超临界密度固体靶的相互作用,探讨在此条件下是否可以产生等离子体光栅.本文使用等离子体模拟中常用的PIC 模拟法,通过文献[10]开发的EPOCH 软件,对这一问题进行了1D-3V 的PIC 模拟研究.

本文后续结构: 第1 章给出计算的物理模型;第2 章对得到的数值结果进行分析和探讨;第3 章是结论.

1 物理模型

激光(laser) 和固体靶(target) 相互作用的示意图如图1 所示: 一束线极化的平面波强激光脉冲(laser pulse) 沿x轴从左向右入射到固体靶上.由于入射激光场的强度远大于靶的击穿阈值,因此目标靶在激光主脉冲入射时,已经被预脉冲进行了充分电离,从而可以直接用一个预等离子体来取代.模拟区域的左右边界均采用开放边界,即对于离开靶的激光与粒子,在到达边界时会被全部吸收.

图1 激光与目标靶相互作用示意图Fig.1 Schematic diagram of the interactions between the laser and the solid target

在计算中,设激光波长λ=400 nm ,脉冲强度I0=1015W/cm2,脉冲长度τ=3 ps ;目标靶选为氢等离子体靶,即由相同密度的氢离子(H+) 和电子(e-) 构成,靶的初始厚度d=0.2λ=80 nm ;初始密度n0=10nc,其中是等离子体临界密度,这里的me、qe分别是电子的质量和电荷量,ε0是真空介电常数,ω=2πc/λ,其中c是真空光速.

2 结果与分析

一般而言,对于密度低于临界密度的靶材,目标靶对激光是透明的.对于密度高于临界密度的靶材,激光场则会在趋肤深度内快速衰减,无法穿透目标靶而被靶的前表面反射.但是,当激光场强度(I)较高时,激光场产生的巨大光压会直接推动目标靶中的电子,引发表面电子和离子的振荡,进而将能量传递至靶内部.对I0=1015W/cm2的强激光,光压可以高达 1 0 GPa .

图2 给出了2 个不同时刻,激光在空间传播过程中电磁场能量密度(ε0E2+µ0H2)/2 的空间分布,其中,E是电场强度,H是磁场强度,ε0是真空介电常数,µ0是真空磁导率.图2(a) 表示,t＜0 时,激光在真空中传播.由于在计算中设定了t=0 为激光到达靶的前表面时间,因此t>0 后,激光才开始与等离子体相互作用.t=0.18 ps 时,从图2(b)可以很容易看出,电磁场的能量密度在靶表面趋肤深度的尺度上迅速衰减.这意味着,大部分激光场能量被靶的前表面反射.图2(c)显示了靶前表面附近的电磁场能量分布,从中可以看出趋肤深度δ≈20 nm,远小于激光波长,在这一区域内,电子和离子同时受到来自激光的指向靶内的有质动力,即光压的作用.由于质子的质量是电子的1 836 倍,所以相对而言,离子加速较慢,电子会先向靶内移动,引发电子和离子的空间分离,建立起电荷分离场.

图2 不同时刻激光场能量密度的空间分布Fig.2 Spatial distributions of laser field energy density at different times

图3 是激光作用到靶前后,电荷分离场的空间分布.从图3 中可以看出,t＜0 时,由于激光场还没到达靶表面,因此空间分离场为0.在t=1.33 fs 时,空间分离场的电场强度则高达 1 09V/m .此电场将使离子和电子发生比较强的耦合,即加速离子的同时会减速电子,进而引发离子、电子间的相对振荡.在靶材较薄时,即靶材整体厚度处于趋肤深度(δ)相当的厚度范围内,在激光强度和等离子体密度合适的情况下,离子将会被电子同步拉离目标靶,获得加速,即通常所说的稳相加速[11](phase-stable acceleration,PSA).而本文使用的是厚度为几百纳米的超临界密度厚靶,因此,激光引起的离子和电子之间的相互耦合振荡只能以声波的形式把能量传向靶内.为了看出这一点,先来研究一下目标靶内粒子数密度分布时间的演化,具体如图4 所示.

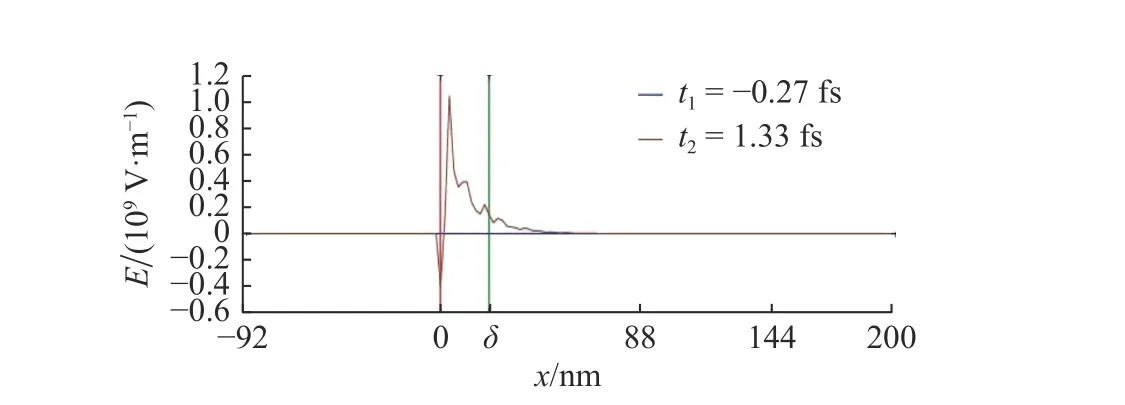
图3 不同时刻电荷分离场的空间分布Fig.3 Spatial distribution of charge separation fields at different times

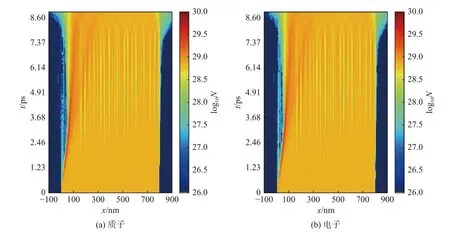
图4 目标靶质子和电子数密度的空间分布随时间的演化Fig.4 Time evolution of the spatial distribution of the number density of the proton and the electron in the target

从图4 可以看出,等离子体中质子(proton) 和电子(electron) 的动力学演化过程,其中N为其数密度(number density),用 l og10N表示其取对数后的数密度.从t=0 时刻开始,靶的前表面经过大约2.47 ps 的压缩后,靶的内部粒子开始出现数密度的周期分布;在达到t=2.67 ps 时,整个靶内已经能看出明显的光栅结构.从前面的分析可知,由于靶的超临界密度,激光在靶表面很小的趋肤深度附近就已经被反射,激光场能量没有直接传输到靶内部.但事实上,有部分激光场能量间接地通过电子和离子的振荡传输到靶内部.为了看出这一点,图5 计算了电磁场总能量(total field energy,Ef) 和等离子体中的粒子总能量(total particle energy,Ep) 随时间的演化.在图5(a) 中,Ef一开始随着时间不断上升,表示激光能量正在从左边界不断注入计算区域.中间一段时间,Ef近乎不变,这是因为入射激光能量注入的速度和从靶前表面反射回来的激光能量被模拟区域左边界吸收的速度几乎相等.最后,随着激光场能量停止注入,而反射激光仍旧在不断被吸收,整个模拟区域的光场总能量呈现出逐渐下降的变化.在整个激光从开始发射到停止发射的过程中,根据图5(b),很容易看出,等离子体的能量从0 时刻开始就在不断上升,直到不再有激光打到靶的前表面.这意味着激光场的能量在被靶表面反射的同时,不断被等离子体吸收.但激光能量的转化率或者吸收率比较低,约为10–4,即99.99%的激光能量都被目标靶反射,而正是这0.01%的转换能量促使了靶内部的等离子体密度光栅的形成.很显然,该光栅的形成和通常的利用双光束在稀薄等离子体内部的干涉产生光栅的机制有很大不同.

另外,由图6 还发现另外一个很有趣的现象,即电子和离子的数密度(N) 空间分布基本相同.因此整个光栅结构呈现出电中性的特性.这可以归结为电子和离子的长时间耦合振荡,导致了它们在空间的同步分布.从空间电荷效应会引发等离子体的不稳定性角度出发,也可以认为,只有这样的电中性分布,才能导致周期结构的稳定存在.该光栅的结构较为稳定,以至当靶的前表面已经被光压推向靶内部的时候,靶前表面的光栅仍能维持比较好的结构.图7 显示了图4 在靶前表面粒子数演化的局部细节图.从图7 中可以发现,该光栅的最高密度和最低密度可以保持为 3.77nc和 1 7.46nc,即26.276 9×1027/m3和 1 21.696 2×1027/m3,维持时长达到 5～6 ps .这一时间尺度可以用于对飞秒量级的强激光场进行调制.

图7 目标靶质子和电子在靶前表面数密度空间的时间演化Fig.7 Time evolution of the proton and the electron number density spatial distribution near the target surface

为了深入地了解等离子体密度光栅形成过程中的能量输运情况,图8 描绘了靶中质子和电子能量密度(ρE)的空间分布随时间的演化.显然,在相互作用开始的 1 ps 内,电子比离子更早获得能量,并在TNSA 机制下,带动离子一起运动.从 图8 中还很容易看出,获得加速后的电子和离子,基本停留在靶的前表面.只有少部分能量在经过约 0.6 ps 左右的弛豫时间后,很快传递到靶的后表面.这时,在靶内部,不但出现了稳定的能量分布,还能观察到和空间粒子分布相对应的周期结构.这表明,靶内的粒子以驻波的形式在发生稳定的振荡.由于激光脉冲在 3 ps 后,不再有光场能量持续输入,因此,该振荡是自持的,并且可以稳定地维持数皮秒的时间尺度.除此之外,将其与图6 的粒子数分布图对比,可以看到,在光压的作用下,靶的前表面等离子体在光压的作用下形成中性等离子体块结构,其粒子数密度高达 4 8nc=334.56×1027/m3,而且具有很高的能量密度.正是该致密等离子块阻止了强激光向靶内的传输.较为特殊的是,等离子块在被光压挤压的过程中,没有对已经形成的内部等离子体光栅产生明显的破坏作用,而只是保持在靶的前表面附近.随着时间的推移,它会不断膨胀,直到大约7 ps后,完全散开,发生能量向前后方向的耗散和传输.

图8 目标靶质子和电子能量密度的空间分布随时间的演化Fig.8 Time evolution of the spatial distribution of the energy density of the proton and the electron in the target

以上讨论的光栅对激光场强度有比较强的依赖.计算结果表明,当场强较大时,无法观察到光栅的形成.原因在于,当光压很高时,在光栅建立起来之前,靶内所有的电子和离子会一起加速离开,这一现象在激光等离子体加速中,已经被深入探讨过[11].若继续增加激光强度,光压甚至会在离子还没开始显著运动之前,就将电子直接推离靶材.为了防止这一现象的出现,根据前面探讨的光栅形成机制,只能采用更高密度的靶材来阻止激光进入或击穿目标靶.表1 给出了不同激光场强度和密度组合下,光栅的形成情况.从表1 中的数据可以得出3 点: 第一,在相同的靶材密度下,激光强度越高,光栅的空间周期越短,这意味着更高能量等离子体波的激发,但激光场强度高到一定程度,光栅将不能形成;第二,在相同激光场强度下,靶材数密度越高,越容易形成光栅,光栅的空间周期变短,趋肤深度也变小,与前面的理论分析基本一致,这意味着,在光栅能够形成的参数条件下,其空间周期还可以根据需要来做适当调节;第三,光栅的周期在纳米数量级,和离子之间的间距是同一个数量级,这再次表明,该光栅的形成来源于离子声波形成的驻波.

表1 不同激光强度和靶材密度下,趋肤深度和等离子体光栅周期的变化Tab.1 Changes in skin depth and plasma grating period under different laser intensities and target densities

3 结论

利用粒子模拟方法,本文发现利用单束强场激光脉冲(激光强度的数量级约为 1 015W/cm2) 与超临界密度等离子体(n≈10nc) 相互作用,可以在目标靶内部产生稳定的纳米尺度周期的数密度光栅.数值计算表明该光栅的产生主要源于强激光在靶内部激发的等离子体波的干涉.同时,本文还对光栅的形成对激光强度和靶材密度的依赖做了探讨,发现提高光场强度或靶材密度,可以降低光栅的空间周期.由于这一新型光栅出现在纳米和皮秒尺度,而 X 射线的波长范围处于 0.01～10 nm,该区间与光栅空间周期接近,故有望使用等离子体光栅来作为 X 射线的亚波长光栅;同时由于等离子体光栅作为新型光栅,其破坏阈值可能与传统光栅有所不同,因此,此光栅对未来 x 波段超短强激光脉冲的调制,会产生潜在的应用.作为一个有光栅结构的靶,在强场物理相关研究上的应用,也是接下去要研究的重点内容.同时还需要指出的是,在本篇工作中,仅针对一维情况进行了模拟研究.对于二维或三维等高维情况,如果在其他维度保持均匀,可以近似看成准一维的情况下,本文的模拟结果依旧具有重要的参考价值.在后续研究工作中,将对维度的影响进行进一步的探讨,为将来可能的实验验证提供更坚实的理论基础.