多段翼低雷诺数绕流涡-边界层相互干扰
王将升,王晋军
北京航空航天大学 流体力学教育部重点实验室,北京 100191
多段翼构型是现代大型飞机设计中常用的增升装置,是提高起飞重量、缩短起降滑跑距离、增强机场适应性的主要措施[1]。此外,很多新概念小型飞行器同样采用该构型来抑制失速,提升性能[2-3],其优化设计也因此成为先进飞行器设计的关键技术。然而,多段翼的绕流非常复杂,对飞行器的气动力、气动声学等特性具有重要影响,导致其优化设计存在较大难度[4-5]。前缘缝翼尾迹中的旋涡结构对主翼背风面边界层的干扰就是其中一个重要的复杂流动现象,由于主翼是多段翼构型的主要升力部件,此类涡-边界层干扰问题与飞行器的气动力特性密切相关,深入认识背后的流动机理能为多段翼构型和新概念小型飞行器的优化设计、控制流动分离提供理论依据。
众多研究者曾通过数值求解雷诺时均方程(RANS)[6-7]和激光多普勒测速(LDV)[8-9]从时均统计特性角度研究了前缘缝翼尾迹与主翼背风面边界层相互作用形成的混合边界层(Confluent Boundary Layer)。然而,他们并未关注混合边界层内的涡动力学特性,限制了对涡-边界层干扰流动机理的深入理解。
近期,Wang 等[10-13]针对特定迎角下(α = 4°)30P30N 多段翼低雷诺数绕流的精细实验测量表明(8.32 × 103≤ Re ≤ 5.2 × 104),主翼背风面的涡-边界层干扰随雷诺数增加会经历2 种模式。当Re ≤ 1.27 × 104时,前缘缝道内的弯曲流面通过离心力不稳定性在前缘缝翼尾迹中产生Görtler 涡,Görtler 涡通过激发流向条带的方式在主翼分离边界层内引入瞬态增长机制,进而触发旁路转捩,促进分离边界层的再附。随着雷诺数升高(Re ≥ 1.38 × 104),前缘缝翼尖端剪切层产生脱落的横向涡,横向涡会发生三维失稳并在前缘缝道流动的加速作用下被拉伸为类马蹄涡。最终,前缘缝翼尾迹同时包含流向涡(马蹄涡涡腿)与横向涡(马蹄涡涡头)。横向涡对应的扰动可在主翼前缘“浸入”(Penetrate)边界层并通过指数增长激发横向“双二次涡”(Doublesecondary Vortices)。随后,与流向涡对应的扰动通过“直接注入”和“间接诱导”2 种机制激发“双二次涡”的三维失稳并锁定其失稳波长,进而在边界层内产生马蹄涡,最终引起主翼边界层的旁路转捩。
在较高雷诺数下(Re ~ 106),前缘缝翼尾迹仍 同 时 包 含 流 向 涡 与 横 向 涡[14-16]。Pascioni 和Cattafesta[17]的实验测量与Satti 等[18]的数值模拟研究表明,与尾迹中横向涡对应的扰动可“浸入”主翼边界层并影响其后续演化。Li 等[19]近期的数值模拟研究发现前缘缝翼尾迹涡能在主翼边界 层 内 激 发 二 次 涡。Terracol 和Manoha[20]的 数值模拟研究则发现尾迹中的流向涡能在主翼边界层内激发流向条带。因此,前缘缝翼尾迹中的涡动力学特性以及缝翼尾迹涡与主翼边界层之间的相互干扰在一定雷诺数范围内(Re = 104~106)存在相似性。
除雷诺数外,翼型迎角同样是主翼背风面涡-边界层干扰的重要影响参数。时均统计结果表明,增大迎角会抑制前缘缝翼尾迹与主翼边界层的混合[6],但该混合效应背后的流动机理尚不明确。Wang 等[10]的实验研究发现迎角能通过影响前缘缝道内的弯曲流面来影响前缘缝翼尾迹中的Görtler 涡,进而影响主翼背风面的涡-边界层 干 扰。然 而,Wang 等[10]仅 讨 论 了 迎 角 对“Görtler 涡激发流向条带”干扰模式的影响规律,“尾迹涡激发双二次涡”干扰模式随迎角的演化特征尚不明确。因此,本文在Wang 等[10-13]前期研究的基础上,以30P30N 多段翼构型为研究对象,选取Re = 2.41 × 104为典型雷诺数,采用时间解析的粒子图像测速技术对主翼背风面流动开展精细测量,从时均统计和涡动力学2 个角度分析迎角(α = 8°, 12°, 16°)对“尾迹涡激发双二次涡”干扰模式的影响规律。需要指出,虽然实验测量的雷诺数较低,但是根据现有研究结果可知,本文揭示的流动机理仍然能为认识较高雷诺数下的涡-边界层干扰问题提供参考。
1 实验设备与模型
实验在北京航空航天大学低速回流式水槽中进行,实验段尺寸为3 000 mm × 600 mm ×700 mm(长×宽×高),来流速度U∞可在<500 mm/s 范围内无极调节,来流湍流度<1%。
实验采用的30P30N 多段翼模型是美国航空航天学会(AIAA)机体气动噪声标准模型计算大会的基准模型(图1),其收起状态下的翼型弦长c 为150 mm,展弦比为3.33。该展弦比以及翼型两侧的端板可保证翼型展向对称面附近流 场 的 准 二 维 性[14,17,21]。翼 型 迎 角α 定 义 为 主翼弦线与水平线之间的夹角,坐标系原点O 定义在α = 0°状态下的缝翼前缘,水平与垂直坐标轴定义如图1 所示。实验过程中固定U∞=161.3 mm/s,此时基于翼型弦长c 的雷诺数Re为2.41 × 104,考 虑α = 8°,12°,16°这3 个工况。
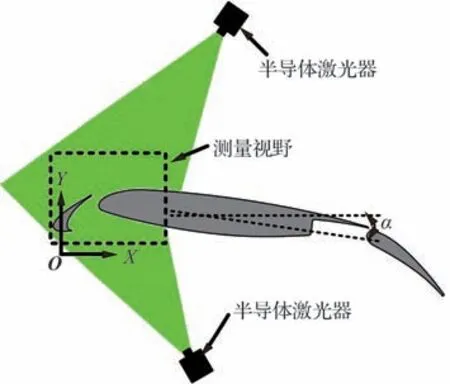
图1 30P30N 多段翼模型和实验装置示意图Fig.1 Sketch of 30P30N multi-element airfoil and experimental setup
2 实验测量与后处理技术
采用时间解析的二维粒子图像测速技术测量主翼背风面的复杂绕流,测量视野如图1 所示。前期研究表明[13],前缘缝道内的旋涡结构同样属于前缘缝翼尾迹涡,是主翼背风面边界层失稳的重要扰动源头,因此,测量视野中也包含前缘缝道区域。示踪粒子采用中值直径约为10 μm 的空心玻璃微珠。采用2 台半导体连续激光器(功率为8 W,波长为532 nm)产生厚度约为1 mm 的片光源,从上下2 个角度照亮测量视野内的示踪粒子。采用高速CMOS 相机从翼型侧面记录粒子图像,相机采样频率和图像放大率分别固定为720 Hz 和0.035 mm/pixel。
采用多通道迭代的光流算法(Multi-pass Iterative Lucas-Kanade algorithm, MILK)[22-23]从粒子图像中计算速度场,查询窗口大小为32 pixel× 32 pixel,窗口重叠率为75%。MILK 算法中固有的亚像素拟合与窗口变形可保证粒子图像位移的不确定度小于0.1 个像素,最终获得的速度场相对于自由来流的不确定度小于1.6%。
为深入揭示涡-边界层干扰的流动机理,采用有限时间的李亚普诺夫指数(Finite-Time Lyapunov Exponents, FTLEs)和傅里叶模态分解(Fourier Mode Decomposition, FMD)对速度场开展后处理。FTLEs 用于表征空间上相邻2 个流体质点在有限时间内其轨迹距离的变化率[24-25],其聚集区域一般被称为脊线,可用于提取拉格朗日拟序结构(Lagrangian Coherent Structures, LCSs)。FMD 通过对速度矩阵中的每一个速度序列进行单点离散傅里叶变换,可提供流场的全局功率谱密度和特定频率的空间模态[26]。对特定频段内的模态进行重构可获得该频段内的脉动速度场以及脉动速度强度[12-13]。
3 实验结果分析
3. 1 时均统计特性
不同迎角下前缘缝道和主翼前缘背风面的时均涡量云图与时均流线变化如图2 所示。图中:ωz为展向涡量;c 为翼型弦长;U∞为来流速度。主翼背风面边界层在α = 8°~12°范围内均处于附着状态,仅在α = 16°时出现大分离。在此迎角范围内,常见的单段翼 型背风面绕流(NACA0018[27]、NACA0012[28-29]及SD7003[30-32])普遍存在流动分离(Re ~ 104),下文分析将表明主翼背风面的涡-边界层干扰可增强边界层抵抗流动分离的能力,使其在α ≤ 12°的范围内保持附着状态。
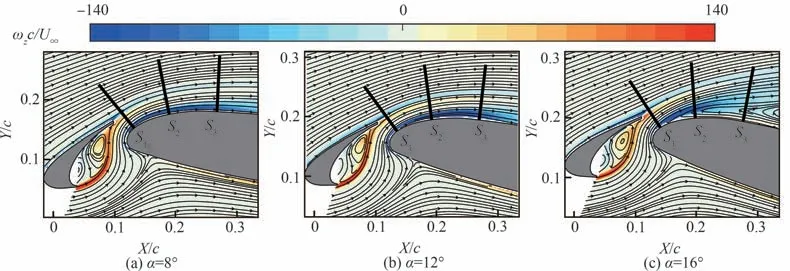
图2 不同迎角下时均涡量云图与时均流线Fig.2 Mean vorticity contours with superimposition of streamlines at different angles of attack
图3和图4 分别给出图2 中黑色采样位置(S1,S2,S3)处的时均合速度型(UHU∞)和脉动动能(K U∞2)以定量描述涡-边界层干扰的时均统计特性,其中YL/c 为采样点与主翼背风面之间的无量纲直线距离。为便于不同迎角之间的直接比较,3 个采样位置均垂直于主翼表面并且分别处于主翼的同一位置。与前期研究在α=4°时的测量结果[13]对比可知,S1位置处前缘缝翼尾迹对应的速度亏损(图3(a))和脉动动能峰值(图4(a))随迎角增大逐渐远离主翼背风面。当主翼边界层处于附着状态时,尾迹对应的速度亏损(图3(b)和图3(c))和脉动动能峰值(图4(b)和图4(c))沿弦向逐渐降低,但迎角越大降低越慢。Thomas 等[8]指出,当前缘缝翼尾迹中的速度亏损消失时缝翼尾迹与主翼边界层实现充分混合,因此,图3 和图4 结果表明,前缘缝翼尾迹与主翼背风面附着边界层之间的混合随迎角增大逐渐减弱,该现象也与杨茵等[6]在较高雷诺数下(Re = 9 × 106)的数值模拟研究结果一致。
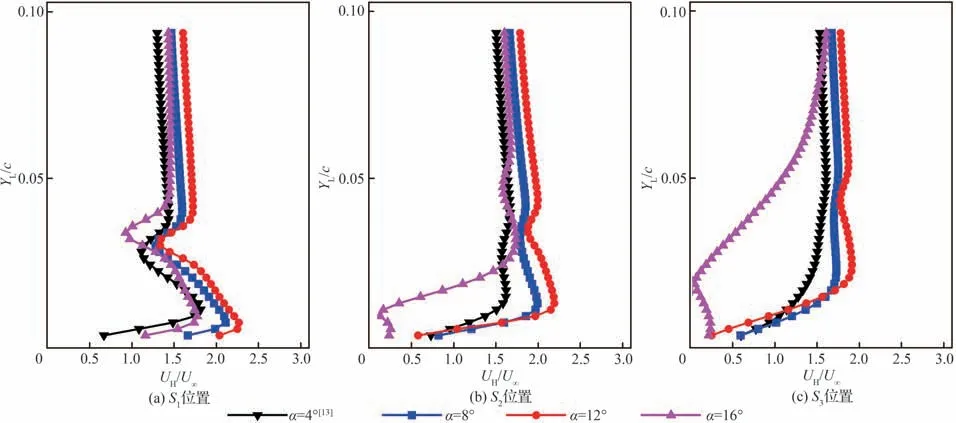
图3 不同采样位置的时均合速度型Fig.3 Mean resultant velocity profiles at different sampling positions
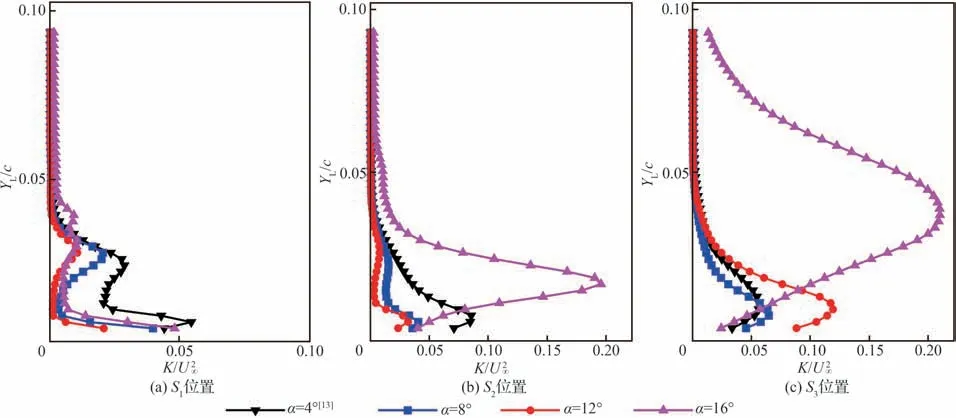
图4 不同采样位置的脉动动能Fig.4 Fluctuating kinetic energy profiles at different sampling positions
3. 2 涡动力学特性
图5所示为迎角α=8°下FTLEs 揭示的典型流动结构演化,其中T 对应典型流动结构的产生周期。缝翼尖端剪切层产生的横向涡在缝道加速流动的作用下会被拉伸变形,图5(a)表明变形后的尾迹涡在对流至主翼前缘上方时能在边界层内激发一个二次涡结构。在下一周期的尾迹涡激发二次涡之前,本周期内形成的二次涡的上游会产生一个更小尺度的旋涡结构。最终,一个尾迹涡能在主翼边界层内激发2 个不同尺度的二次涡,与前期研究在α = 4°时观测到的“双二次涡”结构[13]类似,本文也因此将图5(d)中箭头所示流动结构定义为“双二次涡”。此结构中的旋涡均为顺时针旋转,一方面能将缝翼尾迹区域的流体注入边界层进而促进尾迹与边界层的混合,另一方面能将边界层外区的高速流体注入近壁区进而增强边界层抵抗流动分离的能力。

图5 迎角α = 8°下的典型流动结构演化Fig.5 Evolution of typical flow structures at α = 8°
图6和图7 分别给出α = 12°,16°时的典型流动结构演化,可见在更大迎角下尾迹涡仍能在主翼背风面激发“双二次涡”。与前期研究在α =4°时的测量结果[13]对比可知,当主翼边界层处于附着状态时,“双二次涡”的产生位置随迎角增大逐渐沿弦向后移,对主翼前缘附近尾迹-边界层混合的促进作用以及流动分离的抑制作用逐渐降低,最终导致尾迹与边界层之间的混合逐渐减弱,主翼背风面边界层在α = 16°时发生大分离。
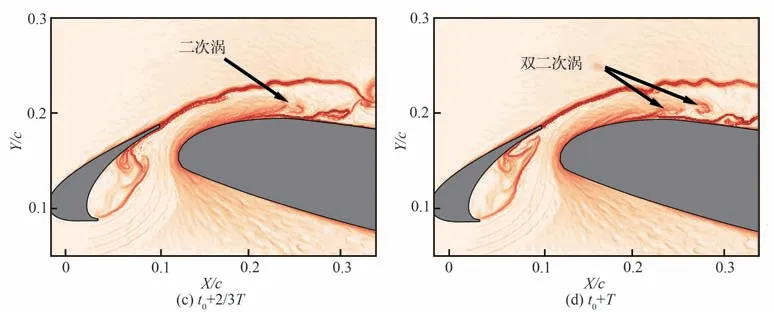
图6 迎角α = 12°下的典型流动结构演化Fig.6 Evolution of typical flow structures at α = 12°
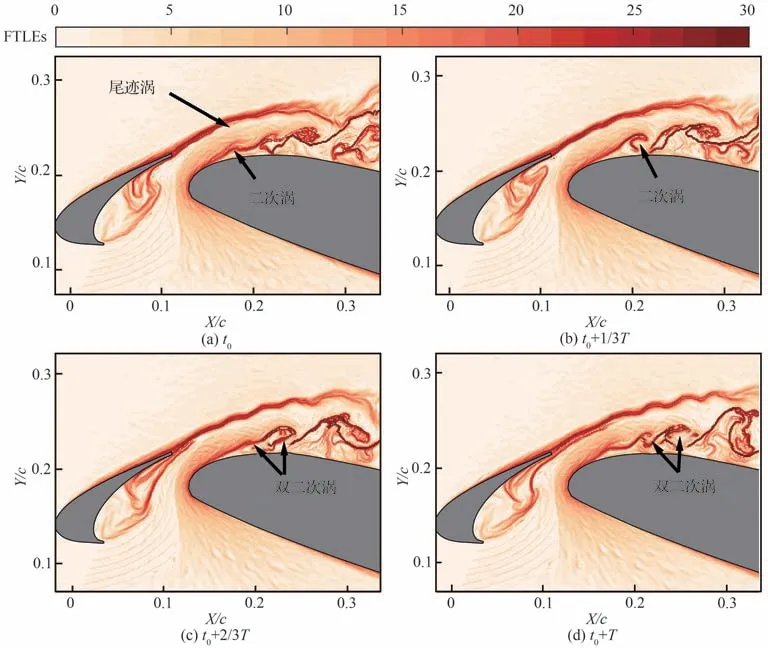
图7 迎角α = 16°下的典型流动结构演化Fig.7 Evolution of typical flow structures at α = 16°
为定量化描述涡-边界层干扰中的涡动力学现象,图8 和图9 对不同迎角下的流场开展了频谱分析。借鉴前期工作的研究思路[13],通过坐标变换将直接测量得到的脉动速度按照时均合速度方向的切向和法向进行分解,最终给出图8 所示的垂直于时均合速度方向的脉动速度强度分布(vrmsU∞),其中黑色圆点和蓝色十字均处于vrmsU∞的局部峰值。由图8 可知,缝翼尖端剪切层产生的旋涡结构在前缘缝翼尾迹区域引入较强的脉动速度,“双二次涡”结构则在主翼附着边界层内或分离边界层附近产生较强的脉动速度。从蓝色十字采样位置(P1、P2、P3、P4)提取垂直于时均合速度方向的脉动速度信号,利用傅里叶变换能获得脉动速度信号的频谱特性(图9)。可见,缝翼尖端剪切层产生的旋涡结构能产生具有多种特征频率的扰动(图9 中P1位置处的功率谱密度所示),包括基频(f1)、次谐波(f0.5)、分数谐波(f1.5)、二次谐波(f2)、三次谐波(f3)等。主翼边界层内的脉动速度同样具有多种特征频率(图9 中P2-P4位置处的功率谱密度所示),并且这些特征频率与前缘缝翼尾迹扰动的特征频率相同,表明前缘缝翼尾迹扰动能完全锁定主翼边界层内脉动速度的特征频率。

图8 不同迎角下垂直于时均合速度方向的脉动速度强度Fig.8 Intensity of fluctuating velocity perpendicular to mean resultant velocity vector at different angles of attack

图9 不同迎角下前缘缝翼尾迹与主翼边界层内的频谱特性Fig.9 Spectral properties of slat wakes and boundary layers above main element at different angles of attack
为进一步揭示前缘缝翼尾迹扰动与主翼边界层内脉动速度的联系,图10 和图11 分别给出α = 8°,16°时各特征频率对应的FMD 空间模态(仅考虑垂直于时均合速度方向的脉动速度),可见前缘缝翼尾迹中具有不同特征频率的扰动均能“浸入”主翼边界层并影响其内部流动结构的演化,但基频和二次谐波对应的尾迹扰动相比其他特征频率对应的尾迹扰动对主翼边界层的影响更大。需要指出,α = 12°时各特征频率对应的FMD 空间模态与α = 8°,16°时的FMD 空间模态类似,不再赘述。
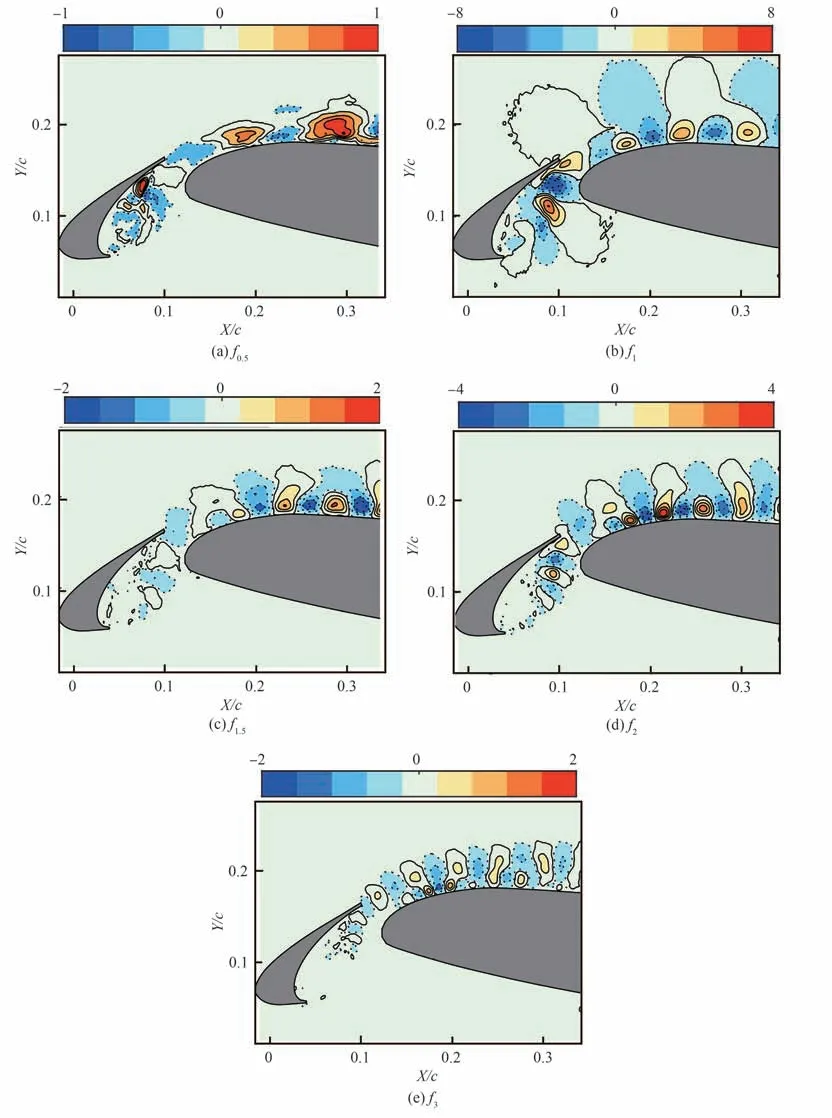
图10 迎角α = 8°下典型特征频率对应的空间模态Fig.10 Spatial modes of typical frequencies at α = 8°
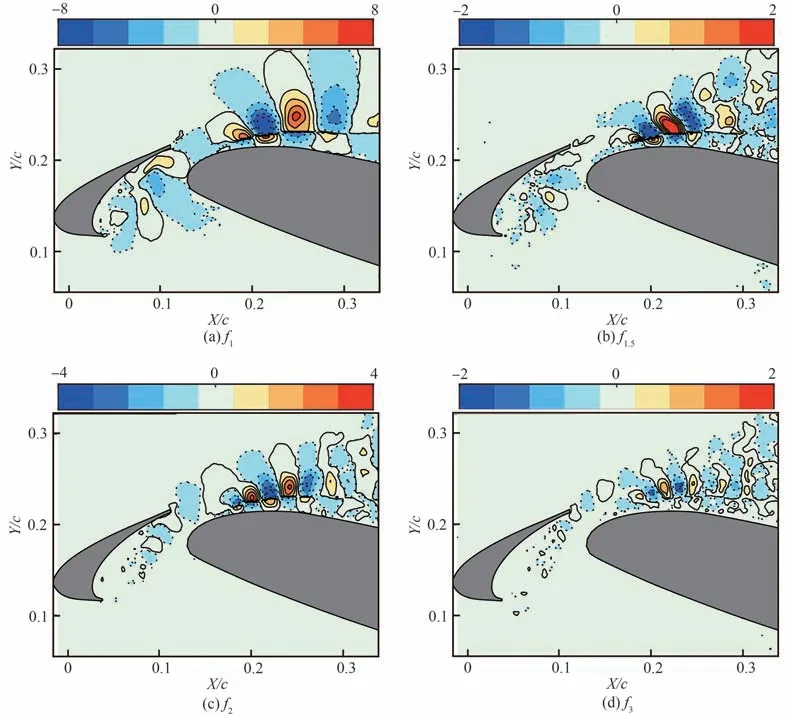
图11 迎角α = 16°下典型特征频率对应的空间模态Fig.11 Spatial modes of typical frequencies at α = 16°
虽然图10 和图11 中的FMD 空间模态表明基频和二次谐波是对涡-边界层干扰影响较大的2 个特征频率,但是这2 个特征频率对应的涡动力学现象能否主导主翼背风面的涡-边界层干扰尚不明确。为解答该问题,图12 和图13 借助FMD重构来更直观地展示这2 个特征频率对涡-边界层干扰的贡献。首先,借鉴前期工作的研究思路[13],在图9 中定义3 个频带BS、B1和B2,分别包含所有特征频率对应的脉动速度、基频对应的脉动速度以及二次谐波对应的脉动速度。随后,对BS频带、B1+B2频带、BS-B1-B2频带内的FMD 空间模态分别进行重构,获得不同频带内的脉动速度场,其中B1+B2频带的重构结果包含基频和二次谐波的共同贡献,BS-B1-B2频带的重构结果则包含除基频和二次谐波外其余特征频率的共同贡献。沿图8 中黑色圆点所示位置追踪原始脉动速度强度(vrmsU∞)、B1+B2频带对应的脉动速度强度、BS频带对应的脉动速度强度以及BS-B1-B2频带对应的脉动速度强度,最终给出图12 所示的扰动分频追踪结果。在“双二次涡”的形成过程中,主翼边界层内的vrmsU∞沿弦向快速增长,并且vrmsU∞的最大值随迎角增大逐渐增大。对比vrmsU∞和的增长趋势可知,BS频带内的重构脉动速度场可基本还原原始脉动速度场。 对比和的增长趋势可知,相比BSB1-B2频带,B1+B2频带内的重构脉动速度场对BS频带内的重构脉动速度场贡献更大。将B1+B2频带的重构脉动速度场与时均速度场叠加,然后计算所得流场的FTLEs,可得到图13 所示的典型流动结构,其中图13(a)~图13(c)所处时刻分别对应图5(d)、图6(d)、图7(d)所处时刻。对比图13 和图5~图7 可知,在仅考虑基频和二次谐波对应的脉动速度的情况下,即可复现主翼背风面的“尾迹涡激发双二次涡”现象。综上所述,虽然前缘缝翼尾迹涡产生的多频扰动均可“浸入”主翼边界层并影响其内部流动结构演化,但是基频和二次谐波扰动激发的“双二次涡”结构在此过程中占据主导。
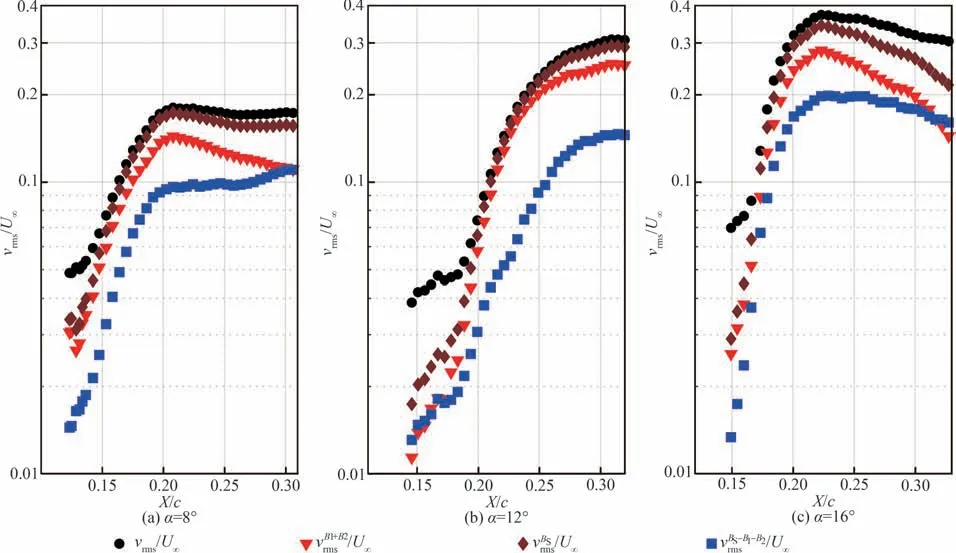
图12 不同迎角下“双二次涡”形成阶段主翼边界层内的扰动分频追踪Fig.12 Fluctuation tracking within different frequency bands during formation of double-secondary vortices at different angles of attack

图13 基频与二次谐波对应的重构流场中的典型流动结构Fig.13 Typical flow structures in reconstructed flow fields related to fundamental frequency and second harmonic
4 结 论
以30P30N 多段翼构型为研究对象,采用时间解析的粒子图像测速技术对不同迎角下的主翼背风面流动开展了精细测量,分别研究了主翼背风面涡-边界层干扰的时均统计特性和涡动力学特性并总结了迎角的影响规律,建立了时均统计特性与涡动力学特性之间的对应关系,得到以下结论:
1)对于时均统计特性,主翼背风面边界层随迎角增加逐渐由附着状态转变为大分离状态,在此过程中,前缘缝翼尾迹与主翼边界层之间的混合效应逐渐减弱。
2)对于涡动力学特性,前缘缝翼尾迹涡产生的具有多种特征频率的扰动在各迎角下均能“浸入”主翼边界层并影响其内部流动结构演化,其中基频和二次谐波扰动激发的“双二次涡”结构在此过程中占据主导。随着迎角增加,“双二次涡”的产生位置逐渐沿弦向后移。
3)从涡动力学的角度揭示了前缘缝翼尾迹与主翼边界层混合的机理:尾迹涡扰动首先“浸入”边界层并激发顺时针旋转的二次涡,二次涡的诱导作用能将更多尾迹涡扰动注入边界层,进而引起前缘缝翼尾迹与主翼边界层之间的混合;随着迎角增加,二次涡的产生位置沿弦向后移,对主翼前缘附近混合效应的促进作用逐渐降低,导致该混合效应逐渐减弱。
4)从涡动力学的角度揭示了主翼背风面边界层由附着状态转变为大分离状态的机理:二次涡能将边界层外区的高速流体注入近壁区,进而增强主翼前缘附近边界层抵抗流动分离的能力;随着迎角增加,二次涡的产生位置逐渐沿弦向后移,对主翼前缘附近流动分离的抑制作用减弱,最终导致主翼背风面边界层发生大分离。

