脉冲表面电弧放电对高超声速压缩拐角的非定常控制机理
丁博,陈真利,*,焦子涵,王锦程,李铮,白光辉
1.西北工业大学 航空学院,西安 710072
2.中国运载火箭技术研究院 空间物理实验室,北京 100076
随着超声速及高超声速飞行器的快速发展,对高速流场的控制能力需求日益增强,被动流动控制如涡流发生器、凹槽、陷窝等由于采用机械结构改变了气动外形,在超声速流场中通常响应时间较长,且容易带来非设计状态附加阻力。因此,主动流动控制技术逐渐成为超声速流动控制研究的热点。主动流动控制通过向流场中注入能量,按照需求对局部或全局流场进行调控。等离子体激励器作为主动流动控制装置,相比于被动流动控制具有无机械运动部件、响应时间短、重量和尺寸小、频带宽等优点[1],在过去20 年中进行了较多的研究。不同激励器具有不同的控制机制:组分改变、动量改变和能量改变,已成功用于从附着流到分离流、从层流到湍流、从低速到高超声速多种流动控制。
组分作用机制通过放电使流场中增加了新的粒子,如离子、电子、激发态粒子等。这些粒子的产生有可能激发系列化学反应,振动激发态粒子具有储存振动能并逐渐向平动能转化,持续时间较长,进而改变边界层性质的潜力。
动量作用机制是流场中电离形成的带电粒子在电场力的作用下加速并与中性分子碰撞,产生电流体力学(EHD)力,在近壁面诱导产生“离子风”。这类典型的放电形式有直流电晕放电[2-4]、交流介质阻挡放电[5-6]和脉冲直流介质阻挡放电[7]等。诱导产生的离子风速度约为几米每秒,将动量注入边界层底部使动量厚度增加,或诱导展向流动,可显著降低壁面摩擦阻力。Mhitaryan 等的研究表明,当离子风速为自由来流速度的20%~25% 左右时,可显著改变流动[8],Macheret 等的研究表明,要使EHD 效应显著,其相互作用参数ZEHD应大于0.1,该参数与来流密度与速度密切相关,密度与速度越大,EHD 作用参数越小[9]。因此,在高超声速流动中,来流速度很高,要实现较大的相互作用参数,需要很高的阴极电场强度。这在实际放电中很难实现。
能量作用机制主要是等离子体的焦耳热效应。放电过程中电能向内能转化,使局部气体压强和温度快速升高,甚至诱导激波并改变流场结构。这类典型的放电形式有直流辉光放电[10-11]、纳秒脉冲介质阻挡放电[6]、表面电弧放电、脉冲火花放电[12-15]等。直流辉光放电产生弱电离等离子体,具有局部焦耳热效应,可用于超声速激波调控和减阻,但其工作压强较低(0.1~10 Torr)。纳秒脉冲介质阻挡放电产生两种时间尺度的热效应。纳秒到微秒尺度的快速焦耳热形成压缩波和涡扰动。大于10 μs 时间尺度的慢焦耳热引起随机的涡扰动,可对流场进行调控。这种放电形式多用于跨音速和超声速流动控制。在腔体内的脉冲火花放电可形成等离子体合成射流将高温高压气体喷射到主流中,可有效穿透边界层,对超声速和高超声速流动具有显著控制作用,然而由于腔体内压力和密度恢复时间尺度较大,其放电频率难以提升。
为提高激励强度和放电频率,电弧放电是高速流动控制的较好选择。电弧放电等离子体激励器大致可分为3 类:局部电弧丝状放电等离子体激励器(Localized Arc Filament Plasma Actuator, LAFPA)[16-22]、准直流表面电弧放电等离子体激励器[6,23-30]和脉冲表面电弧放电等离子体激励器[31-34]。
LAFPA 最 早 由Samimy 等 在2004 年 提出[16],在电极之间施加幅值高达几千伏的脉冲电压形成电弧,电流强度约零点几安培,最大功率约100 W,考虑占空比后的放电平均功率约几十瓦,频率可高达200 kHz,产生热非平衡等离子体,振动温度约1 500 K,转动温度约600~800 K[16-17],形成微秒级局域热源,且激励器的频率、相位和占空比可单独控制,产生显著的局部压力及其对边界层的扰动,已成功地用于高速高雷诺数流动控制,如 射 流[18-19]、激 波 边 界 层 干 扰[20]和 空 腔 流动[21-22]等。为获得稳定可控的放电,需要把电极布置在凹槽内,会使飞行器表面不连续,同时由于放电功率较低、焦耳热效应强度有限,可控来流马赫数多在1~3 之间。目前尚未应用于高超声速流动控制研究中。
准直流表面电弧放电等离子体激励器由两个表面电极组成,放电时间较长约0.1 s。Leonov 等在马赫数2 自由来流下进行的大量试验研究表明,其典型放电参数为:放电电压约150~1 200 V,平均电流约1~10 A,平均功率0.3~5 kW/cm,电子密度约(2.0~4.5)×1015/cm³,折合电场强度约(10~100)×10-17V/cm²(10~100 Td)[6,23]。放电中可以看到清晰的电弧丝随流动向下游延伸并逐渐膨胀[24]。其运动速度接近主流速度的0.9 倍,单个电弧丝的持续时间约100 μs,长度接近50~100 mm,最大直径接近2 mm。在马赫数为2~2.5 的流动中,电弧丝震荡频率约10~50 kHz[6,23]。放电产生弱非平衡等离子体,在静压0.19×105Pa,等离子体功率7 kW 条件下,电弧丝的平动温度和振动温度分别为3 800 K 和8 000 K[25]。在高超声速流动控制研究中,多数试验中激励器布置在压缩拐角前,实现对激波的调控以及壁面压力的改变,以达到减阻或虚拟控制面的控制效果。试验中采用纹影和沿流向布置压力的传感器观察激波和壁面压力的变化。Leonov 等[6]的试验研究表明,压缩拐角处激波消失并在激励器处产生较弱的激波。Francois 等将其用与进气道唇口处,有效改变了激波位置,使非设计状态进气道调整到设计状态[26]。Watanabe 等对马赫数2 和马赫数4 的自由来流中压缩面上压力的研究表明,压缩面上压力降低,且压力和俯仰力矩系数变化量与等离子体功率呈线性关系。表面压力变化量和自由来流压力的比值与等离子体功率和来流焓值的比值也呈线性关系[27-29],从而可以通过改变等离子体功率实现对作用在模型上的气动力的线性控制。Watanabe 等对瞬态压力变化的研究表明,当电极距离压缩拐角30 mm 时,响应时间约0.2 ms,且与流速相关[30]。
脉冲表面电弧放电等离子体激励器的结构与准直流电弧放电相同,而电源不同。脉冲放电时间尺度在微秒量级,峰值电压约几千伏,峰值电流约200 A。多数试验研究压缩拐角处的激波边界层干扰控制。由于激励能量较大,脉冲时间短,存在很强电磁干扰,使得基于电信号的传感器和天平难以使用,导致气动力和表面压力定量测量非常困难。脉冲放电产生快速局部焦耳热形成高温气体团并诱导产生激波。甘甜等的研究表明,由于热气体团导致局部马赫数降低,使压缩面分离激波根部消失,上部分叉,并推测随着激波的减弱流动分离区会减小[31]。王宏宇等表明施加激励后分离激波的低频振荡有所改善,边界层涡尺度增大[32]。唐孟潇等的研究结果与此类似,并指出随着脉冲频率的提高,控制效果显著增强,而随着雷诺数的降低,控制效果减弱。他们认为高雷诺数下能量输运更强,更能抑制激波边界层干扰产生的逆压梯度引起的大尺度涡产生[33-34]。最新的研究表明[35],除了热气体团和诱导激波,放电还产生大量周期性流向涡和小尺度尾涡,促使混合增强和动量向边界层内转移,然而尚没有定量的试验数据证实这些推论。
存在几种常用的模型用于电弧放电等离子体流动控制:唯象学模型、双温模型和局部热平衡模型等。唯象学模型将电弧放电等离子体对流动的作用等效为局部热源,作为能量源项加入到流动的控制方程中,适用于准直流电弧放电和脉冲电弧放电。在准直流电弧放电的模拟中,采用的热源形状多种多样。Leonov 等根据试验观察和理论分析,将热源形状假设成楔形,并建立了楔角和等离子体功率之间的关系,但未考虑能量转变过程和能量损失,导致等离子体楔角偏高,激励区马赫数偏低[23,36-37]。Leonov 还将每个电极后的等离子体假设为长方体,模拟结果与与试验吻合较好,但模拟与试验中所用功率并不相同且没有直接关联[38]。此外,Francois 将电极后的等离子体区假设为圆柱形,并将其应用于非设计状态进气道调节研究中,推断试验与模拟的功率之间存在20%的误差[26]。Watanaba 等将上述圆柱模型后缘变尖,并用于马赫数7 来流下压缩拐角的非定常效应研究中。然而,所有的圆柱或类圆柱模型的尺寸选取标准不同,而且与激励器没有直 接 联 系[30]。Deshpande 和Poggie 提 出 了一种椭球模型,并发现等离子体激励会形成马蹄涡,激励的作用类似虚拟椭球面,使反射激波强度降低,表面摩擦系数略有降低,分离泡长度增加[39]。针对脉冲电弧放电的数值模拟研究较少。Sun 等进行了二维模拟,采用矩形热源,直接设定热源区内温度,验证了等离子体控制激波的热机理[40],再在热源区内施加能量,获得圆弧状压缩波,然而激波波形并不 正确[41]。Wantanbe 等考虑平动-转动和电子-振动-激发态的能量增加,采用Park 的 双 温 模 型[42]和Gupta 等 的11 物 种 模型[43]进行了估算,发现要模拟试验中压力变化,就必须考虑平动-转动能量转化的影响,而电子-振动-激发态能量的增加对压力影响小,但是对光发射强度的估算至关重要[44]。Poggie 等发现热力学非平衡现象显著地降低了能量沉积的效率,只有注入平动自由度的能量才能影响局部压力,且随着输入功率的增加热力学非平衡现象减弱了控制效果[45]。局部热平衡模型多用于电弧放电等离子体发展过程的模拟,尚未见用于流动控制研究中。
因此,为了揭示脉冲表面电弧放电等离子体控制高超声速压缩拐角流动的非定常机理,采用试验与模拟相结合的方法,研究脉冲电弧放电诱导的非定常激波形成机理及其形成的热气体团对高超声速典型双楔压缩拐角的控制能力。
1 试验设置
试验是在南京航空航天大学∅0.5 m 高超声速风洞(NHW)中进行的。NHW 是一座高压下吹-真空吸气暂冲式高超声速风洞,试验马赫数5~8,有效试验时间为7 s。NHW 风洞试验段为2 m×2 m×2.5 m 的方形半开口自由射流式,前端连接风洞喷管,喷管出口直径0.5 m,后端与扩压段相接,并在侧壁设有一对∅400 mm 的观测窗。在试验段一侧下方设有两个窗口供测压和测力信号线连接使用。试验中的自由来流参数见表1。

表1 自由来流参数Table 1 Free stream parameter
试验模型如图1 所示,包含前后楔两部分。前楔楔角为30°,高100 mm,宽40 mm。后楔楔角为15°,高18.935 mm,宽20 mm,安装在前楔表面后缘。模型前50 mm 为金属材料,后半部分为聚醚醚酮材料。

图1 试验模型侧视和俯视图Fig.1 Side view and planform of test model
在前楔表面沿展向布置了单个激励器,如图1所示。激励器由两个直径为1 mm 的铜电极组成,电极间距为5 mm,距前缘水平距离为63.38 mm。
试验用高速纹影系统进行流场观测。使用的 高 速CCD 相 机(Phantomv2512)帧 率 为25 000 fps,图像分辨率为12 80×800 像素,曝光时间为1 μs。
试验测压传感器采用压阻式压力变送器CYG1001,但由于试验中等离子体激励作用时间短(200 μs 左右),且放电过程中存在较强的电磁干扰,未获得有效数据。
试验采用南航自研∅20 六分量天平,其测力和力矩的误差均不超过0.2%,性能参数如表2所示。

表2 天平参数Table 2 Parameter of balance
测得放电电流电压数据如图2(a)所示。整个放电过程持续约20 μs,击穿电压约3 000 V,在击穿后0.1 μs 电压降至600 V,随后略微上升再下降,约15 μs 时刻降到零。试验中先用高电压击穿后,再用直流电源增大放电能量。电压出现负值是电容器放电后形成的反向充电。放电电流在10 μs 处达到峰值约150 A。整个放电过程的能量沉积如图2(b)所示,随时间近似呈线性增长,最终释放电能约0.34 J,不考虑电容器的反向充电过程。

图2 试验电流、电压和能量沉积波形图Fig.2 Test current, voltage and energy deposition waveforms
2 数值模拟方法
2. 1 脉冲表面电弧放电唯象学模型
文献中对准直流电弧放电数值模拟研究较多,针对低频高能脉冲电弧放电等离子体激励流动控制,电弧放电等离子体模型研究较少。为揭示脉冲表面电弧放电等离子体与流动的相互作用机制,首先建立了脉冲表面电弧放电等离子体唯象学模型。
Leonov 和Yarantsev[23]的试验表明,在 电 极两端的电压达到击穿电压时,电极间出现近似直的放电通道,随后在对流输运作用下,电弧丝向下游运动,运动速度接近0.9 倍当地流速。当电弧丝达到一定长度后断裂。新的等离子体丝在电极处重新形成,依据该放电现象建立了三维脉冲表面电弧放电唯象学模型。
电弧放电对流动的主要作用是局部焦耳热效应。因此,电弧放电与流场耦合的思路是将电弧放电等离子体的作用简化为空间热源项施加到能量方程中。
三维表面电弧放电模型基于如下假设:电弧丝截面是圆形,截面初始直径是电极直径的0.02 倍并随流动向下游运动,电弧丝直径随时间线性增加。电弧丝形状是由中点和电极控制的抛物线,且中点的运动速度为当地流动速度的0.9 倍;能量均匀的分布在电弧丝内。
在上述假设下,描述电弧丝运动的抛物线方程为
式中:xa=Uat 为电弧丝中点运动的水平距离,ya=Vat 为电弧丝中点运动的法向距离,Ua、Va分别为电弧丝运动的流向和法向速度也即当地流速的0.9 倍;xele表示电极距离前楔前缘的距离;zele=2.5 mm 表示电极距离前楔中线的距离,即电极间距的一半;α=30°为前楔的楔角。
描述电弧丝热功率密度的方程为
式中:Pa(x,y,z,t)为随时间和空间变化的焦耳热功率密度;P(t)为放电功率,由试验测量的电压与电流相乘得到;η 为能量转化效率;Va(x,y,z)为电弧丝体积。
电弧丝体积的计算基于如下假设:由描述电弧丝的抛物线方程积分得到电弧丝长度La,再乘以电弧丝截面面积Sa得到体积,即Va=LaSa。电弧丝截面面积表达式为
式 中:Ra=Ra,0+At 为 电 弧 丝 直 径,Ra,0为 电 弧丝截面初始击穿时刻直径,参数A 决定电弧丝直径变化的速率。此模型中,假设在放电结束时电弧丝直径线性增长到2 mm,与Leonov 等的试验一致[23]。
至此得到了热功率密度源项Pa(x,y,z,t),将其作为能量方程的能量源项进行求解,即可对脉冲表面电弧放电等离子体流动控制进行数值模拟。
2. 2 控制方程与数值方法
控制方程为
式中:ρ、p、T、U 分别为密度、静压、静温和速度;htot表示总焓;τ 和λ 分别代表 黏性应 力张量和 传热系数;Pa(x,y,z,t)为能量源项,即2.1 节所求的等离子热功率密度。
对计算方法进行了验证。验证模型采用双锥模型,如文献[46]中所示,来流状态为其中Run02 状态,其来流参数如表3 所示。采用有限体积法对控制方程进行数值求解,空间采用具有TVD 特性的二阶迎风格式进行离散,时间推进采用二阶隐式格式。

表3 来流参数Table 3 Free stream parameter
将数值模拟结果与试验结果进行了对比,并进行了网格收敛性验。 第1 套网格数为13.55 万,第2 套网格数为25.97 万,结果如图3所示,模拟结果与试验结果吻合较好,且2 套网格计算结果差别较小,证明了数值模拟方法的正确性。

图3 数值模拟结果与试验结果对比Fig.3 Comparison between numerical simulation result and test result
采用半模对双楔模型进行了数值模拟。对称面位于z=0,后楔侧面位于z=-10 mm,前楔侧面位于z=-20 mm 处,电极中心位于z=-2.5 mm 处。由于网格较为简单,只给出了对称面网格,如图4 所示,其中x 方向和y 方向的网格均间隔4 个点显示。壁面第1 层网格壁面距离为0.001 mm,对激波和放电位置进行了加密,电极附近网格尺寸为0.015 mm 以较好的捕捉电弧丝。拐角处网格尺寸0.015 mm,以较好的捕捉分离区。在电极间隙间进行了展向加密。来流条件与试验相同。入口和出口均采用超声速边界,壁面为无滑移边界。远场采用超声速出口边界。模拟分为两个部分,一是定常模拟获得稳定流场,二是施加激励后的非定常模拟。非定常模拟过程中,在施加激励20 μs 时间内,时间步长为5×10-9s,激励结束后时间步长逐渐增大到4×10-8s。

图4 计算网格(x 方向和y 方向均间隔4 个点显示)Fig.4 Simulation grid (4 points apart are displayed in the x and y direction)
3 结果与分析
由每个时刻试验测得的电流电压相乘得到功率P(t),再用六阶傅里叶级数对功率进行拟合,得到光滑的功率曲线,如图5 所示。参考文献[26,30,36-38]中采用的唯象学模型,选取焦耳热效率η=0.25。

图5 试验与数值模拟功率Fig.5 Power used in test and numerical simulation
采用第2 节建立的三维唯象学模型进行数值模拟。不同时刻的电弧丝如图6 所示,可清楚看出电弧丝在流动输运下的变形和抬升过程。

图6 不同时刻数值模拟的电弧丝Fig.6 Arc filament at different time in numerical simulation
不同时刻试验纹影与数值模拟纹影对比如图7 所示,在与试验时间相对应的数值模拟纹影上用圆点给出了试验纹影显示的激波位置。每帧之间的时间间隔为40 μs。数值模拟结果和试验结果吻合较好,表明建立的唯象学模型能准确模拟脉冲表面电弧放电等离子体产生的非定常流动控制过程。
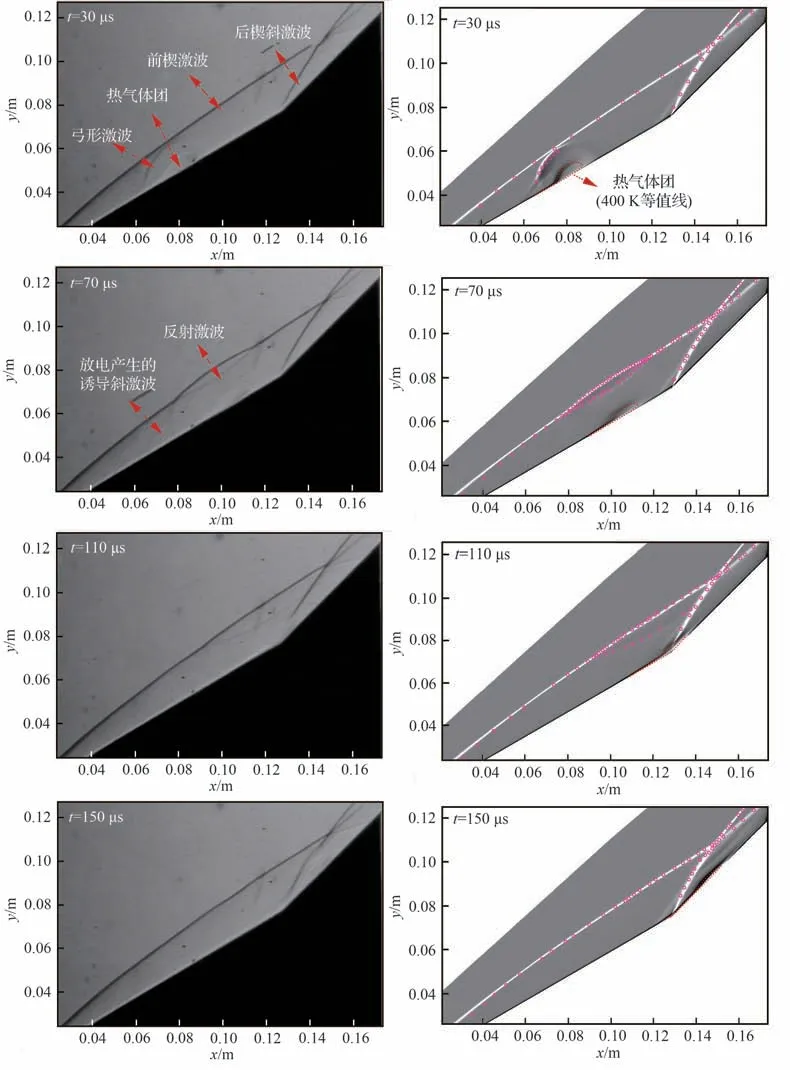
图7 试验(左)与数值模拟纹影(右)对比(数值模拟纹影中圆点为试验结果)Fig.7 Comparisons of test (left) and numerical simulation (right) schlieren images (test waves are shown as red circles in numerical simulation schlieren images)
3. 1 纹影波系对比
前楔与后楔分别产生一道斜激波,并在后楔上方交汇,如图8 所示,形成Ⅵ类激波-激波干扰。第1 帧中,在放电区域可以明显看到由局部加热产生的热气体团和局部高温高压形成的弓形激波,这是等离子体激励产生的第1 种激波扰动。由于第1 帧已经发展了一段时间,所以初始半圆形激波和高温区被拉长。弓形激波在流场中传播,其强度在传播过程中逐渐减弱。在第2 帧中可见弓形激波与前楔激波相互作用使前楔激波抬升,并出现反射激波。第2 帧中可见由放电诱导局部边界层分离产生的诱导斜激波,这是等离子体激励产生的第2 种激波扰动。诱导斜激波的运动与分离区密切相关,放电初始阶段伴随着分离区的扩大,诱导斜激波向上游略微移动。但是由于放电时间较短,分离区存在时间也较短,导致诱导斜激波存在时间较短且强度较弱。

图8 不同时刻热气体团与分离区的相互作用Fig.8 Interactions between thermal gas bulb and separation zone at different time
第3 帧中高温气体团运动到压缩拐角处,弓形激波和诱导斜激波几乎消失。可见拐角处后楔斜激波根部消失,而数值纹影中激波减弱并未消失。热气体团使局部温度升高,马赫数减小。在数值模拟中,后楔斜激波根部上游马赫数由初始的2.4 降低到1.2。
在第4 帧中高温气体团运动到后楔上方,后楔斜激波整体抬升,且颜色变浅。可推测后楔斜激波强度减弱,随着向下游运动的高温气体团温度降低,其对流场影响减弱。随着热气体团流过后楔,流场逐步恢复至初始状态。整个过程持续约160 ~200 μs。
纹影结果表明,表面电弧放电对流场主要有两种作用,一是产生两种激波扰动:弓形激波和诱导斜激波,并与前楔激波相互作用,二是高温导致局部马赫数减小,使后楔斜激波根部强度减弱。
3. 2 热气体团及其与分离区相互作用
在数值模拟中,当热气体团完全溢出边界层后,其向下游运动的速度在31~70 μs 时间内为676.25 m/s,在70~110 μs 时间内为578.12 m/s,与波后速度基本相同。这表明放电结束后,热气团在流场中以当地流动速度向下游输运,与试验中的第1 帧至第2 帧对应的速度613.42 m/s 和538.91 m/s 相一致。
当热气体团运动到拐角分离区时,如图8 所示,热气团采用400 K 等温线表示,分离区采用零速度等值线表示,可见热气体团并未进入分离区内,而是掠过分离区上方向下游运动。分离形态没有发生明显改变。
对称面(z=0 截面)不同时刻壁面压力与热通量的变化如图9 所示,在拐角处存在激波边界层干扰形成的分离区,在流向0.12~0.13 m 范围内,当热气体团运动到拐角时,可见分离区内壁面压力和热通量减小,这表明热气体团虽未能消除拐角处的激波边界层干扰,但是减弱了激波强度。正如图7 中110 μs 纹影所示,将后楔斜激波前的马赫数由2.4 降低到1.2。值得注意的是在130 μs 时热通量峰值比基本状态高,如图8 中130 μs 时刻所示,在x=0.13 m 位置处热气体团尾迹已进入分离区内,使壁面热通量增加。

图9 分离区附近压力和热通量分布Fig.9 Pressure and heat flux distributions near separation zone
图10给出了分离区与热气体团相互作用时的变化,可见分离点的位置变化很小,在106 μs和130 μs 时刻再附点向后移动,分离区长度分别增加了0.4 mm 和1 mm 左右。这是由热气体团的尾迹与分离区相互作用产生的。

图10 不同时刻表面压力系数云图和表面极限流线显示的分离区Fig.10 Contours of pressure coefficients and separateon zones indicated by surface limited streamlines at different time
3. 3 诱导斜激波产生机理
由于模型尺寸较小,雷诺数较小,形成较薄的层流边界层。
因为电极嵌入模型表面与模型表面平齐,所以放电产生的电弧丝出现在边界层内。电弧丝如何由边界层内输运到主流中,文献[47]提出了一种机制,认为电弧丝在边界层内诱导了涡的产生从而使电弧丝抬升到主流中。图11 给出了放电初始阶段电极附近的流场,此时电弧丝仍然存在,可以看到在靠近上游位置由于诱导产生的激波与边界层相互作用,在边界层内出现较大逆压梯度,出现分离,增大了当地边界层厚度,形成虚拟楔,产生斜激波。产生的斜激波位置随时间会发生变化,表明产生的虚拟楔随时间沿流向运动。单次激励下,因为热气体团很快运动到主流中,放电位置边界层内的逆压梯度消失较快,14 μs 时刻分离区基本消失,无法持续产生斜激波。

图11 放电初始阶段放电区域附近流场Fig.11 Flow field near discharge zone during initial discharge stage
同时为了定量度量电弧放电对边界层位移厚度的影响,取了电极附近几个位置,给出了边界层位移厚度随时间的变化曲线,如图12 所示,边界层位移厚度为

图12 不同流向位置边界层位移厚度随时间变化Fig.12 Variations of boundary-layer displacement thickness at different streamwise positions with time
式中:δ*为边界层位移厚度;由于前楔有30°倾角,因此将式(5)中的速度u 取壁面方向速度;y 为壁面法向距离;ρe、ue分别为波后的边界层外的密度和速度。
可见放电后放电位置的边界层位移厚度明显增加,并且在相同时刻,位置越靠后位移厚度增加的越明显。这表明电弧放电导致边界层位移厚度增大,形成虚拟楔并诱导斜激波的产生,如图13 所示。可以推断,如果提高放电频率,使边界层位移厚度保持在较高水平可以产生较为稳定的斜激波,与准稳态放电的效果相似。
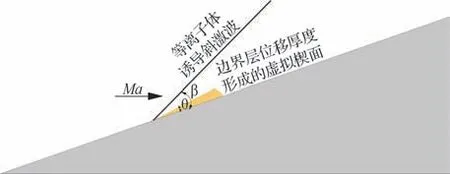
图13 虚拟楔及其诱导斜激波示意图Fig. 13 Sketch of virtual wedge and its inducing oblique shock wave
由于放电产生的分离区内不同位置边界层位移厚度不同,采用分离区内两个不同位置的边界层位移厚度可求得不同时刻虚拟楔的楔角,如图14 中红色曲线所示。可见在3.6 μs 之前由于能量的持续注入,虚拟楔面楔角值近似线性增加,在3.6 μs 达到最大值6.7°。随后输入能量下降,楔角也逐渐减小,在4.8 μs 之后楔角近似线性下降。

图14 不同时刻虚拟楔角及其对应诱导激波角数值模拟与理论值对比Fig.14 Angles of virtual wedge and comparison of its numerical simulation and theoretical corresponding shock wave angles
Leonov 和Yarantsev[23]在准定常电弧放电中给出了虚拟楔角与其产生的斜激波角关系,即θ-β-Ma 关系式:
式中:θ 和β 见图13。由式(16)计算得到斜激波角的理论值,与数值模拟结果对比如图 14 所示。可见,数值模拟中得到的斜激波角与理论值基本一致,这表明斜激波是由放电使边界层位移厚度增加形成的虚拟楔产生的。
3. 4 三维结果
目前国内外对表面电弧等离子体流动控制三维流场分析较少,造成对热气体团的展向分布和激波横向控制效果不清楚。图15 给出了不同时刻对称面和壁面垂直截面内的温度云图,截面位置为图15(a)中黑色虚线表征。可见不同截面内热气体团的形状均为中间较厚两侧较薄,边界约在z=0.01 m 处,约是电极间距的4 倍。热气体团在展向分布并不均匀,因此如果在展向形成较大范围控制,必须考虑单个激励器产生的热气体团所能影响的最大区域,这对于优化激励器展向布置具有一定指导意义。

图15 不同时刻对称面和垂直壁面展向截面温度分布云图Fig.15 Temperature contours of symmetrical and wall-normal cutting sections at different time
在图15(b)中可见清晰的展向反射激波。反射激波在展向几乎是平直的。红色线框内可见前楔激波被抬升,44 μs 时刻展向影响范围达到0.01 m,56 μs 时刻达到0.018 m,68 μs 时刻达到0.022 m,可见随着弓形激波的发展,其在展向的影响范围也在逐渐增大。随后随着弓形激波的减弱,对前楔激波的抬升作用基本消失。这表明弓形激波在展向的控制范围有限。注意到激波被抬升的幅度在对称面处最大,间接表明弓形激波的强度在展向向外衰减。
3. 5 表面力和热流变化
壁面压力系数分布云图如图16 所示,红色虚线大致给出了压力系数有明显变化区域的运动轨迹,可见在5 μs 时刻由于放电产生的局部高压强使壁面压力系数突然增加,随后在25 μs 时刻x=0.08 m 位置处壁面压力系数降低,同时在x=0.09 m 位置处存在弧形高压力系数区域,这是弓形激波与壁面相互作用产生的。在124 μs 时刻可见后楔压力系数减小。同时压力系数变化区域的运动轨迹与前述热气体团的运动轨迹一致,表明压力变化是由于局部加热带来的气体膨胀产生的。

图16 不同时刻壁面压力系数分布云图Fig.16 Contours of wall pressure coefficient at different time

z=0 mm、z=5 mm 处的壁面压力沿流向分布如图17 所示。可以看到在放电初始阶段5 μs时刻,z =0 mm、z =5 mm 均存在压力的突增,随后出现小范围内的压力降低,如前所示,这是因为放电产生的热气体团使局部气体膨胀导致气体压力和密度降低。压力降低区域下游存在压力较高区域,这是由弓形激波前沿与壁面作用产生的。壁面存在压力降低区域,与文献[27-29]结果一致。图17 中标出了25 μs 时刻的压力降低值,可见z=0 mm、z=5 mm 两个时刻最大压力降低幅度基本一致,约为25.0%。随着热气体团强度减弱,壁面压力降低值也在减小,由此可见壁面压力降低与热气体团和弓形激波的运动存在密切的关系。

图17 不同时刻两个展向位置截面壁面压力及压力系数分布对比Fig.17 Comparisons of wall pressure and pressure coefficients of two spanwise positions at different time
中截面处壁面摩擦系数(Cf)和传热系数(Stanton 数)分布如图18 所示,可见在25 μs 时刻流向0.075~0.087 m 范围内摩擦系数减小,52 μs 时也有略微减小。Stanton 数的分布与之类似。这表明表面电弧放电等离子体激励可用来降低特定位置摩阻和传热。在52 μs 之前壁面摩擦系数和Stanton 数均存在大幅升高区域,在实际应用时应综合考虑。

图18 不同时刻中截面摩擦系数和Stanton 数分布Fig.18 Friction coefficient and Stanton number distributions of symmetrical cross-section at different time
模型所受轴向(x 方向)力和法向(y 方向)力如图19(a)所示,由于模型没有迎角,可等效为阻力和升力。0 μs 时刻为激励开始时刻。

图19 不同时刻轴向力、法向力和俯仰力矩系数变化Fig.19 Variations of streamwise, normal forces and pitching moment coefficient at different time
施加等离子体激励后存在局部高压,使阻力迅速增加,随着电弧丝被抬升到主流中和壁面压力的下降,阻力开始减小。在110 μs 时刻阻力最小,降幅约2%。可见在30~50 μs 时间内,阻力的下降率发生变化,这是因为在展向弓形激波超出模型宽度。在60~74 μs 时间内阻力小幅增加,这是由于靠近下游的弓形激波与后楔和后楔斜激波相互作用产生的。随后由于弓形激波强度的减弱,模型所受合力进一步减小,在最低点由于运动到后楔的热气体团较弱,流场逐渐恢复到初始状态。俯仰力矩系数随时间变化如图19(b)所示,可见在基本状态下俯仰力矩系数为0.77,与试验值0.74 对比相对误差为3.95%。力矩变化趋势与合力变化趋势一致,俯仰力矩系数在110 μs 时刻最小,降幅约3%。上述分析表明脉冲表面电弧放电激励能够起到改变壁面压力获得减阻和改变俯仰力矩的控制效果。
4 结 论
1)建立了脉冲表面电弧放电唯象学模型,数值纹影与试验纹影吻合,能够较准确模拟电弧丝与流动之间的相互作用过程,验证了唯象学模型的正确性。
2)非定常数值模拟结果揭示了脉冲表面电弧放电等离子体与高超声速双楔流动相互作用机理。放电产生局部焦耳热诱导形成近壁分离区,导致局部边界层位移厚度的增加,形成沿壁面运动的虚拟楔。理论值与模拟值的对比证实诱导斜激波是由虚拟楔产生的。
3)试验和数值模拟结果都表明脉冲表面电弧放电产生热气体团并诱导产生弧形激波。热气体团使流动局部温度升高,马赫数减小,后楔斜激波根部强度减弱。弧形激波与前楔激波之间形成包括激波反射在内的非定常激波/激波相互作用,使前楔激波抬升,显示脉冲表面电弧放电对激波有明显调控能力。
4)对气动力和俯仰力矩的分析表明,脉冲表面电弧放电等离子体能有效降低壁面局部压力,壁面压力最大减小25%。单次激励下,最大减阻量约2%,最大俯仰力矩变化量约3%。

