航空发动机排气系统单站RCS 准确高效仿真方法与试验验证

陈新蕾，卢立昌，吉洪湖，顾长青，高帆，施小娟

1.南京航空航天大学 电子信息工程学院 雷达成像与微波光子学教育部重点实验室，南京 211106

2.南京航空航天大学 能源与动力学院，南京 210016

航空发动机排气系统是典型的腔体结构，是战斗机后向雷达散射截面（Radar Cross Section， RCS）的主要散射源之一［1-4］。有效降低排气系统的RCS 是提高作战飞机隐身能力和作战能力的一项重要措施。而在对发动机排气腔体进行隐身设计的过程中，对其电磁散射特性进行准确高效的仿真计算是一个重要的环节。

发动机排气系统内部具有复杂结构，散射物理过程具有多次反射的特点，是电大散射问题，其面临着准确求解计算量大、计算时间长的问题。针对这些问题，本文研究排气系统电磁散射问题的准确快速求解算法。

目前用于排气系统电磁散射计算方法主要有弹跳射线法（Shooting and Bouncing Rays，SBR）［5］、迭代物理光学法（Iterative Physical Optics，IPO）［6-8］、矩 量 法（Method of Moments，MoM）［9-10］等。SBR 和IPO 属于高频渐近方法，计算速度、快占用内存少，但是其计算精度低且不好控制。MoM 是一种基于频域电磁积分方程的准确数值方法，将积分方程离散成矩阵方程求解。对于内部具有复杂结构的发动机排气腔体，与高频渐近方法相比，MoM 可以给出更准确的结果［11］。但是传统的MoM 迭代求解方法的计算和存储复杂度很高，导致其难以计算电大排气腔体。多层快速多极子算法（Multilevel Fast Multipole Algorithm，MLFMA）［12］是MoM 的一种快速求解算法，可以显著降低MoM 的计算和存储复杂度，但是该算法并不改变基函数的数目，在计算电大腔体时仍然花费较多的计算时间和内存。特征基函数法（Characteristic Basis Function Method，CBFM）［13-15］可以显著降低基函数的数目，与MLFMA 相结合可以获得更高的计算效率并节省更多的计算内存［16-17］。

本文利用插值分解（Interpolative Decomposition，ID）［18-19］进 一 步 改 进CBFM-MLFMA 的计算效率，并将改进后的方法应用于航空发动机排气系统的电磁散射特性仿真中。插值分解可以将CBFM-MLFMA 中单站激励矩阵压缩分解成2 个小矩阵的乘积，因此CBFM-MLFMA 只需求解较少数的平面波激励，而其他平面波激励的解可以通过已求出解的插值得到，而不需要再进行耗时的迭代求解。 本文利用ID-CBFMMLFMA 对发动机排气系统的单站RCS 进行仿真计算，显著提高了计算效率，并与试验测试结果进行对比，验证了算法的精度。

1 排气系统电磁散射问题

研究发动机排气系统腔体电磁散射时，为了排除发动机排气腔体外表面散射的影响，常将发动机排气腔体安装在一个低散射载体中。图1 给出了一个典型的轴对称排气系统安装在一个低散射载体（见图2）中形成的电磁散射研究模型示意图，主要包括腔体内壁面、中心锥、火焰稳定器、支板、低散射载体等组成。涡轮叶片近似处理成金属平板。图3 为研究模型实物照片。

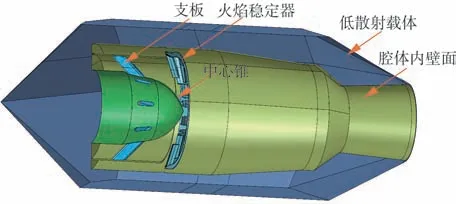
图1 轴对称排气系统与低散射载体示意图Fig.1 Schematic diagram of an axisymmetric exhaust system with a low scattering carrier

图2 低散射载体模型示意图Fig.2 Schematic diagram of a low scattering carrier

图3 轴对称排气系统的实物照片Fig.3 Photo of an axisymmetric exhaust system

为了建立求解发动机排气系统电磁散射的积分方程，将图1 所示的排气系统抽象成图4。其中，Sin表示腔体的内表面；Sout表示低散射载体的外表面，n表示腔体表面的单位外法向。Ei表示外来平面波的电场，Es表示腔体目标的散射电场。

图4 发动机排气系统电磁散射的示意图Fig.4 Schematic diagram of electromagnetic scattering from an engine exhaust system

根据等效原理对图4 中的腔体散射问题建立严格的电磁积分方程，得到电场积分方程（Electric Field Integral Equation，EFIE）和磁场积分方程（Magnetic Field Integral Equation，MFIE）如下：

式中：J(r)表示目标表面的感应电流；Hi表示外来平面波的磁场；Hs表示腔体目标的散射磁场。根据场源关系，Es(r)和Hs(r)可以表示为

其中：G(r，r′)表示自由空间的格林函数。可以发现，与SBR 和IPO 方法不同，方程（1）和（2）是严格的，没有近似，因此可以用于求解不同频率和不同入射波的电磁散射问题。

由于单独使用方程（1）或者方程（2）都会存在伪内谐振问题，这里使用混合场积分方程（Combined Field Integral Equation，CFIE），它是方程（1）和（2）的线性组合。

求解方程（5）可以得到腔体表面的感应电流J(r)，进而可以求出腔体的散射场Es(r)及其雷达散射截面RCS （σ）

2 计算方法

针对准确计算发动机排气系统电磁散射时间长的问题，本文利用一种并行的插值分解-特征基函数法-多层快速多极子算法（ID-CBFMMLFMA）对发动机排气系统的单站RCS 进行快速准确仿真。

2. 1 特征基函数法-多层快速多极子算法

利用矩量法（MoM）［9-10］可以将电磁散射积分方程转化成矩阵方程来求解。首先，利用RWG 基函数对感应电流进行展开

式 中：fn(r) 表 示 第n 个Rao-Wilton-Glisson（RWG）基函数［20］；In为待求的展开系数。然后，将式（7）代入CFIE，并利用Galerkin 检测，得到最终需求解的矩阵方程

式中：Z 和V 分别称为广义阻抗矩阵和广义电压矩阵。

CBFM 是一种宏基函数法，通过在较大区域上定义宏基函数，称之为特征基函数（CBF），可以实现未知量的缩减，从而降低阻抗矩阵所占内存，并减少阻抗矩阵方程的迭代求解时间。并且所构造的特征基函数具有激励无关（Excitation Independent，EI）的 特 性［13］，其 主 要 特 点是：CBF 只需要构造一次，就可以应用于不同极化和方向的平面波照射的散射问题，而不需要重复构造CBF，这种特性非常适合于单站RCS的计算。

在CBFM 中，首先要对目标进行分块，然后在每一块上构造出相应的特征基函数。CBF 的生成分为2 步，第1 步生成一组通过平面波照射得到的初始CBF；第2 步使用奇异值分解去除初始CBF 中的线性相关部分。通常，保留的CBF数目要远小于RWG 的数目［13-15］。

当所有块上的CBF 都生成好之后，可以用CBF 压缩传统MoM 的阻抗矩阵，得到缩减后的阻抗矩阵方程

式中：ZR表示利用CBF 压缩后的矩阵，称之为缩减 矩阵；VR是CBFM 中的电压 向量；α 为 待求的CBF 的线性表出系数。

式中：J 由各块保留的CBF 聚集而成。

图5 给出了用CBF 压缩MoM 阻抗矩阵的示意图，图中等号左边的蓝色小方块代表传统MoM 中阻抗矩阵的子矩阵，2 个细长的块对角矩阵表示CBF 矩阵，等号右边的橙色方块表示压缩后的阻抗矩阵的子矩阵。可以看出CBFM 可以显著降低内存需求，同时与之相关的矩阵向量积（Matrix Vector Product，MVP）的计算时间也会显著减少。

图5 CBFM 对MoM 阻抗矩阵的压缩Fig.5 Compression of MoM impedance matrix by using CBFM

为了进一步提高计算效率和降低内存需求，使 用 多 层 快 速 多 极 子 算 法（MLFMA）［11，15］对CBFM 进行加速。要使用MLFMA，需要将目标进行多层八叉树分组。基于组与组之间的相对位置关系，将CBFM 的缩减阻抗矩阵ZR分解为和两部分

利用加法定理，可以将CBFM 中与远场阻抗相关的MVP 转化成“聚集-转移-发散”的形式［16-17］，这样可以大大提高MVP 的计算效率。在此基础上，再利用多层分组、插值、反插值技术，MLFMA 可以将CBFM 的MVP 的计算和存储复杂度降低至O(NCBFlg NCBF)，这里NCBF为CBF 基函数的总数目。

与传统的MLFMA 相比，CBFM-MLFMA在MVP 计算时间和内存消耗方面也更具优势。如果CBFM 的基函数压缩率为，也就是说基函数数目变为原来的1 R。那么，在CBFM-MLFMA 中，聚集和发散函数耗费的内存和迭代时间会变为传统MLFMA 的1 R，近场阻抗矩阵耗费的内存和迭代时间会变成传统MLFMA 的1 R2。例如压缩率R=10，那么聚集和发散函数耗费的内存和MVP 时间会变为原来的10%，耗费的内存和MVP 时间会变成原来的1%，效果很可观。

2. 2 缩减激励矩阵的低秩压缩

CBFM 降低了基函数的数目，MLFMA 降低了迭代求解中MVP 的计算复杂度，但是当计算单站RCS 时，由于需要对多入射角进行迭代求解，而迭代求解时间正比于入射角个数，因此这导致计算时间仍然可能很长。当入射平面波采样过密的时候，激励矩阵往往存在低秩 特 性，可 以 利 用 低 秩 分 解 算 法［15，19，21］进 行 压缩 分 解［18，22-23］。这 里 利 用 基 于 选 主 元 的QR 分解对CBFM-MLFMA 中的激励矩阵进行压缩分解。

式中：Q 是酉矩阵；R 是上三角矩阵。利用误差门限ε 对R 进行截断，当R 中的第p 行的对角线元素满足以下条件

将R 中相应的行去掉。这里，rp表示R 对角线上的第p 个值。ε 通常取值为10-3～10-4。

假设R 矩阵最终只有k 个行被保留，那么VR可以近似表示为

式中：R11是上三角矩阵；；Q1是Q 的一个子矩阵；是VR的一个子矩阵。如图6 所示，就是VR的插值分解［16-17］。

图6 CBFM-MLFMA中单站激励矩阵的插值分解示意图Fig.6 Schematic diagram of interpolative decomposition of monostatic excitation matrix in CBFMMLFMA

因此，只需要利用CBFM-MLFMA 求解下面的矩阵方程

则最终需要的解可以表示为可以看出，利用插值分解只需要求解k 次矩阵方程，因此计算效率得到提高。

2. 3 并行加速计算

为了充分利用CPU 的计算资源，利用共享内存的OpenMP 技术将ID-CBFM-MLFMA 程序进行并行。将ID-CBFM-MLFMA 算法中的4 个主要步骤进行并行：① 特征基函数的生成；② 聚集和发散函数的生成；③ 近场缩减矩阵的生成；④ 迭代求解时的MVP。

在特征基函数的生成步骤，需要对每组进行CBF 构造。由于每组CBF 的构造互不相关，因此非常适合并行。按组对CBF 构造进行并行，每个线程不存在竞争，可以获得很高的并行效率。与CBF 构造步骤相类似，聚集和发散函数的生成以及近场缩减矩阵的生成也是组与组之间互不相关的，非常适合并行，这里仍然是按组进行并行。在MVP 步骤，由于MLFMA 算法结构复杂，并行起来较为复杂。这里使用按组和按平面波2 种并行方式相结合的方式进行并行实现。

3 仿真结果与试验验证

试验件的结构图如图1 所示，而实物图如图3所示。该试验件为纯金属结构，放置在微波暗室中。RCS 测试系统的示意如图7 所示，包含天线、泡沫转台等。测量时方位角取值从-180°～180°，采样间隔为0.2°，共1 801 个角度。

图7 RCS 测试系统示意图Fig.7 Schematic diagram of an RCS test system

利用并行ID-CBFM-MLFMA 对轴对称排气系统的单站RCS 进行仿真计算，并与试验测试结果进行比较以验证算法精度。仿真模型的结构如图1 所示，是带有低散射载体的排气系统。网格剖分尺寸为0.1 波长。本文计算的单站RCS 均为VV 极化。仿真时方位角取值从-180°～180°，采样间隔为1°，共361 个角度。

3. 1 计算精度

首先，考虑轴对称排气系统在0°俯仰角的时候，在多个频率下的单站RCS。图8～图10 分别给 出 了 ID-CBFM-MLFMA、传 统 CBFMMLFMA 对轴对称排气腔体试验件在6 GHz、10 GHz、35 GHz 频率下，单站RCS 随方位角的变化进行仿真计算。 可以看出ID-CBFMMLFMA 的仿真结果与传统CBFM-MLFMA 的仿真结果几乎完全重合，ID-CBFM-MLFMA 的仿真结果和试验测试结果吻合良好。

图8 6 GHz 频率下VV 极化单站RCS 随方位角的变化Fig.8 VV-polarized monostatic RCS versus azimuth angle at 6 GHz

图9 10 GHz 频率下VV 极化单站RCS 随方位角的变化Fig.9 VV-polarized monostatic RCS versus azimuth angle at 10 GHz

图10 35 GHz频率下VV 极化单站RCS 随方位角的变化Fig.10 VV-polarized monostatic RCS versus azimuth angle at 35 GHz

图11 对比了35 GHz 频率下载体以及排气系统（含载体）的单站RCS。可以看出，在0°方位角附近角域，载体的单站RCS 远小于整体目标的单站RCS。因此，在这些角域可以认为整体目标的单站RCS 主要是由排气腔体贡献的。

图11 35 GHz频率下VV极化载体与排气系统的单站RCS对比Fig.11 VV-polarized monostatic RCS comparison of exhaust system and carrier at 35 GHz

3. 2 计算效率

接下来将ID-CBFM-MLFMA 与传统的CBFM-MLFMA 进行比较来说明ID-CBFMMLFMA 的计算效率。所使用的计算机配置是Intel （R） Core （TM） i9-10900K CPU，主 频3.7 GHz，10 核20 线程，总内存128 GB。并行线程数均设置为20。GMRES 收敛迭代收敛精度设置为0.001。使用了块对角预处理器。计算的是轴对称排气系统10 GHz 频率下VV 极化单站RCS。仿真时方位角取值从-180°～180°，采样间隔为1°，共361 个角度。插值分解的截断门限设置为0.001。

使用插值分解对激励矩阵进行压缩，得到有效秩为75。这意味着借助于插值分解，可以将迭代求解矩阵方程的次数减少到75 次，而传统的CBFM-MLMFA 则需要迭代求解矩阵方程361 次，因此ID-CBFM-MLFMA 可以显著降低迭代求解的时间，这对于计算发动机排气腔体的宽角RCS 特性很有帮助。表1 给出了2 种方法计算时间的比较，可以看出，与CBFMMLFMA 相 比，ID-CBFM-MLFMA 在 计 算CBF、近场缩减矩阵、聚集转移发散函数时耗费的时间相同，但是显著降低了迭代求解时的时间。

表1 计算10 GHz频率下VV 极化RCS的计算时间的比较Table 1 Comparison of calculation time for VVpolarized RCS at 10 GHz

4 结 论

本文将并行的ID-CBFM-MLFMA 算法应用于航空发动机排气腔体的电磁散射特性的仿真计算，并与试验测试结果进行对比验证。

1）与试验测试结果对比表明ID-CBFMMLFMA 具有良好的计算精度。和传统CBFMMLFMA 方法的精度几乎相同。

2）在计算航空发动机排气系统模型多角度单站RCS 时，与传统的CBFM-MLFMA 相比，ID-CBFM-MLFMA 具有更高的计算效率。在本文的算例中，迭代求解时间减少了78%。

3）理论上，并行ID-CBFM-MLFMA 是一种通用的算法，也可用于飞行器整机、发动机进气道等各种目标电磁散射特性的快速准确仿真。