大型CFRP 薄壁管桁架加劲环稳定性研究
米翔,陈务军,*,张祎贝,李世平,黄晓惠
1.上海交通大学 空间结构研究中心,上海 200240
2.新誉集团有限公司,常州 213166
平流层飞艇是现代航空器的重要分支,其凭借自身与大气间的密度差产生浮力,可实现在高度17~22 km 的平流层临近空间定点悬停或低速飞行[1]。按照结构形式分类,可以分为软式、硬式和半硬式3 种[2]。在硬式和半硬式飞艇中,桁架结构因为其结构形式简单、荷载分配合理等特点被广泛的应用[3-6]。高性能碳纤维复合材料(Carbon Fiber Reinforced Polymer,CFRP)因为具有轻质高强(比强度和比模量高)、耐湿性能、耐疲劳性能和耐磨性好等综合优异特点,逐渐代替以往桁架结构常用的铝合金、钛合金等金属材料,可以有效地减轻飞艇的结构质量,也是当今航天新材料的重点研究方向之一[7-11]。
相较于传统材料,复合材料桁架的理论研究和实际应用较少,关于其稳定性能与承载力性能的分析方法还处于发展阶段。Zhu 等[12]对的拉挤纤维增强复合材料(PFRP)桁架梁进行了压弯屈曲试验,并采用多种有限元模型进行仿真,可以较好地模拟结构的力学行为。Asay[13]采用线单元对IsoBeam 结构进行4 点弯曲仿真并通过构件试验确定仿真参数,发现仿真模型能够预测桁架失效模式。Woods 等[14]采用直接刚度法对缠绕整体成型复合材料桁架进行了弯曲和扭转仿真,相应测试结果表明仿真模型能较好地给出结构刚度和强度。Pfeil等[15]对组装式复合材料桁架桥进行了抗弯试验,揭示了CFRP 桁架结构的弯曲失效模式。鞠苏[16]研究了轻质纤维增强复合材料三角桁架在非线性结构响应约束下的多参数优化方法。南波[17]对平流层飞艇复合材料骨架的CFRP 管的稳定性、桁架节点的极限承载能力、桁架的抗弯扭性能以及骨架的轻量化设计等问题开展了系统研究。熊波[4]建立了疏密网格结合的仿真模型,兼顾仿真效率与精度,能较好地模拟全复合材料桁架的弯曲、扭转和振动试验。然而上述研究所涉及的结构尺度均较小,且较少有文献对复合材料桁架结构的稳定性能做系统的研究。
本文所涉及的半硬式飞艇创新性地采用轻质高刚性索桁张拉结构作为飞艇的关键结构部件,因其结构类似于自行车车轮,故也被称为轮辐式张拉结构[18],本文称之为加劲环。由于其外形呈圆形,结构简单,特别适用于飞艇。轮辐结构在大跨空间结构中被广泛使用[19-20],而且大多巨型柔性摩天轮也采用此种结构[21-22]。建筑结构中,关于轮辐式张拉结构的稳定性研究较多,但过于保守,仅考虑张拉荷载,未考虑径向拉索对于结构稳定性能的提升作用,且材料、桁架构型和节点、制造、张拉、工况等不同,所以本文对此进行全面的稳定分析是有必要的。
本文针对某半硬式平流层飞艇的关键部件-轮辐式张拉结构的CFRP 加劲环,利用ABAQUS 建模,考虑其预张拉过程,首先进行特征值屈曲分析,在此基础上考虑初始几何缺陷、预应力等因素进行非线性稳定分析,最后经过大量计算研究了初始几何缺陷分布形式及其幅值大小对结构稳定的影响规律。
1 结构概述
1. 1 飞艇结构
典型的半硬式飞艇结构主要由外囊体、龙骨和内气囊3 部分组成,其中飞艇龙骨是最主要的承重结构。根据总体设计任务的要求,本文涉及的飞艇采用一种自平衡的张拉整体结构作为飞艇龙骨,结构长150 m,直径40 m,由7 个加劲环、7 个中芯桁架和纵向拉杆组成,见图1。在完成结构总装后,龙骨成为一个张拉整体,中芯桁架和加劲环受压,而径向拉杆受拉。龙骨主要采用CFRP 制造,与外囊体形成“皮包骨”的刚柔一体结构体系,能以较少的材料提供较高的刚度,极大减轻结构质量,同时2 个层次的结构更具有体系性、冗余性和较强的抗损性与鲁棒性。为了适应飞艇的外部轮廓,加劲环2~6 具有相同的几何结构,横截面对称;而加劲环1 和加劲环7 的横截面不对称,制造和集成工艺及受力更复杂,因此其首先被用于制造和集成的方法验证,并以加劲环7 作为研究对象。

图1 飞艇龙骨布局图Fig. 1 Layout diagram of airship keel
1. 2 加劲环组成
加劲环为典型的预应力轮辐式索桁结构,主要由外环桁架、径向拉杆、中心毂轴3 部分组成,见图2 所示。外环桁架直径为21.3 m,桁架截面为边长500 mm 的正三角形,具有34°的旋转角度,桁架由28 个标准节段装配而成,节段之间用三角形端板连接。标准节段由3 根弧形的弦杆(∅35 mm×0.5 mm)和18 根腹杆(∅20 mm×0.5 mm)构成,全部由碳纤维复合材料制备,特殊的拓扑设计实现规格化、简洁的节点:单K 和双K 铝合金三维整体节点。径向拉杆采用低松弛高刚性CFRP 拉杆替代非线性强、模量低、易松弛拉索,上下各28 根,直径4 mm,张拉平衡状态上径向拉索设计长度为10.484 m,下径向拉索设计长度为10.179 m。中心毂轴外径150 mm,壁厚为1.5 mm,内部填充有聚甲基丙烯酰亚胺泡沫材料,毂轴长度为2 150 mm。
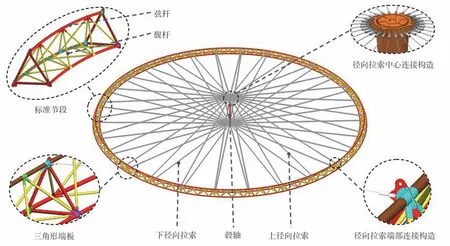
图2 加劲环结构组成示意图Fig. 2 Diagram of stiffening ring structure composition
1. 3 加劲环装配
根据公开报道的资料,尚未发现如此大尺寸CFRP 桁架结构的应用案例,所以对其装配任务提出了巨大的挑战。结构为预应力张拉结构,其力学性能高度依赖于径向拉索的张拉状态,所以对装配精度要求较高。加劲环的组装过程首先是外环桁架的装配,由28 个节段拼装而成,并支撑于16 个环形分布的铝合金支架上,见图3。随后进行毂轴的定位,为保证径向拉索内力的均匀性,精确定位至关重要。完成定位之后将径向拉索一端连接于外环桁架,一端连接于中心毂盘及顶推装置,通过电机推动将索力张拉到设计张拉值,由于制造和装配误差的存在,该过程需要反复迭代多次才能张拉至设计值。最后,将径向拉索张拉端固定在毂轴端部,并拆去顶推装置,结构成型,成为一个自平衡的预应力张拉结构。

图3 加劲环装配Fig. 3 Stiffening ring assembly
2 稳定分析方法
2. 1 特征值屈曲分析
特征值屈曲分析是非线性稳定分析的基础。不考虑非线性和初始缺陷因素,可预测结构的线性屈曲荷载,作为屈曲荷载值的上限,为非线性屈曲分析提供参考,且其屈曲模态可作为初始几何缺陷的分布形式。通过平衡法或能量法可以推导出特征值屈曲分析的特征方程[23]:
式中:KE为结构的线弹性刚度矩阵;KG为初应力刚度矩阵或几何刚度矩阵;λ 为特征值,也即荷载因子;ϕ 为特征值位移向量,也即屈曲模态。
子空间迭代法(Subspace iteration)和Block Lanczos 是2 种典型的特征值屈曲分析方法,本文采用第2 种方法进行计算。
2. 2 非线性屈曲分析
采用弧长法对结构进行全过程的非线性跟踪分析,可以得到荷载-位移曲线的下降曲线。假定采用比例加载,荷载为保守荷载,则结构非线性稳定分析增量方程为[24]
式(2)中有未知数Δu 及Δλ 共N+1 个,但只有N 个平衡方程,故需补充1 个约束方程:
式中:Δli为弧长;β2为比例因子,由它调节载荷增量和位移增量在弧长Δli中的作用,它对弧长法的总体性能有很大影响。
3 特征值屈曲分析
利用ABAQUS 进行建模分析。在加劲环的预张拉阶段,毂轴不参与受力,所以对毂轴不建模。外环桁架中的弦杆、腹杆及拉索均用三维两节点线性梁单元(B31)建模,节点作刚接处理,约束下索中心连接点Ob的3 个平动自由度,并在上索中心连接点Ou施加单位集中力F 进行特征值屈曲分析,见图4。外环桁架薄壁管采用T700S2预浸料,厚度0.08 mm,铺层设计为[+45°/0°/0°/0°/0°/-45°],经过测定管的整体承压弹性模量取7×104MPa,密度为1 785 kg/m³,径向拉索弹性模量取2×105MPa,密度为7 850 kg/m³,二者的泊松比均为0.3。
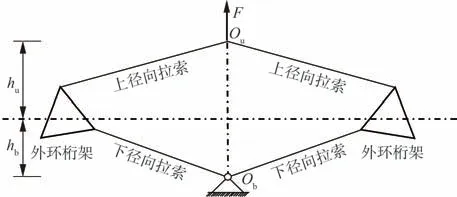
图4 结构加载示意简图Fig. 4 Structure loading schematic diagram
为了得到结构整体的屈曲模态,提取了前150 阶模态。由于结构对称,屈曲模态成对出现,图5 给出了结构前3 阶局部屈曲模态(第1、2、4 阶)和前3 阶整体屈曲模态(第87、116、124阶),最大位移均值均为1,对应的特征值分别为7 131.4、7 141.9、7 173.5 和13 169、14 257、14 420,由此可以看出结构首先发生局部屈曲,其特征值较为密集,且相对于整体屈曲,特征值较小。这里的局部屈曲是指结构局部节点发生较大位移,而整体屈曲是指桁架整体发生明显的弯曲,呈波浪状。将第1 阶特征值屈曲荷载施加到结构上再进行静力分析,得到上、下径向拉索应力分别为155 MPa、186 MPa,较之于50 kg和65 kg 的设计拉力水平,有接近4 倍的安全余量。
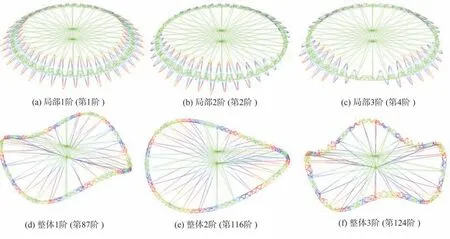
图5 前3 阶局部屈曲模态与前3 阶整体屈曲模态Fig. 5 First three local buckling modes and first three global buckling modes
在加劲环的预张拉阶段,上径向拉索向上张拉,下径向拉索向下张拉,结构的几何构型一直处于变化的过程,而在这个过程中径向拉索一方面作为结构本身,能起到提高结构稳定性能的作用,而另一方面,对于外环桁架径向拉索则是作为一种外荷载存在,所以过大的索力反而导致结构失稳。因此,存在最优索力实现最高刚度和稳定。为了研究张拉过程的稳定性,进行不同张拉状态下结构特征值屈曲分析。数值分析为2 步,首先考虑重力荷载下将上径向拉索中心点Ou张拉提升到一定位移,然后进行特征值屈曲分析。
图6 给出了从初始构型以50 mm 的增量张拉到800 mm 的过程中,结构前3 阶局部屈曲和前3 阶整体屈曲的临界荷载的变化曲线。由图可知,前3 阶局部屈曲的屈曲荷载随着张拉位移的增大而减小,而前3 阶整体屈曲的临界荷载随着张拉位移先增大后减小。张拉过程可以视为施加径向拉索预应力的过程,此时作为荷载,外环桁架局部屈曲的屈曲荷载下降;而作为整体结构来看,张拉位移的增大导致径向拉索水平投影角度增大,水平分力减小,竖向分力增大,且水平投影角度的增大能有效提升径向拉索防止外环桁架发生整体面外失稳的能力,从而结构发生面外失稳则需要更大的索力,再到后期,结构预应力也越来越大,二者综合起来看,整体屈曲特征值便有先增大后减小的趋势,故从整体稳定的角度来看,张拉位移存在一个最优值。
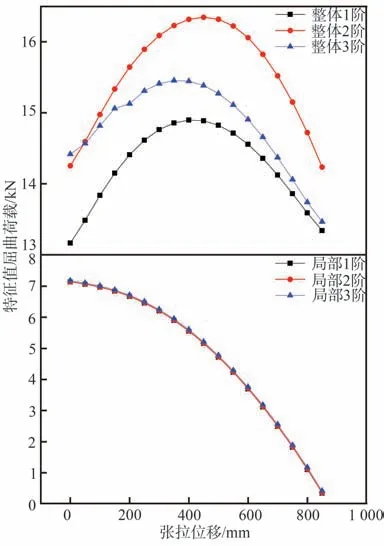
图6 不同张拉位移下的屈曲荷载Fig. 6 Buckling loads with different tension displacements
4 非线性屈曲分析
4. 1 预张拉工况的几何非线性屈曲分析
考虑加劲环的预张拉过程,在上径向索中心点Ou施加单位位移荷载,采用弧长法进行全过程的非线性稳定分析。计算发现如果采用一致缺陷模态法,发现第1 阶屈曲模态作为初始几何缺陷得到的临界屈曲荷载并非最小,所以分别将前3 阶局部屈曲模态和前3 阶整体屈曲模态作为初始几何缺陷。参考结构尺寸与装配精度,前者的最大缺陷值取2 mm,后者的最大缺陷幅值取40 mm。
计算得到外环桁架位移最大点的荷载-位移曲线如图7 所示(荷载为下径向索中心点Ob的支座反力)。由图可知,未考虑初始几何缺陷的理想模型的临界屈曲荷载为14.381 kN,而考虑初始几何缺陷后的临界屈曲荷载大幅降低,局部屈曲模态作为缺陷时,局部2 阶最小,为9.36 kN,减小34.91%;整体屈曲模态作为缺陷时,整体1 阶最小,为8.21 kN,减小42.91%。此外,可以看到结构对于初始几何缺陷非常敏感,不同的屈曲模态作为初始几何缺陷作为缺陷,曲线的后屈曲阶段完全不同,最终的非线性屈曲模态也不同。
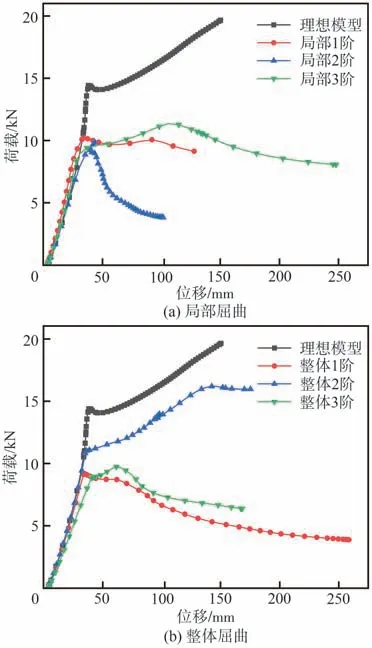
图7 预张拉工况的荷载-位移曲线Fig. 7 Load-displacement curves under pre-tension
4. 2 定毂轴长度下的几何非线性屈曲分析
4.2.1 初始构型的稳定分析
“降温法”是利用物体的热胀冷缩特性,对径向拉索进行降温使之收缩,从而使得径向拉索受拉,外环桁架受压,能有效施加结构的预应力。为了考虑初始预应力,即拉索的张拉状态对于结构稳定性能的影响,这里在初始构型下给径向拉索施加不同的初始预应力(综合考虑设计水平与径向拉索强度值确定取值范围),同时考虑重力荷载先进行一次非线性分析,平衡后再利用“降温法”,给径向拉索施加单位温度荷载,同样采用弧长法进行非线性稳定分析。结合4.1 节的计算结果,这里分别以局部2 阶和整体1 阶屈曲模态作为初始几何缺陷。得到荷载比例因子(Load Proportion Factor, LPF)-位移曲线见图8 所示,从图中可以看到,随着初始预应力的增大,曲线整体的变化趋势不变,临界屈曲荷载因子不断减小。
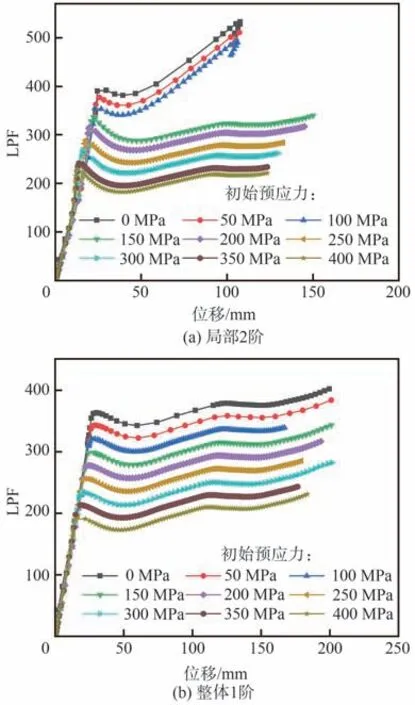
图8 不同初始预应力下的LPF-位移曲线Fig. 8 LPF-displacement curves under different initial prestress
图9给出了不同初始预应力下结构屈曲时上下径向拉索的最大应力和临界屈曲荷载因子的变化曲线,从图中可以看到,临界屈曲荷载因子随初始预应力的增大呈线性减小,而屈曲时索的最大应力几乎保持不变,且上索应力小于下索应力。对于局部2 阶的缺陷模式,上、下索的最大应力平均值分别为214 MPa、314 MPa,对于整体1 阶的缺陷模式,上、下索的最大应力平均值分别为245 MPa、331 MPa。
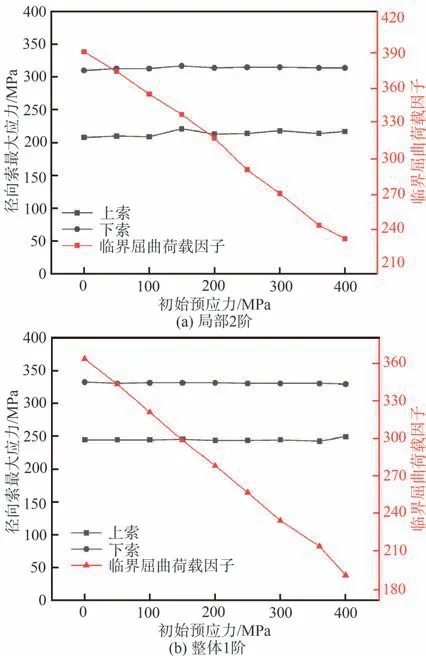
图9 不同初始预应力下索最大应力与临界屈曲荷载因子Fig. 9 Maximum stress and critical buckling load factor of cable under different initial prestress
4.2.2 张拉后构型的稳定分析
同样考虑到加劲环的预张拉过程,在将上径向索中心点Ou分多级向上张拉一定位移之后,再利用温度荷载进行非线性稳定分析。图10 给出了2 种缺陷模式下,分别张拉200、400、600、800 mm 的位移之后进行非线性稳定分析的结果(LPF-位移曲线)。从图中可以看到,在经过张拉之后结构的临界屈曲荷载因子明显下降。
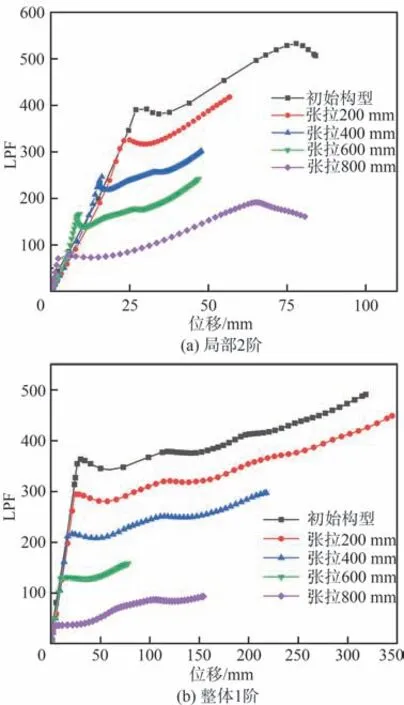
图10 不同张拉位移下的LPF-位移曲线Fig. 10 LPF-displacement curves with different tension displacements
图11给出了不同张拉位移下,结构临界屈曲荷载因子与上下索最大应力的变化曲线,从图中可见,临界屈曲荷载因子随着张拉位移的增大呈线性减小,而上径向拉索的最大应力增大,下径向拉索的最大应力减小,逐步趋于一致。关于此结果,张拉位移的增大使得径向索的应力不断增大,相当于给索施加预应力,从而导致计算结果与4.2.1 中的计算结果类似。此外,径向拉索最大应力的变化,是由于上下径向拉索在竖向的高度(图3 中的hu与hb)变化导致,如果径向拉索上下对称,二者的力应该完全一致,在向上张拉的过程中,由于二者长度的变化程度不一致,导致其高度之比一直在变化。图12 给出了上下径向拉索高度之比与最大应力之比的变化趋势,可以看到二者是相关的,变化趋势一致。
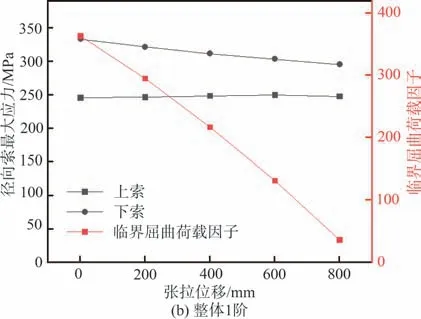
图11 不同张拉位移下索的最大应力与临界屈曲荷载因子Fig. 11 Maximum stress of cable and critical buckling load factor with different tension displacements
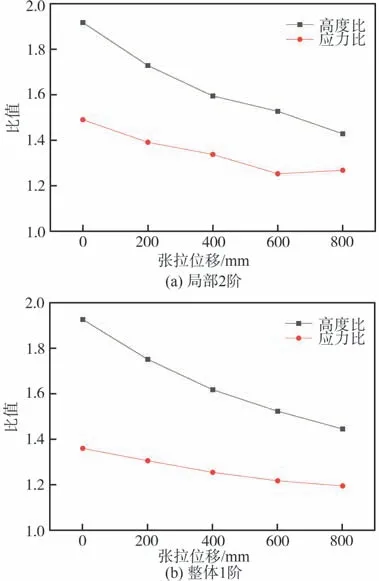
图12 不同张拉位移下索的高度比与最大应力比Fig. 12 Height ratio and maximum stress ratio of cable with different tension displacement
此外在不同的张拉位移下,同时考虑初始预应力的影响,图13 给出了在初始构型、张拉200 mm 和张拉400 mm 的构型下,分别考虑0、100、200、300、400 MPa 的初始预应力后,2 种缺陷模式下结构临界屈曲荷载因子的变化曲线。同样发现在不同的张拉位移之下,结构的临界屈曲荷载因子依旧随着初始预应力的增大而线性减小。
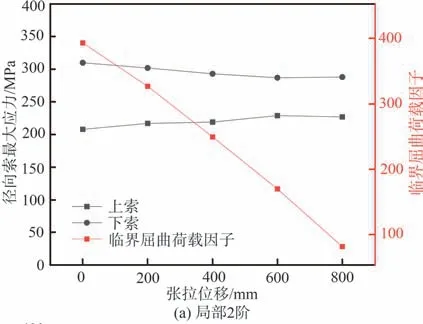
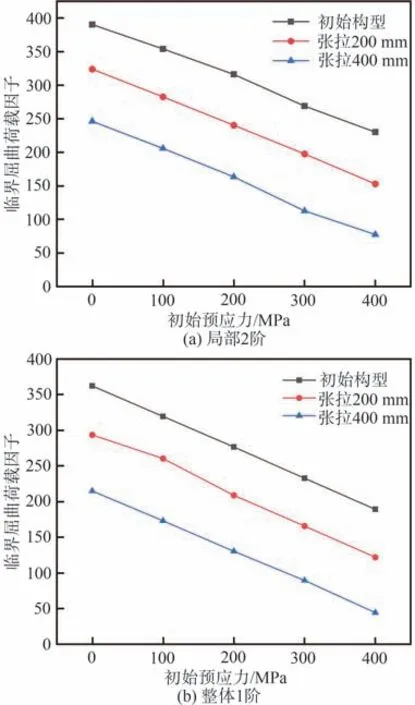
图13 各级张拉构型和初始预应力下的临界屈曲荷载因子Fig. 13 Critical buckling load factor of different initial prestress with different tension configurations
最后,为了对4.1 节和4.2 节中的2 种计算方法的计算结果有所对比,取2 种缺陷模式的结构在张拉800 mm 后的屈曲时径向索的最大应力,与4.1 节中的计算结果进行对比,见表1。可以发现结果十分接近,这表明2 种形式的分析方法最终得到的结果一致,足以见得分析方法是有效可行的。

表1 屈曲时径向索的最大应力对比Table 1 Comparison of maximum stress of radial cable under buckling MPa
4. 3 初始几何缺陷分析
由4.1 节的计算结果可以看到,结构稳定性能对于初始几何缺陷的模式非常敏感,故此处采用修正的一致缺陷模态法,首先分别以前3 阶局部屈曲模态和前3 阶整体屈曲模态作为初始几何缺陷的形式,同时考虑不同大小的缺陷幅值进行缺陷分析;然后考虑利用此6 阶屈曲模态的组合作为初始几何缺陷。
4.3.1 单一模态缺陷分析
结构初始几何缺陷幅值参考标准节段的制造精度和加劲环的装配精度,前3 阶局部屈曲模态作为初始几何缺陷时,分别考虑0.5、1、2、3、4、5 mm 的幅值大小,若设节段节距为l,则分别约 为 l/4 600,l/2 300,l/1 150,l/770,l/575,l/460;而前3 阶整体屈曲模态作为初始几何缺陷时,分别考虑30、40、50、60 mm 的幅值大小,若设加劲环最大直径为L,则分别约为L/700,L/530,L/430,L/350。计算结 果 见 图14 所示,从图中可以发现,当缺陷形式为局部1 阶和局部3 阶时,随着缺陷幅值的增大,曲线的后屈曲阶段会有明显变化,因为幅值越小,结构越接近理想模型。
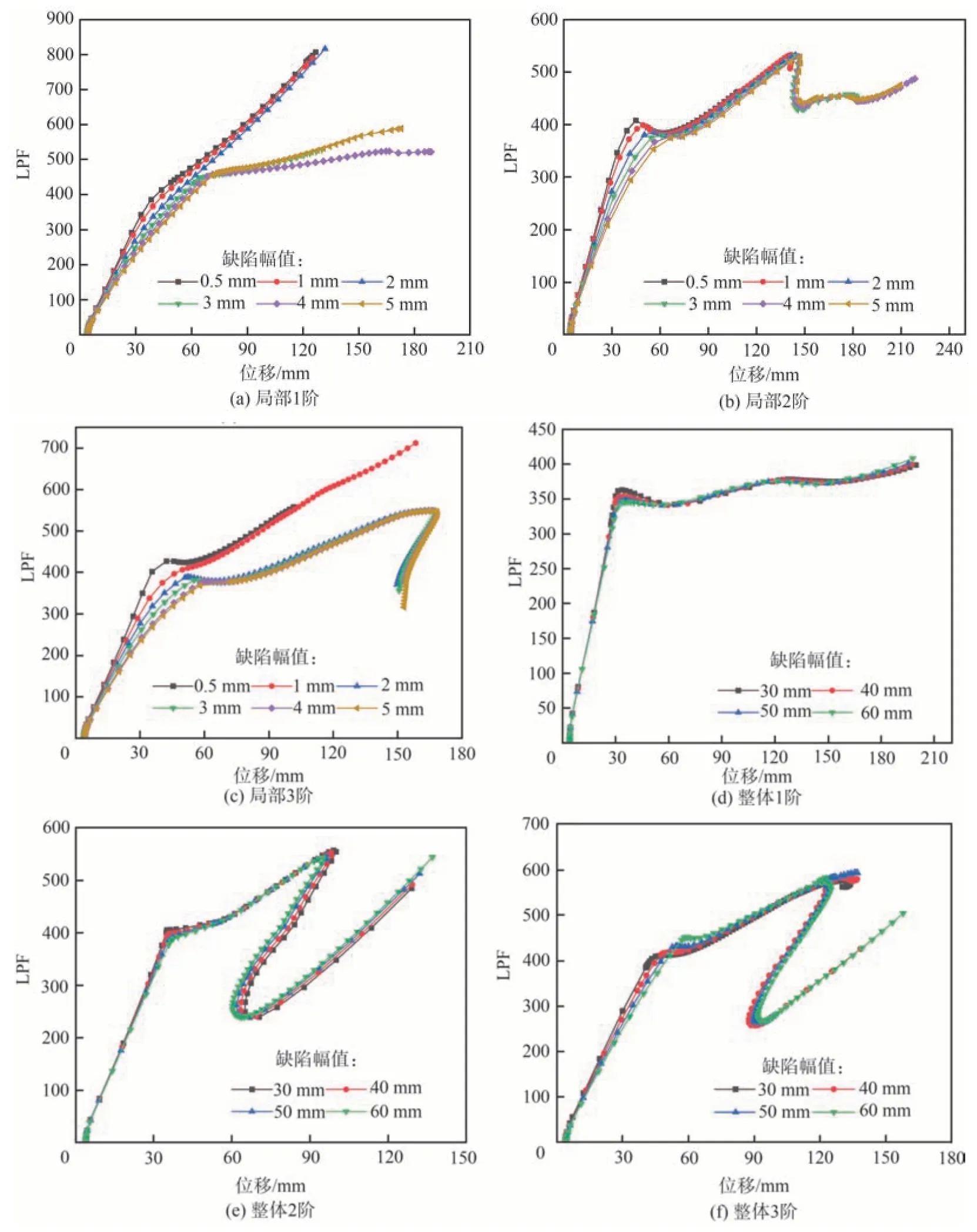
图14 不同缺陷幅值下的LPF-位移曲线Fig. 14 LPF-displacement curves with different imperfection amplitudes
图15给出了临界屈曲荷载因子随缺陷幅值的变化曲线,从图中可以看到,当缺陷分布形式为局部1 阶和整体3 阶时,临界荷载因子随缺陷幅值的增大而增大,其他缺陷形式下临界屈曲荷载因子随缺陷幅值的增大而减小。而且从图中可以很直观地看到,局部1 阶屈曲模态并非结构的最不利缺陷分布形式,并且其临界荷载值相对较大,而局部2 阶和局部3 阶屈曲模态的缺陷形式得到的临界屈曲荷载因子相差不大;整体1 阶屈曲模态为结构的最不利缺陷分布形式,得到的临界屈曲荷载因子最小。
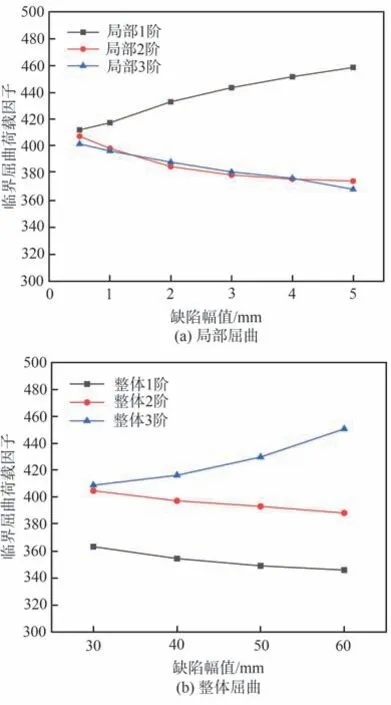
图15 缺陷幅值对临界屈曲荷载因子的影响Fig. 15 Effect of imperfection amplitude on critical buckling load factor
此外,发现径向拉索内力的大小跟几何缺陷分布形式十分相关,不同的几何缺陷形式导致不同的拉索内力分布形式。图16 给出了不同的几何缺陷分布形式下,屈曲时径向拉索的内力分布与大小。从图中可以看到,局部屈曲模态做初始几何缺陷时,径向拉索的内力分布较为均匀,但仍具备一定规律性;而整体屈曲模态作为初始几何缺陷时,径向拉索的内力分布十分不均匀,变化较为明显。由此可见,径向拉索内力的分布与几何缺陷形式紧密相关,而且都是呈对称分布的。
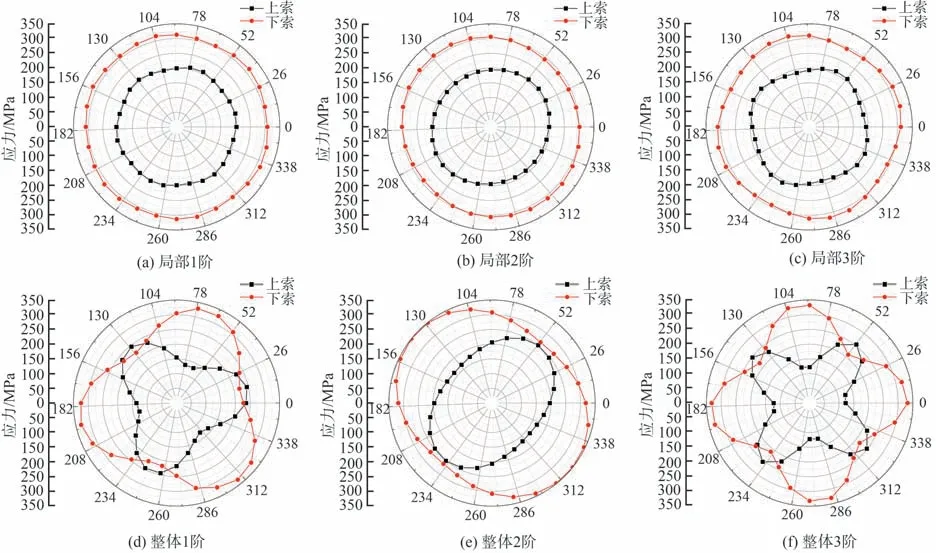
图16 结构屈曲时径向拉索的应力Fig. 16 Stress of radial cable during structural buckling
4.3.2 多模态组合缺陷分析
由于制造偏差、装配误差等因素,实际的几何缺陷是随机的、复杂的,如果简单地只用某一阶屈曲模态来假设初始几何缺陷是不安全的,所以考虑利用多阶屈曲模态的组合作为初始几何缺陷的分布形式。一般利用式(4)来考虑多模态的组合[25-26]。
式中:f0为初始几何缺陷场,ϕi为第i 阶特征值屈曲模态,通常其最大值被归一化为1;αi为参与模态的幅值系数;ci为各阶模态的参与系数;N 为参数模态的总阶数。
表2 给出了所有组合,这里参与系数ci均为1,改变幅值系数αi,利用不同的模态进行组合。

表2 多模态组合缺陷的幅值αiTable 2 Amplitude αi of multi-mode combined imperfection
图17 将单模态缺陷和多模态缺陷组合的临界屈曲荷载因子作对比,易见得,相比于单一模态缺陷,多模态组合缺陷的临界屈曲荷载因子更小。单一模态缺陷的临界屈曲荷载因子区间为[346,458],而多模态组合缺陷的临界屈曲荷载因子区间为[305,367],所以多模态组合缺陷更能反映结构的真实几何缺陷;相比于组合1~15,组合16~23 的临界荷载明显变小,同时考虑局部屈曲模态和整体屈曲模态的多阶屈曲模态的组合更能反应结构真实的初始几何缺陷;综合比较所有组合,发现当全部3 阶局部屈曲模态和3 阶整体屈曲模态均参与时,结构的临界荷载因子最小。
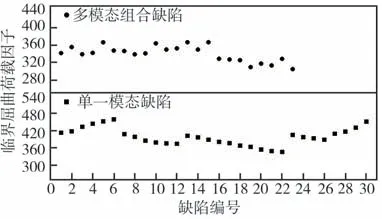
图17 单一模态缺陷与多模态组合缺陷结果对比Fig. 17 Comparison of results of single-mode imperfection and multi-mode combined imperfection
5 结 论
本文对某半硬式平流层飞艇的关键结构部件-大型CFRP 薄壁管桁架加劲环进行了稳定性能分析研究,主要得到以下结论:
1)结构首先发生局部屈曲,且相对于整体屈曲,特征值较小;随着张拉位移的增加,前3 阶局部屈曲特征值减小,而前3 阶整体屈曲特征值先增大后减小,存在最优张拉值。
2)对于预张拉工况,考虑整体1 阶模态的初始几何缺陷使得结构临界屈曲荷载下降42.91%,且结构后屈曲路径对初始几何缺陷十分敏感。对于定毂轴长度的工况,结构临界屈曲荷载因子随着初始预应力的增大和张拉位移的增加均呈线性减小;随初始预应力的增大,上下索最大应力几乎保持不变;而随张拉位移的增加上索最大应力增大,下索最大应力减小,但其比值的变化趋势与上下索高度的比值变化趋势一致。
3)局部1 阶并非结构最不利缺陷形式,当整体1 阶屈曲模态作为初始几何缺陷时,临界屈曲荷载因子最小。屈曲时的索力分布与几何缺陷形式紧密相关。多模态组合缺陷更能反映结构真实几何缺陷,得到的临界屈曲荷载因子明显小于单模态缺陷。

