基于多源信息的隐含非线性维纳退化过程剩余寿命预测
杨家鑫,唐圣金,*,李良,孙晓艳,祁帅,司小胜
1.火箭军工程大学 导弹工程学院,西安 710025
2.火箭军工程大学 作战保障学院,西安 710025
3.火箭军装备部驻郑州军代表室, 郑州 450000
在工程应用中,设备的性能会随着时间累积呈现一种缓变的退化趋势[1],当其退化水平超过失效阈值时,可能会导致设备停机,甚至引发事故。剩余寿命是指设备在当前时刻距离失效时刻的时间长度[2],准确的剩余寿命预测有助于操作人员在设备接近失效前做出正确的维护决策,从而有效提高设备的可靠性安全性,并降低设备的经济成本[3-5]。近年来,随着航空航天、军事等高可靠性领域的快速发展,统计数据驱动的剩余寿命预测方法已经成为可靠性领域研究的热门问题[6-7]。
统计数据驱动的剩余寿命预测可以充分利用同类设备的状态监测数据[8]。其基本原理:根据历史退化数据或失效寿命数据估计表示退化过程共性特征的未知参数;然后根据实时检测的现场退化数据在线更新漂移参数;最后利用剩余寿命的概率密度函数(Probability Density Function,PDF)预测剩余寿命。由于设备的退化过程具有随机性,因此剩余寿命预测经常使用随机过程建模[9],基于随机过程的剩余寿命预测方法具有物理解释清晰、数学性质好等优点[10]。Gebraeel 等[11]首次提出通过贝叶斯方法将现场退化信息与先验退化信息合理融合,并利用得到的后验信息进行剩余寿命预测。该方法开始主要应用于随机系数回归模型[11-13],之后,被推广到了伽马过程[14]、逆高斯过程[15]、基本维纳过程[16]等随机过程退化模型。值得注意的是,因维纳退化过程模型同时适用于单调和非单调的退化系统,近些年已被广泛使用[17-18]。然而,在工程应用中,具有非线性特征的退化系统广泛存在,基本线性退化模型难以有效跟踪非线性退化过程[19-20],可能会导致剩余寿命预测精度偏低。此外,在工程应用中,经常会遇到不完美或缺失的先验退化信息,这可能会导致先验参数估计不准确或无法估计出先验参数[13],进而导致剩余寿命预测精度降低甚至失败[9,21]。针对先验退化信息不完美或缺失的问题,现有的文献主要有2 种解决方法。
第1 种方法是结合期望最大化算法(Expectation Maximization,EM)和贝叶斯方法。该方法最早由Wang 等[22]提出,用于拟合带有漂移参数的自适应布朗运动模型。然后,Si 等[21]基于线性维纳退化过程模型采用贝叶斯更新方法和EM算法对模型参数和剩余寿命分布进行更新,并推导了一个精确封闭的剩余寿命分布函数。然后,该机制被扩展到了隐含线性维纳退化过程[23]、非线性维纳退化过程[24-25]和隐含非线性维纳退化过程[26]。联合EM 算法和贝叶斯方法可以克服先验信息不完美和缺失对剩余寿命预测结果的影响。Tang 等[27]通过假设模型漂移参数固定,推导了隐含线性维纳退化过程模型的参数解析表达式,证明了该联合算法与传统极大似然估计(Maximum Likelihood Estimation, MLE)方 法具有相同估计结果的结论。然而,为什么该方法能够获得比传统的贝叶斯方法更好的预测结果的机理仍有待进一步深入研究。
第2 种方法是融合多源信息方法。通常,用于退化模型参数估计的数据有3 种:同类设备的历史退化数据(包括加速退化数据[28])、同类设备的失效寿命数据和被评估设备的现场退化数据,如何利用这3 种数据所包含的多源退化信息进行剩余寿命预测称为融合多源信息的剩余寿命预测方法。Tang 等[29]基于线性维纳过程模型得到了参数估计结果与退化数据特征之间的关系,为合理融合多源信息提供了理论依据。然而,在实际应用中,特别是对于一些新设备,可能缺乏足够的失效寿命数据或历史退化数据,因此,有必要合理利用这2 种数据来计算模型中的未知参数。目前,已有学者采用融合多源信息的方法进行剩余寿命预测[30-32]。例如,由于加速退化测试数据与现场退化数据存在不同应力,Wang 等[30]提出了一种基于联合似然函数的贝叶斯评估方法,将加速退化测试数据与失效寿命数据相结合。Pang 等[31]进一步研究了基于非线性维纳退化过程的融合加速退化测试数据与失效寿命数据的方法。Zhang 等[32]提出了一种新的贝叶斯框架,用于融合二元退化数据和失效寿命数据进行可靠性分析。然而,这些文献都没有考虑随机效应的影响。最近,Tang 等[33]证明,考虑随机效应的剩余寿命预测在理论上会得到更好的剩余寿命预测结果,但文献[33]在估计未知参数时只利用同类设备的历史退化数据,没有融合失效寿命数据。Tang 等[29]针对基本线性维纳过程和非线性维纳过程提出了一种融合失效寿命数据并考虑随机效应的剩余寿命预测方法。之后,王凤飞等[34]进一步提出了一种融合多源信息并考虑随机效应的剩余寿命预测方法,并通过与仅使用退化数据或失效寿命数据的预测方法进行对比分析,验证了其方法的优越性。然而,由于测量仪器和环境等因素的影响,测量的退化数据可能存在测量误差,不能直接反映真实的退化状态[35]。Si 等[36]考虑了随机效应、退化过程不确定性和测量误差3 层不确定性对剩余寿命预测的影响,提出了基于Kalman 滤波算法的随机参数在线更新方法,并得到了剩余寿命分布的解析表达式。对于存在测量误差的退化设备,Tang 等[37]证明了如果不考虑测量误差的影响可能会导致过早维护,从而增加维护成本。因此,在剩余寿命预测过程中需要考虑测量误差的影响。最近,Yang等[38]基于隐含线性维纳过程提出了一种考虑随机效应的融合多源信息剩余寿命预测方法,并通过实验验证了其方法的有效性。然而,对于隐含非线性维纳退化过程,文献中尚未查阅有学者做过相关工作。
综上所述,在先验退化信息不完美和缺失情况下的剩余寿命预测方法还没有得到充分研究。因此,本文主要基于隐含非线性维纳退化过程模型进行融合多源信息的剩余寿命预测研究。首先,得出了隐含非线性维纳过程模型参数估计的性质,这个工作在文献中尚未有学者报道过。其次,利用参数估计的性质,基于隐含非线性维纳过程模型,提出了融合多源信息的剩余寿命预测方法。当先验退化信息不完美时,该方法使用现场退化数据估计模型固定参数,然后使用失效寿命数据估计漂移参数先验信息。当先验退化信息缺失时,该方法通过融合失效寿命数据和历史退化数据估计模型先验参数。然后,在上述2 种情况下,基于现场退化数据在线更新漂移参数和实际退化状态。最后,通过仿真数据和2 个实例验证了该方法的有效性。
1 隐含非线性维纳退化过程模型参数估计的性质
先验参数描述设备的共同退化特征。准确估计模型先验参数,有助于提高剩余寿命预测的精度。在工程应用中,经常会遇到带有测量误差的非线性退化系统,线性退化模型可能会导致参数估计结果偏离真实值,进一步导致剩余寿命预测精度降低[19]。因此,本节基于隐含非线性维纳退化过程模型分析参数估计的性质。
令Y(t)表示设备在t 时刻测量的退化状态,则退化过程可表示为
式中:x0为设备初始退化状态;λ 为漂移参数表征设备退化速率;b 为非线性系数;σB为扩散系数;B(t)为标准布朗运动,表示退化过程的不确定性;ε 为测量误差。不失一般性,令x0=0。
假设有n 个同类设备,每个设备在相同时刻t1,t2,…,tm检测退化状态,则第i 个设备在ti时刻的监测值可表示为
令Δyi,j=yi(tj)-yi(tj-1),其 中1 ≤i ≤n,1 ≤j ≤m,λi表示第i 个设备的退化速率,εi,j表示第i 个设备 在ti时 刻的测 量误差。则Δyi,j可 表示为
通过MATLAB 函数“FMINSEARCH”最大化式(8)所示的未知参数的对数似然函数ln L,可以得出参数ϕ 的估计值,接着将其代入式(5)~式(7),可 得和的 值,进 一 步 可 得 到参数σ2
ε。
目前已有学者给出了基本线性维纳退化过程模型[29]和隐含线性维纳退化过程模型[38]的无偏参数估计性质。文献[40]给出了隐含非线性维纳退化过程模型无偏估计参数的期望,如引理1所示。引理1[33]隐含非线性维纳过程无偏估计参数和的期望为
更多的证明细节参见文献[40]。然而,从引理1 并不能得知参数估计的精度与哪种因素有关,因此,本节进一步推导无偏估计参数的方差表达式,以获取更多信息。具体结果在定理1 中给出。
定理1 隐含非线性维纳退化过程模型无偏参数估计参数μ̂λ、σ2B和σ2λ的方差为
上述已经获得了隐含非线性维纳退化过程模 型 的 未 知 参 数和的 方 差。同 样 地,也需要进行分析。令P=φΩ+F,其中φ=,那 么,则的表达式可表示为
具体推导过程不再重复。
基于定理1 和定理2,可以得出以下结论:
1) 根据式(10)、式(12)和式(13)可以得知,隐含非线性维纳退化过程模型的参数μλ和σ2λ的估计精度主要受到单元数量和检测时间长度影响。单元数量n 越多,检测时间tm越长,得到的参数估计结果越接近真实值。因此,当历史退化数据缺失甚至没有时,将失效寿命数据融合到退化模型中能够在一定程度上提高μλ和σ2λ的估计精度。
2) 根据式(11)和式(16)可以得知,表示模型退化不确定性的和估计精度与单元数量n和检测次数(m-1)成正比。换句话说,在估计模型未知参数时,使用的数据量越多,估计的和σ2ε越接近真实值。
值得注意的是,上述2 点结论都是假设非线性系数b 为真实值。然而,非线性系数b 的估计是否影响上述结论以及非线性系数b 的估计精度与哪种因素有关,这里很难从理论上进行分析。本文在第4 节通过仿真实验说明非线性系数b 的参数估计性质,从仿真结果可以看出,对于隐含非线性维纳退化过程,其参数估计与σ2B和σ2ε的参数估计具有相似的性质。
2 隐含非线性维纳退化过程模型剩余寿命预测
2. 1 基于Kalman 滤波算法参数在线更新
在维纳退化过程模型参数中,漂移参数的随机性描述同类设备之间的个体差异[41]。为了适应被评估设备的个体退化特征,需要使用现场退化数据对漂移参数在线更新。由于检测的退化数据存在测量误差,不能直接反映真实的退化状态。因此,可以使用Kalman 滤波算法对漂移参数在线更新,并实时估计设备当前退化状态[20]。
对于式(1)所示的隐含非线性维纳退化过程,当检测到被评估设备在tk时刻的退化状态Y1:k时,tk时刻的状态空间方程可表示为[20]
式 中:ψk=σBB(tk)-σBB(tk-1) 表 示tk时 刻 的σBB(tk)与σBB(tk-1)的差值;λk为漂移参数;xk表示tk时刻的真实退化状态;yk表示tk时刻测量的退 化状态;εk表示tk时刻的测量误差;{ψk}k≥1和{εk}k≥1独立同分布。
由于测量误差的影响,真实退化状态xk和漂移参数λk都是隐含状态,为便于公式推导,进一步将式(17)状态空间方程转化为
式中:zk表示tk时刻的状态最优的估计值;Ak表示tk时刻的状态转移矩阵;ηk表示tk时刻状态方程中噪声矩阵;C 表示测量方程的观测矩阵。
根据文献[20],可以通过Kalman 滤波算法更新上述状态方程。令表示在k个退化数据条件下tk时刻的真实退化状态估计值,表示在k 个退化数据条件下tk时刻设备的漂移系数,表示tk时刻真实退化状态的方差,表示tk时 刻 漂 移 系 数 的 方 差,表示tk时刻真实退化值与漂移系数的协方差,则隐含非线性维纳过程模型的漂移参数在线更新结果和估计的当前退化状态可表示为
2. 2 剩余寿命预测
剩余寿命是指设备在当前时刻距离失效时刻的时间长度[2]。定义设备失效阈值为w,在tk时刻被评估设备的观测数据为Y0:k={ y0,y1,…,yk},真实退化状态为X0:k={ x0,x1,…,xk}。根据首达时间的概念[29,42],一旦获得设备在tk时刻的真实退化量X0:k,则剩余寿命可以表示为
由于测量误差的影响,真实退化量xk为隐含状态,不能直接用于剩余寿命预测。针对该问题,基于Kalman 滤波算法参数更新结果,可以得出考虑状态估计的剩余寿命PDF 表达式,具体推导过程参见文献[20]。
3 隐含非线性维纳过程先验参数估计
3. 1 融合失效寿命数据的先验参数估计
在实际剩余寿命预测中,经常会遇到先验退化信息不完美的情况,传统的MLE 方法可能无法估计模型先验参数或错误地估计模型先验参数。为解决这个问题,Tang 等[29]提出了一种合理融合失效寿命数据和现场退化信息的剩余寿命预测方法。然而,Tang 等[29]没有考虑测量误差的影响,这可能会增大剩余寿命预测的不确定性,因此本节在文献[29]的基础上,进一步提出针对隐含非线性维纳过程模型的融合失效寿命数据方法,其流程如图1 所示。

图1 融合失效寿命数据剩余寿命预测流程Fig.1 Flow of remaining useful life prediction based on failure time data fusion
根据第2 节得出的参数性质可知,σ2B、b 和σ2ε的估计精度与现场退化数据的使用量成正比,因此,在该预测方法实施过程中,每当检测到1 个新的现场退化数据就需要将图1 的流程重新执行1 次。
定义y0:m={ y0,y1,…,ym}为现场退化数据,T1:n′={T1,T2,…,Tn′}为n′个 设 备 的 失 效 寿 命 数据或是首次达到失效阈值w 的失效时间数据,则融合失效寿命数据剩余寿命预测方法的先验参数估计分为2 个步骤。
第1 步 基于现场退化数据,使用MLE 获取先验固定参数、b 和σ2ε。
对于单个设备的退化过程建模,由于不存在个体之间的差异,因此在建立隐含非线性维纳退化过程模型时,不考虑随机效应的影响,视λ 为 固定系数。基 于式(1),令Δyj=yj-yj-1,,Δtj=tj-tj-1,1 ≤j ≤m,Δy=[Δy1,Δy2,…,Δym]T,Δv=[ Δv1,Δv2,…,Δvm]T,Δt=[ Δt1,Δt2,…,Δtm]T。则 有σε2F),其中Ω=diag{ Δt1,Δt2,…,Δtm},F 的元素见式(4),f1,1=1。令D=Ω+ϕF,其中,则单个设备的对数似然函数可表示为
将式(26)代入式(24),则可以得到b 和ϕ 的剖面似然函数表达式为
通过MATLAB 的“FMINSEARCH”函 数最大化式(27)可以获得b 和ϕ 的估计值。将其代入式(25)和式(26)可以得到λ 和,进一步得到估计值。
第2 步 使 用 失 效 寿 命 数 据 求 取μλ和σ2λ的先验分布。
根据Peng 和Tseng[42]的结论,隐含维纳退化过程寿命分布不受测量误差影响。则在给定和 失 效 寿 命 数 据T1:n′={T1,T2,…,Tn′}时,根 据非线性维纳过程的性质,第v 设备的故障时间Tv服 从 逆 高 斯 分 布[29],其中1 ≤v ≤n′。Tv的 似 然函数L 为
根据式(28),失效寿命时间关于λv的对数似然函数可以表示为
给定非线性模型的失效寿命数据T1:n′={T1,T2,…,Tn′},则 可以通 过最大化 式(29)得 到λ={ λ1,λ2,…,λn′}。接 下 来,先 验 漂 移 参 数可 以通过式(30)计算。
3. 2 融合多源信息的隐含非线性维纳过程先验参数估计
当先验退化信息缺失且同时存在先验退化信息和失效寿命数据时,根据第2 节获取的参数估计性质可知,通过融合尽可能多的先验退化数据可以提高模型未知参数估计的精度。最近,王凤飞等[34]针对该问题提出了融合多源信息并考虑随机效应的剩余寿命预测方法。然而,文献[34]并没有考虑测量误差的影响,本节将该方法进一步推广到隐含非线性维纳退化过程,具体流程如图2所示。

图2 融合多源信息剩余寿命预测流程Fig.2 Flow of remaining useful life prediction based on multi-source information fusion
第2 步 基于历史退化数据和失效寿命数据计算先验漂移参数μλ和σ2λ。
假设有n 个同类设备,每个设备在相同时刻t1,t2,…,tm检测退化状态,基于式(1),令yi,j表示第i 个 设 备 在tj时 刻 测 量 的 退 化 状 态,Δyi,j=yi(tj)-yi(tj-1),,Δtj=tj-tj-1,Δyi=[Δyi,1,Δyi,2,…,Δyi,m]T,Δv=[ Δv1,Δv2,…,Δvm]T,Δt=[ Δt1,Δt2,…,Δtm]T和,其中,1 ≤i ≤n,1 ≤j ≤m,λi表示第i 个设备的退化 速 率。 则Δyi服 从 均 值 为μλΔv,方 差 为的多元正态分布。此外,假设存在n′组失效寿命数据T1:n′={T1,T2,…,Tn′},Tv为第v 个单元的失效寿命数据,其中1 ≤v ≤n′。令D=Ω+ϕF,其中。受文献[34]启发,的剖面对数似然函数可以表示为
通过MATLAB 函数“FMINSEARCH”最大化式(31),可以得到μλ和的估计值。
融合多源信息是指融合历史退化数据信息、失效寿命数据信息和被评估设备现场退化数据信息。然而,当先验退化信息不完美时,如果基于传统的极大似然方法直接使用该数据估计模型的未知参数,可能会导致参数的估计结果偏离真实值较远,从而导致剩余寿命预测结果精度偏低。对于这一特殊情况,在使用融合多源信息剩余寿命预测方法时,可以将历史退化数据转换成失效寿命数据,仅融合失效寿命数据信息和被评估单元现场退化数据信息进行剩余寿命预测。
4 实 验
本节通过仿真实验和2 个实例来验证文章提出方法的有效性和优越性。首先,使用蒙特卡罗算法生成隐含非线性维纳退化过程的仿真数据以验证第2 节获取的参数估计性质。然后,使用锂电池退化数据验证在先验退化信息不完美情况下的优越性,使用疲劳裂纹数据验证在先验退化信息缺失情况下的优越性。
4. 1 仿真实验
Yang 等[38]分析了隐含线性维纳退化过程模型的参数性质,得到了参数估计精度与单元数量和检测次数以及检测时间成正比的结论。然而,对于隐含非线性维纳退化过程模型,非线性系数b 的参数估计性质难以通过理论推导得出,且当非线性系数b 为估计值时,第2 节获取的性质是否会受到影响有待验证。本节试图使用仿真实验获取影响非线性系数b 估计精度的因素,以及进一步验证第2 节的参数估计性质。
假 设 模 型 参 数 为μλ=1,=0.04,=0.25,b=1.5,=4,令单元数量N=80,每个单元在相同的时刻检测退化数据,检测次数m=40,检测时间间隔Δt=1 h。仿真数据的部分单元退化路径如图3 所示。为了研究退化数据特征与参数估计精度之间的关系,分别使用5、20 和80组单元退化数据估计模型参数,来验证单元数量对参数估计精度的影响。此外,每当生成1 个新的退化数据就将参数再估计1 次,以验证检测时间长度和检测次数对参数估计精度的影响。由于仿真数据随机生成,如果仅用1 次生成数据估计参数,其估计结果有可能难以完全体现退化数据与参数估计精度之间的关系。因此使用相同的方法生成20 次退化数据,每一次的参数估计方式相同。估计的参数变化曲线结果如图4~图8 所示。
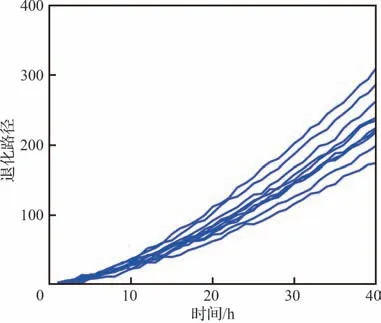
图3 部分仿真退化路径Fig.3 Some degradation paths
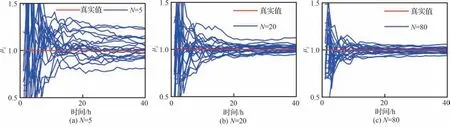
图4 μλ 随单元数量N 变化的参数估计结果Fig.4 Estimation of μλ with change of number N of units
从图4 和图5 可以看出,参数估计变化曲线在使用单元数量N 相同时,退化数据检测时间tm越长,得到的参数估计结果越接近真实值。这是因为检测时间tm越长,式(10)、式(12)和式(13)中Δv′D-1Δv 数值越大,所以估计得到的μλ和不确定性越小,估计结果越准确。此外,当检测时间达到一定数值时,参数估计结果随着检测时间长度的增加发生的变化不明显,而通过增加单元数量N,参数的估计精度可以得到进一步提升,这是因为此时式(10)和式(12)中的和式(13)已经很小,μλ和σ2λ的估计精度主要受到n的影响。因此,当先验退化信息不完美时,仅使用失效寿命数据用来估计退化模型的先验漂移参数可以确保其估计精度,其中失效寿命数据反映单元数量N。当同时存在失效寿命数据和退化数据时,合理地将2 种退化数据融合能够进一步提高模型先验漂移参数估计的精度。

图5 σ2λ 随单元数量N 变化的参数估计结果Fig.5 Estimation of σ2λ with change of number N of units
从图6 和图7 可以看出,在整个仿真周期内,当使用单元数量N 相同时,随着检测次数的增加,参数估计变化曲线逐渐向真实值收敛,当检测次数m 相同时,使用的单元数量N 越多,参数估计结果越准确,这是因为式(11)和式(16)的数值与n(m-1)成反比,即和σ2ε估计精度与检测次数和单元数量成正比。值得注意的是,从图8 可以看出,非线性系数b 的参数估计变化曲线与图6和图7 具有相同特征,即b 的估计精度同样与单元数量和检测次数成正比。因此,在剩余寿命预测过程中,如果能够获取的现场退化数据很多,如4.2 节的锂电池退化数据,则在先验退化信息不完美的情况下,当现场退化数据检测次数m很大时,可以不使用历史退化数据估计模型固定参数。
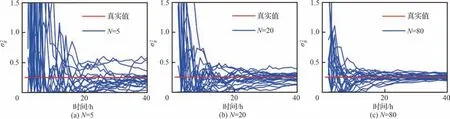
图6 σ2B 随单元数量N 变化的参数估计结果Fig.6 Estimation of σ2B with change of number N of units

图7 σ2 ε 随单元数量N 变化的参数估计结果Fig.7 Estimation of σ2 ε with change of number N of units

图8 b 随单元数量N 变化的参数估计结果Fig.8 Estimation of b with change of number N of units
综上分析,仿真实验验证了第2 节的参数估计性质,得出了参数估计性质不受非线性系数b影响的结论,并获取了影响非线性系数b 估计精度的影响因素,为文章针对隐含非线性维纳过程提出的融合多源信息方法进行剩余寿命预测奠定了理论基础。
由图4~图8 可以看出,隐含非线性维纳退化过程模型各个参数的收敛程度不同。这是因为参数估计的方差数值越大,参数估计结果的不确定性越大,因此收敛程度越差。根据第2 节推导的参数估计方差表达式可知,退化数据特征对不同的参数的影响不同,因此各个参数的收敛程度存在差异。
4. 2 融合失效寿命方法剩余寿命预测
本节使用NASA 发布的锂电池容量退化数据,验证文章提出的考虑测量误差且融合多源信息的剩余寿命预测方法在先验退化信息不完美的情况下剩余寿命预测的有效性。该数据由4 个同类型的锂电池在室温下以充电、放电和阻抗测量3 种工作模式反复循环的容量退化数据组成[43]。锂电池长时间的休息可能会出现容量再生现象,又称弛豫效应[44]。在实际使用过程中,由于不同的锂电池休息时间不固定,可能会导致剩余寿命无法准确预测,因此需要将原始数据中的弛豫效应消除,消除弛豫效应后的锂电池容量退化路径如图9 所示。如何消除弛豫效应的更多细节参见文献[27,44]。通常,当电池容量退化到额定容量的70%~80% 时,电池被认为失效[27]。本节实验中假设锂电池失效阈值为额定容量的70%(1.4 A·h),并选择B0007 电池为被评估单元,其他电池用于模型先验参数估计。

图9 锂电池容量退化路径Fig.9 Degradation paths of lithium battery capacity
从 图9 可 以 看 出,B0005 和B0007 电 池 的 容量退化曲线具有非线性特征,而B0006 和B0018电池的容量退化曲线具有线性特征,如果直接使用历史退化数据估计模型参数,会弱化非线性特征,从而降低剩余寿命预测精度[29],这种情况被视为先验退化信息不完美。实际上,这4 组退化数据不仅包含了退化数据信息,同时也包含了寿命数据信息,可以利用其寿命数据信息预测剩余寿命[29],此时使用B0005、B0006、B0018 电池的寿命数据预测B0007 电池的剩余寿命就是特殊情况下的融合多源信息方法的剩余寿命预测问题。为简单起见,将文章提出的考虑测量误差且融合失效寿命数据的剩余寿命预测方法称为M0,文献[29]中提出的非线性融合失效寿命数据方法称为M1,文献[20]中基于隐含非线性维纳退化过程模型,仅使用历史退化数据估计模型未知参数的常用剩余寿命预测方法称为M2。根据消除弛豫效应的数据,可以计算出B0005、B0006 和B00018 的失效时间分别为85.55、69.35 和51.02 次循环,这些时间被用来计算M0和M1的先验漂移参数。
图10为被评估单元部分时刻的剩余寿命分布,图11 为被评估单元在第100 次循环的剩余寿命分 布。从 图10 和 图11 可以看出,M0、M1和M2的剩余寿命分布都能够覆盖真实的剩余寿命值,且M0的图形比M1和M2的图形更集中于真实的剩余寿命值,这说明M0具有更高的预测精度。M0和M1的图形对比说明,考虑测量误差能够提高剩余寿命预测精度。此外,通过对比M1和M2可知,虽然M2考虑了测量误差的影响,但其剩余寿命的预测精度仍然比M1差,说明先验退化信息不完美可能会导致剩余寿命预测结果出现更大的偏差。

图10 基于锂电池数据不同循环次数估计的剩余寿命分布Fig.10 Estimated remaining useful life at different cycle times based on lithium battery data
接下来从参数实时变化曲线来分析3 种预测方法的剩余寿命预测效果,如图12 所示。图12中,M2估计的始终比M0大,这是因为B0006和B0018 电池退化过程具有线性退化特征,导致M2估计的非线性系数b 偏小如图12(c)所示,这进一步导致M2无法有效地跟踪被评估电池的退化特征,于是被评估电池的部分非线性退化特征体现到了上。除此之外,M1估计的始终大于M0,这是因为M1没有考虑测量误差的影响,B0007 电池退化的不确定性都由体现。不同的是,对于M0,B0007 电池退化的不确定性由和σε2分担。通常,越小,得到的分布图形越尖锐,剩余寿命预测结果的不确定性越小。因此,这进一步体现了M0方法的优越性。

图12 M0、M1 和M2 在不同时刻的后验参数Fig.12 Posterior parameters of M0, M1 and M2 at different cycle times
为了能够更直观地区分3 种预测方法的预测效果,计算各模型剩余寿命的均方误差(Mean Squared Errors,MSEs)。第k 次循环的MSEs 计算表达式为
图13 展示了3 种预测方法剩余寿命的MSEs,图中M0的MSEs 始终小于M1和M2,这说明M0的预测精度高于M1和M2。总的来说,在先验退化信息不完美的情况下,融合失效寿命数据方法能够提高模型的参数估计精度,进一步提高剩余寿命预测的精度。此外,对于带测量误差的退化设备,预测剩余寿命时考虑测量误差影响是必要的。
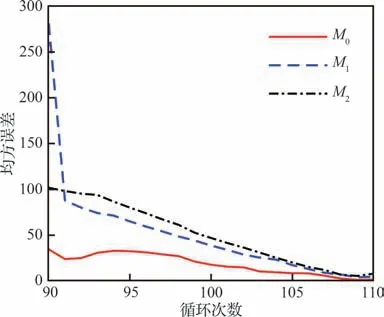
图13 M0、M1 和M2 方法估计的剩余寿命均方误差Fig.13 MSEs of remaining useful life of M0, M1 and M2
4. 3 融合多源信息方法剩余寿命预测
本节使用铝合金疲劳裂纹退化数据验证本文提出的考虑测量误差且融合多源信息的剩余寿命预测方法在先验退化信息缺失的情况下的有效 性。原 始 数 据 取 自Lu 和Meeker[45],该 实 验测试了21 个产品的裂纹长度,测试频率为1 万次循环。如果产品的裂纹长度超过40.64 mm,则被视为失效。在实验验证中使用终止时间为9 万次循环的21 组退化数据,退化路径如图14 所示,详细的数据介绍及使用方法参见Wang 等[46]。为了便于验证融合多源信息方法的有效性,假设21 组退化数据中1 组退化数据为被评估单元的现场退化数据,6 组退化数据为历史监测数据,14 组退化数据仅能获取其失效寿命[34]。为简单起见,定义本文提出的考虑测量误差的融合多源信息剩余寿命预测方法为M3。

图14 疲劳裂纹退化路径Fig.14 Degradation paths of fatigue crack
本节实验以图14 中的红色实线为被评估单元退化数据,蓝色虚线为历史退化数据,用于估计M2的模型未知参数,黑色点划线为失效寿命数据,根据失效阈值w=17.78 mm[34]计算其失效时间,用作M0和M3的失效寿命数据。M0估计的先验参数如表1 所示。M2估计的先验参数为,。M3估计的先验参数为μλ=9.503,,,b=1.295,。

表1 M0在不同时刻的先验参数Table 1 Prior parameters of M0 at different times
图15 展示了被评估单元在部分时刻的剩余寿命分布,图16 为被评估单元在9 万次循环的剩余寿命分布。从图15 和16 可以看出,M0和M2的剩余寿命分布都偏离真实剩余寿命值较远,仅M3能够较好地覆盖真实剩余寿命值,这说明M3的预测效果优于M0和M2。

图15 基于疲劳裂纹数据不同循环次数估计的剩余寿命分布Fig.15 Estimated remaining useful life at different cycle times based on fatigue crack data
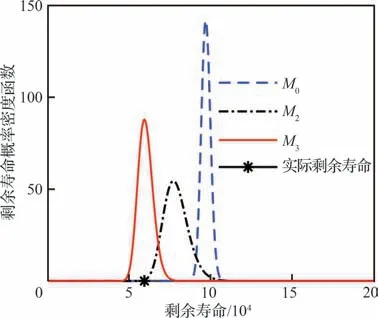
图16 在9 万次循环M0、M2和M3估计的剩余寿命分布Fig.16 Estimated remaining useful life of M0,M2 and M3 at 0.09 million cycles
图17为3 种预测方法的后验漂移参数实时变化曲线。从3 种方法的模型先验参数和后验漂移参数的估计结果可知,M2估计的模型固定参数与M3相同。然而,M0估计的b 和均小于M2和M3的估计值。根据第2 节参数估计性质和4.1 节仿真实验可以得知,和b 的估计精度与单元的数量和检测次数成正比。出现和b 偏小的原因是被评估设备现场退化数据的不确定性小,且检测次数m 较少(即式(11)中的m 较小),从而导致和b 的估计结果出现较大偏差。值得注意的是,由于M0估计的b 和偏小,在融合失效寿命数据时,导致了M0的漂移参数在贝叶斯框架下受到影响,进一步导致剩余寿命预测出现失败。这说明对于现场退化数据较少的设备,融合失效寿命数据剩余寿命预测方法可能无法准确预测剩余寿命。图18 展示了3 种预测方法在不同时刻的剩余寿命的MSE。图中,M3的MSE 整体上小于M0和M2,这说明M3具有更好的预测效果。总的来说,将尽可能多的先验退化信息合理融合能够提高模型参数估计精度,进而提高剩余寿命预测的精度。

图17 μλ 和在不同循环次数的后验参数Fig.17 Posterior parameters of μλ and at different cycle times
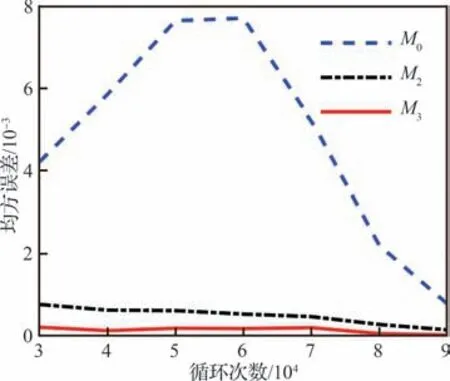
图18 M0、M2 和M3 方法估计的剩余寿命均方误差Fig.18 MSE of remaining useful life of M0, M2 and M3
为了验证文章提出的考虑测量误差且融合多源信息剩余寿命预测方法对带有测量误差的退化系统能够提高剩余寿命预测的精度,定义文献[34]提出的非线性融合多源信息的剩余寿命预测方法为M4。图19 为被评估单元在部分时刻的剩余寿命分布,图20 为被评估单元在9 万次循环的剩余寿命分布。从图19 和图20 可以看出,M3和M4的剩余寿命分布都能很好地覆盖真实的剩余寿命值,但由于疲劳裂纹退化数据的测量误差较小,M3和M4的分布图形十分接近。

图19 不同循环次数M3和M4估计的剩余寿命分布Fig.19 Estimated remaining useful life of M3 and M4 at different cycle times
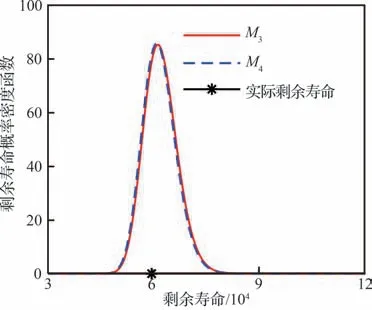
图20 在9 万次循环M3和M4估计的剩余寿命分布Fig.20 Estimated remaining useful life of M3 and M4 at 0.09 million cycles
为了显著比较考虑测量误差的效果,这里在原始疲劳裂纹退化数据的基础上适当增加1 个方差为0.003 的正态分布误差。
与图13 的数据设 定相同,图21 为M3和M4在部分时刻的剩余寿命分布,从图21 可以看出,M3的剩余寿命分布图形比M4更窄,且M3的分布图形更集中于真实剩余寿命值,这一结果表明,在退化数据存在测量误差的情况下,使用M3能够得到比M4更好的预测效果。接下来,计算不同时间点的MSE,如图22 所示。可以看出M3的MSE 始终远小于M4,这进一步体现了文章提出的剩余寿命预测方法的优越性。总的来说,对于带测量误差的退化系统,考虑测量误差影响是必要的。
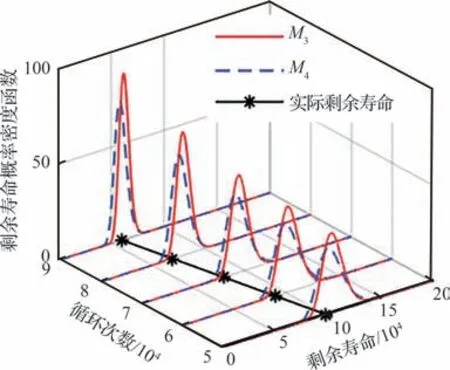
图21 增加测量误差情况下M3 和M4 估计的剩余寿命分布Fig.21 Estimated remaining useful life of M3 and M4 with additional measurement errors

图22 M3 和M4 方法估计的剩余寿命均方误差Fig.22 MSE of remaining useful life of M3 and M4
5 结 论
准确的参数估计是保证剩余寿命预测精度的前提。本文首先分析了隐含非线性维纳退化过程模型参数估计的性质。然后,基于这些性质,针对隐含非线性维纳退化过程,提出了一种融合多源信息的剩余寿命寿命预测方法。最后,通过仿真实验和2 个实例验证了参数估计性质和所提剩余寿命预测方法的有效性。综上所述,本文的主要贡献可以总结如下:
1) 基于隐含非线性维纳退化过程的无偏参数估计结果,推导得到了模型参数的方差,分析得到了隐含非线性维纳退化过程的参数估计精度与单元数量、检测时间长度和检测次数之间的关系,为合理融合多源信息进行剩余寿命预测提供了理论依据。
2) 针对带有测量误差的随机退化系统,为应对先验退化信息不完美或缺失等问题,提出了一种合理融合多源信息的剩余寿命预测方法。

