以能量表征的平面应变及平面应力Ⅰ型裂纹J 积分解
冯子夜,蔡力勋,于思淼
西南交通大学 力学与航空航天学院,成都 610031
J 积分作为一个定义明确、理论严谨的弹塑性断裂力学基础参量,既能表征裂纹尖端应力应变场程度,又能与加载过程中能量相关而可以通过试验进行测定,因此, J 积分理论表征对于含裂纹结构的安全评价有重要意义。
1921 年,Griffith[1]提出 了 能 量平 衡 理 论,奠定了断裂力学基础。1957 年,Irwin[2]提出了应力强度因子概念,并与能量释放率建立联系,使断裂力学进入新阶段。1967 年和1968 年,Cherepanov[3]和Rice[4]独 立 提 出 了J 积 分 概 念,不 久,Rice[5]和Hutchinson[6]等,提 出 了 描 述 平 面 裂 纹的裂尖弹塑性应力应变场理论解,即HRR 场奇异解,为弹塑性断裂力学发展奠定了基础。1972 年,Begley 和Landes[7]提 出 了 以J 积 分 为 控制参量的弹塑性断裂准则,将J 积分作为延性材料裂纹试样断裂判据,在材料与结构弹塑性裂纹问题的安全评价中得到应用。1981 年,Kumar等[8-9]基 于Shih 和Hutchinson[10-11]所 提 出 的 对Ⅰ型裂纹试样J 积分与载荷关系的方程,针对6 种裂纹试样,通过大量有限元计算编制了用于插值求解材料弹塑性J 积分的、含大量离散式有限元分析数据表格的EPRI(Electric Power Research Institute)手册。EPRI 手册数据应用繁琐,并未得到广泛工程应用。20 世纪90 年代,为研究平面约束度对J 积分的影响,O’Dowd、Shih、Chao 和Nikishkov 等 陆 续 提 出 了 的J-Q[12-13]理 论、J-A2理论[14-15]、J-A 理论[16-18],对不同的材料及几何形状进行了一系列详细的有限元分析,计算量很大。
在现有方法中,J 积分的计算可以分为2 大类:一是按照简化模型或者工程估算方法进行计算,如EPRI 法,二是通过有限元分析或试验方法获取J 积分值。Qian 等[19]利用有限元分析对多种试样的J 积分进行了求解,但理论性不足。贺屹等[20]建立了J 积分-载荷半解析公式,仅求解了平面应变条件下的J 积分。在现行的断裂韧度试验方法[21-22]中,主要对裂纹尖端具有符合平面应变条件的高约束度标准紧凑拉伸 (Compact Tension,CT) 试样、单边裂纹弯曲 (Single Edged notched Bending,SEB) 试 样、圆 形 紧 凑 拉 伸(Round Compact Tensile,RCT)试样[23]等进行试验以获得材料断裂韧度。此外,中心穿透裂纹(Center Cracked Tension,CCT)板试样[24]、双边裂纹拉伸(Double Edge-notched Tension,DET)试样以及C 型拉伸(C-shaped Inside Edgenotched Tension,CIET)试样[25]等也被应用于断裂韧性试验。
材料Ⅰ型裂纹试样的J 阻力曲线均受到几何尺寸的约束影响。在线弹性条件下,K 因子有大量数值公式与解析公式, 不同于K 因子,J 积分较缺乏描述公式,并未形成公式手册。1973 年,Rice 等[26]针 对SEB 试 样 首 次提 出J 积 分 塑 性 分量与2 倍纯塑性应变能成正比的解析方程,同期,陈篪等[27]也独立提出了相同方程。1979 年,Hutchinson 和Paris[28]针对Ⅰ型裂纹提出了纯塑性J 积分与塑性因子ηp的关系方程
式中: B 表示试样厚度;W 为试样宽度;a 为试样裂纹长度;Up表示塑性应变能,可由载荷位移曲线获得;无量纲塑性因子ηp多由有限元分析确定,通过有限元模型计算提取J 积分值,减去弹性部分,根据式(1)逆向求解获得。1980 年,Ernst 和Paris[29]进一步证明了J 积分塑性分量与ηpUp呈正比关系。Donato[30]和Huang[31]等分 别在2006 年和2014 年通过有限元分析对SEB 试样的因子进行了综合分析,认为ηp与材料、几何、变形均相关。
目前为止,学者们所提出的获取J 积分的方法公式形式复杂,缺乏更简易的方式获得形式统一的表达式。本文基于能量密度等效[32-34],考虑有效变形体积效应对含裂纹试样J 积分的影响,提出了以能量表征的、适用于平面Ⅰ型裂纹试样J 积分半解析解。
1 Ⅰ型裂纹试样应变能
弹塑性力学中物理关系,即等效应力应变关系可采用Ramberg-Osgood 律(R-O 律)来表征
式中:σeq、εeq、εe-eq和εp-eq分别为等效应力、等效应变、等效弹性应变和等效塑性应变;E、K、N 分别为弹性模量、应变强化系数和应力强化指数。
对于单向受载、各向同性、材料本构关系为幂律或线性的任一构元,根据积分中值定理,在其有效变形域内存在一个能量密度中值点M[35-36],使得构元的总应变能U 与点M 代表性体积单元(Representative Volume Element,RVE)的应变能密度之间有如下关系
式 中:μM为点M 材料RVE 的应变能密度;Veff为构元的有效变形域体积。进一步地,复杂应力状态下点M 材料RVE 的应变能密度可等效转换为单轴应力状态下RVE 的能量密度[37],即
式中:σij和εij分别为复杂应力状态下的应力张量和应变张量;σeq和εeq分别为简单应力状态下的等效应力和等效应变。
由式(3)和式(4),受载试样在有效变形域内的应变能可表示为
在弹塑性条件下,根据文献[8],单向受载的Ⅰ型裂纹构元试样的总应变能U 可以表为纯弹性应变能Ue与纯塑性应变能Up的工程叠加,即
式中:h、he和hp分别为载荷P 作用下加载线总位移、弹性位移和塑性位移。
结合式(4)、式(5)和式(6),Ⅰ型裂纹试样的无量纲应变能可表示为
式中:m 为有效体积折减指数。在纯塑性条件下,假设
式中:k1和k2分别为塑性位移系数和塑性位移指数。考虑试样点MRVE 的等效应变与等效应力与加载线位移有关,即
式中:k3和k4分别为应变系数和应变指数。则由式(7),塑性应变能Up可表为
式中:mp为纯塑性变形指数;ξp为纯塑性能量-位移曲线的曲度。
在纯线弹性条件下,N=1,由式(7),应变能Ue关于位移的表达式可设为
式中:k0为弹性体积系数。
在弹塑性条件下
2 Ⅰ型裂纹试样J 积分解
在弹塑性条件下,单向受载试样的Ⅰ型裂纹试样在变形过程中,总位移可由按工程叠加得到[9]
由功能原理即
考虑式(11)、(12),以he和hp分别对式(15)分别求导,并结合式(14)可得到表述Ⅰ型裂纹试样弹塑性载荷-位移关系的半解析解
由J 积分的Rice 能量定义
式(11)对裂纹长度a 求导后,结合式(16)和式(17)得到载荷-J 积分方程,无量纲化后可得Ⅰ型裂纹试样的纯塑性J 积分
式中:J*为特征J 积分。结合式(11)、式(16)和式(18)可得Ⅰ型裂纹试样纯塑性能量-J 积分解
同理,可得到I型裂纹试样纯弹性能量-J积分解结合式(19)和式(20)可得到Ⅰ型裂纹试样能量-J 积分解
无量纲简化后可表示为
式中:U*为特征能量,式(22)或式(21)称为基于能量的平面Ⅰ型裂纹J 积分半解析解。
3 模型参数的确定方法
本文模型参数均可由有限元计算确定,标定方法由图1 框图流程所示,固定材料参数E、N 和K,计算不同a/W 的载荷-位移曲线获得参数m;计算不同弹性模量E 确定参数k0;计算不同N 的载荷-位移曲线确定参数k1~k4,文中有限元模型均采用PLANE182 单元,弹性模量E=210 GPa,泊松比v=0.3。表1 给出了不同试样的有限元(FEA)模型及模型适用尺寸。
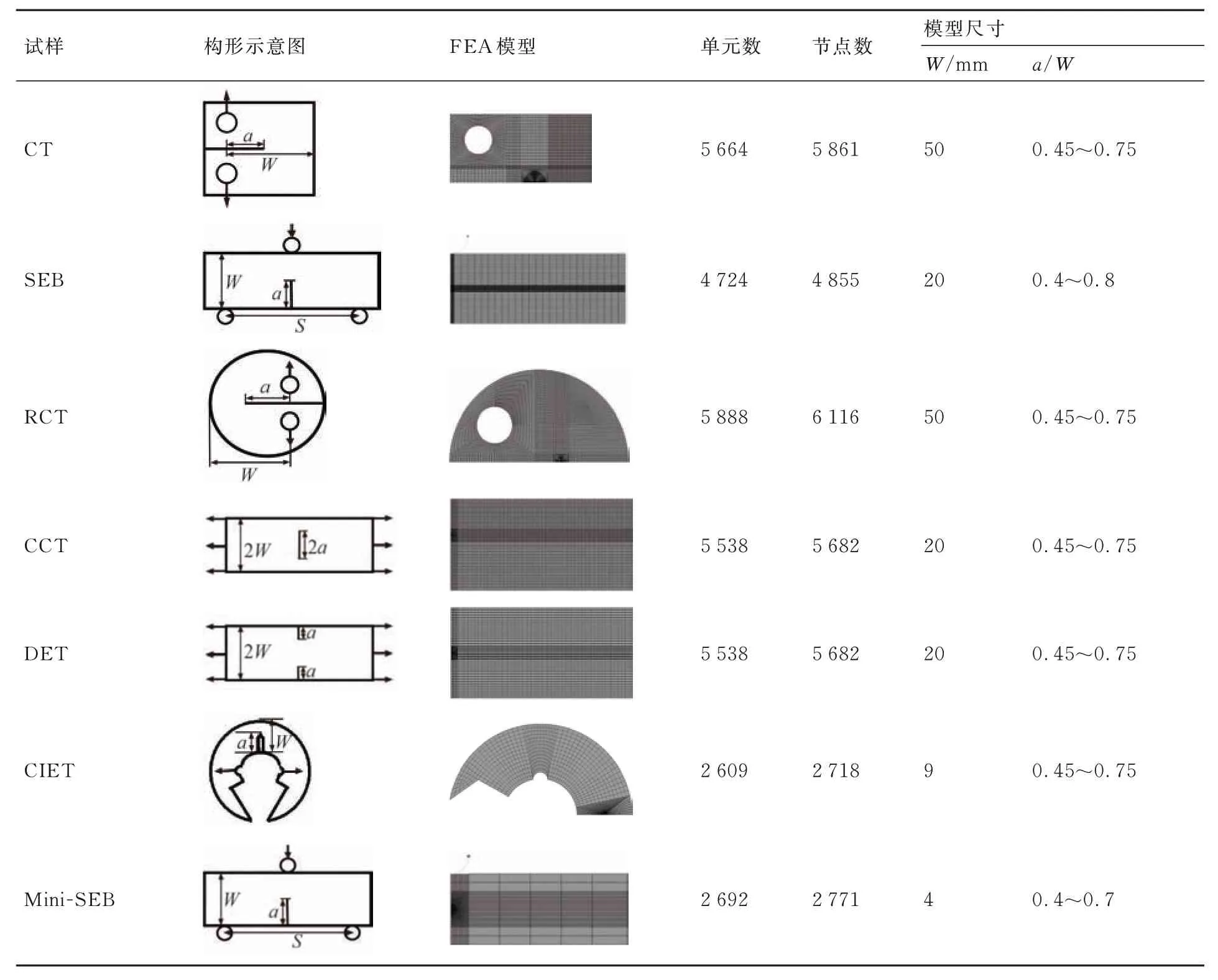
表1 试样FEA 模型及尺寸Table 1 FEA model and dimension of specimens
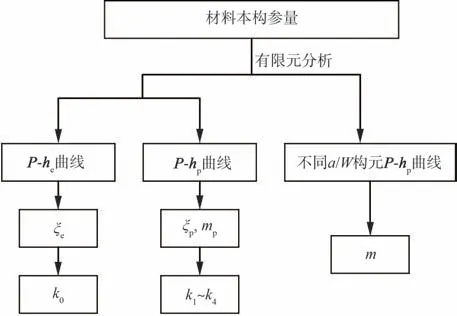
图1 参数标定Fig. 1 Parameter calibration
考虑到有限元模型关键部位网格密度会对计算精度产生较大影响,为提高计算精度,通过网格加密法选取合理的网格密度。定义裂纹尖端0.02 mm 半径内,单元数量为8 时为一倍网格密度,图2 给出了CT 试样裂尖网格划分方式,图3 给出了不同网格密度下计算得到的载荷-位移曲线对比。在保证计算精度的前提下,为提高计算效率,本文选取较疏网格密度模型进行计算。表2 和表3 分别给出了不同试样在平面应变及平面应力条件下的参数标定结果。
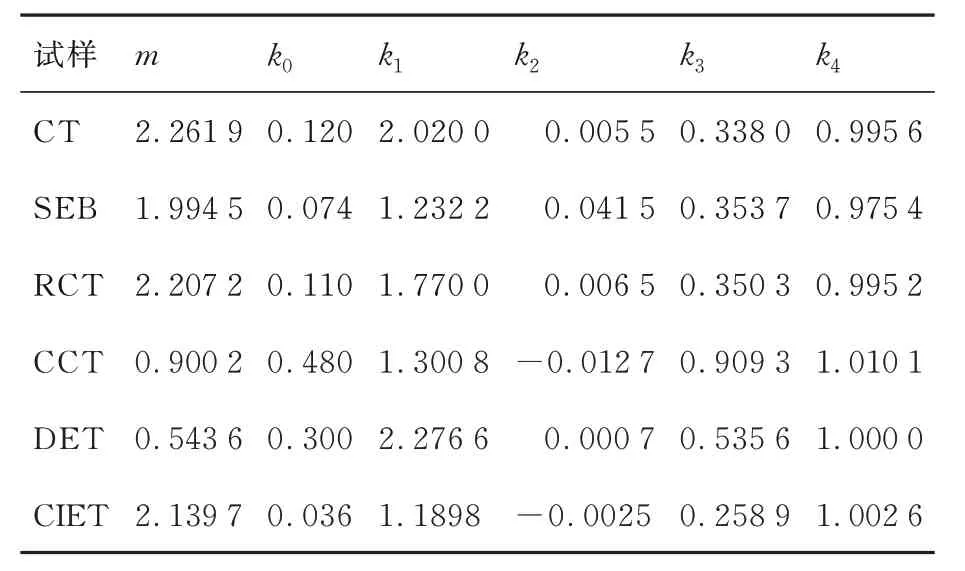
表2 平面应变模型参数标定结果Table 2 Calibration results of plane strain model parameters
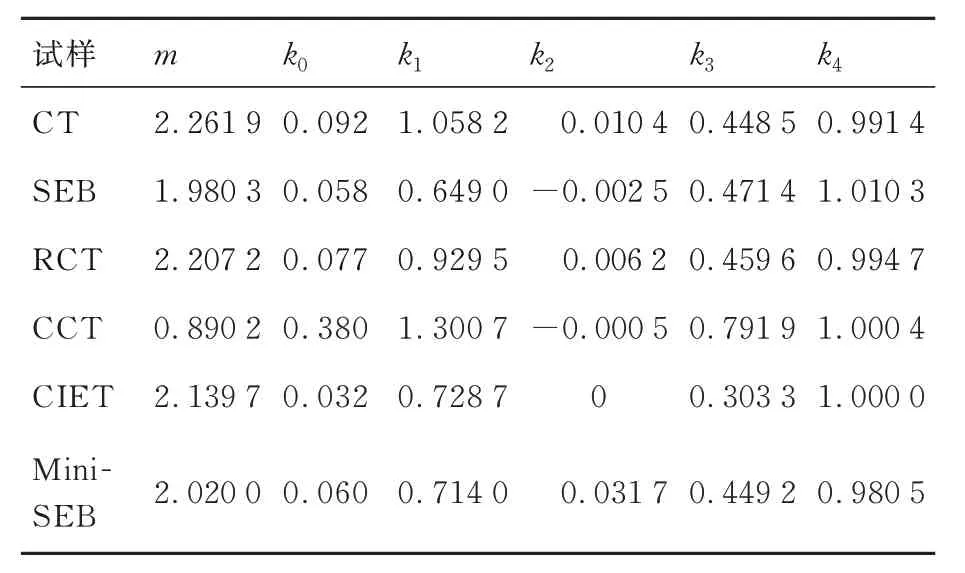
表3 平面应力模型参数标定结果Table 3 Calibration results of plane stress model parameters

图2 裂尖网格划分Fig. 2 Meshing of crack tip
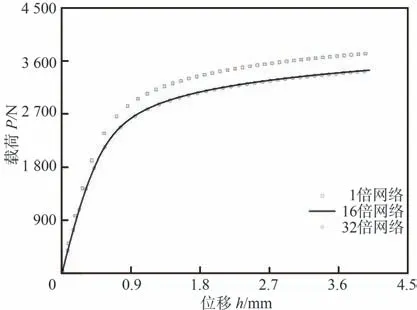
图3 CT 试样有限元网格验证Fig. 3 Finite element mesh verification of CT
4 模型正确性验证
图4 给出了SEB 试样在平面应变条件下不同的a/W、不同K 和N 下Jp/J*-Up/U*的几何无关纯塑性验证曲线。由图可见,模型预测的Jp/J*-Up/U*曲线与有限元分析获得的曲线吻合良好。
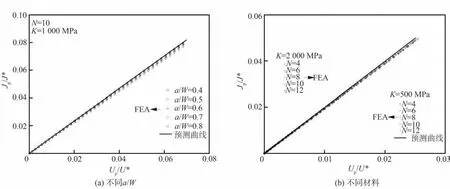
图4 SEB 试样纯塑性Jp/J*-Up/U*曲线Fig. 4 Jp/J*-Up/U* curves for pure plastic SEB specimens under plane strain condition
图5 和图6 给出了不同试样在平面应变及平面应力条件下不同应变强化系数K、不同应力强化指数N 下的J/J*-U/U*曲线。
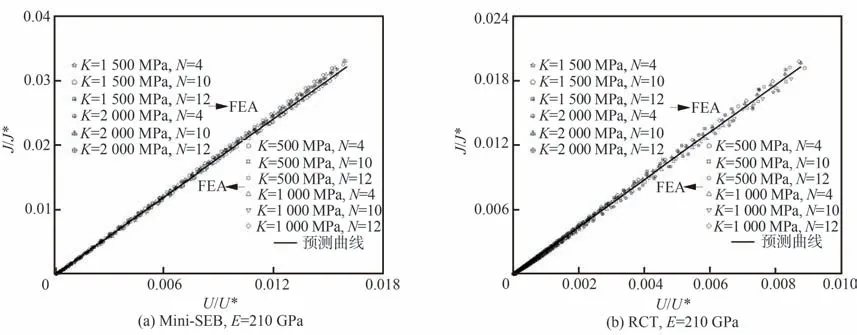
图6 平面应力下弹塑性试样J/J*-U/U*曲线Fig. 6 J/J*-U/U*curves for elastoplasticity specimens under plane stress condition
图7给出了材料参数E=210 GPa,K=1 000 MPa,N=10 下6 种试样不同裂纹长度a/W 与J 积分的预测结果与计算结果的比较。
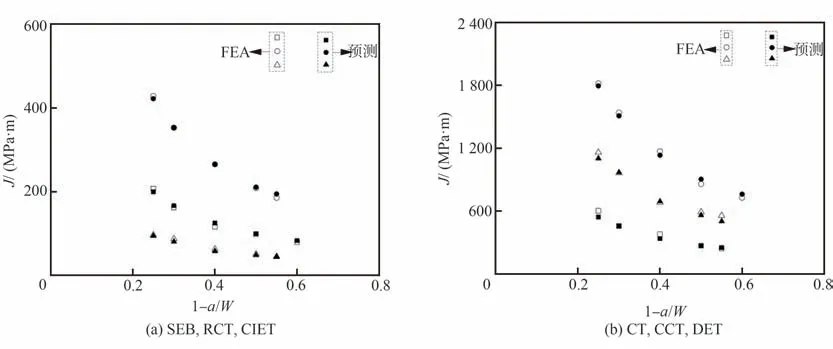
图7 平面应变下弹塑性试样J -(1-a/W)曲线Fig. 7 J -(1-a/W) curves for elastoplasticity specimens under plane strain condition
结果表明,本文所提出的Ⅰ型裂纹全约束J积分关于能量的模型与有限元结果具有良好的一致性,在不同裂纹长度、材料参数下,模型预测曲线与计算结果误差不超过3%,能够很好地预测不同几何尺寸,不同材料试样的能量-J积分关系。
对于材料参数(E、K 和N)未知的试样,可通过相同尺寸的Ⅰ型钝裂纹试样进行加载,得到弹塑性载荷-位移曲线确定材料参数。以SEB 试样为例,在平面应变条件下,假设材料参数未知,对相同尺寸的SEB 钝裂纹试样加载得到弹塑性载荷-位移曲线,取线弹性段载荷-位移曲线,由式(16)可得到E 为
式中:S1为线弹性段刚度。弹塑性位移减去纯弹性位移可得到纯塑性载荷-位移曲线,由式(16),K和N为
式中:S2和mp′分别为纯塑性载荷-位移曲线幂律拟合之后的系数与指数。图8 给出了不同材料有限元输入应力-应变曲线与预测材料参数所得应力-应变曲线,通过式(23)与式(24)所得材料参数E、K 和N 与输入值误差不超过2%。
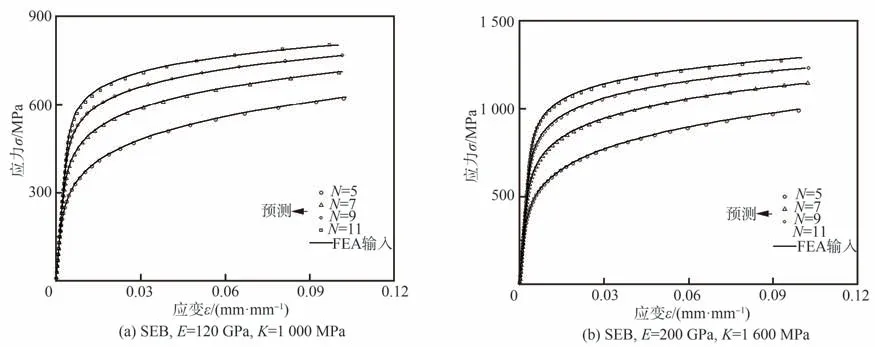
图8 弹塑性应力-应变关系验证Fig. 8 Validation of elastoplasticity stress-strain relationship
5 结 论
1)基于能量密度等效,提出了基于能量的平面应变和平面应力Ⅰ型裂纹弹塑性J 积分的半解析解。
2)针对不同a/W、不同材料的6 类Ⅰ型裂纹试样,基于能量的平面Ⅰ型裂纹J 积分半解析解预测的J 积分-能量关系与有限元分析结果密切吻合。

