鱼雷垂直入水瞬间结构响应的数值模拟*

贺 征，高紫晴，顾 璇，高子舒

（哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001）

随着反潜作战要求的不断提高，对跨介质鱼雷的需求也逐渐增大。这些武器均需经历入水阶段，由空气入水的瞬间，流体密度增大800 倍，巨大的冲击载荷极易对雷体结构造成损坏，因此对入水过程进行研究十分必要[1-3]。

入水过程一直以来都受到广泛关注，早期学者们主要采用简单实验或理论方法进行研究，Worthington等[4]首次拍摄到了球体入水的水花溅落和空泡形成过程，被称为入水实验第一人。von Karman[5]首次提出用附加质量法计算入水问题。Wagner[6]在von Karman 研究[5]的基础上更深一步考虑了水面上升现象，得到了结构物沾湿面上的压力分布，为入水问题研究奠定了理论基础。20 世纪70 年代后，学者们在理论研究中更多地考虑了流场特性，Eroshin 等[7]在入水计算时考虑了流体的可压缩性，Howison 等[8]在研究中考虑了气垫效应，并计算了楔形体的入水过程。近年来，随着测试技术的提高，越来越多的学者通过实验观测到复杂航行体的入水过程，张伟等[9]和郭子涛等[10]利用高速相机记录了不同头型导弹在35～160 m/s 入水时的弹道轨迹和空泡形状。黄振贵等[11]拍摄了90°锥头弹丸低速入水的空泡闭合方式和演变过程。侯宇等[12]开展了超空泡射弹小角度入水实验，得到了弹道轨迹、喷溅演变和水下压力波传播特征。

实验方法在观测流场演变和航行弹道方面具有优势，但在研究构型复杂的大尺寸航行器结构的受力时，数值模拟方法更有优势。Oger 等[13]基于光滑粒子流体动力学（smoothed particle hydrodynamics,SPH）方法模拟了楔形体入水过程，得到了结构物表面的压力分布。Iranmanesh 等[14]基于流体体积（volume of fluid, VOF）函数建立了圆柱体水平入水的三维数值模型，得到了圆柱体直径、长度和密度改变对入水深度的影响。Chaudhry 等[15]采用任意拉格朗日-欧拉（arbitrary Lagrangian-Eulerian, ALE）算法和罚函数耦合法模拟了导弹高速入水过程，并与SPH 方法得到的结果进行比较，证明了ALE 方法可以精确模拟入水且更节约资源。此外，多位学者利用ALE 方法研究了不同类型导弹的入水过程，均取得了较好的结果，黄志刚等[16]模拟了不同壁厚的回转体以100 m/s 高速入水的过程，指出头部厚度对回转体的结构强度有重要影响。孙玉松等[17]分析了入水角改变对弹道稳定性的影响，指出在一定范围内，入水角越大，越有利于弹道稳定。汪振等[18]模拟了大口径弹体以不同运动参数入水的过程，得到了弹体载荷变化规律，汪振等[19]还探究了流固耦合参数设置及网格大小对数值模拟结果的影响，并得到了适合大口径弹体入水模拟的参数。在材料模型选取上，Shi 等[20]对比了弹性和刚性航行器在不同参数下的入水特性，指出水弹性效应会使2 种材料的航行体呈现出不同的加速度、应力和结构变形特性。贾鹏[21]探究了入水状态对航行体运动和受力的影响，通过比较3 种材料模型，发现在整体计算准确性上，塑性本构模型优于弹性本构模型和刚性本构模型。

关于入水问题的研究已有成熟体系，但采用的航行体模型多为实心体或完整壳体，实际上，跨介质鱼雷由自导段、战雷段、推进段和尾段构成，并利用连接件将多个舱段装配起来，李刚[22]基于LSDYNA 软件研究了装配式导弹在垂直入水时的载荷分布，指出弹体与环箍连接处由于形态发生改变，冲击作用产生的应力易集中于此，使其相对其他部位更加脆弱，在弹体结构设计时应重点考虑。若仅以整体形式研究，除关注头部瞬间大冲击外，难以观察到舱段间的相互作用规律，因此需要针对舱段连接部位的受力特性以及壳体间相互影响规律展开深入研究。

本文中，参考MK46 型鱼雷结构展开数值模拟研究，重点关注鱼雷撞水时各舱段壳体及连接件处的响应特性。基于LS-DYNA 平台中的ALE 算法，对平头、球头、钝头和尖头4 种头型鱼雷分别进行垂直入水模拟，使用工程上较常见的楔环与卡箍作为连接件组装舱段，这2 种连接件质量轻，在连接稳定性与装卸方面也都更具优势[23]。

1 数值方法和几何模型

1.1 流固耦合ALE 算法

当流体与结构共同构成的体系受到动载荷时，流体与固体之间发生相互作用，这就是流固耦合问题，LS-DYNA 中的ALE 算法将欧拉网格与拉格朗日网格相结合，可以有效地解决此类问题[24]。在ALE 算法中，流体域采用欧拉方法，使网格在空间中保持静止，结构采用拉格朗日方法，使网格能随物体运动，将静止的欧拉坐标系视为参考系，则需满足的控制方程有质量守恒方程、动量守恒方程以及能量守恒方程[25]：

式中：ρ 为流体密度；t为时间；x为欧拉坐标；vi为流体的速度；wi为相对速度，wi=vi–ui，ui为固体的速度；E为能量；fi为作用于流体的体积力；σij为应力张量，下标i、j在张量中分别表示不同的方向。σij的表达式为：

式中：p为压力；µ为动力黏度；δij为克罗内克函数，当i=j时，δij=1，当i≠j时，δij=0。

1.2 罚函数法

LS-DYNA 为接触面提供了罚函数法来计算耦合关系，其原理为，当运动过程中预测到接触面上从节点与主表面之间会发生穿透时，会在二者之间引入一个较大的界面力F：

式中：k为接触界面刚度，d为穿透量。实际上，式(5)的物理意义相当于在从节点与被穿透主表面之间放置一个法向弹簧以限制从节点对主表面的穿透，k则相当于弹簧的刚度：

式中：K为耦合中涉及流体单元的体积模量；V为包含主流体节点的流体单元的体积；A为连接在从节点上固体单元的平均面积；ψ 为避免数值模拟不稳定性引入的缩放因子，设置为0.1[25]。

1.3 连接结构模型

综合工程中的使用效果以及安装的便捷性，选择楔环和卡箍来装配壳体，不考虑固定螺钉等复杂结构，仅研究壳体与连接件之间相互拉压作用的影响[26]。连接处的尺寸设计直接决定连接的稳定性，因此，为提高承载能力，参考黄鹏等[27]和宋保维等[28]的研究，本文中确定了连接结构的造型，如图1 所示。

图1 连接件结构Fig.1 Geometries of the connectors

1.4 鱼雷头部曲线及各舱段参数

鱼雷头部形态对运动受力和弹道轨迹具有决定性作用，平端头和弧形头在工程中最常见。弧形头鱼雷在水下具有更好的流线型，运动时受阻力更小；平端头鱼雷在水下有更好的弹道稳定性，且便于导引装置安装[10]。因此，参考文献[29]，选取4 种头型分别研究弧形头和平端头鱼雷在垂直入水工况下的结构响应特性，参考MK46 型鱼雷进行建模，具体参数如图2～3 所示，其中鱼雷总质量为230 kg[30]。

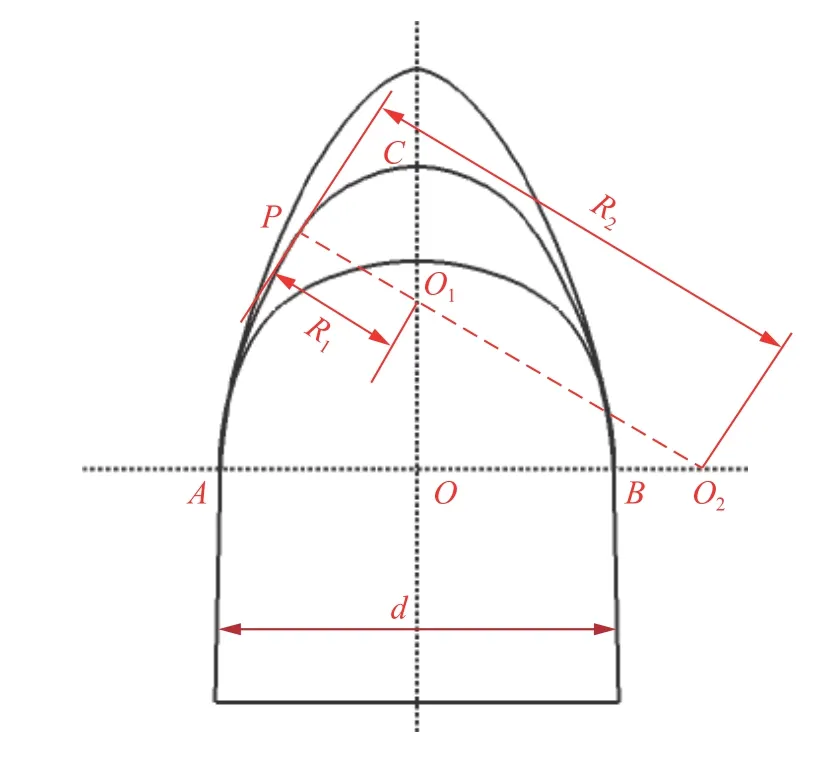
图2 弧形头结构尺寸Fig.2 Dimensions of the head shape

图3 鱼雷结构Fig.3 Geometry models of torpedoes

鱼雷1～3 为弧形头鱼雷，∠OO1O2为45°，R1分别为60、140 和200 mm；鱼雷4为平端头鱼雷，无弧形部分；鱼雷5 为平头型整体式鱼雷，用于对比研究。鱼雷结构按照有限元通用简化原则处理，只研究主体结构，忽略圆角、定位孔等对分析结果影响较小的局部复杂结构，通过固定连接接触代替壳体中的螺钉和螺纹孔等。外部壳体、连接件和内部载重均以此方式建模，并利用连接件装配成型。为方便研究，按照自头至尾的顺序，分别命名壳体为K1～K4、楔环为X1～X3、卡箍为G1～G3、内载重为Z1～Z4，其结构分解如图4 所示。通过调整连接件插入位置及内载重质量，使所有鱼雷除头部曲线不同外，各舱段的长度、直径及质量均保持一致。

图4 弹体装配情况Fig.4 Structural assembly of a torpedo

2 计算模型和验证

2.1 计算设置

由于鱼雷模型为回转体且数值模拟具有对称性，为节约计算资源，采用1/2 模型，将中间面设置为对称边界。重点关注结构物的响应特性，不关心流场空泡等特性。因此，为保证计算精度的同时节约计算资源，建立如图5 所示的流场，采用了无反射边界条件，即认为流场域边界无限大，则边界处的反射波不会对内部计算域产生影响。

图5 计算边界条件Fig.5 Computational domain and boundary conditions

鱼雷壳体厚度为10 mm，材料采用航天工业中常用的7075 铝合金，强度高且耐腐蚀；连接件材料为LC4 铝合金，亦称超硬铝，制备工艺成熟，使用广泛，是一种耐腐蚀、性能好的合金材料。壳体与连接件的铝合金材料均采用弹塑性本构模型，2 种材料参数分别来自于文献[31-32]，如表1 所示。在LSDYNA 中选择*MAT_PLASTIC_KINEMATIC 关键字定义，既可以很好地模拟金属材料弹性阶段变形，在达到屈服应力后还可以模拟材料的塑性变形。

表1 铝合金材料参数Table 1 Material parameters of aluminum alloy

流场材料参数来自文献[33]，选择*MAT_NULL 关键字定义，采用*EOS_GRÜNEISEN 状态方程模拟水的运动：

式中：pw为水的压力，Ew为水的体积内能，c为水中声速，γ0为Grüneisen 常数，b为γ0的一次体积修正系数，S1～S3为状态方程的系数，ηw由水的相对体积Vw计算得到。取水的密度为1 000 kg/m3，Ew=289.5 kPa，c=1 480 m/s，S1=1.921，S2=–0.096，S3=0，γ0=0.35，水的初始相对体积为1。

采用*EOS_LINEAR_POLYNOMIAL 状态方程模拟空气的运动：

式中：pa为空气压力，C0～C6为多项式系数，Ea为空气单位体积内能，ηa由空气的相对体积Va计算得到。取空气的密度为1.25 kg/m3，Ea=253.3 kPa，C0=C1=C2=C3=0，C4=C5=0.4，C6=0，取空气的初始相对体积为1。

2.2 网格无关性验证

网格尺寸的选取对提升数值模拟精度和效率具有十分重要的影响，以鱼雷4 为例，采用楔环连接方式，通过无关性验证来确定最优网格尺寸。固体网格分别选取6、4、2 和1 mm 等4 种尺寸，这时流场网格尺寸为10 mm；流体域网格分别选取12、10、8、6 和5 mm 等5 种尺寸，这时鱼雷网格尺寸为2 mm。监测了壳体冲击最大加速度amax和中心水单元冲击最大压强pmax，验证结果见表2。

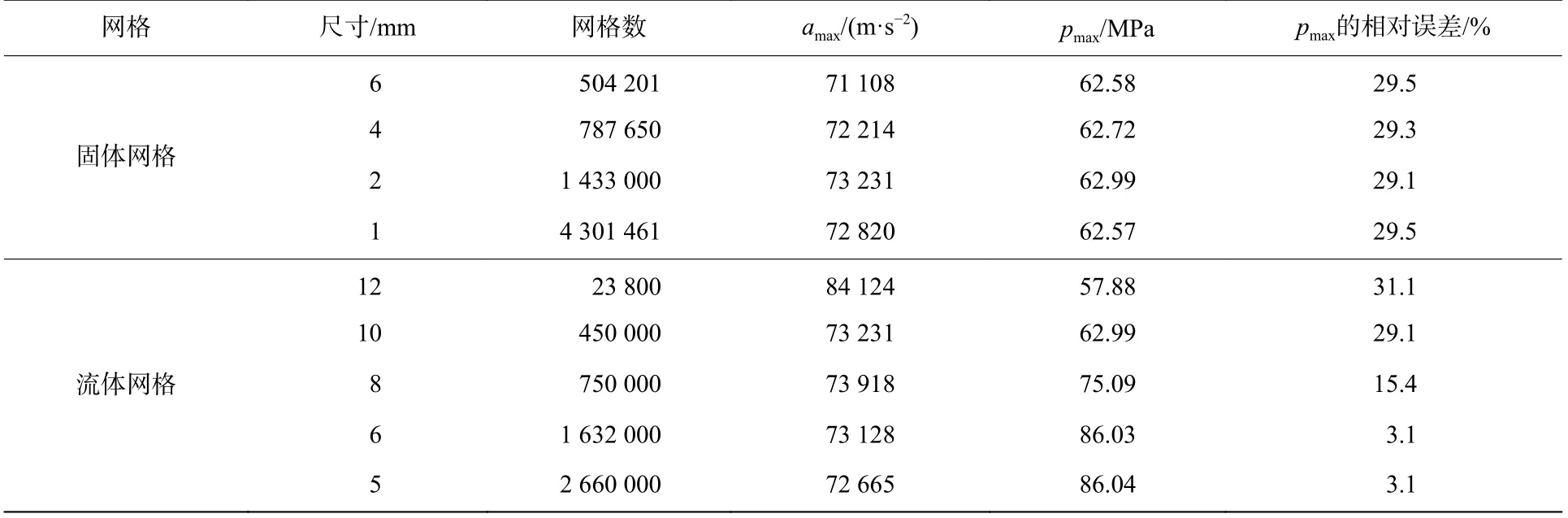
表2 网格无关性验证结果Table 2 Results of mesh independence verification

由表2 可知，仅改变固体网格尺寸，基本不会对监测参数产生影响，但尺寸越大，网格单元的结果越粗糙，综合考虑，固体网格尺寸选取为2 mm。流体域网格尺寸改变会对压强及雷体加速度产生影响，比较发现，6 和5 mm 的2 套流体网格计算结果几乎无差别，因此流体网格尺寸选取为6 mm。

2.3 数值模型合理性验证

为验证数值模型的合理性，模拟了平头鱼雷的入水过程，并与现有的实验结果[34]进行比较，结构物及计算域尺寸如图6 所示，入水过程的空泡图像如图7 所示。图7(c)给出了数值模拟得到的空泡与实验结果的对比，可以观察到，数值模拟得到的对应时刻的空泡形成及发展特点与实验结果吻合，水箱中由于空化作用出现大量气泡，这与本文中关注的结构物受力特性无关。综合来看，认为数值模型是合理的。

图6 实验装置示意图Fig.6 Schematic diagram of the experimental configuration

图7 入水过程空泡形态Fig.7 Cavity shapes during water entry

依据von Karman 一元碰撞理论，得到平板撞击水面的压力峰值公式为[35]：

式中：水的密度ρw=1 000 kg/m3，水中声速c=1 480 m/s，当入水角 φ =90°，垂直入水速度v⊥=60 m/s 时，计算得到的理论最大冲击压力为88.8 MPa，将此值与2.2 节数值模拟得到的中心水单元冲击最大压强pmax进行对比，相对误差见表2。可以得到，当网格尺寸合理时，模拟得到的结果与理论值的相对误差仅为3.1%，进一步验证了数值模型的合理性。

3 结果分析

3.1 运动分析

分别对图3 中的5 种鱼雷模型以60 m/s 速度垂直入水的工况进行模拟，其中鱼雷1～鱼雷4 为多舱段式鱼雷，研究了楔环和卡箍2 种连接方式，将整体式鱼雷5 作为对比。4 种头型鱼雷的入水过程如图8所示。由图8 可知，由于撞水瞬间极快，冲击作用会使鱼雷头部端面变形，其中平端头鱼雷最明显。在研究的3.00 ms 内，所有头型鱼雷的弹道均保持稳定，随着雷体深入，周围液面高度上升，产生的水花沿壳体边缘向上扩散。本文中主要研究鱼雷垂直撞水后短时间内的结构响应，当运动方向无偏转趋势时，雷体受力主要沿x轴方向，其他方向作用力的量级很小，可忽略不计。

图8 鱼雷入水过程Fig.8 Water-entry processes of the torpedoes

图9 给出了鱼雷4 壳体沿x方向的加速度变化曲线，可用于衡量结构物受合力大小。由图9 可知，各舱段的加速度变化规律并不相同，撞水前，壳体以整体形式下降，各舱段均保持匀速前进。鱼雷撞击水面后，头部壳体加速度快速达到峰值，此时后面壳体仍保持初始状态前进。随着时间的推移，后3 段壳体加速度依次变化，且位置越向后，加速度开始波动的时间也越晚，舱段距离越长，间隔的时间也越长，这反映了冲击造成的壳体响应是以波的形式进行传递。整体来看，壳体加速度均在波动中趋于稳定，分段壳体间响应的差距逐渐减小，这是由于壳体自身的震动以及连接件的相互作用产生了能量的耗散，减弱了冲击力的传递。

图9 鱼雷4 壳体沿x 方向的加速度Fig.9 Shell acceleration in the x direction of torpedo 4

根据对平头鱼雷的研究发现，不同连接方式的壳体所受冲击载荷基本为同一量级且主要变化规律一致，因此任选其一，导出卡箍连接方式的鱼雷1～3 壳体以及整体式鱼雷5 的x方向加速度随时间的变化曲线进行对比，如图10 所示。可以发现，鱼雷在撞击水面后，加速度均会瞬间升高，而后在波动中逐渐减缓，头型越尖的鱼雷所受加速度越小，说明它所受的瞬间抨击越小。

图10 壳体x 方向加速度随时间的变化Fig.10 Time evolution of acceleration in the x direction for shells

平头鱼雷的第1 个加速度峰即为最大值，但弧形头鱼雷的最大冲击峰出现较晚，这是因为平头鱼雷入水类似于平板抨击水面，撞水瞬间即有较大面积与水接触，随后与水的冲击效应减弱，因此第1 个冲击峰即达到最大加速度。弧形头具有更好的流线型，撞水时雷体与水平面仅相切于一点，随后触水面积逐渐增大，与水抨击产生的冲击波会在传递过程中不断叠加，同时冲击作用产生的能量还会逐渐转化及耗散。综合能量的叠加与耗散，壳体的加速度响应会先升高再逐渐趋缓，因此弧形头壳体的最大冲击峰一般出现在第2 个或第3 个加速度峰。

对比图9 与10(d)可以发现，鱼雷5 的加速度在撞水瞬间迅速达到峰值，随后瞬间降低，几乎不再产生波动并逐渐趋于零，加速度恒指向运动的负方向。但鱼雷4 各舱段的加速度会围绕零值在正负方向上有几乎同等量级的持续震荡，这说明实际每一舱段所受的力并非恒定沿某一方向，而是在反复变向，因此雷体受阻力后并非持续降速，而是会受到后段的撞击作用而加速，相邻壳体间会来回碰撞，连接件也被反复拉压。

鱼雷4 和5 以同样运动状态撞水时所受到的水面阻力相同，但鱼雷5 的最大加速度远小于鱼雷4 的壳体K1 的最大加速度，这是由于整体式鱼雷的加速度是将受到的水面阻力除以整体质量，不考虑自身前后段间的内力；而分段鱼雷的各舱段是相互独立的部件，则壳体K1 加速度是将其受到的力除以这一段的质量。当撞水产生的冲击波刚刚作用到壳体K1 时，存在极短的时间间隔，响应相对滞后的后部结构尚未对其产生作用力，这一瞬间壳体K1 承受抨击水面的全部冲击，从而产生一个极高的加速度峰值。但随着结构依次响应，后一舱段也会对前一舱段作用，则加速度也会随力的作用而波动。

实际上，每一舱段受到冲击后响应的开始时间及大小并不相同，前段壳体会长时间处于较高水平的抨击震荡状态中，而后段壳体的加速度变化相对小很多。若仅以整体形式研究，将难以观察到每一结构单独的运动规律，也易忽略连接处的受力。

3.2 材料结构应力分析

撞水后短时间内，所有头型的鱼雷均保持稳定垂直深入，相较之下，平端头鱼雷所受冲击最大，当弹道无偏转趋势时，其连接结构承受的冲击载荷也最大，因此后续主要针对鱼雷4 的结果展开深入研究。冲击波产生的力在结构中体现为应力的作用，材料所承受的应力大小是判断其是否损坏的根本性因素。本文中，以von Mises 屈服准则作为材料是否发生屈服的判据，即采用范式等效应力进行分析。

图11 为鱼雷4 分别采用楔环和卡箍连接方式时的应力云图，结合图9 可以发现，在0.24 ms 时，壳体K2 加速度刚好开始波动，而应力也恰好在此时发生变化，随着入水进行，鱼雷不断抨击水介质单元，头部所受的力以波的形式逐渐向后传递，后部结构的加速度也依次开始改变。加速度是由作用于其上的力引起的，也正因如此，各部件的加速度会根据力的作用方向围绕零值在正负半轴上波动。

图11 鱼雷4 不同时刻的应力云图Fig.11 Time evolution of stress contour for torpedo 4

2 种连接形式的鱼雷各结构最大应力随时间的变化曲线如图12 所示，头部壳体最先撞击水面，也最危险，其最大应力在多个时刻超过了屈服极限，之后材料开始产生塑性形变，在此阶段，材料的变形量增加，但应力不再发生变化，因此应力曲线中最高只能显示至455 MPa。后段壳体的最大应力也处于较高量级，甚至在几个时刻达到屈服极限，说明当鱼雷处于更加恶劣工况或壳体厚度降低时极易发生损坏，这是十分危险的。

图12 鱼雷4 最大应力随时间的变化曲线Fig.12 Time evolution of maximum effective stress for torpedo 4

应力波向后传递时会在壳体边缘停滞，结合图11 可以明显观察到应力集中。连接处的壳体应力普遍高于其周围壳体，甚至某些时刻约为其周围材料的1 000 倍。X1 应力在0.36 ms 达到最大峰值，而X2、X3 应力均是在入水较后期达到更高水平，并分别于2.21 和2.36 ms 达到最大应力峰值，接近材料的屈服极限。卡箍的最大应力出现在2.03 ms，此时卡箍2 接近材料的屈服极限。

连接件承受最大应力时的状态见图13，连接件周围壳体由于受到拉伸影响，产生了非常明显的形变。楔环在挤压作用下位置发生改变，壳体间出现较大缝隙，两侧受力面的应力远高于其他单元；卡箍也被拉伸变形，其中间凹槽应力水平高于其他位置，受力截面上的单元也几乎达到材料的屈服极限。

图13 在最大应力时连接件的变形情况Fig.13 Deformation of the connectors at the maximum stress

3.3 连接部位接触面受力分析

连接件处的受力情况反映了其连接的壳体间的相互作用关系，楔环与卡箍连接均属于典型的面-面接触，对于非固定连接，面与面之间只能体现为接触面上的挤压作用。当壳体之间相互靠近时，会相互挤压，同时也会挤压连接件，但当壳体之间相互远离时，并不能产生拉力，而是体现为壳体对连接件的压力。

接触面间力的关系如图14 所示。当前后壳体挤压时，由于楔环装配时留有空隙，因此前部壳体不会对其有指向鱼雷尾部的力，同样后部壳体不会对其有指向头部方向的力。而卡箍被嵌在壳体的凹槽之中，前后壳体均会对其有正反方向的挤压。当前后壳体远离时，为防止脱钩，连接件会与接触面挤压，由于力矩作用，楔环会向外转动，其周围壳体分别向内外翻出；卡箍也被掰弯变形，其周围壳体均向内翻。显然，拉伸作用对鱼雷的危害大于挤压作用，当舱段间相互挤压时，前后壳体及连接件之间接触更加严密，但拉伸状态下舱段间相互远离，壳体与连接件形状改变，原本贴合处产生缝隙。这种趋势会减弱连接稳定性，恶劣工况下甚至会破损、脱钩，海水等其他杂物也易渗入装置内部。

图14 接触面受力关系Fig.14 Forces on contact surfaces

雷体轴向沿x方向，头部指向负半轴，则分析x方向的力能够判断各部件间力的作用情况。图15 给出了各壳体与连接件之间的力随时间的变化曲线，选取的数据均为接触面上靠后段结构的受力值。根据牛顿第三定律，另一面上的作用力与图15 中数值大小相同方向相反。

图15 鱼雷4 连接接触面上的力随时间的变化Fig.15 Time evolution of contact surface forces of torpedo 4

壳体间在撞水前相对静止，从接触水面开始，壳体间受力发生改变。前期壳体间挤压作用明显，撞水瞬间，前部壳体产生骤停趋势，而后部舱段仍保持撞水前的运动状态，挤压前面舱段，这在壳体K1 与K2 的接触面上体现最明显。这是由于头部壳体最先接触水面，冲击作用的影响最大，同时后部所有载荷都保持初始前进状态，质量大，惯性大，所有惯性作用产生的力均施加在此接触面上。约1.7 ms 后，壳体间的力有较长时间为零，说明此时相邻壳体分离，同时正挤压中间连接件。

连接件内嵌于壳体间，受两侧壳体力的大小相等方向相反。对比3 个连接处发现，越靠后的结构，力作用曲线开始波动时间越晚，连接件受力最大值出现时间也越晚。综合来看，当连接件受力达到最大时，壳体正相互远离，结合图12 的应力变化曲线可知，此时材料应力已接近屈服极限。因此壳体间相互远离时，不仅会产生缝隙、降低连接效果，而且对连接件的拉拽作用还易造成材料损坏。

4 结 论

利用数值方法研究了跨介质鱼雷以60 m/s 的速度垂直入水时各舱段及连接件的轴向加速度响应和受力特性，建模参考了MK46 型鱼雷的构型，探究了不同连接方式和多种头型对鱼雷入水的影响，并与整体式鱼雷进行了对比，得到以下结论。

(1) 鱼雷撞水后受到瞬间的大冲击影响，头部壳体由于直接接触水面迅速达到加速度峰值。短时间内鱼雷的弹道稳定，则头型越尖受轴向冲击作用的影响就越小，平头鱼雷受到的冲击最大，且其头部壳体在多个时刻达到了材料的屈服极限。

(2) 由于应力以波的形式向后传递，鱼雷各舱段受冲击后会按照距离头部的位置依次响应，且应力波会随着能量的不断转化及耗散逐渐减小，因此前段壳体所受的影响高于后段壳体。

(3) 连接处会产生应力集中，安装的位置和连接件形状易发生改变，相对其他部分更脆弱。连接部位的壳体所受应力是其余部位的1 000 倍，仅次于头部壳体，最高时甚至超过材料的屈服极限。

(4) 壳体间并非保持相对静止，而是在来回碰撞并不断拉压连接件。后段壳体在撞水初期对前部有明显的挤压作用，但在后期又相互远离，这会对连接件产生明显的拉伸作用，接触面上的力达到最大，连接件受到的应力也在此时达到屈服极限，这是十分危险的，极易导致工作故障。

除头部壳体外，连接部位也是易产生高应力、大变形的区域，同时壳体间远离时对连接的破坏明显大于压缩，因此设计中应针对这一特点进行优化，如增加密封圈或固定装置等以保证鱼雷正常工作。