爆炸载荷下陶瓷颗粒增强聚氨酯复合材料动态响应数值分析*

邹广平，梁 正，吴松阳，唱忠良

（哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001）

聚氨酯（polyurethane, PU）弹性体因其优良的吸能减振防护性能，常在军事、航空航天等领域用作防爆抗冲击材料。但随着科技的发展，对PU 的抗压抗冲击性能也有了更高的要求，已知提高聚合物材料性能的一种有效的方式是以聚合物为基体，添加增强相制备复合材料[1-5]。陶瓷作为一种无机刚性填料具有高硬度、高强度、低密度的特点，是提高复合材料抗压和抗冲击性能的良好增强相。胡勤等[6]通过不同尺寸燃烧弹侵彻6061 铝合金约束直径为6 mm 的Al2O3陶瓷球复合材料实验与数值模拟，从靶板损伤以及吸能方面分析了陶瓷球提高复合材料抗弹性能的原因。郑伟峰等[7]对颗粒Al2O3增强环氧树脂复合材料进行了力学性能测试，发现加入颗粒Al2O3提高了体系的玻璃化转变温度，拉伸和弯曲模量随着添加量的增加而增大，分析其破坏横截面，表明颗粒Al2O3阻止了微裂纹扩展，有效提高了体系的力学性能。邹广平等[8]利用霍普金森杆对陶瓷球增强聚氨酯复合材料进行了动态冲击实验与数值模拟研究，发现其抗冲击性能随陶瓷球尺寸的减小而增强。Zhou 等[9]制备了Al2O3颗粒增强聚氨酯基复合材料，研究了Al2O3含量和不同硅烷偶联剂对复合材料力学性能和冲蚀磨损性能的影响。发现复合材料的拉伸强度和断裂伸长率均随颗粒含量的增加而降低。Ouyang 等[10]制备了添加纳米Al2O3陶瓷微球的聚氨酯基复合材料，并利用分离式霍普金森压杆研究了其抗压性能，结果表明复合材料的动态冲击能量吸收相比纯聚氨酯增加了约15%。

目前，关于颗粒增强复合材料的研究集中在金属基以及纳米和微米尺度，并且主要研究其静动态压缩、拉伸、侵彻以及抗磨损性能，针对毫米级陶瓷球增强聚氨酯在爆炸载荷下的研究很少。本文中基于有限元模拟方法，对毫米级Al2O3陶瓷球增强的聚氨酯基复合材料进行小当量爆炸载荷下的动态响应研究，并探究爆炸当量和陶瓷球尺寸对复合材料板变形、吸能等方面的影响。

1 数值模型

任意拉格朗日-欧拉（arbitrary Lagrangian-Eulerian，ALE）算法广泛应用于流固耦合和大变形问题分析中，其不仅克服了Euler 网格在处理多材料相互作用或者移动边界时的困难，还解决了Lagrange 网格大变形问题，完美结合了二者的特性，所以使用ALE 算法可以很好地模拟爆炸过程[11]。LS-DYNA 基于显式数值方法，非常适合用于分析爆炸波传播相关的动态问题。同时作为经典的动力学计算软件，其ALE 算法也较为完善，因此采用LS-DYNA 来进行爆炸载荷下复合材料的动态响应数值分析。

使用关键词MULTI_MATERIAL_GROUP 控制的多物质ALE 流固耦合算法，建立复合材料在空气中的数值模型，如图1 所示，建模时使用g-cm-µs 单位制。由于近距离爆炸的冲击波为高频波，需要较细密的空气网格才能反映出完整的冲击波特性[12]，因此空气采用尺寸为1 mm 的Euler 网格，但细密的网格会增加计算负担，考虑到复合材料结构的对称性，采用1/2 建模的方式以加快计算速度，在对称面施加对称约束，并在空气域四周施加非反射约束，来模拟无限大空域中爆炸波传递。聚氨酯和Al2O3陶瓷球部分采用Lagrange 网格，网格尺寸为0.6 mm。将密度为1.59 g/cm3的球形TNT 炸药通过关键词VOLUME_FRACTION_GEOMETRY 放置到空气网格中，爆距R为80 mm，爆炸当量选定3 g（即爆炸半径为7.7 mm），起爆时间通过关键词INITIAL_DETONATION 控制。

图1 ALE 有限元模型Fig.1 ALE finite element model

陶瓷颗粒增强聚氨酯复合材料尺寸及陶瓷球排布如图2 所示，将直径为4.5 mm 的Al2O3陶瓷小球交叉排列，尽可能填满长宽均为120 mm 的长方体聚氨酯弹性体，陶瓷球共495 个。在聚氨酯四周施加固定约束。

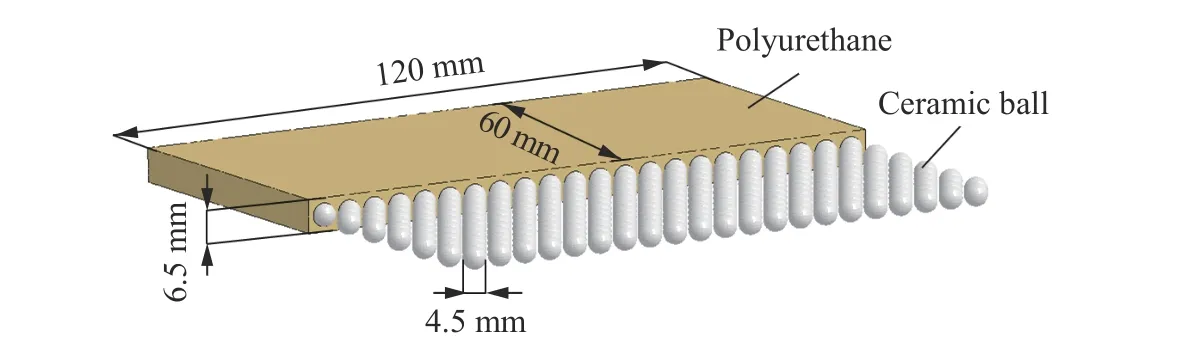
图2 陶瓷颗粒聚氨酯复合材料有限元模型Fig.2 A finite element model of ceramic particle polyurethane composites

2 材料模型

空气可理想化视为理想气体，此时气体分子不占任何体积，彼此之间不存在相互作用力，气体压力可表示为密度与内能乘积的线性函数，在LS-DYNA 使用NULL 材料模型来表示无黏性理想气体，理想气体状态方程表达式为：

式中：pa为空气压力；γ 为绝热系数，取1.4；ρ0为空气初始密度，标准大气压下取1.225 kg/m3；E为初始比内能，取2.5×105J/m3。

使用HIGH_EXPLOSIVE_BURN 材料模型以及JWL 状态方程来描述TNT，表达式为：

式中：p为爆炸冲击波压力，e0为初始比内能，A、B、R1、R2、ω 为状态方程参数，V为炸药相对体积，定义为起爆过程开始时爆炸产物密度与炸药密度的比。TNT 材料具体参数如表1 所示。

表1 TNT 炸药材料参数[10]Table 1 Material parameters of TNT explosive[10]

陶瓷作为高抗压的脆性材料，在受到冲击后会产生渐进性破裂损伤。Johnson-Holmquist 本构模型(Johnson-Holmquist Ⅱ, JH-Ⅱ)动态本构模型含有强度模型和损伤演化参数[13]，可以描述脆性材料在大变形、高应变率以及高压下的强度，考虑损伤劣势效应，即认为材料软化是通过损伤积累而逐渐出现。JH-Ⅱ动态本构模型被广泛适用于高应变率高压下陶瓷、岩石等脆性材料的模拟，Al2O3陶瓷球的JH-Ⅱ本构材料参数见表2，对应关键词为JOHNSON_HOLMQUIST_CERAMICS。

表2 陶瓷球材料参数Table 2 Ceramic ball material parameters

超弹性材料在小变形范围内符合胡克定律，但在大变形时其应力-应变关系呈高度非线性，目前有多种超弹性本构模型，例如基于热力学统计理论的Arruda-Boyce 模型[14]以及基于连续介质力学的Rivlin 模型。大部分超弹性本构都可以用以应变张量不变量I1、I2和I3表示的应变能函数β 来表述。类橡胶材料可以看作是不可压缩的，因此其中应用最多、最经典的是Rivlin 模型[15]，许多其他经典的超弹性材料本构模型都是由此演变而来的，其广义多项式为：

式中：Cij为材料常数，Di为材料参数，表示材料的可压缩性，J为材料变形前后的体积比，通常情况下将聚氨酯视为不可压缩材料，即变形前后体积不变，因此J=1。工程应用较多的是简化后的三项模型，其表达式为：

Zou 等[16]通过实验得到聚氨酯弹性体的应力-应变曲线，通过上式拟合得到材料参数C10=1.11×10−4，C01=1.74×10−4，C20=3.134×10−5。

3 数值结果分析

3.1 数值模拟

炸药从起爆点先压缩并提高反应区的温度随后以炸药的燃烧速度从起爆点向外开始膨胀并产生高压冲击波迅速传播，LS-DYNA 可以用状态方程来定义炸药的体积膨胀，图3 可以反映出炸药反应区产生高压的瞬态分布。

图3 爆炸起始点波的传递Fig.3 Wave propagation at the starting point of explosion

TNT 爆炸产生的波阵面首先在空气中以理想自由场方式传播，如图4 所示，在接触复合材料表面后其速度降为零，并积累形成高压区，从而产生压力高于入射冲击波的反射波，其中波阵面即入射波与复合材料表面夹角为α。爆心正下方的反射波为正反射(α=0°)，随着α 的增大，产生规则斜反射(α＜α0)，当α 达到临界值α0后，反射波赶上入射波，并汇合形成马赫波(α0＜α＜90°)。

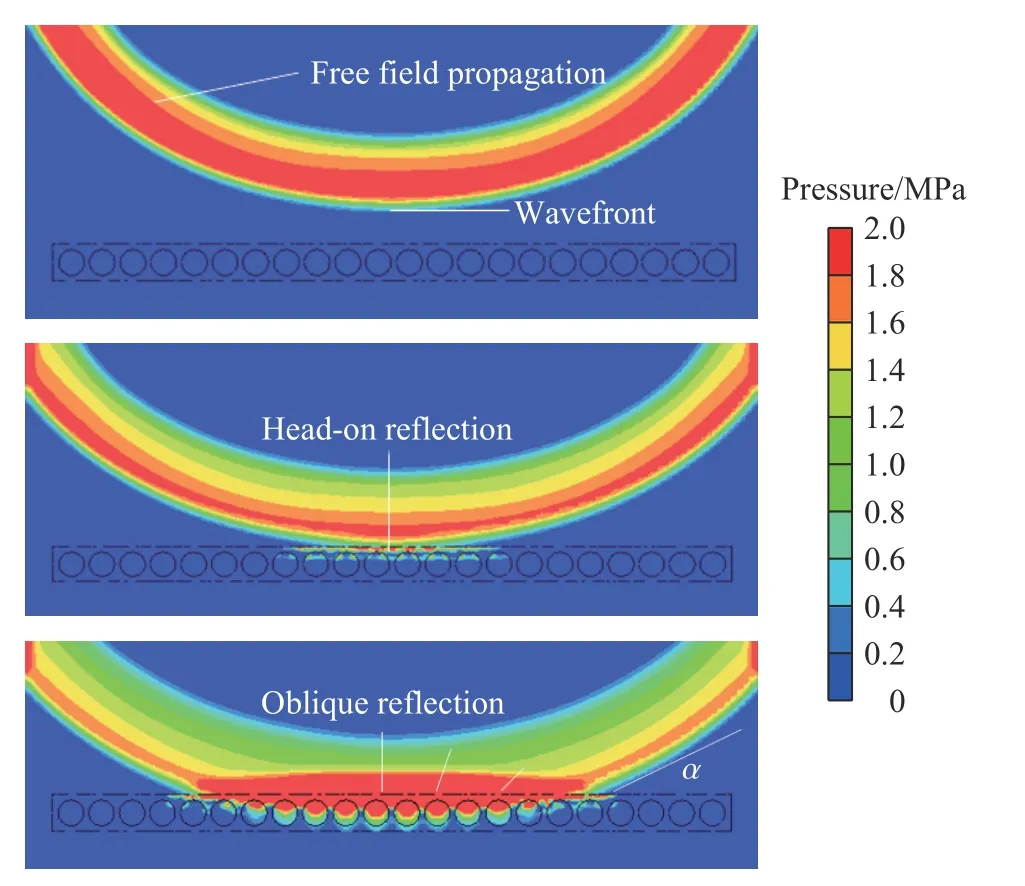
图4 爆炸冲击波的传播与反射Fig.4 Propagation and reflection of blast wave

TNT 爆炸过程中，爆距R=40, 50, 60, 70, 80, 90, 100 mm 处的压力时程曲线，如图5 所示。TNT 炸药起爆后成为高温高压的轰爆产物，并压缩空气产生冲击波，冲击波在到达空气中某点后，该处压力瞬间跃升至最大值，波阵面经过后迅速下降，爆炸冲击波在传播过程中衰减迅速，峰值超压逐渐减小并且传播速度降低。

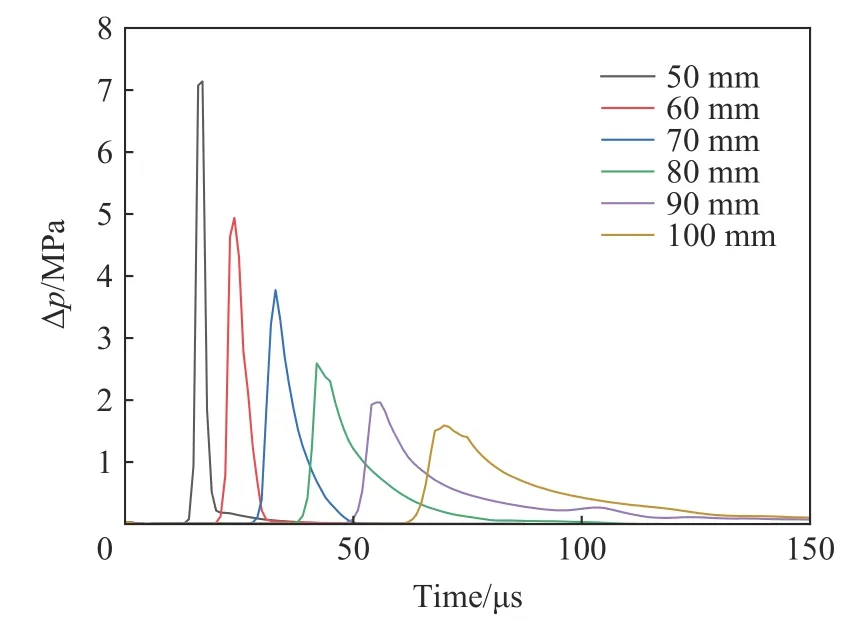
图5 不同爆距压力时程曲线Fig.5 Time histories of pressure at different blasting distances

目前有多种通过大量实验总结的经验公式来表述爆炸峰值超压与爆距关系。其中，较为经典的是Henrych 自由场爆炸超压经验公式[17]：

式中：∆p为爆炸冲击波峰值超压，z为比例距离，W为TNT 质量。由此可以计算出在不同爆距下的最大压力，与数值模拟结果对比曲线如图6 所示。可以看出，随着爆距增大，数值模拟结果与理论值差距越来越小。原因是z越小，经验公式计算所求得的偏差越大。

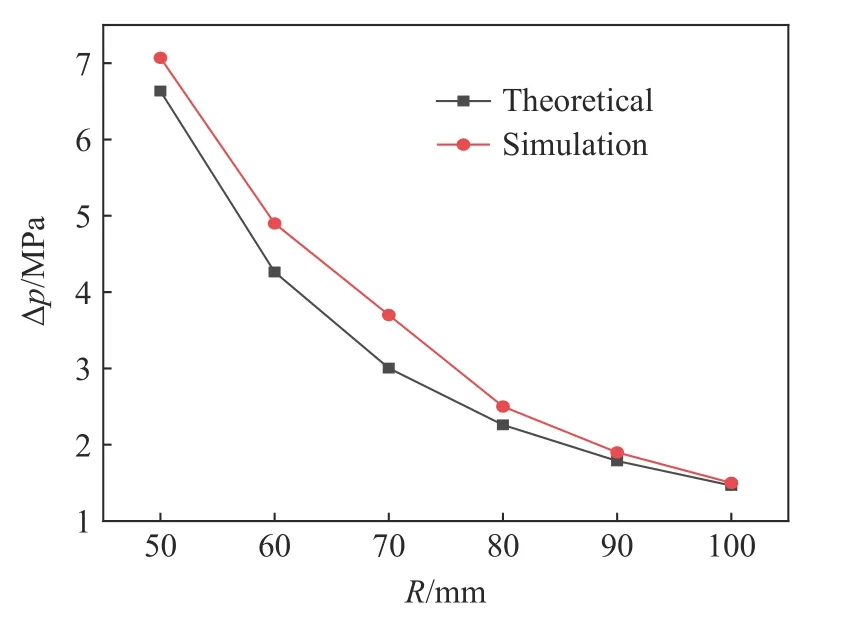
图6 超压的数值模拟与经验公式结果对比Fig.6 Comparison between numerical simulation and empirical formula

为了验证模型的正确性，采用相同的建模方式和材料参数建立如图7 所示的复合材料板侵彻模型，对其进行质量为11 g 的球形弹侵彻的数值模拟，并将结果与实验结果进行对比。不同侵彻速度下，实验和数值模拟得到的剩余速度的对比结果如图8 和表3 所示，二者的误差在可允许范围内，证明该模型下，复合材料板的动力响应与实验较为符合。

表3 剩余速度的数值模拟与实验对比Table 3 Comparison of residual velocity between simulation and experiment

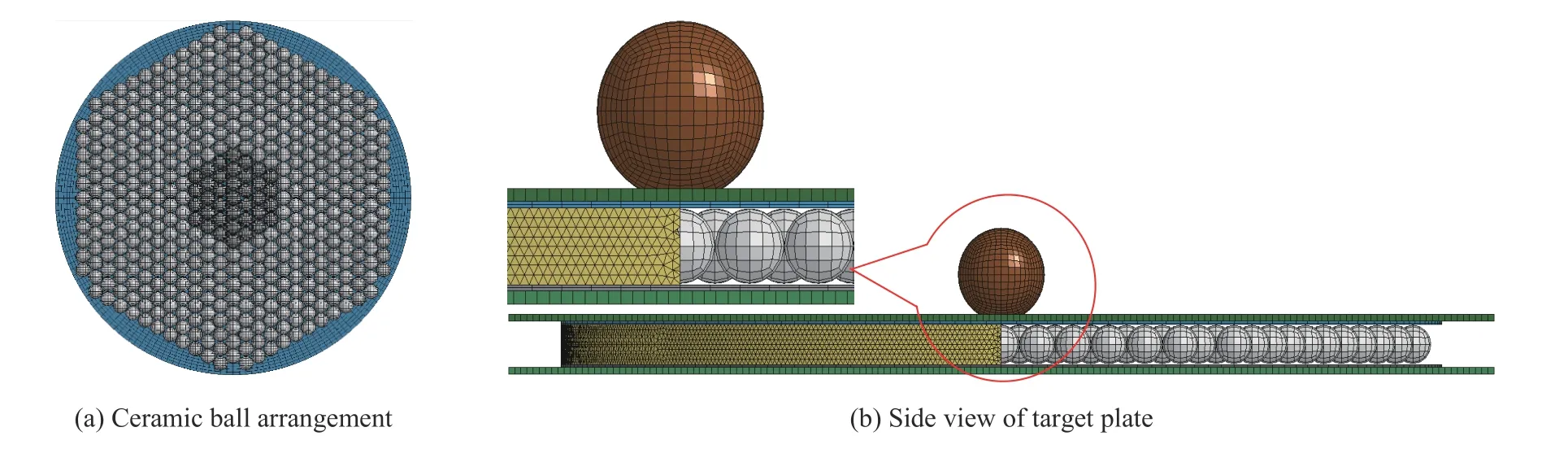
图7 聚氨酯/陶瓷球复合结构模型Fig.7 Polyurethane/ceramic ball composite structure model

图8 数值模拟与实验结果的剖面对比Fig.8 Cross-section comparison of numerical simulation and experimental results

3.2 复合材料动态响应分析

图9 为复合材料背波面上距中心不同距离点Rd的垂直方向位移曲线，爆炸冲击波使得复合材料板产生沙漏状的变形，复合材料中心点在475 µs 时的挠度为7.23 mm，在225～275µs 时间段内，复合材料中心点位移的速度变慢，使得最大挠度不在中心点，而是在距中心点10～15 mm处，分析其原因，爆炸冲击波以压缩波的形式弧形传播，先到达复合材料板的中间点，在130 µs时引起中心点的挠度下降，然后在290 µs 时反射为拉伸波，造成向上的挠度。而此时复合材料板中心点两侧开始受到压缩波的作用，引起向下的挠度，就产生了中间挠度比两侧挠度更高的现象如图10 所示。随着压缩波增大，整个板产生了向下的挠度。

图9 复合材料底部距中心不同距离点的挠度曲线Fig.9 Deflection curves of different distance points from the bottom of composite material to the center

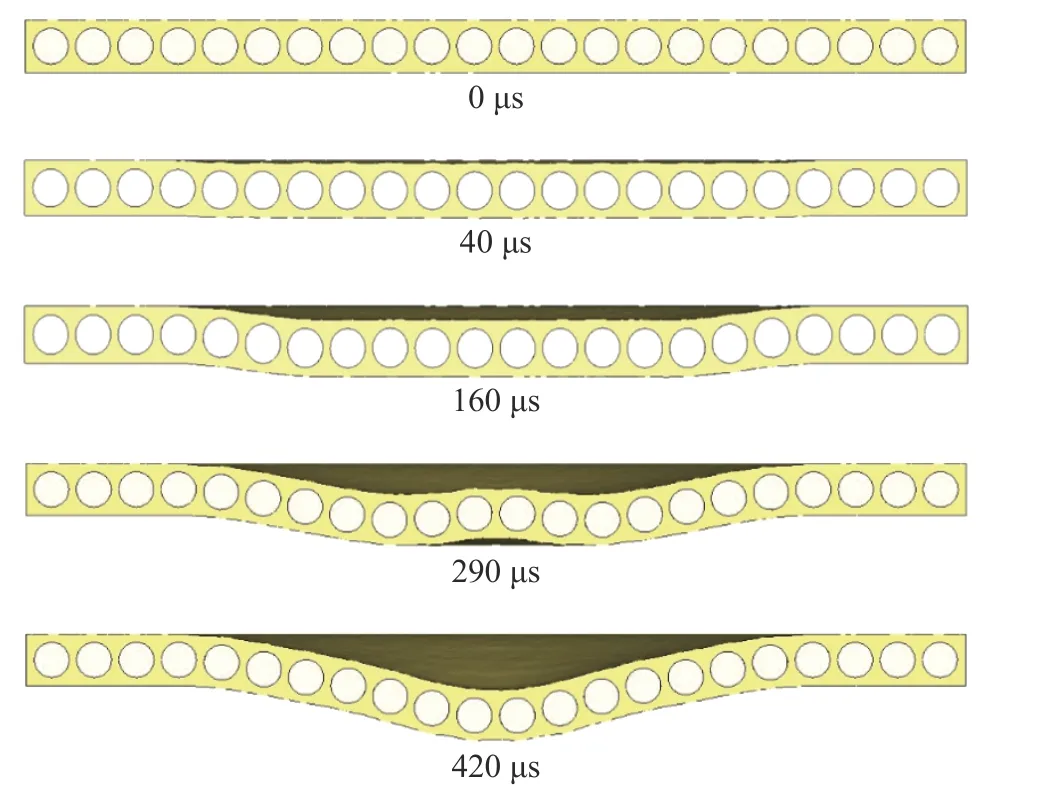
图10 变形历程Fig.10 Deformation history diagram

爆炸冲击波在接触复合材料板表面后的瞬间，整个板产生了很大的加速度，最大值达到3.63 ×105m/s2，随后复合材料板加速度峰值急剧下降，结合图11 中复合材料聚氨酯和陶瓷球部分的加速度曲线可以看出，聚氨酯与陶瓷球部分的加速度方向相反，当聚氨酯发生弹性变形时，陶瓷球会有一个相反的作用力使得聚氨酯的加速度减小，说明陶瓷球的存在有效减小了整体的加速度，起到了对复合材料板总体的支撑与缓冲作用，使得震荡幅值下降，保证了总体的稳定性。纯聚氨酯与复合材料板的整体加速度对比也验证了此结论。

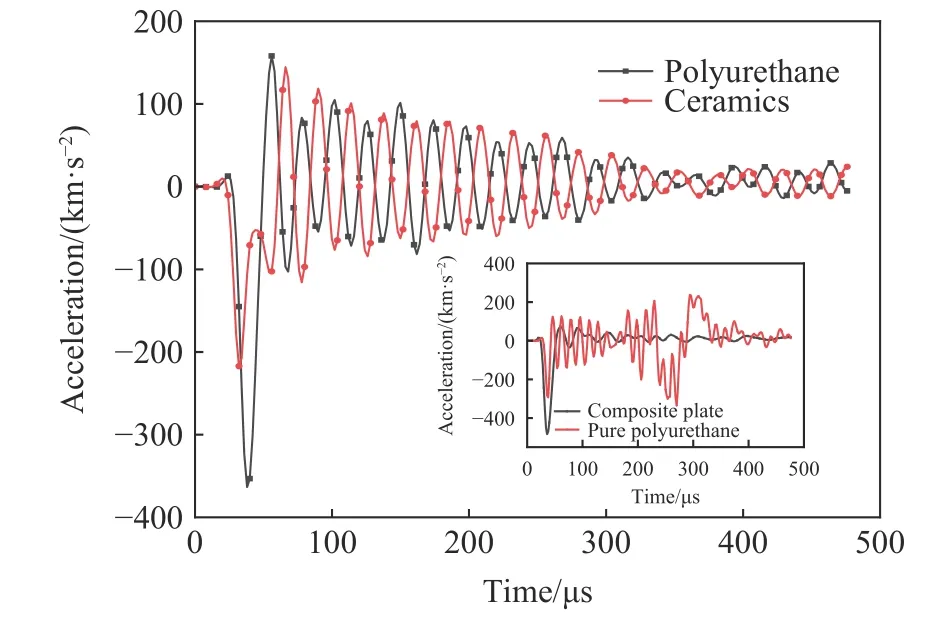
图11 不同材料板的加速度对比曲线Fig.11 Acceleration comparison curve

通过选取图9 中部分点的速度曲线可以看出，在50 µs 后，板上各点速度开始出现很大差异，如图12所示，板边缘的速度逐渐下降，越靠近中心，速度变化越大。复合材料板的最大速度为45.17 m/s，出现在约335 µs。中心点的垂直速度在225～275 µs 的时间内小于距背板中心点10 和20 mm 处的速度，与上述出现中心位移小于四周的情况一致。

图12 复合材料底部距中心不同距离点的速度曲线Fig.12 Velocity curves of different distance points from the bottom of composite to the center

3.3 爆炸当量对复合材料板变形与吸能的影响

为探究复合材料板受到当量爆炸载荷下的动态响应，添加TNT 当量W为2、4 和5 g 进行计算。结果如图13 所示，结合爆炸当量为3 g 的位移/速度曲线可以看出：当爆炸当量增大时，复合材料板背波面中心点达到最大挠度的时间相较提前，这主要是由于随着爆炸当量的增大，冲击波在空气中的传播速度也会随之升高，导致复合材料板与冲击波接触的时间提前，通过复合材料板迎波面的压力变化数据可以得到当爆炸当量为2、3、4 和5 g 时，接触时间分别为31.99、29.99、27.99 和25.98 µs。而复合材料板到达最大挠度的时间分别为483、476、473 和457 µs。可以看出，冲击波与板接触时间的提前是复合材料板到达最大挠度时间提前的主要原因。

图13 不同爆炸当量下背波面位移/速度曲线Fig.13 Displacement/velocity curves at the back wavefront for different explosion equivalents

爆炸当量为2 、3 和4 g 时复合材料背板最大挠度分别为5.82 、7.23 和8.50 mm，挠度增量分别为1.41 和1.27 mm。而当爆炸当量为5 g时，复合材料背板最大挠度为9.83 mm，挠度增量为1.33 mm。在小爆炸当量的前提下，当量每提升1 g，所引起的复合材料板最大挠度增长在一个相对稳定的值，为预测陶瓷球增强聚氨酯复合材料板的力学性能提供了一定的参考。

复合板在不同当量下底部距中心点的速度如图13 所示。不同爆炸当量下复合材料板中心点的速度在50 µs 以前并无太大差异，在50 µs以后出现较大差异。底部中心点的速度变化最大，爆炸当量为2 g 时，最大速度为33.16 m/s；爆炸当量为4 g 时，最大速度为56.75 m/s；爆炸当量为5 g 时，最大速度为65.75 m/s。

聚氨酯弹性体作为良好的吸能材料，其在爆炸载荷下的吸能远远高于陶瓷部分，由图14可以看出，在爆炸当量为2 g 时，复合材料中聚氨酯的吸能约为陶瓷的2 倍，此数值在爆炸当量为3、4 和5 g 时分别为2.9 倍、3.2 倍和4.0 倍。爆炸当量为5 g 时，在复合材料中占整体质量47%的聚氨酯的吸能占到了总吸能的80%。并且随着爆炸当量的增大，聚氨酯的吸能效率变得更高，证明陶瓷颗粒增强聚氨酯复合材料既可以拥有纯聚氨酯的吸能效果，又具有纯聚氨酯不具备的稳定性。

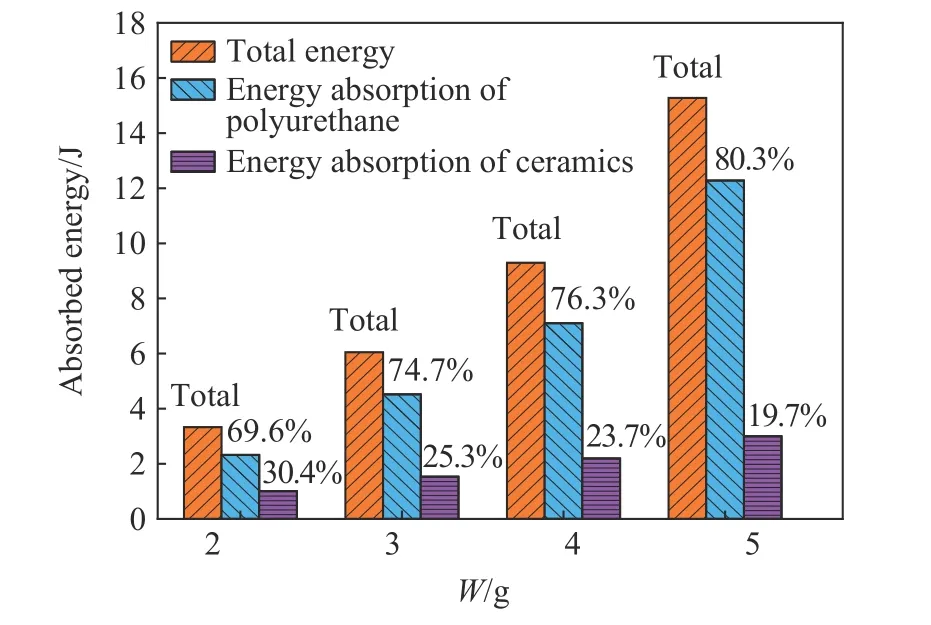
图14 不同爆炸当量时，不同材料吸能对比Fig.14 Comparison of energy absorption of different materials at different explosion equivalents

4 陶瓷球尺寸对复合材料板变形与吸能的影响

为探究陶瓷球尺寸对聚氨酯基复合材料性能的影响，设定复合板的面密度ρs为：

式中：Vs为复合板体积，nc为陶瓷球数量，rc为陶瓷球半径，S为复合板表面面积，ρc和ρj分别为陶瓷和聚氨酯的密度。在保持复合板整体尺寸不变的情况下，填入不同半径的陶瓷球，通过改变陶瓷球数量来保持面密度基本相同。表4 所示为陶瓷球直径变化时，陶瓷球数量nc、面密度ρs、陶瓷球间距d以及质量占比m对应关系。

表4 陶瓷球尺寸参数Table 4 Dimension parameters of ceramic ball

将陶瓷球直径分别为3.0 mm（共1613 个）和6.0 mm（共203 个），交叉排列放入长宽均为120 mm、厚度为6.5 mm 的聚氨酯中，排列方式如图15 所示。

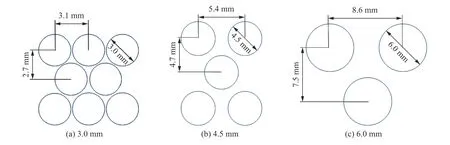
图15 不同直径陶瓷球模型Fig.15 Ceramic ball models with different diameters

爆炸当量为3 g 得到复合材料板背波面中心点挠度如图16 所示，可以看出，在131 µs 前，不同直径陶瓷球复合材料板挠度变化并无差别。直径3.0 mm 的陶瓷球的复合材料在369 µs 时达到最大挠度为5.9 mm，而直径4.5 和6.0 mm 的陶瓷球的复合材料分别在475 和514 µs 时分别达到最大挠度7.2 和8.5 mm。这说明在相同载荷下，陶瓷球直径越小，复合材料板抵抗变形的能力越强。

图16 爆炸当量为3 g 时不同直径陶瓷球的位移曲线Fig.16 Displacement curves for ceramic balls of different diameters with explosion equivalent 3 g

图17 给出了爆炸当量为3、4 和5 g 时复合材料板背波面的最大挠度曲线，可以看出随着爆炸当量的提升不同直径陶瓷球复合材料板的最大挠度近似呈线性增长。图中曲线的斜率k随陶瓷球直径增大而变大，复合材料板对冲击载荷的敏感度也变大，由此得到相同面密度下直径越小的陶瓷球复合材料板在受到大冲击载荷时将会有更好的抵抗能力。

图17 不同直径陶瓷球背波面中心点的挠度曲线Fig.17 Deflection curves of center points of back wave surfaces

图18 所示为直径为3.0、4.5 和6.0 mm 时陶瓷球复合材料板的能量吸收曲线。随着陶瓷球直径变大，吸收能量在陶瓷球直径为6 mm 时增大较多。分析原因，虽然陶瓷球直径不同，但由表3 得出质量占比并无太大差距，吸收能量应保持在一定范围内，但由于6.0 mm 直径的陶瓷球与复合材料板间距过大，导致整体变形变大，增加了复合材料板内能吸收，进而增加了总体吸能。

图18 爆炸当量为3 g 时不同直径陶瓷球的吸能曲线Fig.18 Energy absorption curves for ceramic balls of different diameters with explosion equivalent 3 g

图19 所示分别为3.0、4.5 和6.0 mm 陶瓷球复合材料板的加速度，最大加速度分别为5.14 ×105、4.83×105和3.35×105m/s2，可以看出，随着陶瓷球增大，加速度最大值随之减小，且加速度的波动范围也随之变小，复合材料板更加稳定。

图19 爆炸当量为3 g 时不同直径陶瓷球的加速度曲线Fig.19 Acceleration curves for ceramic balls of different diameters with explosion equivalent 3 g

5 结 论

本文中基于LS-DYNA 的ALE 流固耦合方法，对爆炸载荷下不同尺寸毫米级陶瓷球增强聚氨酯复合材料板的动态响应过程进行模拟，分析其动态响应特性，得到结论如下。

(1)在爆炸冲击波的作用下，复合材料板背波面在225～275 µs 内中心点挠度小于周围点的，速度也呈现出中心点比周围点低的现象。此外，由于陶瓷球与聚氨酯的加速度始终保持相反方向，添加了陶瓷球的聚氨酯复合材料整体加速度波动范围较纯聚氨酯低约1×105m/s2。

(2)随着爆炸当量每提高1 g，复合材料板到达最大挠度的时间提前约5 µs，复合材料板的挠度增长都处于一个相对稳定的值，约为1 mm，为预测陶瓷球增强复合材料板的力学性能提供了一定的参考，且聚氨酯的吸能占总吸能的比重由爆炸当量为2 g 时的69.6%增长为5 g 时的80.3%。

(3)在复合材料板整体尺寸与面密度不变的情况下，陶瓷球直径为3.0、4.5 和6.0 mm 时，最大变形挠度分别为5.9、7.2 和8.5 mm，复合材料板抵抗变形的能力随着陶瓷球直径增大而增强，总体加速度波动范围也随之变大，复合材料板对冲击载荷的变化敏感度由1.05 变为了1.60。对于陶瓷球的尺寸与间距变化带来的微结构性能差异，还需要做进一步的研究。