铆接油箱的水锤毁伤效应*

张景飞，贾豪博，任柯融，卿 华，郭 攀，杜晓伟，陈 荣，卢芳云

（1.郑州大学力学与安全工程学院，河南 郑州 450000；2.国防科技大学理学院，湖南 长沙 410008；3.空军工程大学航空机务士官学校，河南 信阳 464000）

燃油系统是飞机易损部件中暴露面积最大的系统，其安全性对于飞机作战生存力至关重要。当射弹以极高的速度冲击充满液体的容器时，射弹携带的动能将转化为液体的冲击波能量，并最终以液体压力波的形式传递到容器壁面，从而对容器结构造成巨大破坏，这种流-固耦合现象称为水锤效应[1]。据统计，在美军开展的“沙漠风暴”行动中，有75%的飞机战斗损伤事件都与油箱受损有关，且在这些飞机战斗受损事件中水锤效应导致的战损比例最大[2]。

为了研究水锤效应对油箱的毁伤机制，自20 世纪70 年代开始就有学者开展了大量的实验。Ball[3]首先使用不同能量等级的射弹对充液箱体进行了水锤效应的实验研究，测量了射弹侵彻油箱过程中的液体压力和入射板应变，发现影响射弹能量衰减的主要因素是射弹的质量和入射角度。Disimile 等[4]使用不同材料的射弹冲击模拟油箱，记录了油箱中不同位置的压力数据，分析了射弹冲击油箱时流体压力的空间分布规律。Varas 等[5]使用质量为8 g 的钢球以不同的速度、不同的充液比进行了射弹撞击充水铝管的实验，研究了射弹速度和油箱充液比对水锤效应的影响。Ren 等[6]采用不同形状的射弹以不同的速度撞击油箱，建立了射弹动能、形状与容器壁板变形的关系。李营等[7]设计了水间隔靶板在球形弹体撞击下动态响应的实验装置，对比了不同靶板在弹体侵彻作用下的变形特点。陈安然等[8]等通过开展高速破片侵彻充液容器的实验，得到了水锤效应引起的液体喷溅特性及其影响因素。近些年，随着计算机技术的快速发展，有限元方法成为了一种实用高效的数值分析方法，并逐渐应用于各个科学领域。李亚智等[9]通过MSC.DYTRAN 软件对空箱和充液油箱在高速弹丸冲击下的动态响应进行了数值模拟，得到了2 种箱体壁板的应力、应变时间历程。Varas 等[10]使用了ALE 算法模拟了钢球弹丸冲击充水铝管所产生的水锤效应，并与实验结果进行对比，验证了ALE 算法可以较为真实地模拟水锤效应的各个阶段。Mansoori 等[11]模拟了射弹冲击充水容器和不充水容器的整个过程，分析了容器壁面的失效形式。蓝肖颖等[12]建立了双射弹冲击充水油箱的有限元模型，研究了液压水锤的叠加效应。韩璐等[13-14]对飞机油箱水锤效应的影响因素和影响程度进行了综合分析。

在上述研究中，所关注的研究对象主要集中于通过螺栓固定的模拟等效油箱，而对具有飞机结构特征油箱关注较少。真实的飞机油箱结构大多是通过铆接进行连接固定的。陈钢[15]研究发现，在常规金属结构中，构件之间的连接接头是最容易被破坏的部位。飞机结构中的铆钉本来设计为以剪切力的形式进行载荷传递；然而当机翼油箱壁板（或机翼蒙皮）被液压水锤垂直作用时，会发生弯曲变形，从而导致连接这些壁板的铆钉将处于纵向拉应力和横向剪切应力同时作用的复杂应力状态下。如果铆钉无法承受这种复杂应力加载，将发生断裂失效，最终导致油箱壁板（或机翼蒙皮）脱落[16]。为了对液压水锤载荷下的油箱接头强度进行定量评估，莱特-帕特森空军基地开发出了水锤模拟器[17]，该设备可以对飞机结构接头进行可控的液压水锤加载，从而获取了接头的动态破坏极限，验证了以承受剪力为主的铆接接头在水锤载荷的正向加载下并不具备理想的动态强度，但是他们并没有考虑水锤对铆接油箱的整体毁伤效应。

为了探究铆接油箱在水锤作用下的动态响应机制，本文开展对铆接油箱的弹道射击实验，结合数字图像相关测试技术，测量铆接油箱在射弹冲击作用下的箱体变形、破孔直径等数据；并进行流固耦合的有限元数值模拟，分析射弹入射速度与射弹动能损失、箱体变形、流体动压、铆钉失效之间的规律；结合实验和模拟结果，探索铆接油箱在速度为780～1600 m/s 的钨合金射弹冲击下的动态力学响应行为及水锤对铆接油箱的毁伤机理，建立射弹入射参量-水锤参量-铆接油箱毁伤参量的映射关系。

1 实验设计

采用弹道射击实验对铆接油箱进行水锤加载，实验现场整体布置如图1 所示。实验装置主要包括弹道枪、测速靶、铆接油箱以及高速摄像机。

图1 实验场景布置Fig.1 Experimental layout

实验中使用的射弹质量为69.7 g，长度为51.6 mm，直径为10.8 mm，形状为尖头形，材质为钨合金。射弹由一门12.7 mm 口径的弹道枪发射，设计着靶速度为780 m/s，射击瞄准点为油箱前壁板的几何中心位置。采用断靶法测试射弹的入射速度，将2 张测速靶布置于油箱正前方约10 m 处。

铆接油箱为长方体结构，尺寸为440 mm×190 mm×416 mm，由6 块2024 铝合金板铆接而成，内部填充95%容量（约23.4 L）的航空煤油。前后壁板厚度为2 mm，油箱其余壁板厚度为3 mm。油箱上的铆钉分为2 种，一种是用来连接油箱上下壁板和侧壁板的304L 不锈钢铆钉，另一种是连接前后壁板和其余壁板的5052 铝合金铆钉，其直径均为4 mm。

实验中，使用1 台高速摄像机记录整个撞击过程，拍摄频率为300 000 Hz，位于油箱前方45°方向10 m 处。同时，为了记录油箱后壁板的变形情况，将2 台高速摄像机设置在油箱侧后方3 m 处，拍摄频率为50 000 Hz，对拍摄的结果进行数字图像相关（digital image correlation, DIC）技术处理[18]以获取后壁板的应变场历史。

2 有限元数值模拟

为了更好地模拟射弹高速冲击下油箱箱体及航空煤油的动力学响应过程，采用ALE 流-固耦合算法进行仿真计算[5]。图2 为所建立的与实验相同尺寸的有限元模型，模型包括油箱箱体、射弹、煤油、空气和铆钉5 部分，其中流体域包括煤油和空气，使用多物质Euler 单元描述；固体域包括油箱箱体、射弹和铆钉，使用Lagrange 单元描述，模型中的所有单元均采用六面体单元划分。为了提高计算精度，并控制计算成本，本文采用1/2 平面对称模型进行计算，并将射弹运动路径周围的单元进行加密划分，未加密区域单元尺寸约为4 mm，加密区域单元尺寸约为1 mm，整个模型共包含1 602 566 个单元。空气域四周设为无反射边界条件，油箱箱体之间以及油箱箱体和铆钉之间使用关键字*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE 定义为自动面-面接触，射弹和油箱前后壁板之间使用关键字*CONTACT_ERODING_SURFACE_TO_SURFACE 定义为侵蚀面-面接触。在建立有限元模型时，将流体域的空气和煤油单元之间进行共节点处理，利用关键字*CONSTRAINED_LAGRANGE_IN_SOLID实现Lagrange 单元和Euler 单元之间的相互作用，进而实现流-固耦合计算。

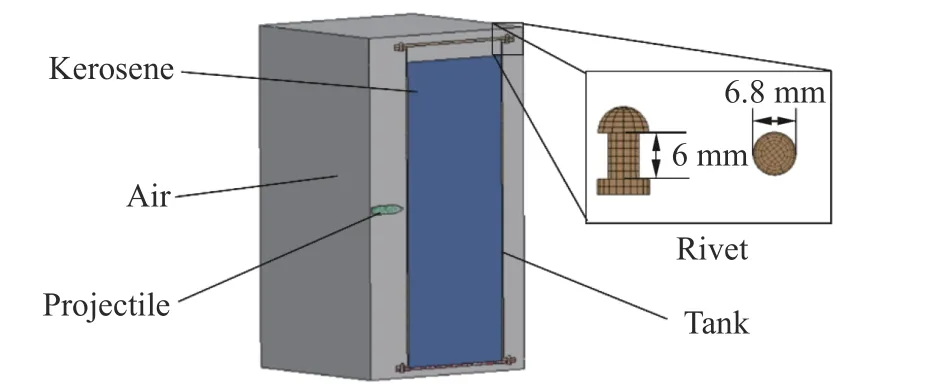
图2 有限元模型Fig.2 Finite element model

在材料模型方面，射弹和箱体分别为钨合金和2024 铝合金，使用 Johnson-Cook 本构模型、Johnson-Cook 失效模型和Grüneisen 状态方程描述，具体取值详见文献[19-20]。铆钉材料为304L 不锈钢和5052 铝合金，使用塑性随动（plastic kinematic, PK）本构模型和等效塑形应变（equivalent plastic strain,EQPS）失效准则描述，具体取值详见文献[21-22]。在EQPS 失效准则中，当单元的EQPS 值达到临界值时，就会被删除，不参与下一步的计算。煤油和空气分别采用Grüneisen 状态方程和先行多项式状态方程描述，具体取值详见文献[23]。

Johnson-Cook 本构模型[20]广泛的应用于描述材料的大变形行为，其屈服应力表达式为：

式中：A为材料初始屈服应力；B为材料应变硬化模量；n为硬化指数；Cj为材料应变率参数；m为材料热软化参数；为等效塑形应变，为应变率=1 s−1的塑性比，为等效塑性应变率；相对温度Th=(T−Tr)/(Tm−Tr)，Tr为室温，Tm为熔点。

在Johnson-Cook 失效模型中，材料的失效应变εf表达式[20]为：

式中：σe和σh为等效应力和静水压力；当损伤参数时材料发生断裂，Σ 代表对断裂前的变形过程求和；为等效塑性应变增量；D1～D5为常数。

Grüneisen 状态方程[24]用于定义物质在压缩和膨胀状态下的压力变化，其表达式为：

式中：p1、p2分别为压缩材料和膨胀材料的压力；c0为声速体积；S1、S2、S3为材料参数；γ0为 Grüneisen 系数，a为 γ0的一阶体积修正系数；u=ρ/ρ0−1，ρ 为某一静水压力下材料的瞬时密度，ρ0为材料的初始密度，e为单位体积的初始内能。

在PK 本构模型[21]中，塑性流动应力与塑形应变、应变率具有如下关系：

式中：σ0为初始屈服应力，为应变率，为有效塑形应变，β 为硬化参数，Ep为塑性硬化模量，Cpk、P为应变率参数。

3 结果与讨论

3.1 实验结果与仿真模型验证

图3 为实验测试得到的不同时刻油箱后壁板z轴方向的位移云图，同时给出了有限元计算结果进行对比。起始时刻为射弹击中油箱前的时刻。从图中可以看出随着时间的推移，油箱后壁板的变形将逐渐增大。

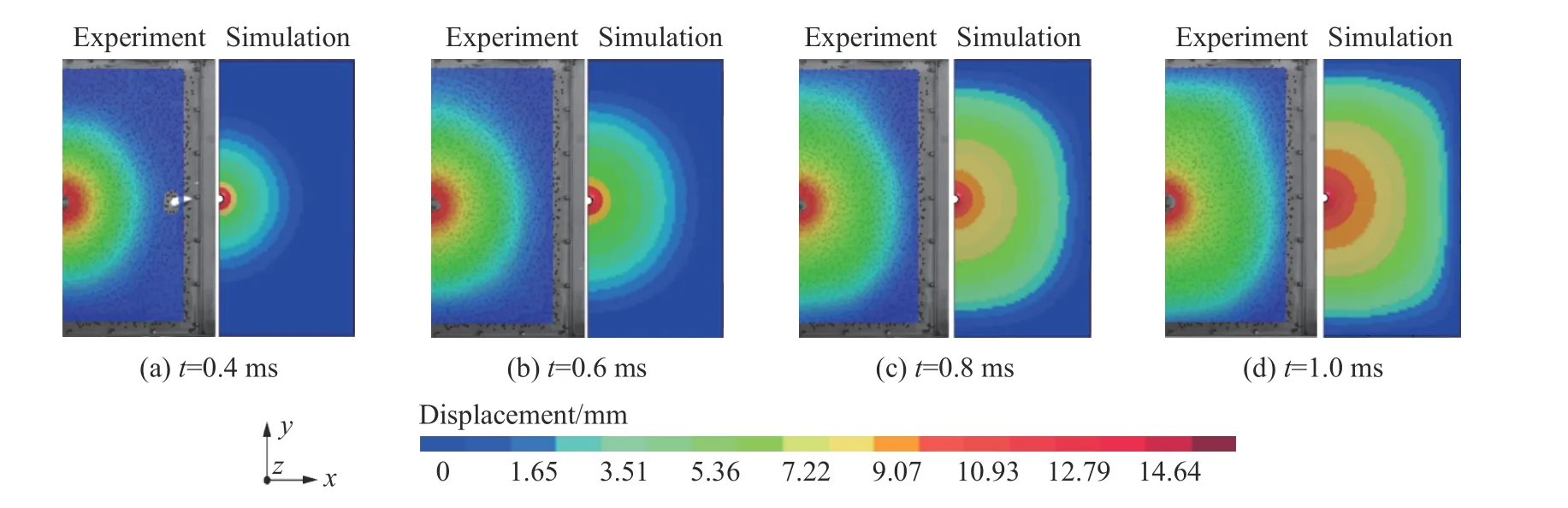
图3 不同时刻实验与模拟中的油箱后壁板变形云图对比Fig.3 Comparison of deformation contours of the back wall of the fuel tank in experiment and simulation at different time

图4 给出了实验和模拟得到的后壁板变形结果对比。其中，实验和模拟结果的相关系数使用Pearson 公式[25]计算，表达式如下：

图4 不同时刻油箱后壁板z 轴变形Fig.4 z-axis deformation of the back wall of the fuel tank at different times

式中：cov(X,Y)为两组数据X和Y的协方差；σX、σY分别为X和Y的标准差；E(X)、E(X)、E(XY)分别为X、Y、XY的期望值。|R|越接近1，表示两组数据的相关性越强。

如图5 所示，测量实验和仿真结果中后壁板的破孔尺寸分别为15 和14 mm，相对误差为6.67%。图6给出油箱后壁板弹孔上方20 mm 处壁板单元的速度时程曲线，从图可以看出，该点在射弹入射油箱后0.28 ms 左右达到了速度峰值，其中实验和仿真所得速度峰值分别为51.81 和54.84 m/s，误差为5.81%。因此，本文所建的有限元模型计算精度较好，能够较好地描述实验结果。

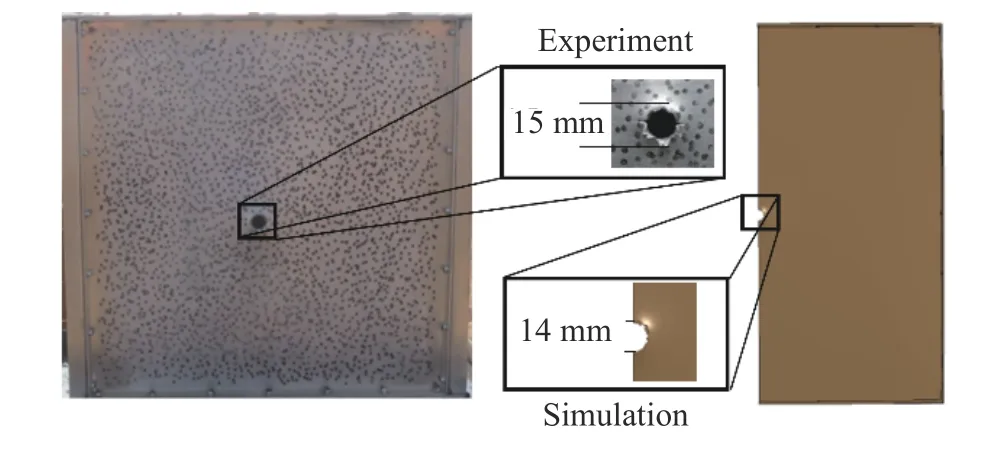
图5 后壁板破孔实验结果和模拟结果的对比Fig.5 Comparison of the experiment result and the simulation result of the broken hole in the back wall

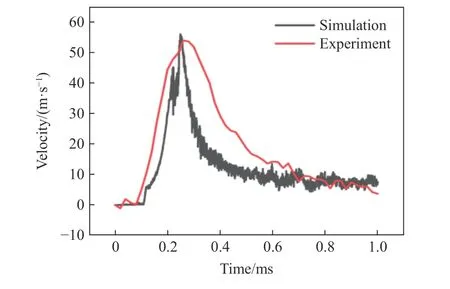
图6 后壁板弹孔上方20 mm 的速度Fig.6 Velocity of units at 20 mm above the projectile hole in the back wall

3.2 铆接油箱在水锤作用下的毁伤规律

3.2.1 射弹运动过程及动能衰减分析

为了进一步探究铆接油箱在具有不同初始动能射弹作用下的毁伤规律，开展了射弹以780、1000、1200、1400、1600 m/s 等5 个速度工况垂直入射油箱的有限元计算。当射弹击中油箱时会在油箱箱体和煤油的作用下做减速运动，并将一部分动能转化为自身的变形能、煤油的动能和内能以及油箱箱体的动能和变形能。仿真计算所得的射弹加速度随时间变化曲线如图7 所示，从图中可以看出射弹在侵彻油箱的过程中主要经历3 个阶段：

图7 射弹加速度时程曲线Fig.7 Projectile acceleration history curves

(1) 射弹击中油箱前壁板时加速度急剧增大，速度快速下降；根据动量方程可知射弹撞击油箱壁时所产生的冲击力与射弹的速度成正比，因此当射弹入射速度为1600 m/s 时，加速度最大，达到了106m/s2；

(2) 射弹在煤油中运动阶段，加速度保持稳定，速度稳步下降；射弹在液体中的运动阻力表达式[23]如下

式中：f为射弹在液体中运动所受阻力；cd为阻力系数，与液体雷诺数有关，在数值计算中通常假设液体不可压缩，因此cd为常数，取值0.275[14]；ρl为液体密度；v为射弹速度；S为射弹横截面积。由式(7)可知，同一种形状和材质的射弹在煤油中运动时所受阻力与射弹速度的平方成正比，因此射弹入射速度为1600 m/s 时在煤油中运动的加速度相较1400 m/s 入射时提高了33.8%；

(3) 在射弹穿出油箱后壁板前，流体内的冲击波提前到达后壁板，并在后壁板处产生预应力。

图8 给出了油箱前、后壁板对射弹施加的侵彻阻力以及射弹到达后壁板前冲击波对后壁板中心与弹道线交汇处单元施加的预应力。从图中可以看出油箱前壁板对射弹施加的侵彻阻力明显大于后壁板，当射弹入射速度从780 m/s 提升到1600 m/s，油箱前壁板对射弹施加的侵彻阻力从16.75 kN 增加到56.8 kN, 而油箱后壁板对射弹造成的侵彻阻力则维持在20 kN 左右，同时煤油内的冲击波对油箱后壁板造成的预应力也从441 MPa 提高到537 MPa。可见，射弹的速度越大，在煤油中内形成的冲击波越强，对油箱后壁板产生的预拉应力也就越大；而预拉应力越大使得后壁板更容易被侵彻[26]，因此导致后壁板的对不同速度射弹的侵彻阻力都恒为一个定值。

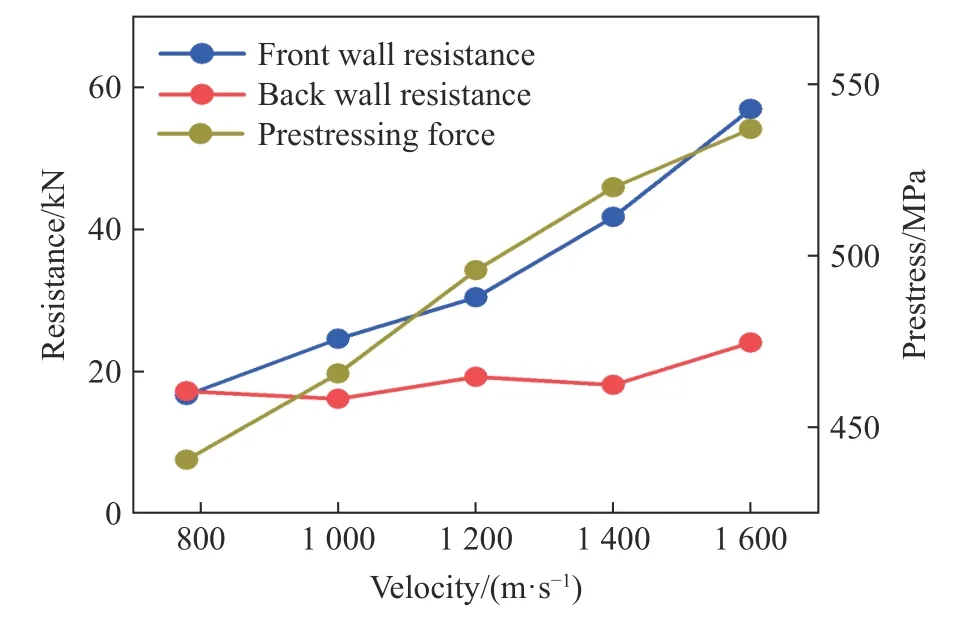
图8 油箱前后壁板对射弹的阻力及冲击波对后壁板单元的预应力Fig.8 Projectile resistance from the front and back walls of the tank and prestress of the back wall elements by the shock wave

图9 给出射弹在不同入射速度下的动能损失变化关系。从图7、图9 中可以看出，当射弹入射速度为1600、1400、1200、1000 m/s 时，在煤油内运动的加速度相较与780 m/s 分别提高了405.9%、259.2%、160.9%、66.3%；出射时间分别提前了0.125、0.109、0.084、0.049 ms；动能损失增加了1341、901、504、210 J。因此，射弹入射速度越高，在煤油中运动所受的阻力越大，贯穿油箱所用的时间越短，动能损失越多。

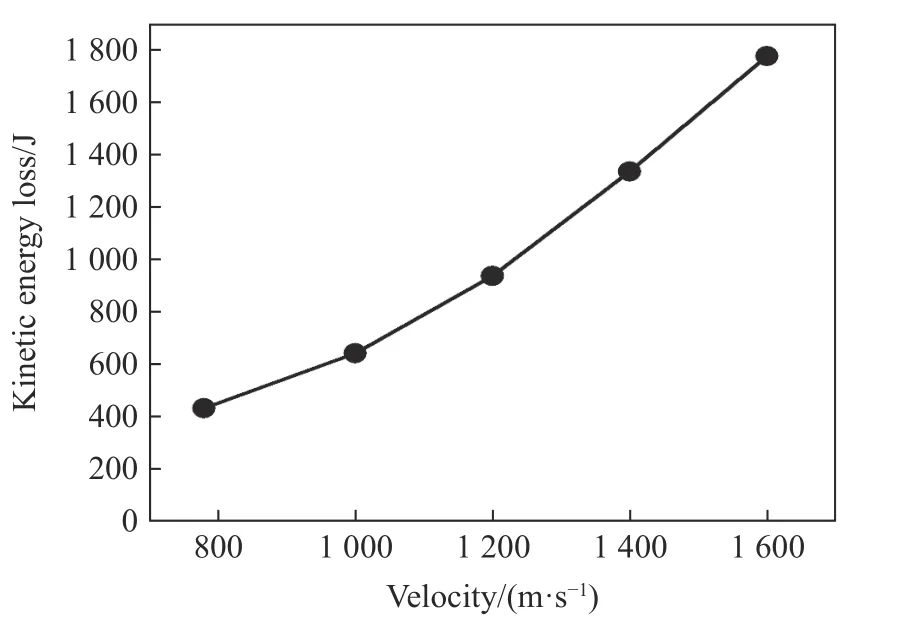
图9 射弹入射速度对动能损失的影响Fig.9 Influence of projectile incident velocity on kinetic energy loss

3.2.2 油箱液体压力分析

图10 是在射弹在780～1600 m/s 的速度下煤油内的压力云图，可以看出当射弹撞击煤油时，会在煤油内产生初始冲击波。其中，射弹头部周围形成的冲击波强度最大，并且随着冲击波传递距离的增加，强度不断衰减。

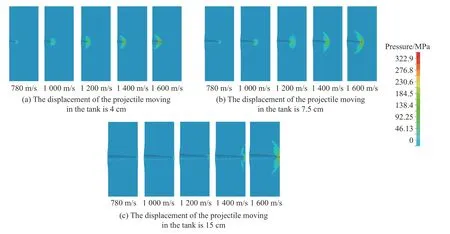
图10 不同射弹入射速度下煤油的压力分布演化Fig.10 Pressure contours of kerosene at different projectile impact velocities

图11 给出了射弹入射速度、初始冲击波强度与持续时间的变化关系，可以看出射弹入射速度越大，在煤油中形成的初始冲击波强度也越大，同时随着射弹入射速度的增加，穿透油箱所用的时间更短，因此初始冲击波持续的时间也越短。

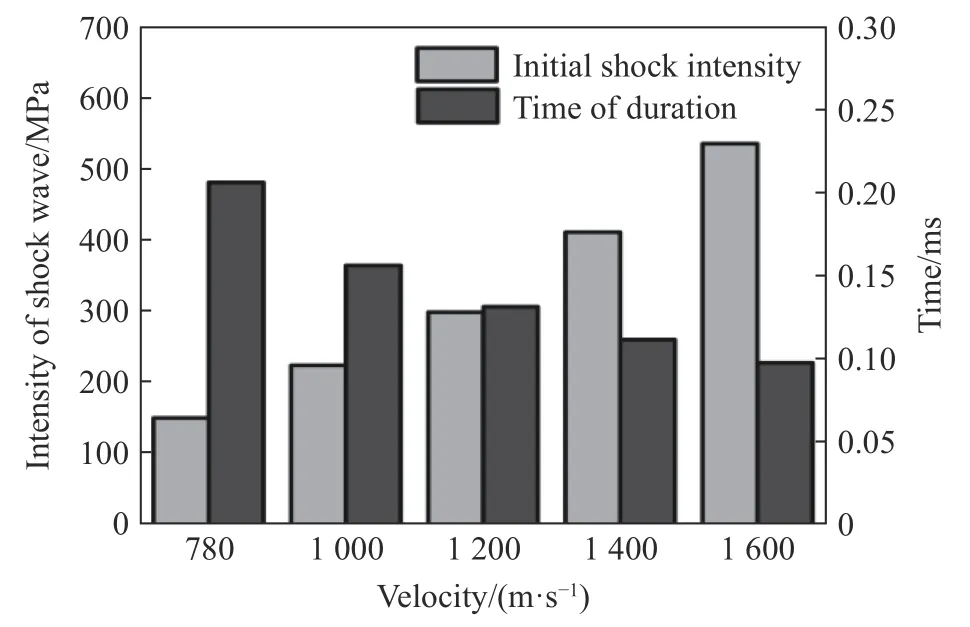
图11 射弹入射速度对初始冲击波压力和持续时间的影响Fig.11 Infuence of impact velocity of projectile on pressure of initial shock wave and its duration

为对比不同射弹入射速度下油箱侧壁面所受载荷大小，选取油箱右壁板中心处液体单元观察其压力变化。图12 为射弹以不同速度撞击油箱时油箱右壁板中心处煤油压力变化曲线。由于射弹撞击油箱后产生的冲击波波速与射弹穿透入射壁板所携带的能量呈正比例关系[27]，因此射弹入射速度越快，煤油压力峰值出现的时间越早，且峰值压力越大。如图13 所示，射弹入射速度为1600 m/s 时，峰值压力出现的时间相较780 m/s 时提前了0.0075 ms，而峰值压力大小提高了392.29%。同时可以发现侧向冲击波由于在传播过程中出现了衰减，导致其压力值迅速下降。例如，射弹速度为1600 m/s 时，煤油中形成的初始冲击波强度高达550 MPa，但是当冲击波传递到油箱右壁板时峰值压力衰减至仅7 MPa，因此油箱侧壁板的变形较小。

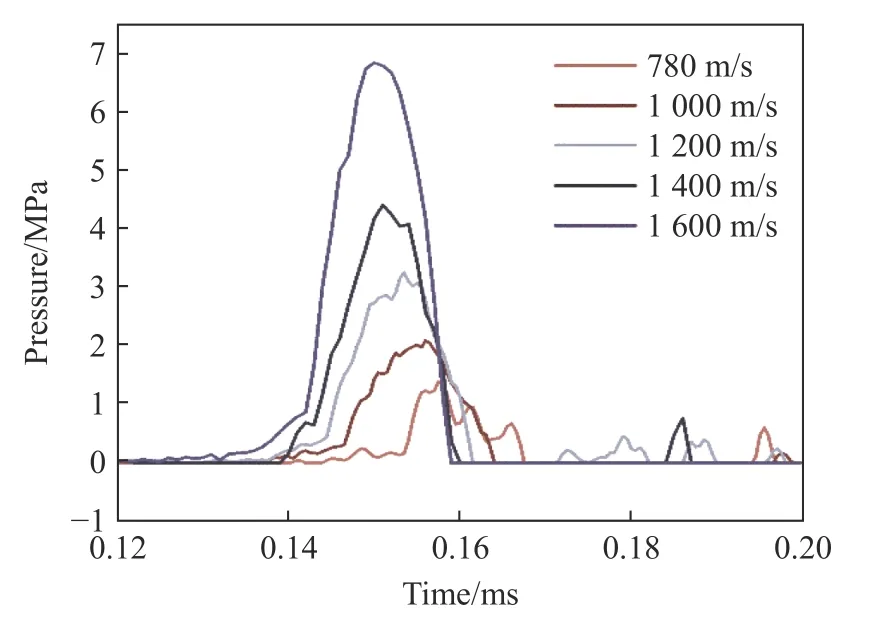
图12 壁面测点处的煤油压力时程曲线Fig.12 Time-history curves of kerosene pressure at measuring point on the side wall

图13 油箱前后壁板挠度变化Fig.13 Deflection evolutions of the front and back walls

3.2.3 油箱后壁板变形分析

当射弹高速侵彻油箱时，煤油吸收射弹动能后会转化为流体动压载荷，进而对油箱造成严重的变形与破坏。图13 给出了不同射弹着速下油箱前后壁板挠度变化的时程曲线图。对比图13(a)和图13(b)可以看出：油箱后壁板的变形程度明显大于油箱前壁板，如当射弹入射速度为1600 m/s 时，前壁板最大挠度（t=0.5 ms）为13.44 mm，后壁板最大挠度（t=0.5 ms）为27.64 mm，因此后壁板的毁伤程度甚于前壁板。

图14 和图15 分别为射弹在不同入射速度下油箱后壁板同一时刻的等效应力云图和破孔尺寸、裂纹尺寸、翘曲尺寸变化情况。从图中可以看出，后壁板的损伤主要有以下特点：(1) 当射弹入射速度小于1400 m/s 时，后壁板的损伤模式为冲塞失效、翘曲变形；当射弹入射速度达到1400 m/s 时，后壁板开始出现裂纹；并且随着射弹入射速度的增大，油箱后壁板裂纹逐渐向四周扩展；当射弹入射速度达到1600 m/s时，裂纹半径扩展到14.7 mm；(2) 后壁板的应力分布呈环状间隔分布，在破孔和裂纹处出现应力集中，并且射弹入射速度越大，后壁板的应力就越大；(3) 随着射弹入射速度的增大，后壁板的变形程度有着明显的增加，当射弹入射速度为1600、1400、1200、1000 m/s 时，后壁板最大翘曲尺寸是射弹入射速度为780 m/s 的1.13、1.45、1.81、2.3 倍。可见射弹入射速度的增加增强了水锤效应对油箱的破坏作用。

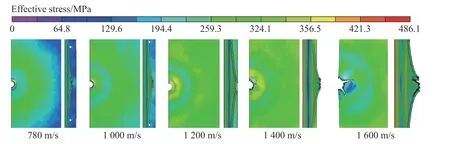
图14 后壁板等效应力云图Fig.14 Equivalent stress contours of the back wall

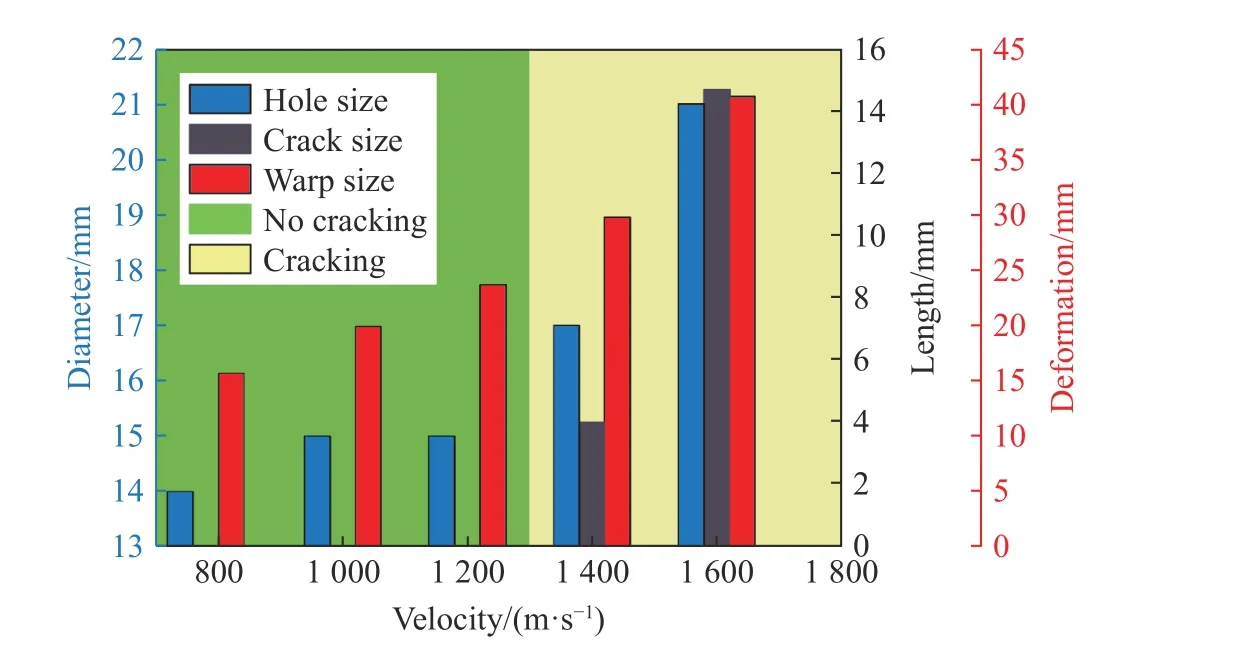
图15 不同射弹入射速度下后壁板的损伤模式演化Fig.15 Evolution of the damage patterns of the back wall at different projectile impact velocities

3.2.4 铆钉变形分析

对于铆接油箱来说，射弹在侵彻油箱的过程中，油箱箱体在射弹和液压水锤的作用下发生变形，同时还将带动着铆钉发生变形。因此射弹除了将自身的动能传递给煤油和油箱箱体外，还会将一部分能量转化为铆钉的变形能。当这一部分能量超过铆钉材料所能承受的极限时，铆钉就会发生断裂，从而造成油箱壁板脱离。本次实验及数值模拟中射弹的入射位置为油箱正中心，当射弹入射速度为1600 m/s时，油箱后壁板弹孔下方的铆钉最先发生断裂，之后相邻两侧的铆钉相继发生断裂 ，其余的铆钉发生了变形。图16、图17 分别给出油箱后壁板下侧中间位置铆钉发生最大变形时的等效应力云图和不同方向变形情况。可以看出：随着射弹入射速度的增大，铆钉的塑形变形也在增大，且铆钉的变形程度与射弹入射速度呈正比例关系；当射弹入射速度达到1600 m/s 时，铆钉中间部位单元达到了等效塑性应变的极限，因此发生断裂，此时单元的轴向拉伸应变为0.275，横向剪切应变为0.368。如图18 所示，当射弹速度到达1600 m/s 时，铆钉发生断裂失效，油箱后壁板有脱落风险。

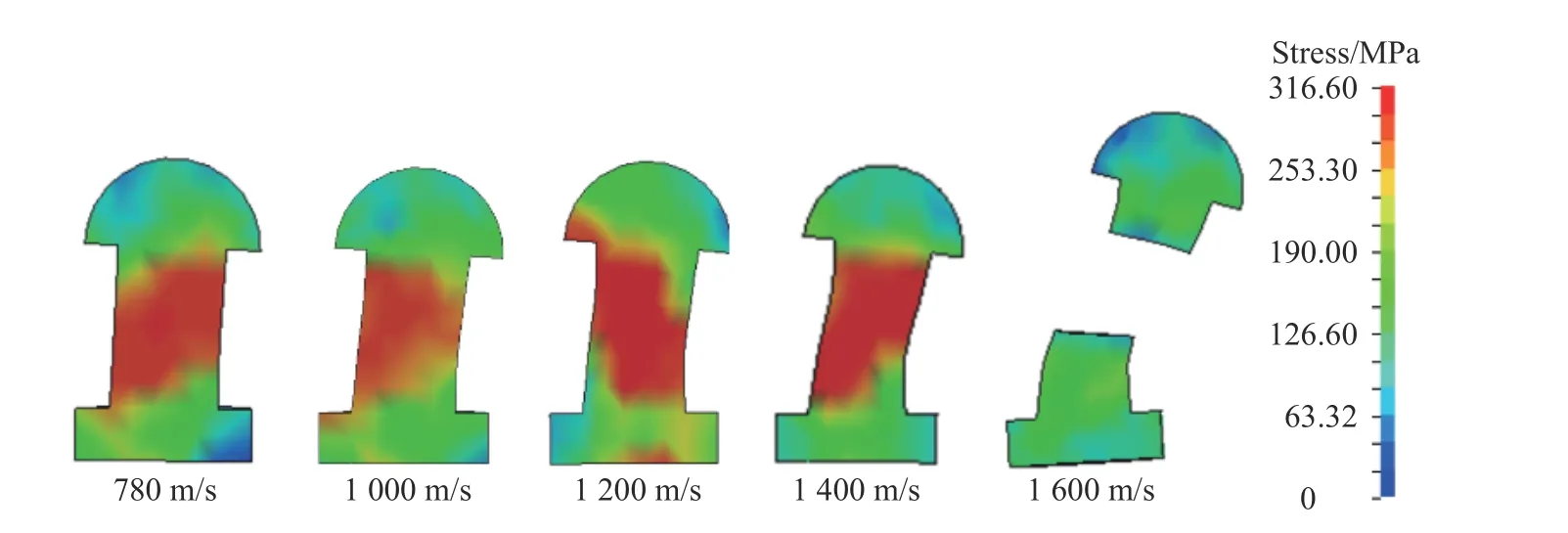
图16 铆钉发生最大变形时的等效应力云图Fig.16 Equivalent stress of the rivets contours at maximum deformation

图17 铆钉不同方向变形Fig.17 Rivet deflection at different directions

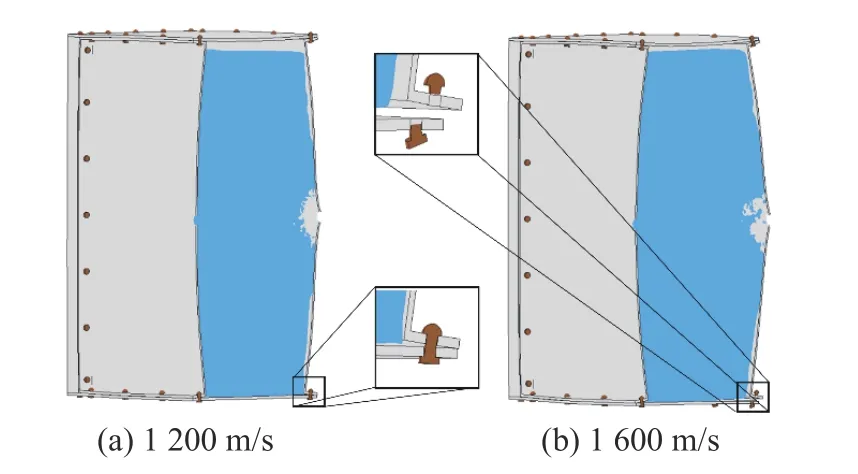
图18 不同射弹入射速度下铆钉变形对比Fig.18 Comparison of rivet deformation under different projectile impact velocities

图19 给出了射弹入射速度为1600 m/s 时，煤油、油箱前壁板、油箱后壁板以及铝合金铆钉的总能量（动能+变形能）时程曲线，图20 给出了射弹入射速度为1600 m/s 时，油箱后壁板和铝合金铆钉的动能、变形能（由于铆钉的动能太小，忽略不计）时程曲线。图中射弹入射时刻为0 时刻。可以发现煤油、油箱以及铆钉的能量变化存在以下特征：(1) 在射弹入射后至0.0995 ms 时，煤油的总能量急剧增加，同时前壁板能量也不断增加，说明在射弹入射初期，射弹的动能主要是转换为煤油的总能量以及前壁板的总能量；(2) 从0.0995 至0.1080 ms 时，煤油总能量陡峭下跌，同时后壁板总能量（主要是动能）迅速增加，此时水锤已经运动抵达后壁板，引起了后壁板的运动与变形；(3) 从0.1080 至0.6310 ms 时刻，射弹从后板穿出，由于失去了来自于射弹的能量输入，后壁板的总能量增长率明显放缓，并且在0.6310 ms 时刻后，后壁板的总能量开始减少，同时可以发现后壁板总能量明显高于前壁板总能量，即射弹动能绝大多数是被后壁板所吸收；(4) 在射弹于0.1080 ms 时从后壁板射出之后，后板的动能经过一小段时间的上升后就开始下降，变形能开始上升，同时铆钉的变形能也开始有了明显的上升，此时油箱后壁板在受到液压水锤的作用下发生塑形变形，并将自身的动能转移为变形能和铆钉的变形能；(5) 在0.715 ms 时，铆钉的变形能达到了34.5 J 并且开始小幅度的下降，此时铆钉发生了断裂。

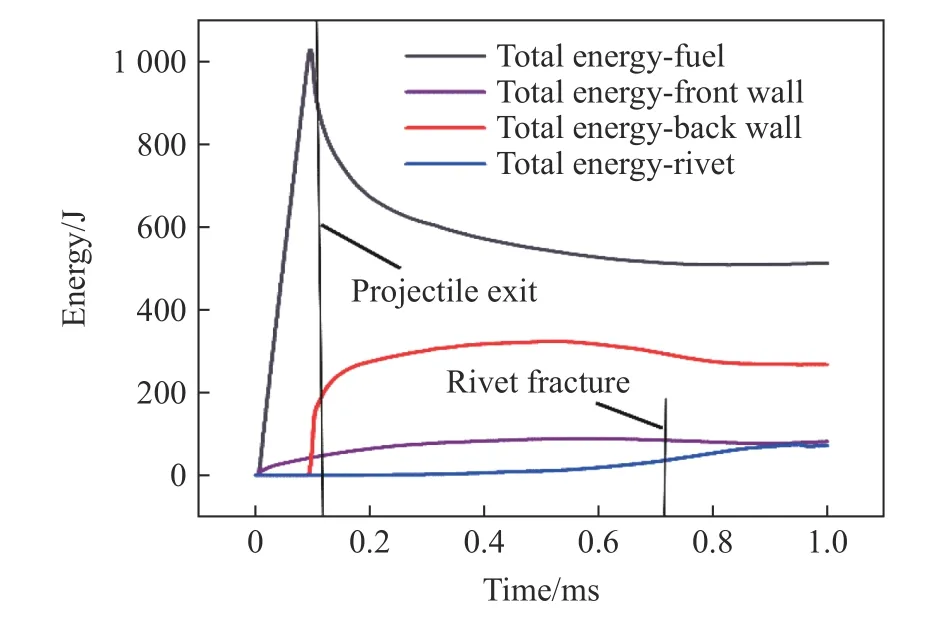
图19 油箱各构件总能量时程曲线Fig.19 Total energy curves for various parts of the tank

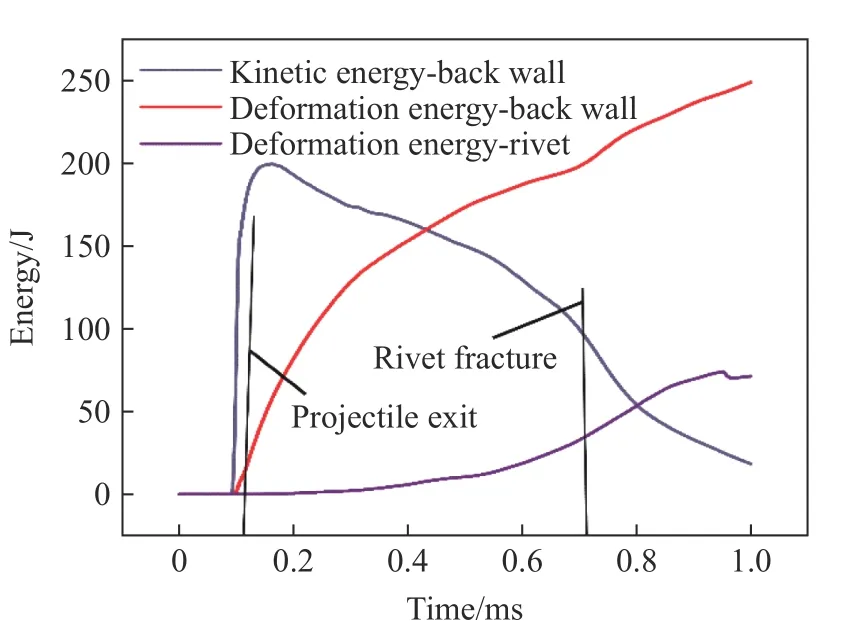
图20 壁板和铆钉能量变化时程曲线Fig.20 Energy curves of the back wall and the rivet

4 结 论

本文对铆接油箱进行了弹道射击实验与有限元数值仿真，并通过DIC 测试结果对比验证了数值模型的有效性。更进一步，通过有限元模拟研究了射弹在780～1600 m/s 速度冲击下铆接油箱的毁伤规律。主要结论如下：

(1) 射弹在侵彻油箱前壁板时速度急剧下降，之后在煤油内运动时的加速度趋于平缓；煤油内的冲击波相较于射弹将会提前到达油箱后壁板对其产生一个预应力，当射弹入射速度从780 m/s 提升到1600 m/s时，冲击波对油箱后壁板造成的预拉应力也从441 MPa 提高到537 MPa，导致虽然射弹入射速度逐渐提升，但是油箱后壁板对射弹的侵彻阻力一直维持在20 kN 左右；

(2) 射弹高速侵彻油箱会在煤油中产生初始冲击波，射弹入射速度从780 m/s 提升至1600 m/s，煤油内的初始冲击波强度从150 MPa 提升为550 MPa；初始冲击波以球面波的形式以入射点为中心向外扩展侧向冲击波衰减迅速，在射弹入射速度为1600 m/s 的情况下，煤油中形成的初始冲击波幅值高达550 MPa，到达右壁板时冲击波幅值仅为7 MPa，因此油箱侧壁板的变形较小；

(4) 在射弹侵彻与液压水锤的共同作用下，油箱后壁板会产生严重大变形，当射弹速度低于1400 m/s时，后壁板损伤模式以冲塞失效、翘曲变形为主；当射弹速度高于1400 m/s 时，后壁板损伤模式以花瓣型开裂、翘曲大变形为主；对于铆接油箱而言，由于油箱后壁板并不是固支边界，其变形将会带动边界变形，即铆钉变形；当射弹入射速度达到1600 m/s，铆钉发生断裂，油箱后壁板将出现脱落，有煤油大量泄漏的风险。