时变系统基于KDE的剩余寿命预测研究

张卫贞,石 慧,石冠男,吴 斌

(太原科技大学 电子信息工程学院,太原 030024)

近年来,随着机械系统不断向复杂化、大型化方向发展,对系统安全系数的要求也越来越高,系统的突然故障,可能导致其运行停止,甚至危及人身或财产安全[1]。因此,在工业大数据背景下,对系统健康状态进行有效监测、评估并准确地预测其剩余寿命具有非常重要的现实意义[2]。

现有的剩余寿命(RUL,Remaining Useful Life)预测方法主要有:物理模型、基于专家知识的模型和基于数据驱动的预测模型等[3]。对于复杂系统,物理模型的建立往往十分困难[4],专家知识也不够齐备[5],因此,数据驱动方法在实际中应用较多。Yan M等[6]利用支持向量机建立剩余寿命预测中的退化模型。Liu Q等[7]将部件的退化过程建模为离散的半马尔科夫过程。Si[8]对近年来基于数据驱动的预测模型进行了综述。但这些基于数据驱动的预测方法,在进行预测模型假设与参数估计时,往往与实际存在较大误差[9]。

另外,实际运行中机械系统的参数随时间不断演化。Bian等[10]将时变运行条件描述为均匀的马尔科夫链,并通过建立线性维纳过程分析其对退化过程的影响。Zheng Zhou等[11]将剩余寿命预测化为时变轨迹建模问题,并提出了一种动态控制网络来识别寿命观测序列中RUL轨迹的方法。Junqi Long等[12]提出了一种随机混合系统方法,但随着工况状态数的增加,预测精度会不断降低。人工神经网络在训练过程需要大量高质量观测数据,但实际中却无法或较难获得,以及人工智能技术的“黑匣子”特性,使得智能学习方法透明度低。

核密度估计(KDE,Kernel density estimation),对数据分布的形式不作任何假定,从数据本身出发研究数据分布的特征[13]。Xu J等[14]利用KDE对实时寿命预测时参数的先验分布进行估计。Wang J[15]利用KDE对气缸故障时循环次数服从的概率密度进行估计。Zhang W等[16]基于时不变系统考虑了突变点检测的KDE剩余寿命预测。

针对以上问题,本文以疲劳齿轮为研究对象,采用时变系统基于KDE的剩余寿命预测方法,最终进行实例验证。

1 退化量分布的时变KDE

1.1 退化增量分布的时变KDE

根据时变系统中退化特征增量分布随时间变化而变化的特点,考虑引入时变权重的概念,分析样本时序性对KDE的影响,进而对剩余寿命预测准确性的影响。具体来说,随着时间的推移,距离当前时刻越近的样本点,越能反映当前退化系统的运行状态;反之,距离当前时刻越远的样本点,则对当前运行状态的影响越小。为了考虑时变权重的影响,在传统KDE模型的基础上引入时变权重因子,则t时刻的时变权重KDE可表示为:

(1)

式(1)中,T′为当前监测系统的寿命;K为核函数,由于核函数对密度之间平均积分均方误差(MISE,Mean Integrated Squared Error)的影响非常小,选择应用最为广泛的高斯核;wt,i为时变权重因子,根据历史样本ΔXi(i=1,2,…,t)与当前样本ΔXi间隔越大,对当前分布影响越小的规律,定义wt,i为:

wt,i=(1-ω)ωt-i,i=1,2,…,t

(2)

式(2)中,ω为遗忘因子,满足0≤ω<1,通过已知样本时变KDE的极大似然估计求得。

h为平滑窗宽,为避免实际采集的样本密度不均时固定平滑窗宽造成的过拟合或欠拟合问题,在初始h的基础上,根据样本密度引入局部窗宽因子,得到自适应窗宽:

(3)

因此,可进一步建立基于自适应窗宽的时变权重KDE模型:

(4)

1.2 实时递推更新

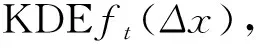
(5)

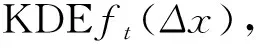
1.3 退化增量预测

由于时变系统中样本数据具有时序性,即距离当前越近的样本越能反映系统当前的运行状态,因此,本文利用指数加权移动平均(EWMA,Exponentially Weighted Moving Average)法对退化增量样本进行预测。

设t为当前时刻,则t时刻随机时间序列ΔXt的预测模型可表示成:

(6)

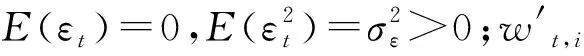
(7)

式(7)中,β为衰减因子(decay factor),满足0≤β<1[17].

在实际运行系统中,设t(t=1,2,…,T′)为当前时刻,则该时刻时间序列ΔXt的预测模型可表示为:

(8)

这样t之后任意时刻退化增量的预测值,都可根据历史样本的时间序列预测模型求得。

1.4 退化量分布的时变KDE

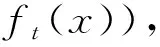
(9)

随着实时监测过程中退化量的不断变化,为减少重复计算,式(9)可以表示成递推的形式以提升时变KDE的计算效率:

(10)

2 实时剩余寿命预测模型

设当前寿命预测的机械系统其退化特征曲线示意图如图1所示。其中,设t为当前时刻,xth为失效阈值。

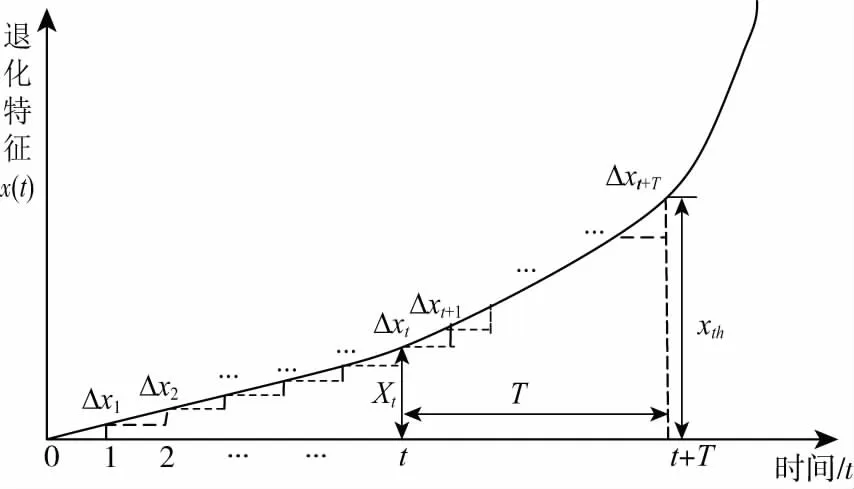
图1 退化特征曲线示意图Fig.1 Degraded characteristic curve diagram

设T为监测系统在当前时刻t的剩余寿命,则时变系统基于核密度估计的剩余寿命的概率分布Ft(T)为:

(11)

(12)

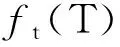
(13)

同理,监测系统实时运行中t时刻之后任意时刻的剩余寿命均可实现预测。

3 实例分析

试验数据采用图2所示的齿轮疲劳寿命试验台。其中齿轮箱中心距为150 mm,电机转速为1 200 r/min.试验对齿轮箱体的振动、噪声等信号进行监测,共布置8 个加速度传感器,其中,1#～4#位于主试箱轴承座径向,5#、6#位于陪试箱轴承座径向,7#、8#位于主试箱轴向,如图3、图4所示。试验恒载的方式进行,转矩为822.7 N.M.当试验齿轮发生断齿时即判定该齿轮失效。

图2 齿轮试验台架Fig.2 Gear test bench

图3 主试箱传感器位置图Fig.3 Sensors placement scheme of the main gearbox

图4 陪试箱加速度传感器位置图Fig.4 Sensors placement scheme of the accompany gearbox

由于均方根(RMS,Root Mean Square)在试验齿轮磨损退化过程中不受其个体差异的影响,不但能真实准确地反映齿轮的性能变化,而且易于计算。这里对4#的全部振动信号(2016组)进行特征提取。

监测信号的均方根可表示为:

(14)

式(14)中,Δt为采样时间,n为采样点数,满足n=Fs×Δt(Fs为采样频率),将采样点数换算为监测时间,则可得到均方根曲线图,如图5所示。

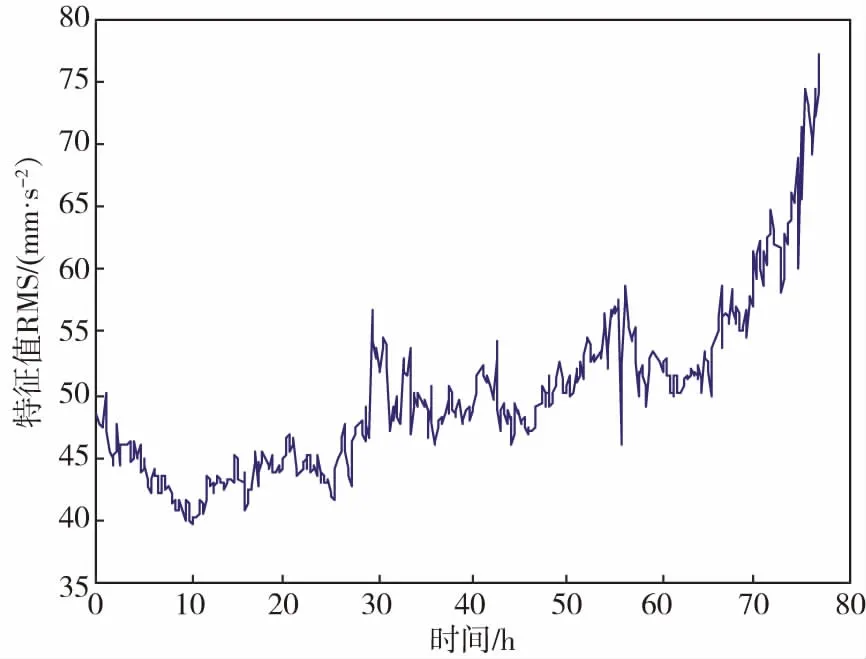
图5 RMS-MT变化曲线图Fig.5 RMS-MT change curve

由图5可看出,该变化曲线图为齿轮全生命周期曲线图。10 h之前齿轮处于啮合阶段;t∈[10,68]h时,齿轮正常磨损;68 h之后,磨损加剧,直至齿轮断齿失效。下面利用齿轮磨损试验样本数据,验证本文模型的合理性和有效性。

3.1 退化特征增量预测

由于时变系统中的参数随时间不断演化,因此要对剩余寿命进行较准确地估计,对未知的退化增量进行预测是必要的。图6为不同监测时刻,由EWMA法预测的退化增量值求得的均方根退化曲线图。

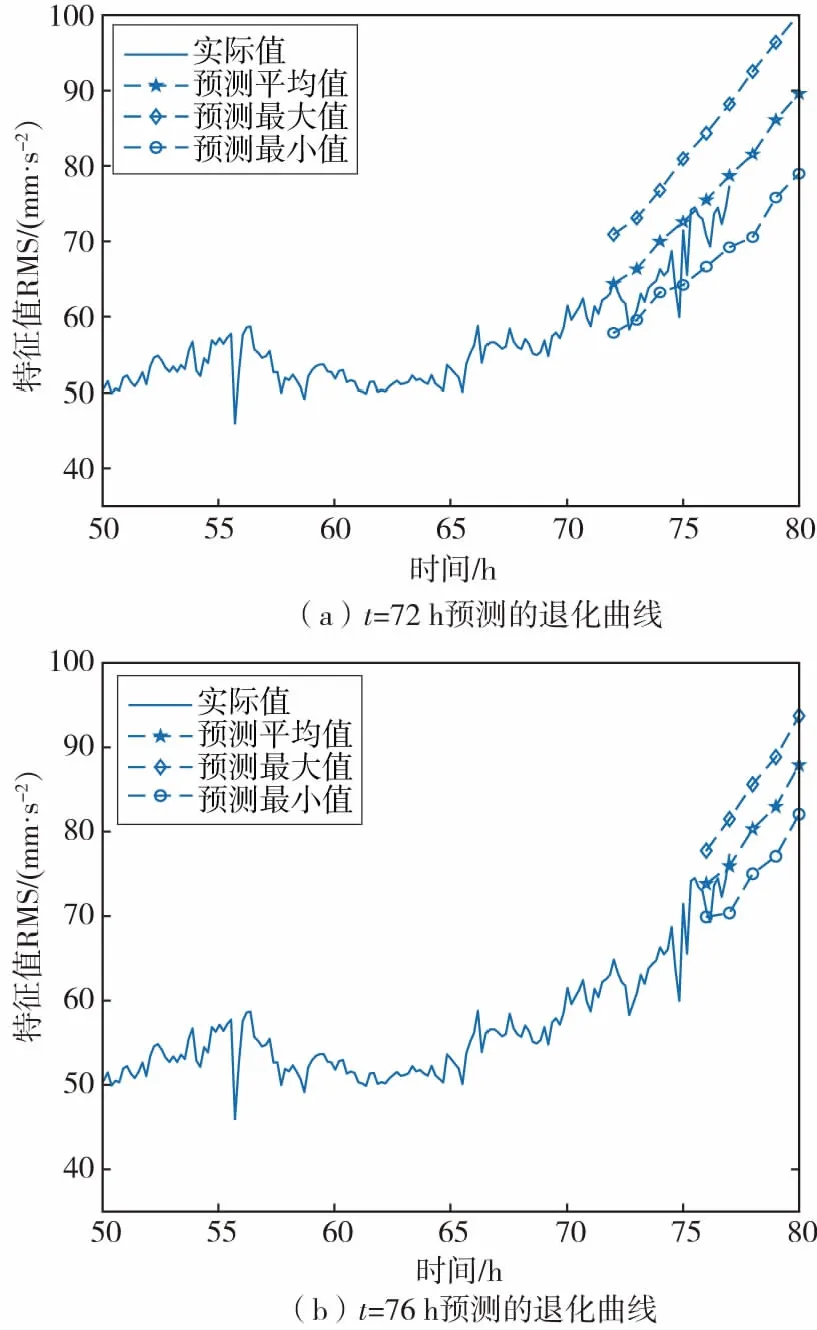
图6 不同时刻预测的退化曲线Fig.6 Degradation curves predicted at different times

由图6可看出,不同运行时间的均方根退化曲线预测图均有所差别。具体来说,在运行时间较短的时候,均方根预测曲线图与实际曲线图之间的误差较大。随着运行时间的持续增加,样本数据不断增多,均方根预测曲线图与实际退化曲线图之间的误差逐渐减小,直至接近实际的均方根退化曲线。从不同运行时间的均方根退化曲线,可以验证基于EWMA法预测退化增量值的适应性和有效性。

3.2 基于固定窗宽与自适应窗宽的MTTF比较

由于实际采集的样本数据密度分布不均,为提高剩余寿命预测中退化分布的准确性,根据实际采集到的样本数据分布自适应选择平滑窗宽,即样本数据分布密集的地方自适应选择较小窗宽,避免过拟合造成的密度估计不准确;反之,样本数据分布稀疏的地方自适应选择较大窗宽,避免欠拟合造成的密度估计不准确问题。

表1给出了不同运行时间两种窗宽下基于本文模型预测的剩余寿命概率密度的平均故障时间(MTTF,Mean Time To Failure)比较结果:

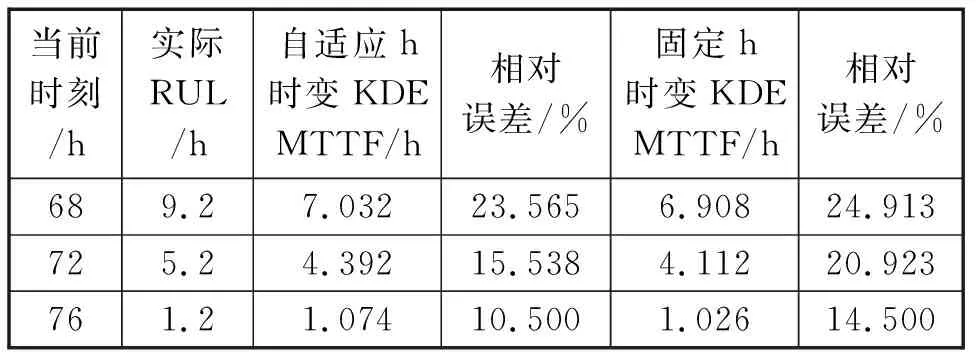
表1 两种方法的预测结果比较Tab.1 Comparison of prediction results of two methods

(15)

从表1的比较可看出,随着运行时间的增加,两种窗宽下预测的MTTF与实际剩余寿命之间的误差均逐渐减小,且从计算的误差结果显示,基于自适应窗宽方法的预测结果与实际剩余寿命之间的误差更小。

3.3 基于KDE的剩余寿命概率密度比较

图7给出了时变系统不同运行时间基于本文模型的实时剩余寿命预测结果。

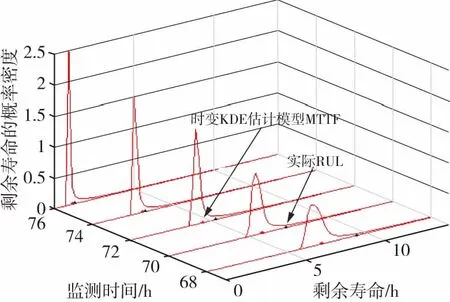
图7 不同监测时刻RUL的概率密度Fig.7 Probability density of RUL at different monitoring times

通过图7中不同运行时间预测的平均剩余寿命与实际剩余寿命的比较可以看出,随着运行时间的持续增加,预测的平均剩余寿命与实际剩余寿命之间的误差逐渐减小,同时,预测的剩余寿命概率密度曲线不断变窄,说明方差逐渐减小,从而验证了本文模型的有效性。

3.4 本文方法与基于Kalman滤波预测结果的比较

由于Kalman滤波从统计角度预测实时剩余寿命,预测结果优于当前许多寿命预测方法。因此,为进一步验证本文方法的合理性,与基于Kalman滤波状态空间模型方法的预测结果[18]进行了比较,结果如表2所示。

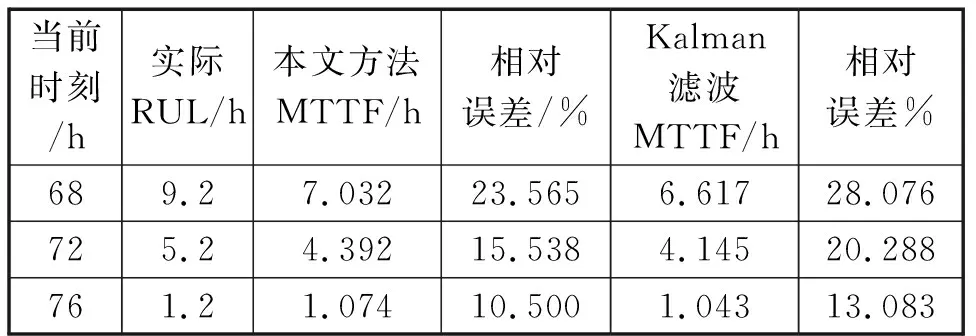
表2 两种模型的预测结果比较Tab.2 Comparison of prediction results of the two models

从表2可以看出,与基于Kalman滤波的实时剩余寿命预测结果相比,本文方法不同时刻的预测结果与实际剩余寿命之间的相对误差更小,说明本文方法的预测性能更优。

4 结论

实际运行的系统往往都是时变系统,本文以时变系统为研究对象,针对实际运行中自身样本数据不够,同类系统故障样本数据缺少导致的剩余寿命预测时模型结构假设不够准确的问题,提出了一种基于KDE的实时剩余寿命预测模型。根据样本数据与当前时刻的距离不同,分别在样本数据的核密度估计过程中赋予不同的权重。具体来说,距离当前时刻越近的样本赋予越大的权重;距离当前时刻越远的样本则赋予越小的权重。同时,由于时变系统中的参数随时间不断演化,根据样本的时序性利用EWMA法对其未来的样本进行预测。另外,由于实时运行过程中,样本数据不断增多,建立时变系统基于KDE的递推更新模型,减少密度估计中不必要的重复计算。最后,通过实际齿轮箱体监测数据验证了本文方法的有效性和竞争性。