基于改进麻雀算法的分布式电源优化配置
陈 旺,潘 峰,2
(1.太原科技大学 电子信息工程学院,太原 030024;2.茅台学院酿酒工程自动化系,贵州 仁怀 564507)
分布式电源(Distributed Generation,DG)因其安全可靠性高、提高能源利用率等优点,近年来在电网中逐渐普及。随着DG接入规模越来越大的同时会引发配电网出现一些问题。首先,DG的接入会使得配电网中线路潮流方向和大小变得复杂化。其次,大规模的DG接入会使电网系统电压偏移增大,影响其安全性[1]。当配电网中的分布式电源系统配置合理时,会使得配电网网损降低、电压质量升高和降低配网投资成本,保障系统的安全运行。
国内外学者已经对分布式电源各方面问题的优化配置进行了一系列的研究。文献[2]主要是以经济性最佳对分布式电源进行选址,并以网损改善率和电压稳定度为指标考量对其优化选址的意义;文献[3]是以多个目标对分布式电源进行优化,包括配网网损、电压偏移以及电压稳定度;文献[4]是从不同的DG的类型、接入位置和容量、优化目标等多个角度对分布式电源进行优化配置,并且用二阶锥松弛和Big-M方法进行求解验证以上各个角度对含有DG配电网会有重要影响。
根据上述文献所研究内容,本文提出了分布式电源规划模型。并且在模型求解方面提出了一种改进的麻雀算法(SSA),将其应用于分布式电源选址定容的优化中,并最终使得配电网整体的经济效益最优。
1 分布式电源优化配置模型
1.1 目标函数
配电网的年综合成本最小为目标函数建立数学模型[5]。
目标函数:
minFTotal=CIN+COM+CBU+CLOSS
(1)
式中:FTotal为配电系统的年综合成本,包含了下述4类成本:
(1)DG的年折算后安装投资成本CIN
CIN=αDG*γDG*EDG
(2)
(3)
式中:αDG为DG的折算系数;rDG为DG的贴现率;TDG为DG的设计寿命;EDG为安装DG的容量;γDG分别为DG安装成本。
(2)DG的年折算后运行维护成本COM
COM=Cmai.dg*EDG
(4)
式中:Cmai.dg为分布式电源单位容量维护成本。
(3)网损成本CLOSS
CLOSS=CP*TLOSS*PLOSS
(5)
式中:CP为日平均电价,TLOSS为最大负荷损耗小时数,PLOSS为损耗的电量。
4)主网购电成本CBU
CBU=(PTOTAL-PDG*0.9)CP*TMAX
(6)
式中:PTOTAL为配网负荷总量,TMAX为年最大负荷利用小时数,PDG为分布式电源输出的电量。
1.2 约束条件
模型的等式约束及不等式约束如下:
(1)DG的容量约束
(7)
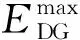
(2)节点电压约束
Uimin≤Ui≤Uimax
(8)
式中:Uimax、Uimin分别为电网标准规定的电压波动的上下限,为93%UN~107%UN.
通过罚函数法可保证种群个体尽可能满足约束条件。含惩罚项目标函数可用下式表示:
λ2{Ui-Uimax,0}+λ3{Uimin-Ui,0}
(9)
式中:λ1、λ2、λ3分别为惩罚因子。
2 麻雀算法
2.1 麻雀算法优化机理
麻雀搜索算法(Sparrow Search Algorithm,SSA)是由薛建凯于2020年首次提出的一种新型智能优化算法[6]。该算法通过模拟麻雀种群的觅食和反哺食行为来实现问题的优化求解。在该算法中主要有三个角色,分别为发现者、加入者、捕食者,且发现者、加入者两者身份可随时转换。其中发现者相当于是整个种群的头脑,负责为所有的加入者指引觅食的区域及方向。整个种群中个体麻雀的能量越低,它所在的觅食区域便是不够好,所以它的适应度就越差,此时它们就需要去更好的区域以补充能量。在种群中,发现者总是处于觅食效果最好的区域,加入者总是追随着发现者以获取更好的区域。种群个体在遇到危险即捕食者时,发出预警,边缘个体迅速向更好的区域移动,而区域中心其他麻雀个体则是随机移动寻优。
2.2 麻雀算法数学描述
假设麻雀种群个体数为N,需要优化的目标维数为D,则该种群可表示为下式:
(10)
该种群的适应度如下式所示:
(11)
式中:f表示适应度。
(12)
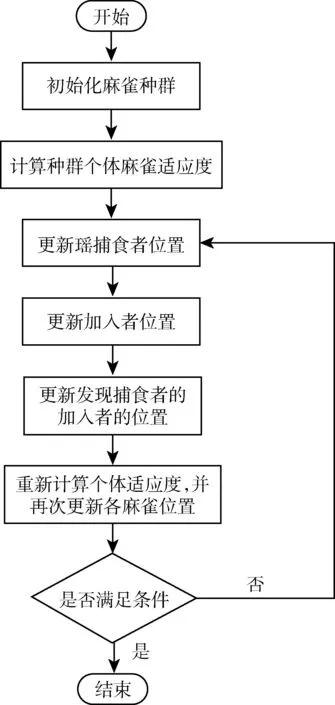
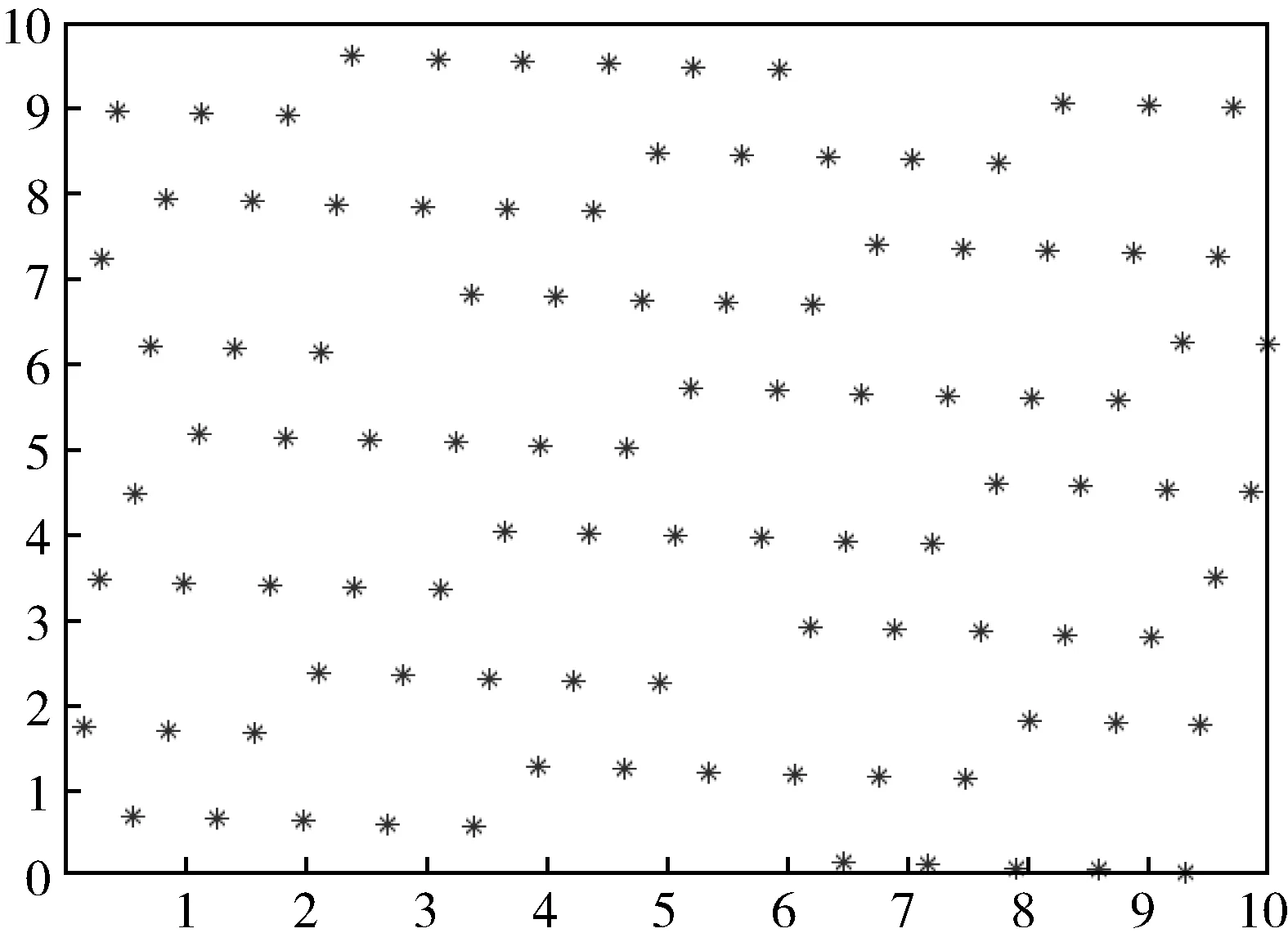
式中,t为当前迭代次数;itermax表示最大迭代次数。Xij表示第i个麻雀的j维位置信息。α为0到1的随机数;Q为正态分布的随机数;L为1行d列的单位阵;R2 在SSA中,发现者总是处于觅食效果最好的区域,其位置可由下式表示: (13) 在麻雀种群中,可以意识到以上情况的麻雀初始种群数量为10%到20%,麻雀初始种群随机产生,然后按照以下公式更新位置。 (14) 虽然SSA局部搜索能力极强且收敛速度快,但是全局搜索能力较弱且容易陷入局部最优。在此,通过改变麻雀算法中初始种群的分布,以此来增大算法的搜索范围避免陷入局部最优。在SSA中,其初始种群是随机产生的,以这样的方式产生的初始种群粒子分布极不均匀,算法很容易陷入局部最优,甚至不收敛。因此,本文通过使用佳点集法产生麻雀种群的初始种群粒子,对其进行初始化,以此来获得种群粒子均匀且不重复的初始种群[8]。 佳点集法初始种群粒子的具体步骤为: S1:令麻雀算法初始种群维数为D,麻雀种群数量为N,则有: rj=ej,1≤j≤D (15) S2:以S1为基础,则佳点集中第i个j维的初始粒子可表示为: rij=irj-⎣irj」,1≤j≤D,i=1,2,3,…,N (16) S3:将佳点集映射到问题的可行域,第i个麻雀的的j维的粒子可表示为: xij=lj+rij(uj-lj),1≤j≤D,i=1,2,3,…,N (17) 式中:uj、lj分别为每个麻雀个体第j维的上限和下限。 将使用随机法与佳点集法在2维空间生成的初始种群粒子分布进行对比,麻雀种群数量为100.从图3、图4可以看出,随机法生成的初始种群粒子分布不均匀,且存在有重复的个体,而佳点集法与之相反,故其产生的麻雀种群更有利于算法的全局寻优。 图1 麻雀算法优化配置流程图Fig.1 Flow chart of SSA optimization configuration 图2 随机法初始种群粒子分布Fig.2 Particle distribution of initial population by random method 图3 佳点集法初始种群粒子分布Fig.3 Particle distribution of the initial population by the good point set method 图4 DG接入配电系统后各节点电压的变化曲线Fig.4 Voltage change curve of each node after DG is connected to the power distribution system 通过改进麻雀算法对分布式电源进行优化配置算法流程图如图1所示。 具体计算步骤如下: S1:用佳点集法初始化种群,设置迭代次数,设置加入者、捕食者比例。 S2:计算种群个体麻雀适应度,并排序。 S3:更新捕食者位置;更新加入者位置。 S4:更新发现捕食者的加入者的位置。 S5:重新计算种群各个个体适应度,并再次更新各麻雀位置。 S6:判断是否满足条件,满足则退出,并输出结果,否则返回S2. 本文是在标准的IEEE33节点系统中进行算例仿真与分析,以验证本文所提出的模型的可行性和有效性。并且设置分布式电源总体渗透率为20%. 初始化改进麻雀算法参数设置如下。麻雀种群大小N=100,可意识到自身“危险”麻雀个体数量为20.表1为DG相关参数: 表1 DG的相关参数Tab.1 Related parameters of DG 将前文中所提出的优化模型在MATLAB软件中仿真分析,用文中改进后的麻雀算法(SSA)求解后,优化后各节点电压与网损的对比图如图4、图5所示。 图5 DG接入配电系统后各支路损耗的变化曲线Fig.5 The change curve of the loss of each branch after DG is connected to the power distribution system 然后将用粒子群算法(PSO)、麻雀算法(SSA)、改进麻雀算法(改进SSA)三种算法求解模型后的DG配置结果对比图如表3所示,优化后最低电压对比如表2所示[9]。由表中数据可得,利用本文所提出的改进麻雀算法对DG进行优化配置可以有效减小配电网的投资成本,并且减小网络损耗,改善电压质量。并且本文所提出改进麻雀算法效果稍优。 表2 不同算法优化后电压对比Tab.2 Voltage comparison after optimization of different algorithms 表3 不同算法优化结果对比Tab.3 Comparison of optimization results of different algorithms 本文对于麻雀搜索算法(SSA)的改进主要是对其容易因初始种群的随机性而陷入局部最优的情况进行改进。粒子群算法(PSO)、麻雀算法(SSA)、改进麻雀算法(改进SSA)三种算法优化配置的收敛曲线如图6所示。 图6 不同算法优化配置的收敛曲线Fig.6 Convergence curves of different algorithm optimization configurations 由图可以看出,三种算法以改进麻雀算法(改进SSA)的收敛速度最快,并且由图可以看出粒子群算法(PSO)在迭代次数4次到24次差点陷入局部最优的情况,使其收敛速度慢于麻雀算法(SSA).所以,本文所提出的改进麻雀算法(改进SSA)具有一定的有效性。 本文所建立的分布式优化模型,以DG经济效益最优为目标,在模型求解方面提出了一种改进的麻雀算法(SSA),并在IEEE33节点系统中仿真验证了本文所提出模型的可行性。在配电网中对分布式电源进行优化配置,可以有效减小配电网的投资成本,并且减小网络损耗,改善电压质量。最后,本文对麻雀算法(SSA)的改进方法效果很好。
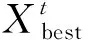
2.3 麻雀算法改进


3 算法流程
4 算例仿真分析
4.1 计算参数
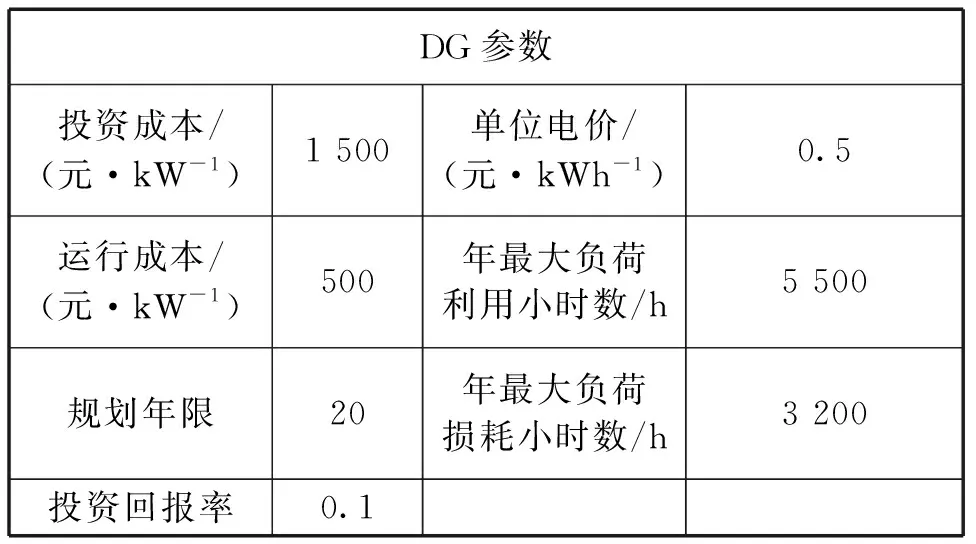
4.2 仿真结果分析


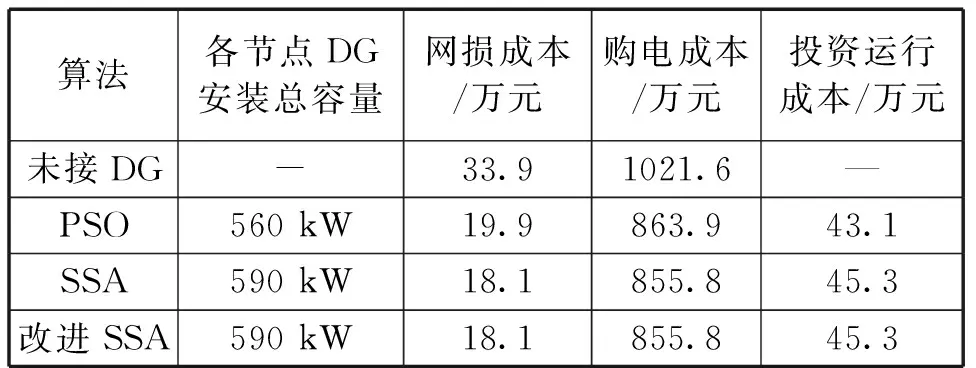
4.3 各算法收敛效果对比
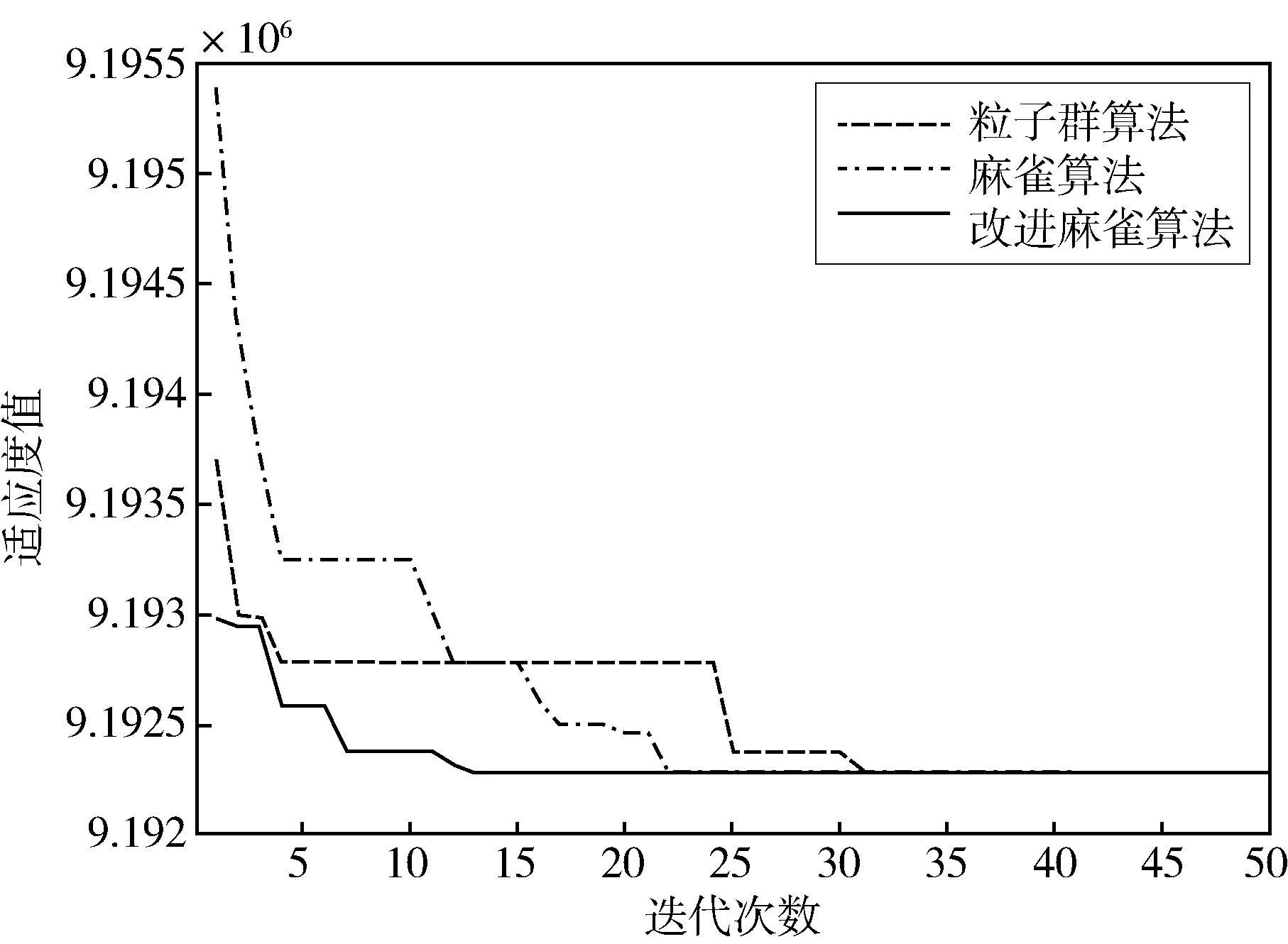
5 结论

