基于动态贝叶斯网络的轴承故障在线诊断方法

王泽渊,宋仁旺,石 慧

(太原科技大学 电子信息工程学院,太原 030024)

滚动轴承故障会引起机器产生异常振动和噪声,加速机器损坏,甚至引发人员伤亡等重大事故,因此研究轴承的故障监测与诊断具有重要的意义[1]。贝叶斯网络(Bayesian networks,BN)在故障诊断领域已经得到广泛的应用。Chen等[2]应用贝叶斯网络理论,建立了风力发电机加速齿轮箱的故障诊断模型。张露江等[3]在分析了贝叶斯网络全概率公式的基础上搭建了以广义逆矩阵为核心的智能诊断系统,智能诊断结果和人工诊断结果相符。贝叶斯网络是一个有向无环图,它反映了一系列变量间的概率依存关系,没有考虑时间因素对变量的影响[4]。动态贝叶斯网络(Dynamic Bayesian Network,DBN)可以在概率框架下实现动态和静态信息的融合,适合对既具有特征相关性又具有时序相关性的复杂过程进行建模。

DBN模型可以对动态变化的过程进行跟踪和描述。Kammouh等[5]采用DBN模型处理工程系统各观测指标之间的关系,该方法可以跟踪系统的性能演变,能在给定初始条件下预测系统的状态。Qian等[6]建立了传感器网络的DBN,利用马尔可夫链得到测量传感器的可靠性随时间的退化情况,该方法能够定量地分析由不同传感器组成的检测传感器网络在给定时间段内的可靠性。刘东[7]等在构建故障诊断模型时,需要引入专家知识确立网络节点之间的连接关系,模型建立对专家知识的依赖程度较高。王承远等[8]建立基于DBN的故障诊断模型时,每个时间片中的网络节点是相互独立的,忽视了单个时间片中网络节点之间的相关性。王双成等[9]在建立DBN模型时虽然考虑了每个时间片中变量的相关性,但是其网络结构在所有时间片上是相同的,即观测变量之间的依赖关系在时间维度上是不变的。而机械设备发生故障后,监测的振动信号是时变非平稳的,且观测变量的依赖关系在不同状态下(不同的故障类型或者同种类型故障不同的程度)的依赖关系会发生改变,因此相邻时间片或者不同时间片的观测变量依赖关系会产生差异,产生不同的网络拓扑结构,从而每个时间片下的概率分布是不同的;再者不仅相邻时间片之间的观测状态存在依赖关系,同一观测变量在相邻时间片上也存在依赖关系[10]。

本文利用历史故障数据,将轴承的运行过程划分为正常阶段、轻微阶段、严重阶段和最终失效阶段。在故障的不同时期,故障特征的依赖关系是不同的,自适应选择不同的网络拓扑结构描述故障特征的相互依赖关系。非正常阶段反映了设备的退化速度和性能退化趋势,由于反映故障特征的状态变量在一定范围内波动反复,非线性变化,采用DBN模型的状态转移描述故障过程的波动性。然后使用历史数据学习网络参数,建立轴承在线监测和诊断模型。当实时传感器数据输入网络时,首先评估轴承运行状态是否正常,如果运行状态不正常则进一步判断轴承故障的类型。在实时监测诊断系统中,已判断的轴承状态信息可以重复使用,减少重复计算,提高诊断的实时性。最后进行仿真实验,验证模型的有效性。

1 动态贝叶斯网络

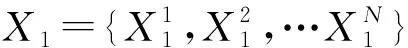
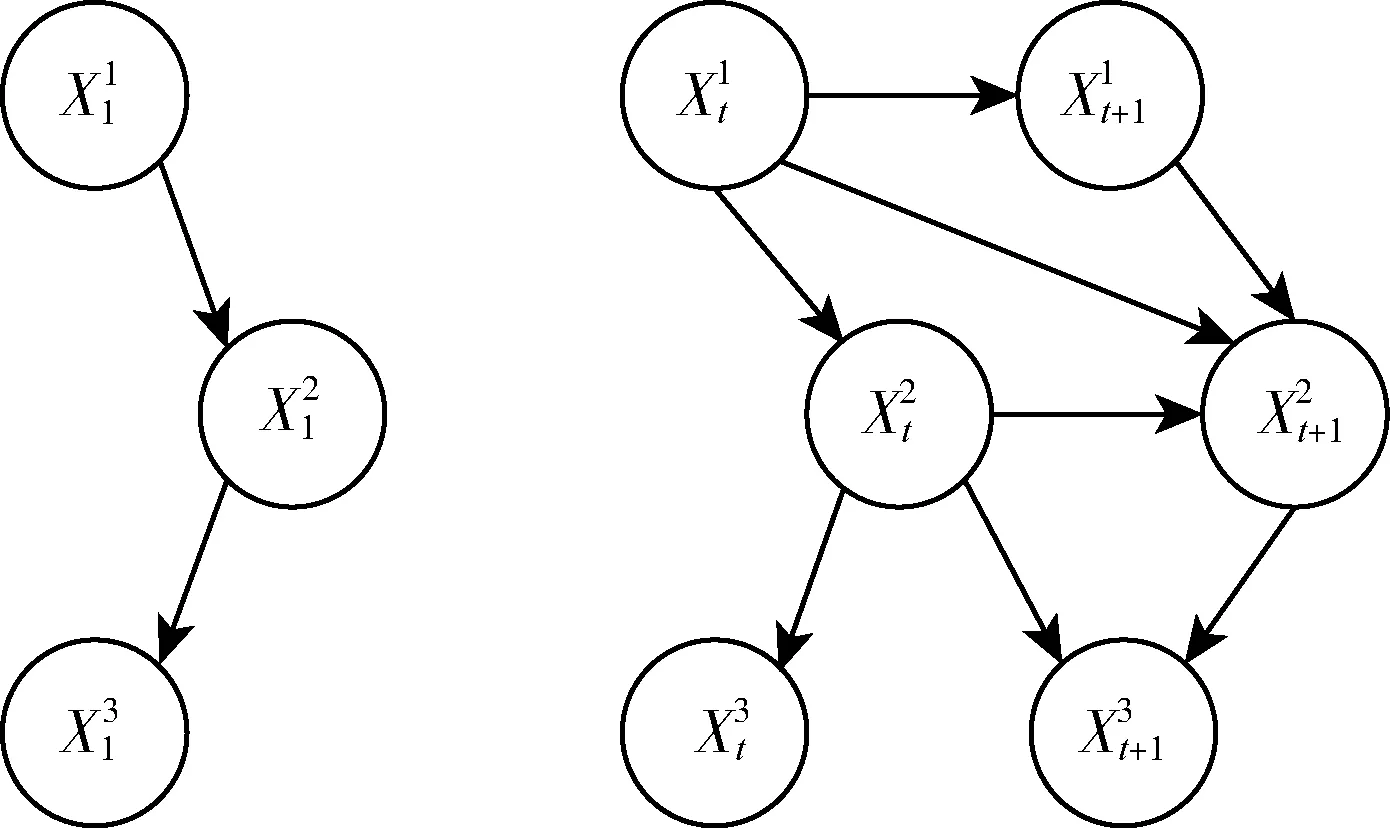
图1 DBN先验网和转移网Fig.1 Dynamic Bayesian Network prior network and transfer network

在实际应用中,一般只考察有限时间段1,2,…,T,完整DBN拓扑结构如图2所示:在初始时刻1,X1中节点的父节点是在先验网B1中的节点;在时刻t(t=2,3,…,T),Xt中节点的父节点是在t时刻或者t-1时刻中与Xt相关的节点。

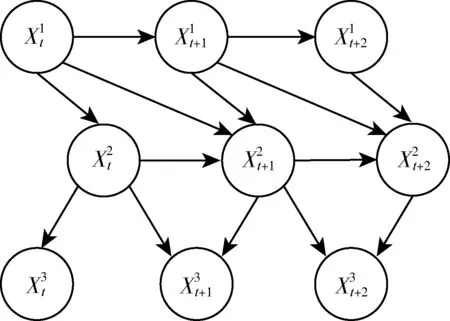
图2 动态贝叶斯网络结构图Fig.2 Dynamic Bayesian Network structure diagram

给定一个DBN模型,变量集X1,X2,…,XT上的联合概率分布为:

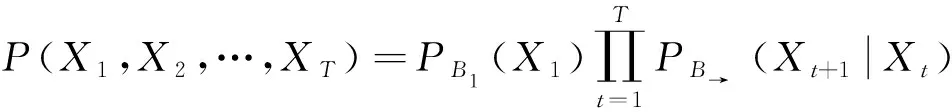
(1)

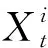
(2)

DBN在前T个时间片的联合分布[12]为:

(3)

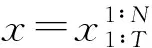
c*(x)=max{P(ci|x)}

(4)

依据贝叶斯公式:

(5)

2 动态贝叶斯网络模型的建立

2.1 建立DBN网络结构

滚动轴承失效劣化过程通常是一个随时间递进的过程,目前工业界将其演化过程大致分为4个阶段,如图3所示,分别是正常阶段、轻微阶段、严重阶段和最终失效阶段。

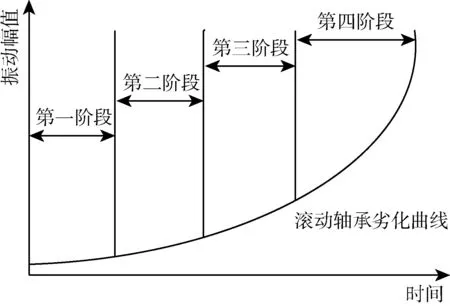
图3 滚动轴承失效劣化过程Fig.3 Rolling bearing failure degradation process

为了更加精准地描述故障过程中变量的相互依赖关系以及轴承状态的变化过程,本文的DBN拓扑结构S采用三层离散DBN,网络结构如图4所示:

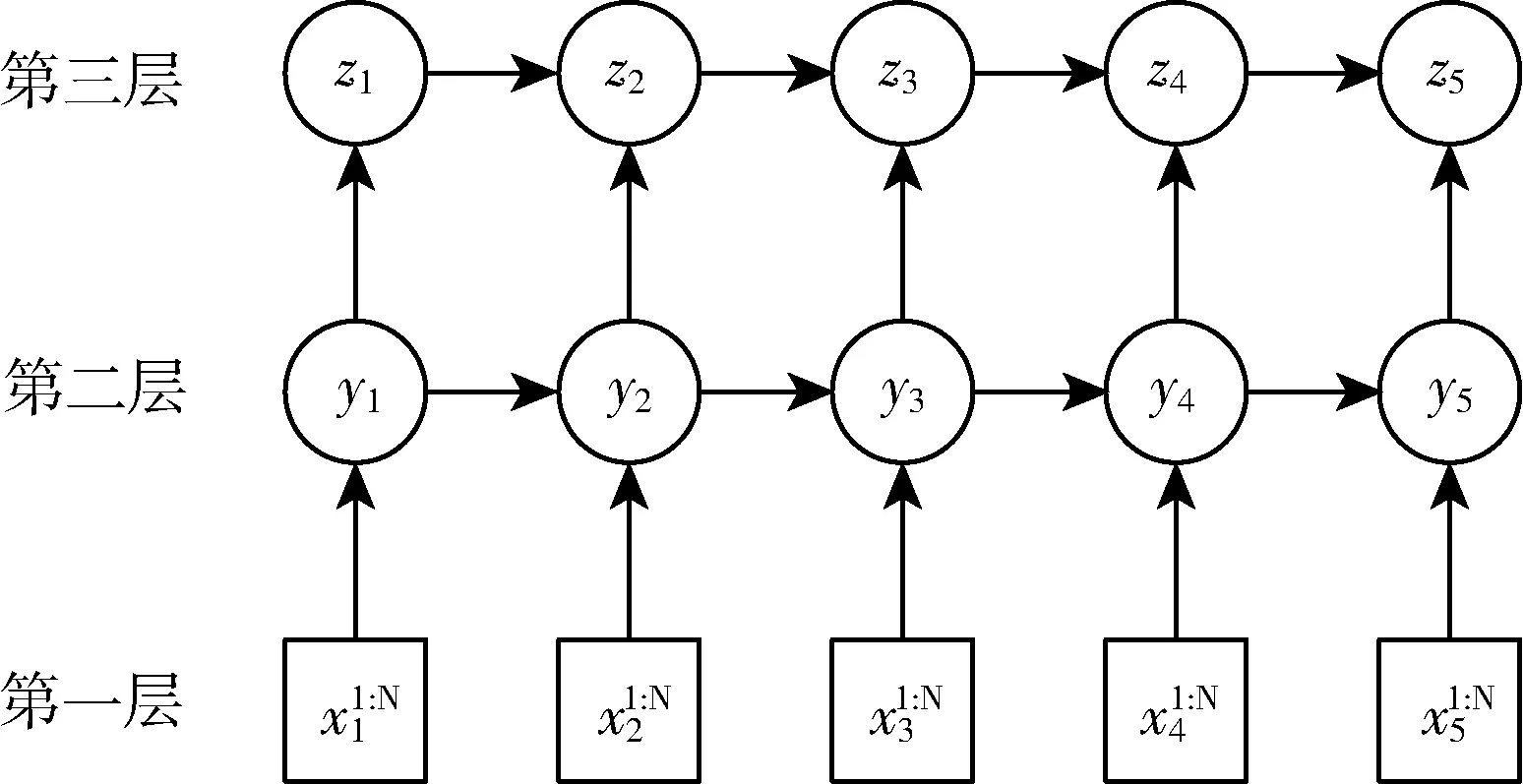
图4 DBN故障诊断模型Fig.4 DBN fault diagnosis model

第一层是观测变量层,在已知当前时刻的监测数据时,观测变量是确定的。采用贝叶斯网络对观测变量Xt进行判断,输出当前时刻的隐状态yt(yt∈{y1,y2,…}),并且结合历史时刻的隐状态yτ(τ=1,2,3…t-1)组成状态序列Y={y1,y2,…yt}.网络的第一层表示观测变量和隐状态的联合概率关系,且不同隐状态下观测变量对应的网络结构是不同的。而对于DBN第一层网络的拓扑结构,本文采用基于依赖分析的方法建立网络拓扑结构。

第二层是隐状态变量层,第二层对隐状态序列Y={y1,y2,…yt}进行解码处理,输出状态序列Z={z1,z2,…zt},其中相邻时间片的联合概率采用隐状态转移概率连接。

第三层是决策层,根据状态序列Z综合判断轴承的运行状态,如果轴承发生故障,进一步进行故障在线诊断。在DBN模型的第二层与第三层,允许状态变量状态循环,描述故障过程的状态波动。在应用中,可以为第二层和第三层网络赋予不同数量的状态空间数目。

2.2 学习DBN的网络参数

DBN网络参数的学习是模型建立的重要环节,本文网络采用分层学习的方法,采用两种不同的学习策略对网络的参数进行学习。

对于DBN第一层网络参数的学习,在上述建立网络拓扑结构的基础上,采用样本统计学习的方法进行网络参数的学习,即学习P(Y|X,S).

对于第二层网络,DBN的参数θ={A,B}包括两部分,其中A表示隐状态y的初始分布,B表示隐状态y的状态转移矩阵。为了方便学习参数,DBN作如下假设和简化处理。

(1)假设在有限的时间内(每一个时间片内),条件概率变化过程对所有的t是一致平稳的;

(2)假设动态概率过程是满足马尔可夫性,即未来时刻的概率只与当前时刻有关,与之前时刻无关:

P(Xt+1|X1,X2,…,Xt)=P(Xt+1|Xt)

(6)

(3)时齐性假设,假设相邻时间片状态转移概率与状态转移发生的时间点没有关系,即对于任意时刻t1,t2有:

P(Xt1+1|Xt1)=P(Xt2+1|Xt2)

(7)

若已知观测序列集合X和结构S,在t时刻隐含状态变量Y从状态i转移到状态j的条件概率为:

ξt(i,j)=P(yt=i,yt+1=j|X,S)=

(8)

在t时刻隐含状态变量y是状态i条件概率为:

(9)

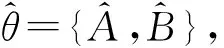
(10)

(11)

2.3 DBN在线监测和诊断

在线监测数据ot输入网络,计算到当前时刻为止系统的最优状态序列Y:

定义δt(i)为在时刻t隐藏状态y=i所有可能的状态转移路径i1,i2,…,it中的概率最大值。

δt(i)=

(12)

δt+1(i)=

(13)

定义在时刻t隐藏状态为i的所有单个状态转移路径(i1,i2,…,it-1,it)中最大转移路径中第t-1个隐藏状态为Ψt(i):

(14)

有了上述两个局部状态,就可以从时刻t=1一直递推到时刻t=T,然后利用Ψt(i)记录的前一个最可能的状态节点反向推导,直到找到最优的隐藏状态序列。

上述算法求出的最优状态序列并不一定是描述系统状态的最优序列,采用指数加权移动平均法(EWMA)的方法对状态序列进行优化,最后做出诊断决策。

EWMA算法如下:

zt=α·zt-1+(1-α)·yt

(15)

yt是t时刻的观察值,zt是t时刻的EWMA值,系数α表示权值下降速度,α值越小下降速度越快。

在t=0时刻,初始化z0=0.EWMA表达式归纳为:

(16)

3 实验方案及分析

3.1 实验方案

仿真实验平台为Windows10系统,处理器为i5 2.4GHz,平台软件为Matlab R2016a,实验数据使用XJTU-SY滚动轴承加速寿命试验数据集[13]。滚动轴承实验平台如图5所示,实验台平台由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承等组成。试验中设置采样频率为 25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s.

图5 滚动轴承实验平台Fig.5 Rolling bearing test platform

采集的原始加速度信号如图6所示,横坐标表示采样时间点,纵坐标表示幅值大小,单位是重力加速度g.

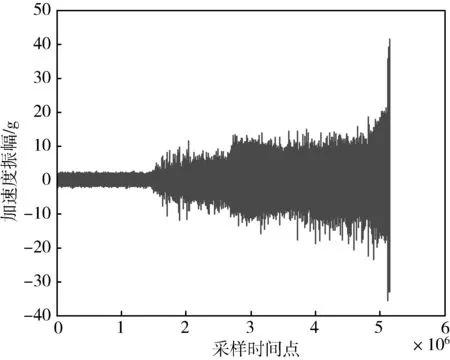
图6 滚动轴承故障状态初始加速度信号Fig.6 Initial acceleration signal of rolling bearing fault state

所选取的原始实验数据包含滚动轴承的正常状态和3种不同类型的故障状态,故障状态分别是内圈故障、外圈故障和滚动体故障,4种状态分别定义为正常状态、故障类型1、类型2和类型3.4种状态每种状态选择160个样本,每个样本包含相邻10个采样周期的数据,每种状态选取100个样本作为训练集,60个样本作为测试集,具体如表1所示。同时按照轴承劣化状态对每类故障分成三个故障时期,分别对应轴承劣化曲线的第二、三、四阶段。

表1 轴承样本数据Tab.1 Bearing sample data

文献[14]计算故障样本的17维故障特征,然后使用皮尔逊相关系数法去除冗余的特征,选择最能区分故障的故障特征进行网络拓扑结构的确立,降低模型的复杂程度。消除冗余属性后最终保留了9个特征属性。

首先根据依赖分析的算法,建立动态贝叶斯网络拓扑的第一层;在不同故障的不同发展时期,故障特征节点之间的依赖依赖关系会发生改变,采用依赖分析的方法自适建立网络拓扑结构,表示故障发生时各故障特征的相关关系。

图7是内圈故障在第二、三阶段特征属性的条件依赖关系图,表示在轴承内圈故障的不同发展时期,特征属性的依赖关系会发生变化。动态贝叶斯网络拓扑结构建立以后,使用标记数据统计计算故障症状与故障隐状态的条件概率分布表。

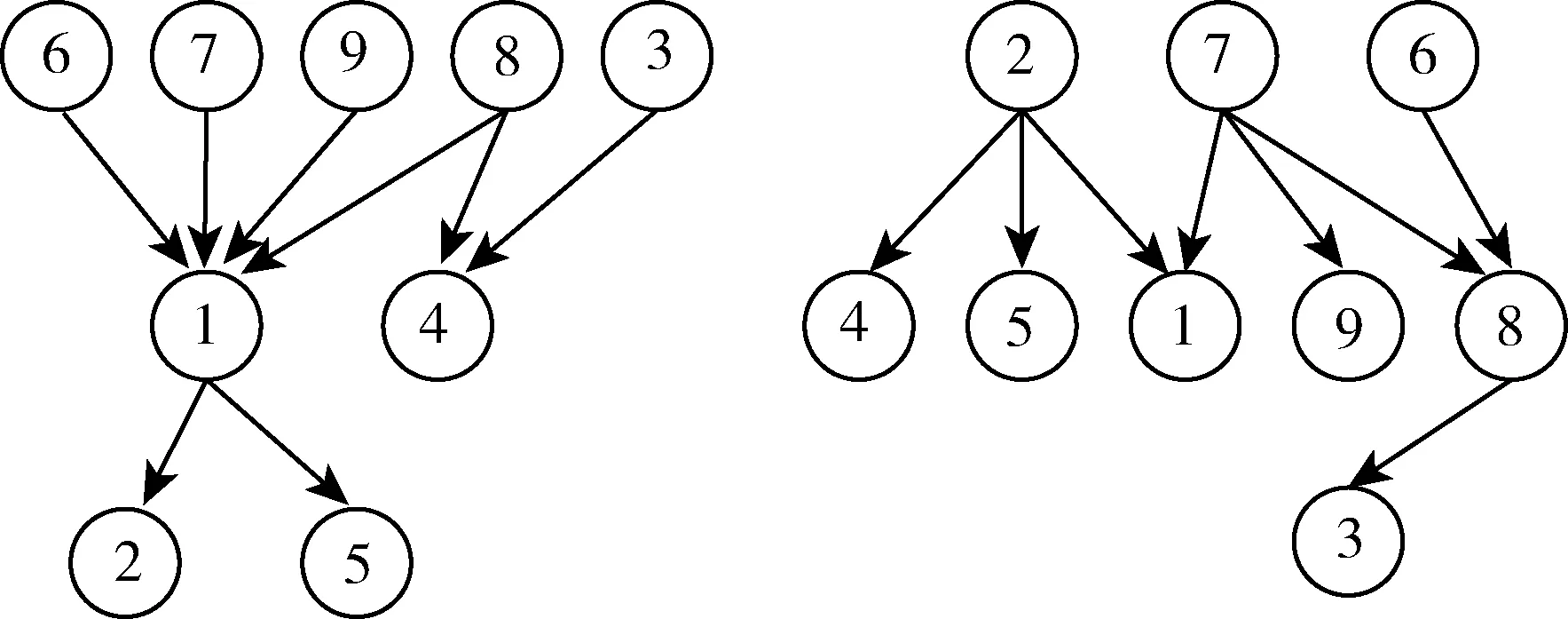
图7 第一层DBN的部分拓扑结构Fig.7 Part of the topology of the first layer of DBN

网络的第二层根据第一层的结果,判断故障所处的故障状态,生成表示故障状态的隐状态序列,隐状态序列中包含故障前后时间片的之间影响。隐状态之间的状态转移矩阵采用EM算法进行最大似然估计。

对于网络的第三层,根据网络的隐藏状态推导出反映系统状态的序列。对第二层网络的输出序列进行指数加权移动平均,进一步优化状态序列的,最终根据优化的状态序列进行故障诊断决策。

3.2 实验结果分析

表2是使用DBN方法进行故障诊断的的混淆矩阵,可见网络可以对正常状态和故障状态进行区分,并进一步判断故障类型。

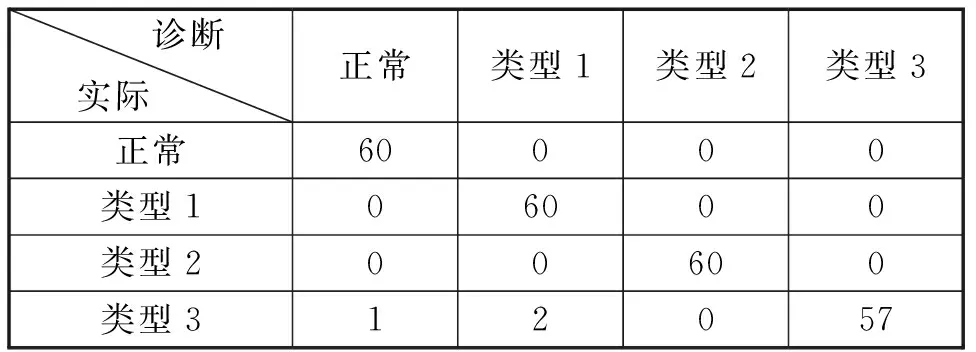
表2 DBN方法故障诊断的混淆矩阵Tab.2 Confusion matrix of DBN method fault diagnosis

图8是测试数据分别使用BN、CNN和DBN方法进行故障诊断时故障的诊断准确率。表明使用DBN方法比使用BN方法有更高的故障诊断准确率,使用BN方法和CNN方法的平均诊断准确率为97.08%、97.00%,DBN方法的平均故障诊断准确率为98.75%,平均诊断准确率提高了1.67和1.75个百分点。

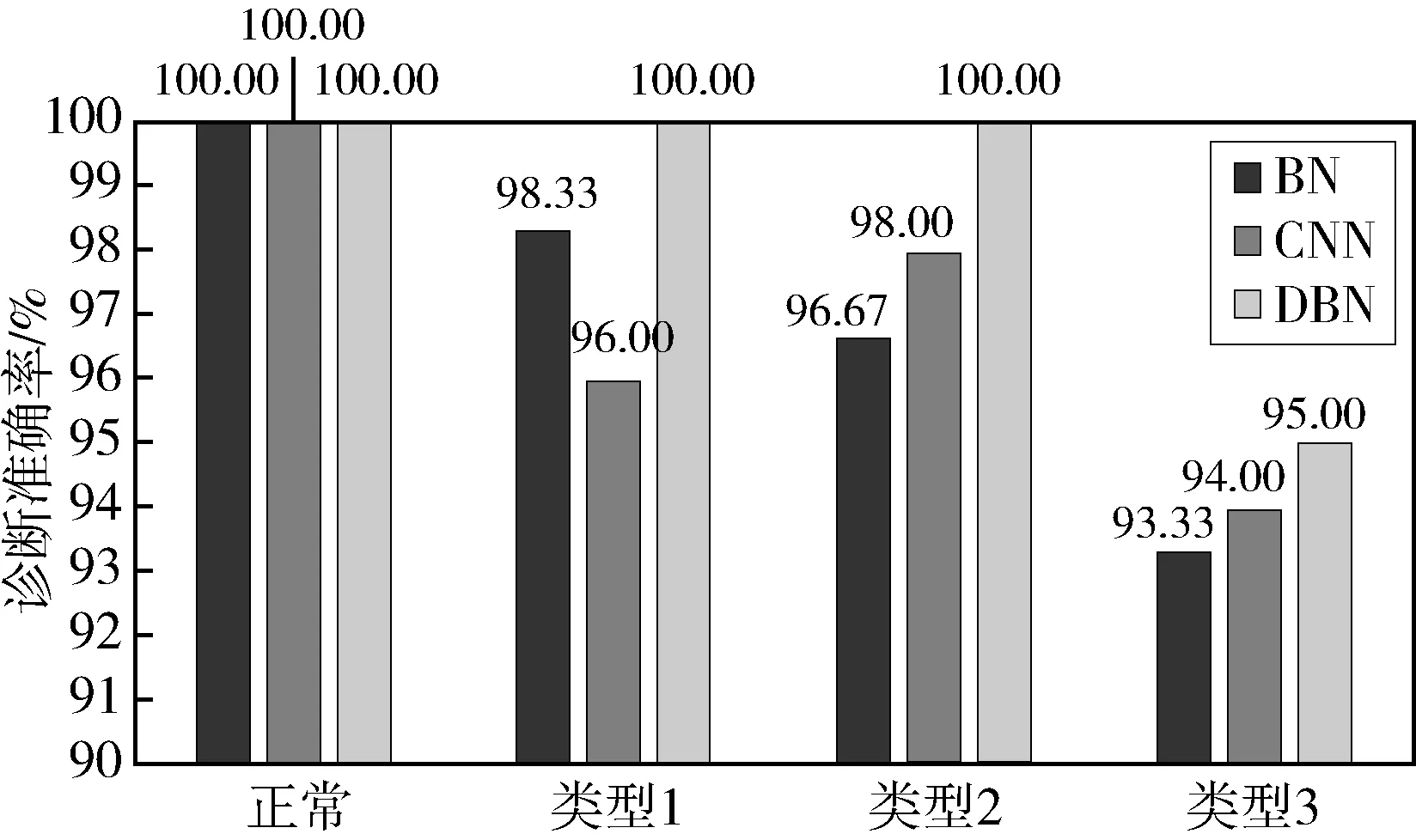
图8 本文方法和参考文献方法的比较Fig.8 Comparison of the method in this article and the method of reference

引入故障诊断率(Detection Rate,DR)和误报警率(False Alarm Rate,FAR)这两个评价指标,对应的方程如下所示[15]。最后计算得到各方法诊断结果如表3所示:

表3 各方法DR和FAR的比较Tab.3 Comparison of DR and FAR of each method

(17)

(18)

式中:TN表示故障状态被诊断为故障状态,FP表示故障状态被诊断为正常状态,FN表示正常状态被诊断为故障状态,TP表示正常状态被诊断为正常状态。

由表3本文方法可以有效识别轴承的正常状态和故障状态,故障诊断率为99.58%,而传统的SVM和BP网络的DR值为88.50%和82.15,远低于本文方法;并且本文方法不会将正常状态诊断为故障状态,误诊率为0,与CNN与BN方法的误诊率持平,而基于传统的SVM和BP网络方法误诊率较高;综合图8,本文方法不仅有较高的故障诊断率,并且可以对故障状态进行进一步分类,能够实现滚动轴承的故障诊断。

4 结论

本文提出了基于动态贝叶斯网络的轴承故障在线诊断方法。通过将不同类型的故障划分成不同的故障阶段,更加准确地描述了轴承故障状态的变化,实现使用实时数据对轴承进行在线监测和诊断。通过该方法进一步提高静态贝叶斯网络的诊断准确率,为机械的在线监测和诊断提供依据。