考虑倒箱的Auto Store仓储拣选系统提箱作业优化

师浩森,陈航慧,王 皓,王晓军,杨春霞

(太原科技大学 交通与物流学院,太原 030024)

Auto Store是一种货到人的拆零拣选系统,该系统将密集仓储系统与AGV进行整合,致力于实现高密度存储与高效率拣选的完美融合,如图1所示。虽然Auto Store的优越性显而易见,但该系统在进行提箱作业时,会涉及料箱的倒箱作业,进而导致仓库作业效率的降低。

图1 顶层移动示意图Fig.1 Schematic diagram of top floor movement

目前,国内对于Auto Store的研究还处于起步阶段,关于Auto Store的学术研究成果较少。简素萍等[1]提出了将存储货架从中间分为上下两部分的建议,达到提高Auto Store的存取作业效率的目的;王金龙等[2]使用随机存储策略,推导出了服务强度与料箱填充率之间的关系表达式。王晓军等[3]提出了基于改进A*算法的路径规划和基于贪心算法的区域避碰决策,该方法能有效缩短整体作业完成时间。M.B.M.deKoster等[4]发现专用存储策略效率更高,但储位成本也随之增高,易出现储位浪费的情况。综合Auto Store的国内外的研究现状来看,目前已发表的论文中都未考虑Auto Store中提箱作业的优化问题,因此对该问题的研究存在很大空间,但同时也意味着没有文献可供参考。因Auto Store的提箱作业问题与集装箱的提箱作业比较类似,因此在建模方面,本文将主要参考集装箱的倒箱作业及箱位指派相关的文献。

在集装箱倒箱作业方面,刘志雄等[5]建立了一个多贝位下以堆场贝位和船舶贝位翻箱次数之和最小的优化模型。郭文文等[6]建立了一个单贝位下以最短场桥总作业时间的数学模型。在集装箱箱位指派方面,郑红星等[7]建立了一个箱区间作业量均衡的多目标整数规划模型。高鹏等[8]建立了一个两层嵌套的组合优化模型,分别针对提箱订单和倒箱作业成本最小的移动路径实现倒箱优化。综合集装箱倒箱[9-11]和箱位指派[12]的研究现状,可以看出其主流方向是通过减少倒箱次数来降低倒箱作业的影响,对于Auto Store的倒箱作业来说,不能通过减少倒箱次数来优化倒箱作业,但可以通过优化倒箱作业流程来减少倒箱作业时间。

本文主要研究在考虑倒箱路径的情况下Auto Store的拣选提箱作业的作业效率,提出一种专门适用于Auto Store的倒箱策略,达到通过优化倒箱作业流程来减少拣选提箱作业的作业时间的目的,最后通过与理论倒箱策略下界的比较分析来验证该策略的有效性。

1 问题描述

在提箱作业中,需要被取出的货物所在的料箱称为待提箱。由于Auto Store中料箱的堆存状态和拣选车的作业能力限制,为取出待提箱,常常需要将其上方的料箱移走,这类料箱称为待倒箱,待倒箱移动的目标位置称为待倒箱的落箱位,而移动待倒箱的作业流程称为倒箱作业。以下依次对Auto Store系统,倒箱作业规则以及提箱作业过程进行描述。

1.1 Auto Store系统

Auto Store系统在布局上由若干个存储柱构成,每个存储柱由若干个货格组成,每个料箱所在的位置均由X,Y,Z三维坐标构成,料箱本身具有编号编码,货物的位置由货物所在料箱的编号和其所在位置的三维坐标对应确认,且一个料箱只存放一类货物,因此Auto Store系统的堆放状态时常处于变化中,需要对其堆存状态进行实时监测。

设整个Auto Store系统的堆存状态集合为S,S中任意一个货格si的位置坐标由一个三元组表示,记为si=(Xsi,Ysi,Zsi),因此Auto Store系统的堆存状态S可以表示为:

(1)

式中:Xmax,Ymax,Zmax是该Auto Store系统中行、列、层的最大值。作业期间Auto Store系统的堆存状态S是实时监测的,即是已知的。

1.2 倒箱作业规则

在提箱作业中倒箱时,需要遵循以下几个规则。

规则1:落箱位需在可存储范围内选择。

因存在货格已满或工作台设置等其他因素导致不能进行倒箱作业的情况,所以需设定可存储范围来限制落箱位的选择。vijk表示待提箱gi上第j个待倒箱的第k个落箱位的落箱位置,记vijk=(Xvijk,Yvijk,Zvijk).定义所有待倒箱的落箱位对应的平面坐标集合为W,记W={wi}.则:

(Xvijk,Yvijk)∈W

(2)

规则2:待倒箱的落箱位必须为空,且当落箱位不在第一层时,其下方相邻箱位不为空。

则当落箱位在第一层时,

θ((Xvijk,Yvijk,Zvijk))=0,Zvijk=1

(3)

当落箱位不在第一层时,

θ((Xvijk,Yvijk,Zvijk))=0,

θ((Xvijk,Yvijk,Zvijk-1))=1,Zvijk≥2

(4)

规则3:最大堆存高度限制。

倒箱作业过程中,待倒箱的落箱位所在的存储柱堆积高度需小于最大可堆存高度。

Zvijk≤Zmax

(5)

1.3 提箱作业过程

在提箱作业过程中,需首先确定待提箱集合G,其次对于某个待提箱确定其待倒箱集合U,对于某个待倒箱确定其落箱位集合V,所有待倒箱的落箱位对应的平面坐标集合,最后依次确定所有待倒箱的最短倒箱作业时间,进而确定最短提箱作业时间。

本文只考虑单个订单内的提箱作业,一个订单中包含多种商品,且提箱顺序根据订单顺序确定。

设某一订单内,存在a种商品,定义所有待提箱为集合G.

G={g1,g2,g3,…,gi,…,ga},i=1,2,…a

(6)

式中:a表示该订单内的商品个数,gi表示提箱作业过程中待提箱的初始位置,记gi=(Xgi,Ygi,Zgi).

对于待提箱gi上,存在bi个待倒箱,定义所有待倒箱为集合U.

U={ui1,ui2,ui3,…,uij,…,uibi},j=1,2,…bi

(7)

式中:bi表示待提箱gi上的待倒箱的个数,uij表示待提箱gi上第j个待倒箱在堆场中的初始位置,记uij=(Xuij,Yuij,Zuij).

对于待倒箱uij,存在cij个可放置的落箱位,定义所有落箱位为集合V.

V={vij1,vij2,…,vijk,…,vijcij},k=1,2,…cij

(8)

式中:cij表示待倒箱uij的可选择的落箱位个数,vijk表示待提箱gi上第j个待倒箱的第k个落箱位的位置,记vijk=(Xvijk,Yvijk,Zvijk).

将整个Auto Store系统分为四个集合,用以确定倒箱作业的作业范围以及可作业坐标,分别是以待提箱gi为中心向外水平扩展w距离的平面坐标集合wi0,α,β为偏离待提箱坐标的行列数。

(9)

w中待提箱gi,设以下平面坐标集合:货格已满不能进行倒箱的集合wi1;因工作台设置等其他因素导致不能倒箱的集合wi2;可选择的落箱位的集合wi.

则所有待倒箱的可选择落箱位对应的平面坐标集合W为:

W={wi|wi=wi0-wi1-wi2}

(10)

2 拣选作业数学模型

2.1 模型假设

1)只考虑取货环节;

2)只考虑一个拣选车;

3)拣选车移动速度为匀速,即不考虑重量影响;

4)只考虑单个订单内的取货;

5)设仓库底层左上方的货格为原点坐标(1,1,1);

6)仓库堆存状态和货物位置已知。

2.2 模型符号与决策变量

2.2.1 符号定义

tl——拣选车水平方向移动单位距离所用时间;

td——拣选车垂直方向移动单位距离所用时间;

tc——拣选车水平方向每次转向所用时间;

tbi——待提箱gi上存在bi个待倒箱时的提箱作业时间;

o=(Xo,Yo)——拣选车o所在初始位置;

e=(Xe,Ye)——Auto Store系统的出口所在位置;

(pijk,qijk)——将待倒箱uij搬运到其可选择的落箱位vijk所行走的水平和垂直距离;

Dij——将待倒箱uij搬运到其可选择的落箱位vijk所行走的水平与垂直距离的集合;

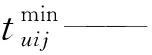
tuij——将待倒箱uij搬运到其可选择的落箱位vijk的倒箱作业时间。

2.2.2 决策变量

2.3 模型建立

根据待提箱位于Auto Store系统的位置,可分为两种情况,分别是待倒箱个数为0和待倒箱个数为j(j=1,2…,bi),计算提箱作业的时间。

当待提箱gi存在0个待倒箱时,提箱作业时间为:

t0=(|Xgi-Xo|+|Ygi-Yo|)·tl+

2(Zmax-Zgi+1)·td+

|Xgi-Xe|+|Ygi-Ye|)·tl+2Zmax

(11)

当待提箱gi上存在bi个待倒箱时,提箱作业时间为:

tbi=(|Xgi-Xo|+|Ygi-Yo|)·tl+

2(Zmax-Zgi+1)·td+(|Xgi-Xe|+|Ygi-Ye|)·

tl+2Zmax

(12)

综上所述,本文建立以单订单内最短提箱作业时间为目标的数学模型:

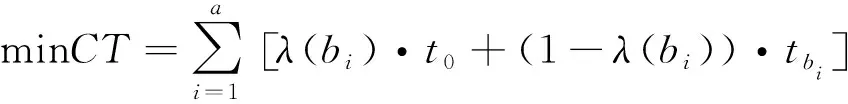
(13)

待倒箱落箱位选择的范围约束为:

(14)

W={wi|wi=wi0-wi1-wi2}

(15)

(Xvijk,Yvijk)∈W

(16)

待倒箱的落箱位选择的时间约束

Dij=

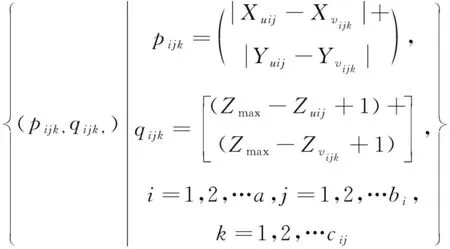
(17)

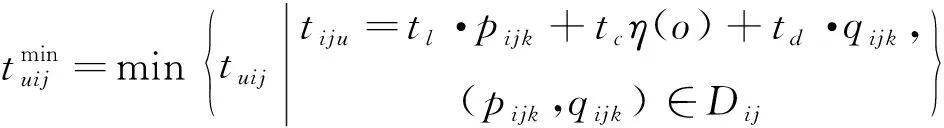
(18)

待倒箱落箱位不能悬空放置的约束为:

(ⅰ)当落箱位在第一层时:

θ((Xvijk,Yvijk,Zvijk))=0

(19)

Zvijk=1

(20)

(ⅱ)当落箱位不在第一层时:

θ((Xvijk,Yvijk,Zvijk))=0

(21)

((Xvijk,Yvijk,Zvijk-1))=1

(22)

Zvijk≥2

(23)

每个存储柱的存储高度要小于最高可堆存高度的约束为:

Zvijk≤Zmax

(24)

每个箱位至多被1个存储箱占用的约束为:

θ(si)≤1,si∈S

(25)

决策变量均为0-1变量,即

θ(si)∈{0,1}

(26)

η(o)∈{0,1}

(27)

λ(bi)∈{0,1}

(28)

3 启发式算法设计

3.1 算法原理

本数学模型可以看做是一个外层模型与一个内层模型嵌套的双层模型,在求解过程中,将内层模型的运行结果作为外层模型的已知条件进行运算。内层模型用来求解每个待倒箱uij的最优落箱位vijk的三维坐标;外层模型将内层模型的计算结果作为已知条件,求出订单内每个商品的最短提箱作业时间,最后求出单个订单内所有商品的最短总提箱作业时间[13]。

3.2 算法步骤

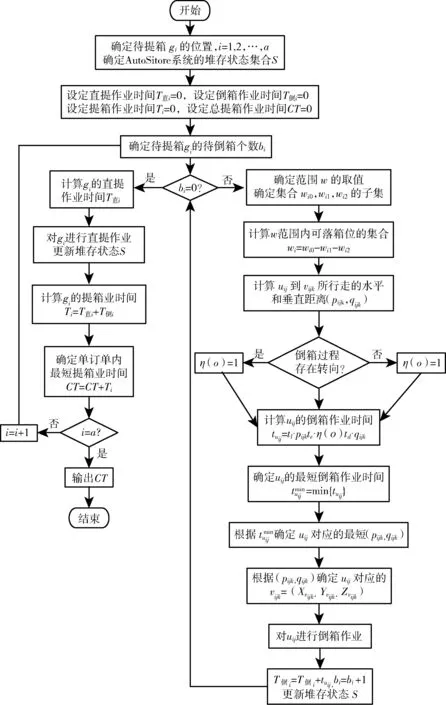
4 算例分析与比较

4.1 算例求解

基于上述算法,以10个商品的单订单为例,Auto Store系统的仓库模型的形状为方形,大小为20*20*8,使用随机数作为Auto Store系统的仓库的存储情况,根据王金龙所得到的Auto Store系统的料箱填充率和服务强度之间的关系,通过Excel生成4至8的随机数,其料箱填充率约为74%,其中w=3;o=(1,1);tl=1;td=1;tc=2.

表1为单订单内商品在Auto Store系统的仓库模型的所在三维坐标,其所在行列层均为随机生成,根据其现存料箱数,可得到每个商品的需倒箱次数,通过算法设计,排除了二次倒箱的影响。

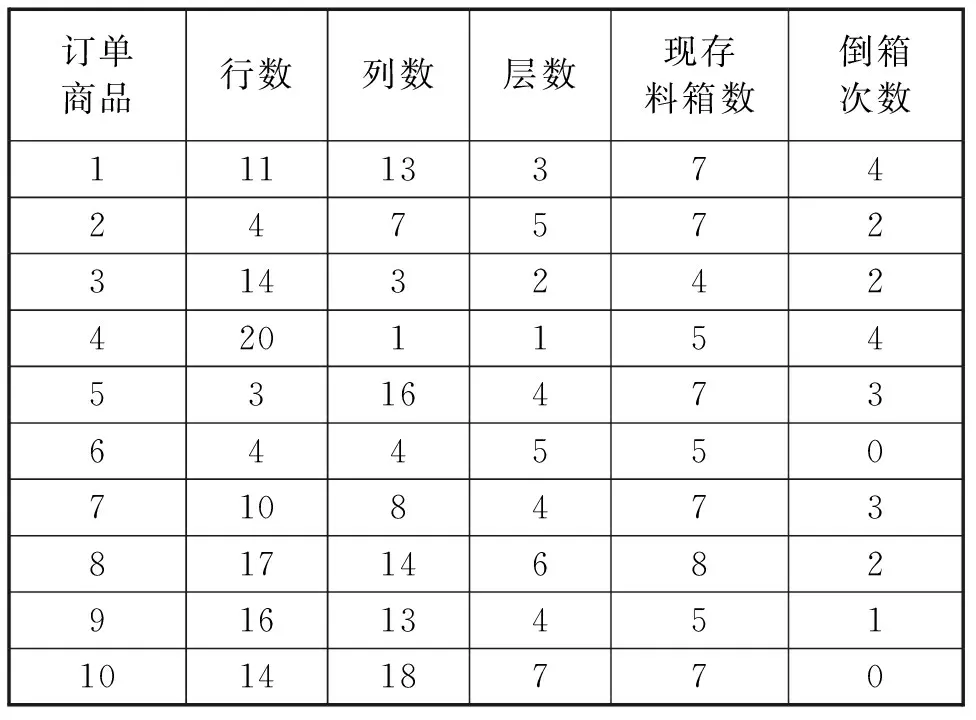
表1 单订单内商品在Auto Store系统中的坐标Tab.1 Coordinates of goods in single order in auto store system

表2为每个商品的倒箱作业时间以及直提作业时间,可以看出该订单内的10个商品的总倒箱作业时间为286,总直提作业时间为566,即完成该订单的总时间为852.

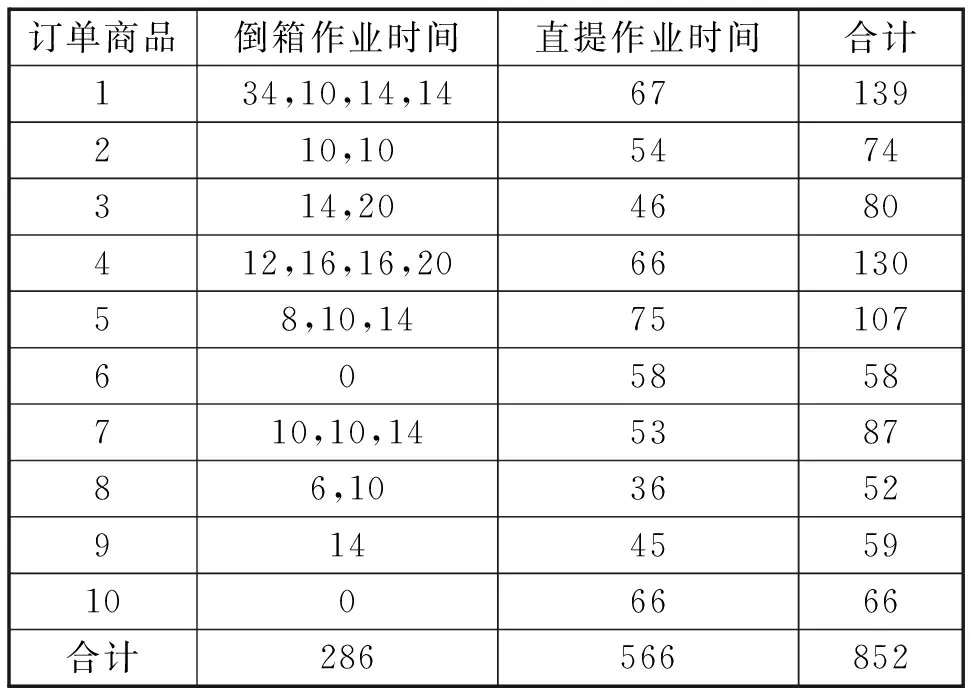
表2 启发算法下的倒箱及直提时间Tab.2 Time of dumping and lifting based on heuristic algorithm

4.2 下界分析

为了验证所提出的模型有效性,计算理论上的下界是必不可少的,通过分析,可知不同的倒箱作业规则会则对倒箱作业时间影响较大。因此,为缩短倒箱作业时间,必须优化倒箱作业流程,提高倒箱作业的效率。因此,本文计算了通过就近原则进行倒箱作业的倒箱作业时间,以此为下界,验证算例的有效性,结果如表3所示。

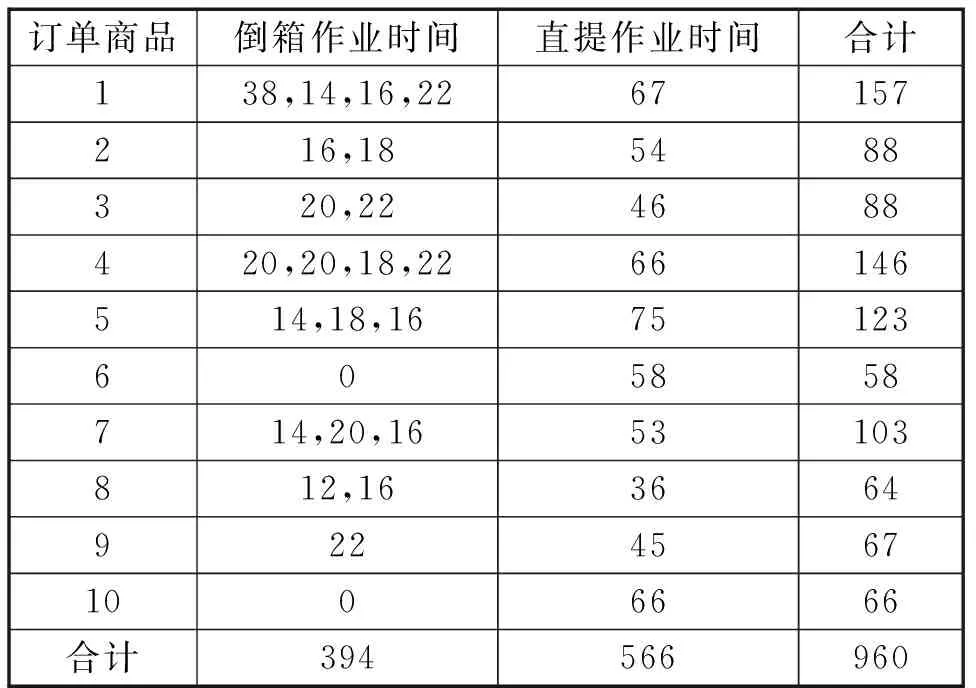
表3 理论下界的倒箱及直提时间Tab.3 The time of dumping and lifting in theory lower bound

具体的下界约束及求解过程如下所示:

(1)确定订单商品的位置。首先按照订单顺序,确定订单商品的有关信息。

(2)进行倒箱作业。倒箱规则如下:待倒箱的落箱位选择范围为w=3,落箱位优先选择所存料箱最少的存储柱内,以保持整个仓库的存储均衡;同时为了减少不必要的倒箱作业时间,本文只考虑与X,Y方向平行的存储柱,避免因转弯导致倒箱时间增加的情况。

(3)进行出库作业。

(4)计算提箱作业时间。将倒箱作业时间与直提作业时间求和便得到提箱作业时间。

4.3 算法比较

利用Excel软件进行计算,为验证算法的有效性,本文通过随机生成的Auto Store系统的仓库模型以及订单信息,采用启发式算法求解,将优化模型与理论下界进行比较分析,结果如表4所示。

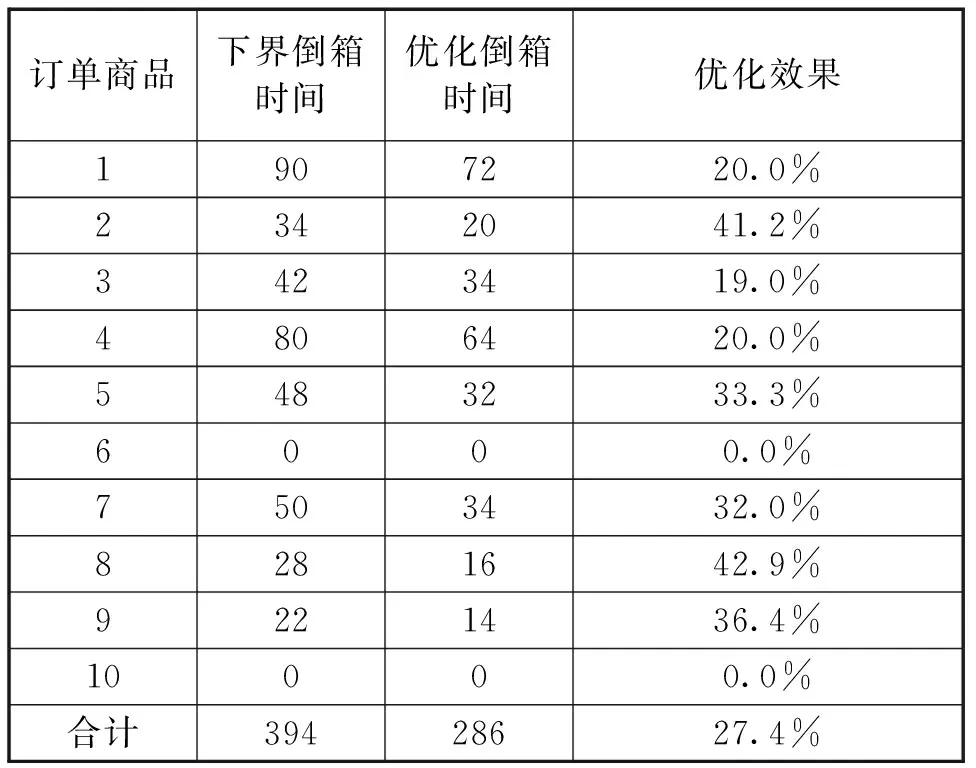
表4 启发式算法和下界比较Tab.4 Heuristic algorithm and lower bound comparison

可以看出,启发式算法下的倒箱作业时间比理论下界有所降低,单订单内的总优化效果约为27.4%,平均每个商品的优化效果达到了约30.6%,这主要是由于倒箱作业规则的不同导致不同倒箱量的产生,表明倒箱作业规则对取箱作业效率影响较大。因此,需要通过对倒箱作业规则的优化以达到提高取箱作业效率的目的。

5 结论

Auto Store仓储系统的提箱作业优化的重要目标之一是提高其提箱作业效率。本文在已知Auto Store仓储系统的料箱存储状态及订单商品的前提下,研究Auto Store仓储系统的提箱作业优化问题,以作业时间来衡量作业效率的高低,建立了以最短提箱作业时间为目标的数学模型,设计启发式算法对模型进行求解,分析了Auto Store仓储系统的倒箱作业下界,并通过算例实验对该问题进行讨论。算例结果表示,Auto Store仓储系统在该启发式算法下的倒箱作业时间与理论下界相比,减少了约27.4%,较好的验证了算法和模型的有效性,为Auto Store仓储系统的倒箱作业优化提供了理论依据。