基于Copula函数的黄海波高周期联合统计分析

张 琦,梁丙臣,邵珠晓

(中国海洋大学工程学院,山东 青岛 266100)

波浪是影响海洋结构物和海上运输的重要海洋环境动力因素之一[1-2],波浪的穿透性和能量强弱与其波高和周期要素的大小息息相关,波浪的波高和周期越大对工程的破坏越强[3-4]。刘文通[5]通过模拟试验和理论计算得出,对于沿岸建筑物和海上孤立式建筑物,波高和周期具有同等重要性,只是表现形式不同。近年来,海洋平台损坏事故频发[6],原因之一是固有振动周期长,容易与长波共振,导致整体响应过大,从而影响结构强度[7]。因此,建立合理预测波浪波高和周期设计参数的统计模型,对于海上工程建筑物安全稳定运行是十分关键的。

传统的波高周期联合概率密度计算要求波高与周期的单变量分布属于同一类型,但实际上波高和周期拟合出的单变量分布往往不属于同一类型,因此根据传统联合分布模型得到的设计值与实际值存在较大误差。Copula函数可以灵活地将不同类型的单变量分布联结在一起,同时还将随机变量之间的相关性考虑在内,目前该函数被广泛用于海洋工程各设计参数间联合分布的研究。Wist等[8]利用二维Gaussian Copula函数建立了波高周期联合分布,并将其应用于日本海域的海洋工程。秦振江等[9]建立了最大有效波高和最大风速的联合分布,结果表明Copula函数可以较好地模拟实际数据。陈超等[10]采用Gumbel-Hougaard Copula函数和Clayton Copula函数构造年极值波高与相应风速的联合分布,并与混合耿布尔分布以及耿布尔逻辑分布进行了对比分析,发现Copula函数联合分布可以更好地表现单变量的非正态性。陈子燊等[11]研究了粤东汕尾海区的最大波高和平均周期,择优选取Gumbel-Hougaard Copula函数建立二维联合分布,提出同现重现期和联合重现期的设计值可作为设计波高和相应周期的上下限。宋春艳等[12]利用Gumbel-Hougaard Copula函数构建波高周期联合分布函数,研究表明Copula函数可较好拟合波高周期联合分布。

黄海是太平洋西部最大的边缘海,针对该海域的波浪周期联合分布研究较少,且以往的研究多采用年极值波高及其对应的周期进行联合分布研究,但年极值波高并不一定对应年极值周期。本文基于中国黄海中部海域后报波浪数据,对该海域3个位置点的年极值波高和年极值周期进行统计分析,以期为黄海海域海上平台建设提供参考。

1 研究方法

1.1 数据来源

近岸波浪模拟软件SWAN是基于第三代海浪模型开发的软件,可用于任何尺度下风生表面重力波的计算[13],适用于沿海和近海区域的波浪预报[14]。Shao等[15]利用近岸波浪模拟数值模型SWAN(simulating waves nearshore)对1979—2018年中国近海的波浪场进行了数值模拟,并将模拟的后报数据与浮标实测数据进行了对比分析,模拟结果与实测波浪数据吻合较好。本文以图1所示的黄海海域3个位置点(1号 位置点位于123°E、35°N,2号 位置点位于 124°E、36°N,3号 位置点位于 125°E、35°N)1999—2018年海浪的后报数据作为数据来源,所选用的参数为每小时记录1次的有效波高和谱峰周期,对3个位置点的年极值波高和年极值周期进行统计分析。代表位置点的选取依据为位置点之间距离较远且分散于黄海海域,位置点之间可以构成一个平面以体现区域性和空间性。

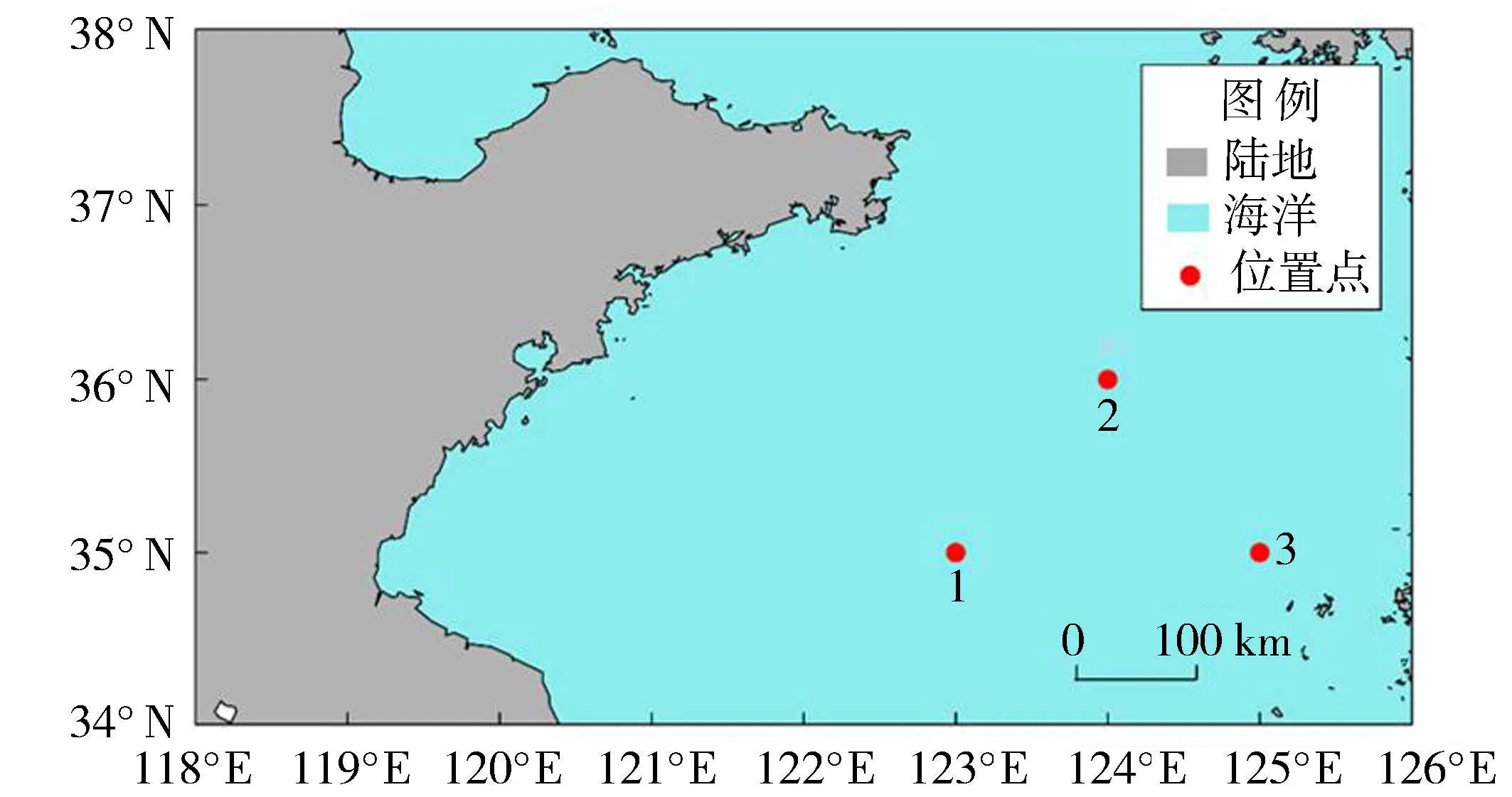
图1 黄海海域3个位置点示意图

1.2 理论分布

对波高和周期年极值数据,本文采用常见的单变量分布进行拟合,包括广义极值(generalized extreme value,GEV)分布、对数正态分布、含有尺度参数和位置参数的t分布、威布尔(Weibull)分布、伽马(Gamma)分布及皮尔逊Ⅲ型(P-Ⅲ)分布。

常用的二维Copula函数类型有Gaussian Copula函数、tCopula函数、Clayton Copula函数、Gumbel Copula函数、Frank Copula函数,其中Gaussian Copula函数和tCopula函数属于椭圆Copula函数,Clayton Copula函数、Gumbel Copula函数和Frank Copula函数属于阿基米德Copula函数。

1.3 拟合优度评价

为了评价不同概率分布模型的拟合效果,采用Kolmogorov-Smirnov(K-S)检验、赤池信息准则(akaike information criterion,AIC)、贝叶斯信息准则(Bayesian information criterion,BIC)和均方根误差(root mean square error,RMSE)来评价模型的拟合优度,并据此选择最优概率分布。

2 结果与分析

2.1 单变量分布

提取1999—2018年的年极值波高和年极值周期分别建立波高和周期的单变量分布,分别采用广义极值分布、对数正态分布、t分布、威布尔分布、伽马分布及P-Ⅲ分布对年极值波高和年极值周期序列进行概率拟合,波高单变量分布和周期单变量分布的拟合参数及拟合优度评价结果分别见表1和表2。

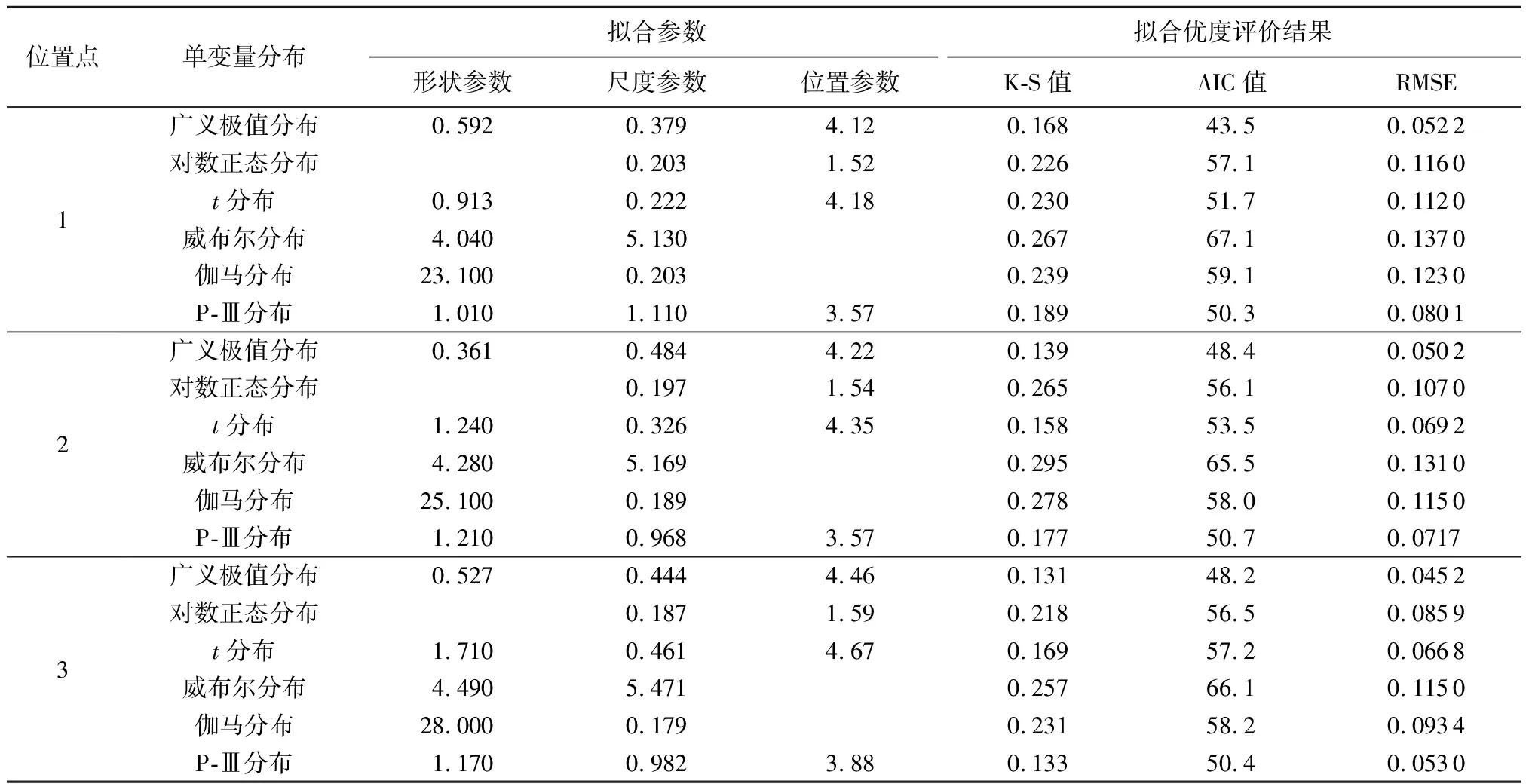
表1 波高单变量分布拟合参数及拟合优度评价结果

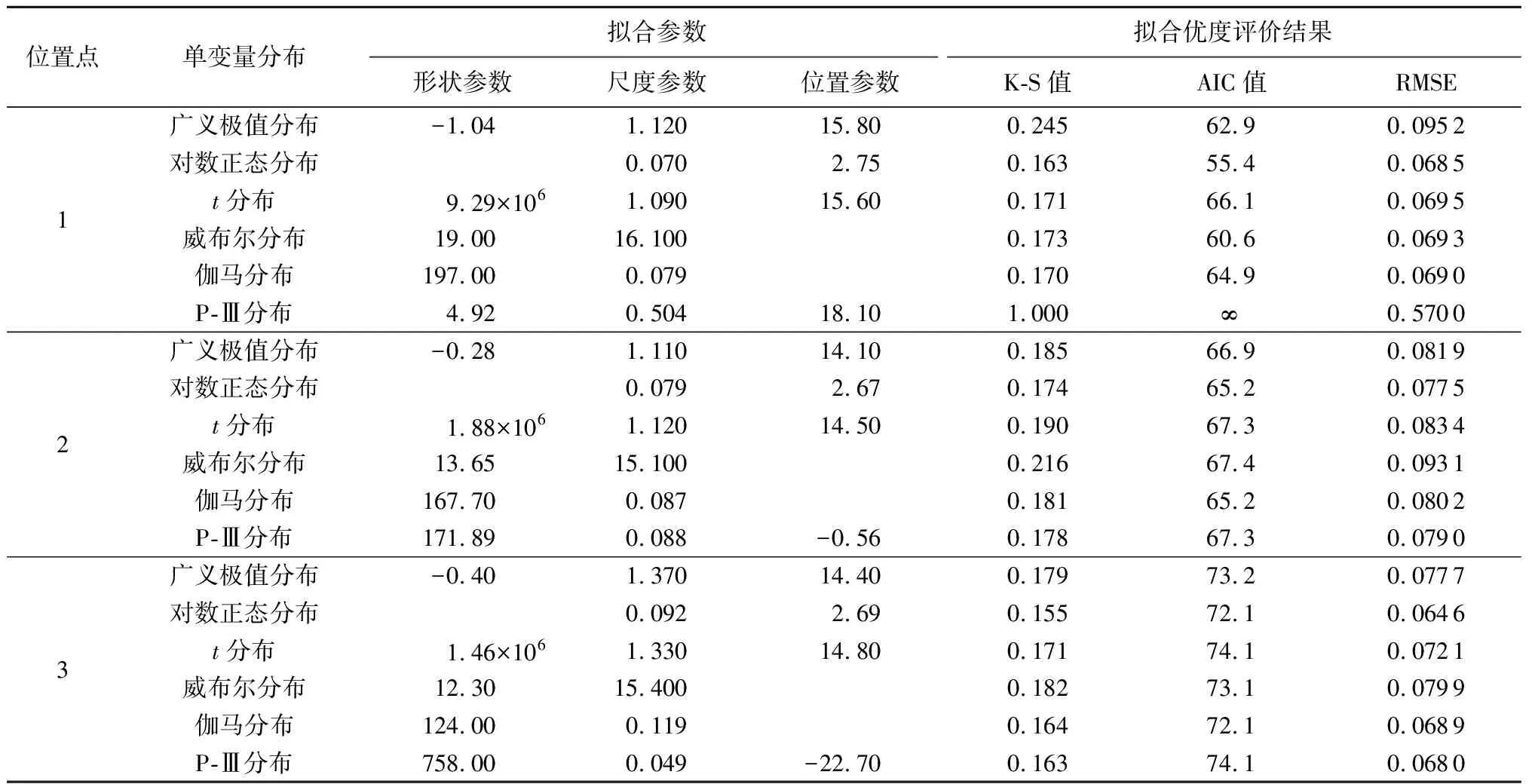
表2 周期单变量分布拟合参数及拟合优度评价结果

对比K-S值、AIC值和RMSE可知,3个位置点的波高最优单变量分布均为广义极值分布,周期最优单变量分布均为对数正态分布。

2.2 联合分布

对于海洋环境要素,其特征变量波高和周期之间存在一定的相关性。经计算,位置点1、2、3年极值波高和年极值周期的Spearman秩相关系数ρs分别为0.0716、0.1306和0.1122,可以看出年极值波高和年极值周期之间存在弱的正相关性。

采用二维正态联合分布对3个位置点的年极值波高和年极值周期建立传统二维联合分布模型,其概率密度函数为

(1)

式中:μ1、μ2为位置参数;σ1、σ2为尺度参数;x、y分别对应两种不同的变量值。

计算得到3个位置点年极值波高与年极值周期二维正态联合分布累积概率与经验分布累积概率散点图如图2所示。

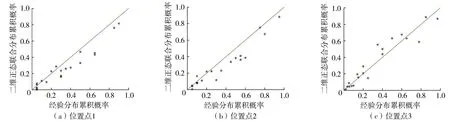
图2 二维正态联合分布累积概率与经验分布累积概率散点图

分别采用Gaussian Copula函数、tCopula函数、Clayton Copula函数、Gumbel Copula函数和Frank Copula函数进行拟合,采用极大似然估计法进行参数估计并计算拟合优度评价指标,二维Copula函数拟合优度评价结果见表3,3个位置点年极值波高与年极值周期二维Copula函数联合分布累积概率与经验分布累积概率见图3,3个位置点二维Copula函数联合分布累积概率等值线见图4。

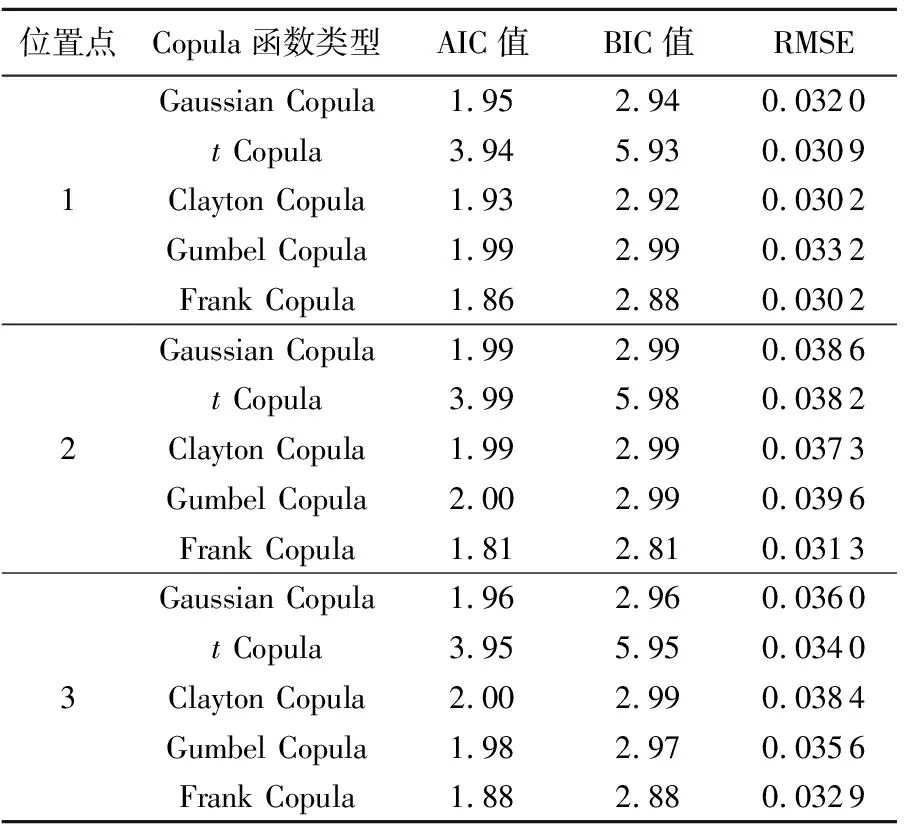
表3 二维Copula函数拟合优度评价结果

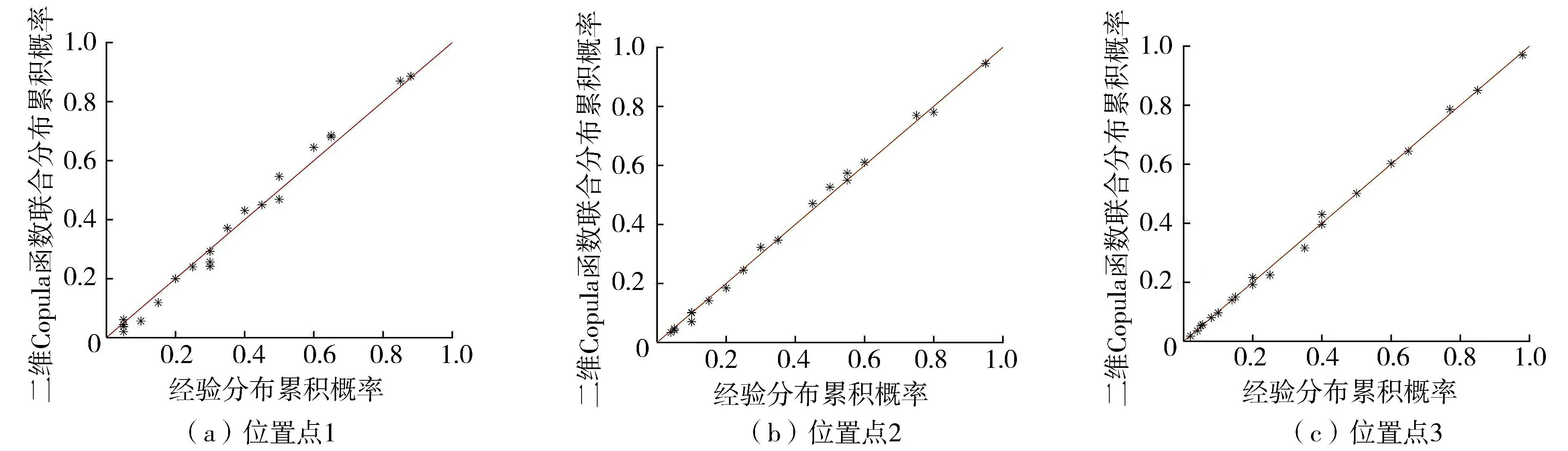
图3 二维Copula函数联合分布累积概率与经验分布累积概率散点图

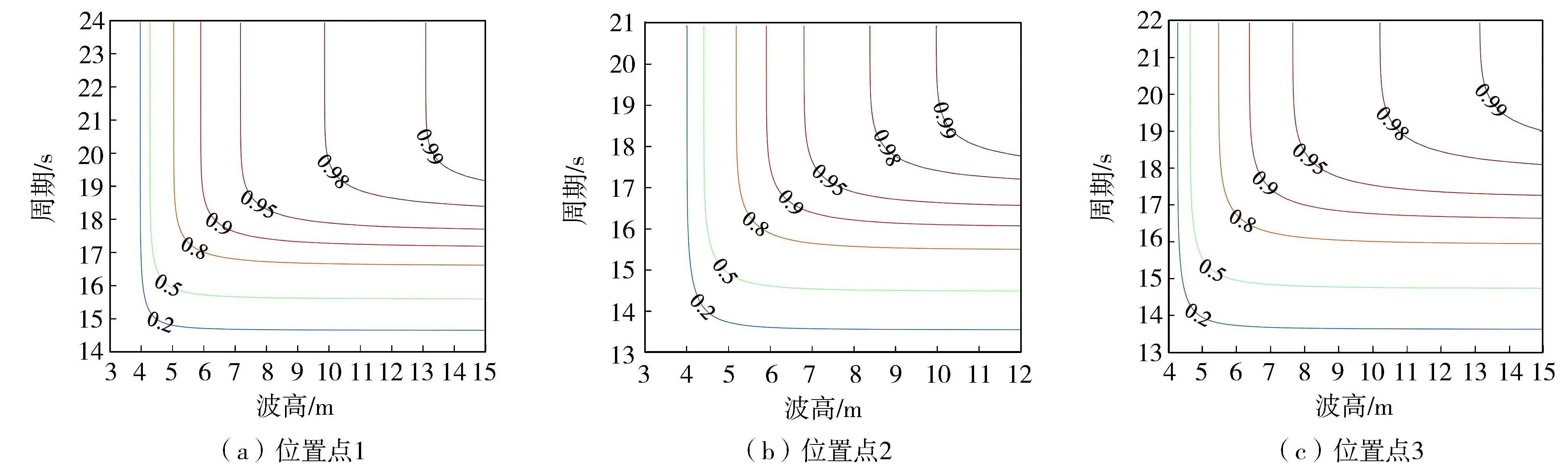
图4 二维Copula函数联合分布累积概率等值线

经计算可以得出,位置点1、2、3的年极值波高和年极值周期最优二维Copula联合函数均为Frank Copula函数,可见Frank Copula函数适用于构建黄海中部海域所选位置点波高周期二维联合分布。对比图2与图3可以看出,相较于传统二维正态联合分布模型,二维Copula函数对于波高周期二维联合分布的拟合效果更好,Copula函数可以不受单变量分布类型和相关关系的限制,更加灵活地构造波高周期二维联合分布。

2.3 重现期计算与分析

重现期计算是对海浪灾害风险进行中长期预测预警的重要参考,在海洋和港口工程应用中是十分重要的[16]。定义单变量重现期为

(2)

式中:T为重现期;F(x)为变量的累积概率;x为变量值。

两变量联合重现期是指变量X1或X2超过某个特定值的重现期,其计算公式为

(3)

式中:T0(x1,x2)为两变量联合重现期;x1,x2分别为两种不同的变量值;P((X1>x1)∪(X2>x2))为任一变量超过某个特定值的联合概率;C(F1(x1),F2(x2))为两变量均未超过某个特定值的联合概率。

由概率论可推导出条件概率为

(4)

式中:P(H≥h|T≥t)为当周期超过某一特定数值时出现超过某一设计波高的概率,可定义为风险概率,其倒数即为条件重现期;h为波高;t为周期;FH(h)为波高超过h的累积概率;FT(t)为周期超过t的累积概率;C(FH(h),FT(t))为联合累积概率。

单变量重现期是根据单变量分布推导出的重现期,但单一要素不足以综合反映海洋灾害的影响,且任一海洋环境要素超过一定数值都会引起海洋极端事件的发生,联合重现期采用的是“或”重现期,即任一变量超过某一特定值的重现期。条件概率可作为工程建筑物损毁风险率,联合重现期可作为海洋工程建筑物波高和周期设计值的最大值,对安全系数要求高的海洋工程建筑物可基于此设计。

分别由最优二维Copula联合函数计算3个位置点年极值波高和年极值周期对应的联合重现期和条件概率,将其与单变量分布设计值进行对比,结果见表4和表5,各位置点不同波高和周期设计频率下单变量重现期、条件重现期及联合重现期计算结果见表6。

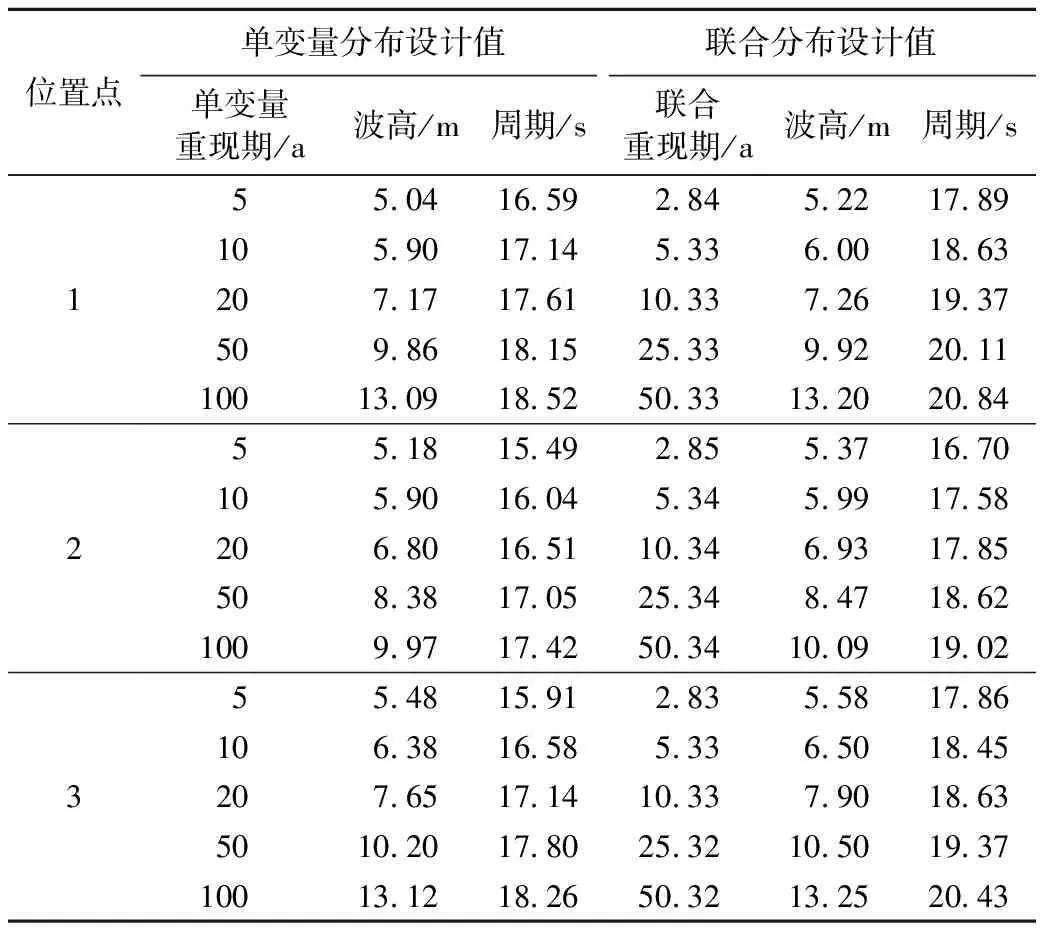
表4 单变量重现期和二维联合重现期

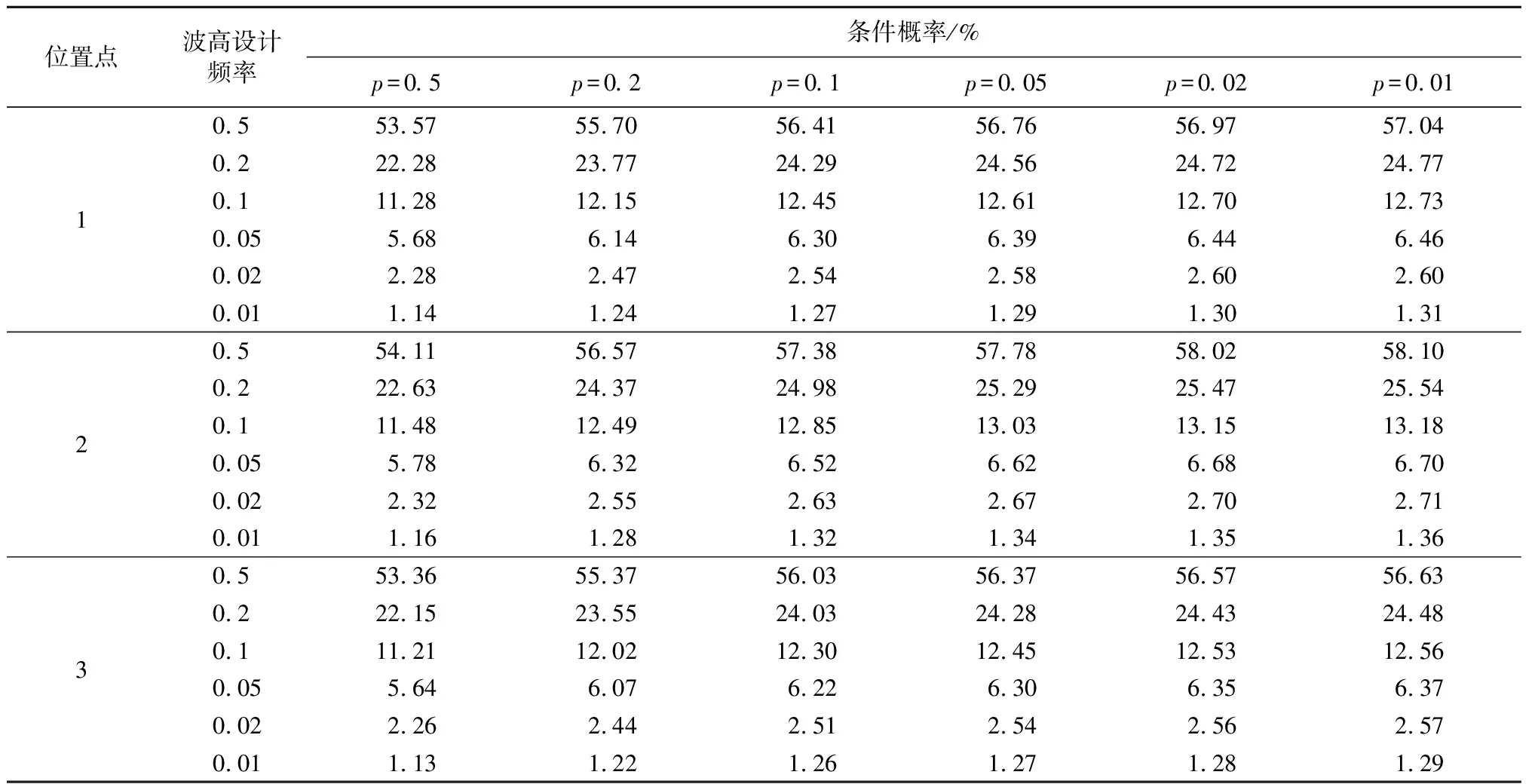
表5 年极值波高和年极值周期条件概率

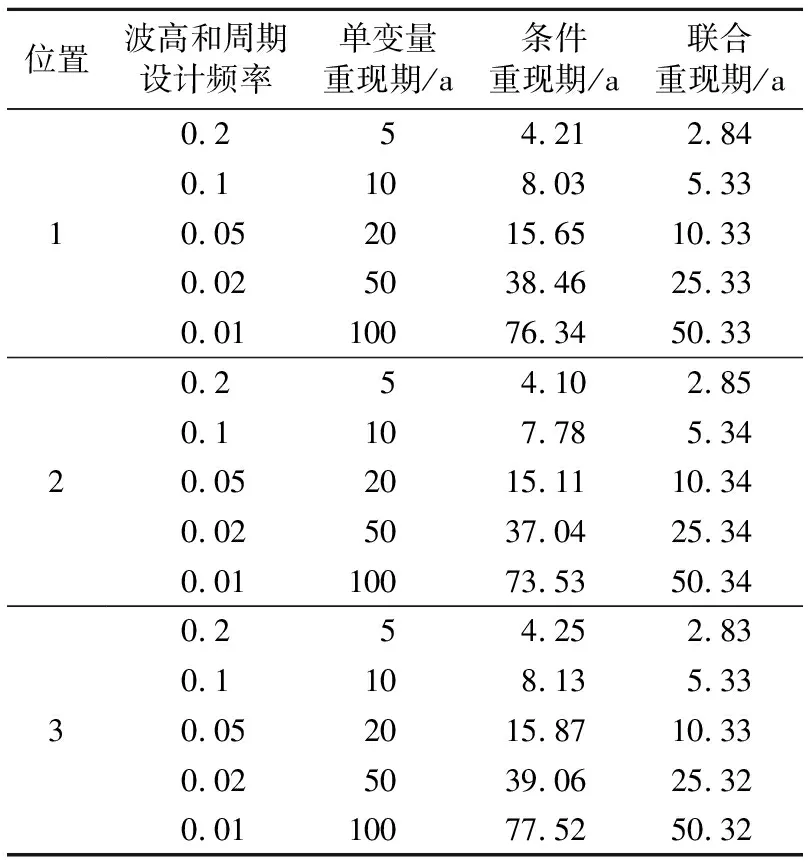
表6 不同波高和周期设计频率下重现期

由表4可知,50a和100a重现期对应的波高,位置点3最大,位置点1次之,位置点2最小;50a和100a重现期对应的波浪周期,位置点1最大,位置点3次之,位置点2最小;联合重现期较单变量重现期小,约是单变量重现期的1/2。按照同频率原理[16],年极值波高和年极值周期联合分布设计值大于单变量分布设计值, 5～100a重现期的设计波高相对差值为0.61%～3.67%, 设计周期相对差值为7.81%～12.53%。

表5显示,在一定周期设计频率条件下,条件概率随波高设计频率的减小而减小:同波高和周期设计频率下年极值波高和年极值周期的条件概率位置点1为1.31%～53.57%,位置点2为1.36%～54.11%,位置点3为1.29%～53.36%。由表5和表6可知,3个位置点波高和周期设计频率0.02的条件概率分别为2.60%、2.70%、2.56%,条件重现期分别为38.46、37.04、39.06a;波高和周期设计频率0.01的条件概率分别为1.31%、1.36%、1.29%,条件重现期分别为76.34、73.53、77.52a。

由表6可知,在相同波高和周期设计频率下,单变量重现期最大,条件重现期次之,联合重现期最小。

3 结 论

a.3个位置点的波高最优拟合分布均为广义极值分布,周期最优拟合分布均为对数正态分布。

b.3个位置点的年极值波高和年极值周期的最优二维Copula联合函数均为Frank Copula函数,黄海中部海域年极值波高周期联合分布特征相似。

c.单变量重现期较两变量联合重现期大,约为联合重现期的2倍。50年一遇和100年一遇对应的波高,位置点3最大,位置点1次之,位置点2最小;50年一遇和100年一遇对应的波浪周期,位置点1最大,位置点3次之,位置点2最小。同波高和周期设计频率条件下年极值波高和年极值周期联合分布设计值高于单变量分布设计值,其中周期设计值的相对差值较波高设计值的相对差值略大。

d.在一定周期设计频率条件下,条件概率随波高设计频率的减小而减小;相同波高和周期设计频率下,单变量重现期最大,条件重现期次之,联合重现期最小。