改进的KNN实时校正方法在山区中小流域的应用

霍文博,高 源,李致家,金双彦,杨明祥

(1.黄河水利委员会水文局,河南 郑州 450004; 2.中国水利水电科学研究院水资源研究所,北京 100038;3.黄河水利委员会山东水文水资源局,山东 济南 250100; 4.河海大学水文水资源学院,江苏 南京 210098)

实时校正是指在实时洪水预报中,根据当前实测信息,结合历史实测与预报信息,对模型的输入数据、结构、参数、状态变量或预报结果进行修正,使其更符合实际,提高预报精度[1-4]。其中,输入数据包括实测降雨量、径流量、蒸散发量,以及部分水文模型所需的气温、空气湿度、风速、潜热通量等观测信息。状态变量是指模型通过输入资料计算出的中间变量,这些中间变量对模型输出结果有直接影响,如降雨径流模拟中模型通过降雨及蒸散发等资料计算得到的土壤含水量。对状态变量校正常用的方法有卡尔曼滤波法[5-7]、集合卡尔曼滤波法[8]等。对预报结果的校正包括对模型计算最终输出的预报流量、水位等进行校正。

常见的水文模型预报结果校正方法有误差自回归(AR)法、BP神经网络法以及K-最近邻(KNN)法等。Ambrus[3]采用基于自回归法的ARMA(auto-regressive and moving average model),实现了对多瑙河水位预报的实时校正。Karlsson等[9]使用KNN法对降雨径流预报结果进行校正,结果表明KNN法比ARMA的校正结果更精确。刘开磊等[10]将KNN法用于洪水预报实时校正中,并与3种常规校正方法(AR法、KF、BPNN)对比,发现KNN法对流量的预报比其他3种常规校正方法更准确,并且KNN法在洪峰附近位置校正结果稳定。阚光远等[11]将KNN法与BP神经网络模型相耦合构建了BK模型,选取3个不同气候类型的流域进行洪水预报研究,结果表明加入KNN算法的BK模型预报精度整体上高于新安江模型。

在山区中小流域,由于流域面积小,汇流时间短,洪水过程陡涨陡落,可供实时校正方法学习预热的资料较少,因此影响了实时校正精度。本文提出了一种基于历史洪水学习的KNN实时校正方法(KNN-H法),以期通过对同一流域历史上发生过的洪水过程进行学习,提高KNN法在山区中小流域的校正精度。

1 KNN-H法的提出

1.1 常用实时校正方法

预报结果校正主要是通过计算每一时刻实测与预报值之间的误差,给出误差时间序列,然后基于该时间序列构建误差预报模型,并估算误差预报模型的参数。以下简要介绍AR法和KNN法2种实时校正方法。

1.1.1 AR法

AR法根据预报值与实测值的误差序列相关关系建立回归方程,通过求解超定回归方程组获得回归方程系数,最终求得预报值的误差估计。AR回归方程为

yt+l=α0+α1yt+α2yt-1+…+αNyt-N+1+et

(1)

式中:y为预报值与实测值的误差;t为时间;l为预见期;N为回归方程阶数;α0、α1、…、αN为回归方程系数;et为余项。

1.1.2 KNN法

KNN法是一种利用概率统计原理进行自主学习的方法[12],其基本原理是选择预报值或预报误差值作为特征向量,根据t时刻的特征向量,在历史样本中选择k个与该特征向量最相似的样本,对相似样本的预报值或误差值反距离加权得到t时刻预报误差估计值[10]。本研究选择模型预报值与实测值的误差作为特征向量,以向量之间欧氏距离最小作为相似性判断标准。KNN法的计算步骤主要包括更新历史样本库、匹配近邻样本、估计预报误差值,校正预报值。

1.2 KNN-H法

在水文预报实时校正中,传统实时校正方法往往选择本场洪水前期的预报误差进行学习预热,然后对未来预报值进行校正。研究[13-16]发现,在山区中小流域洪水预报中,传统实时校正方法在应用中存在以下问题:①由于山区中小流域汇流时间短,洪水过程陡涨陡落,涨洪前可供学习的资料样本数较少,造成实时校正精度不高;②当实时校正预见期较长时,校正后的洪峰往往比实际洪峰滞后出现,造成较大的峰现时间误差。

为解决上述2个问题,本文提出KNN-H法,该方法选择同一流域历史上发生过的洪水过程作为学习样本,通过对历史相似洪水的学习,提高对未来预报值的校正精度。

KNN-H法的理论依据:在同一流域的洪水预报中由于水文模型的结构和参数不变,当历史洪水与当前洪水的降雨过程及前期土壤含水量接近时,同一水文模型对历史洪水的预报误差和对当前洪水的预报误差也会比较接近。如果水文模型对相似的历史洪水预报洪峰偏大或偏小、预报峰现时间提前或延后,那么该模型对当前洪水的预报很有可能也出现同样的偏差。因此通过学习相似历史洪水的预报误差有助于提高KNN法对当前预报值的校正精度。

由于实时校正是对未来时刻的预报值进行校正,在校正时洪水还未出现,并没有实测流量资料,因此无法通过实测洪水过程判断与当前洪水相似的历史洪水。在KNN-H法中,通过降雨资料与前期土壤含水量资料判断相似洪水,认为如果引发当前洪水的降雨过程及前期土壤含水量与历史上某场洪水相似,则当前洪水与该场历史洪水相似。

降雨过程相似有2个方面:①降水量或降雨强度相似,②降雨中心位置相似。在湿润蓄满产流地区,影响产流量大小的主要因素是降水量;而在干旱超渗产流地区,影响产流量大小的主要因素是降雨强度,因此降水量或降雨强度相似是保证洪水过程相似的重要条件。降雨中心位置会影响洪峰出现的时间,当降雨主要集中在流域上游时,径流汇集到流域出口断面所需时间较长;当降雨集中在流域下游时,汇流时间短,洪水起涨快。选择降雨中心位置作为判断相似洪水的标准是为了提高实时校正方法对峰现时间的校正精度。

前期土壤含水量同样是影响产流量大小的重要因素,如果前期土壤含水量差别很大,即使降雨完全相同,产生的洪水过程也会差别很大。前期土壤含水量可以通过日模型率定得到,也可使用遥感或实测资料判断相似性。

KNN-H法通过分析历史洪水的降水量、降雨强度、降雨中心位置和前期土壤含水量,选出与当前洪水相似的一场或几场洪水,通过对相似历史洪水预报误差的学习,判断当前预报值可能存在的误差并对预报值进行校正。具体步骤如下:①在湿润地区选择与当前洪水总雨量和降雨时间接近的历史洪水(设置一个雨量相对误差值作为判断相似的标准,如±20%);在干旱地区选择与当前降雨强度和降雨时间接近的历史洪水。②从第①步选出的洪水中,进一步挑选降雨中心位置接近的历史洪水,降雨中心位置以降雨中心到流域出口断面的汇流路径长度来衡量。③从第②步选出的洪水中,挑选与当前前期土壤含水量接近的历史洪水。④如果历史洪水中没有同时满足上述3个条件的洪水,则选择尽可能多的满足条件的历史洪水作为较相似洪水。⑤将选出的历史洪水实测流量和预报流量资料放入KNN-H法历史样本库中,作为历史资料供KNN-H法学习预热。在KNN-H法中加入一个流量比例系数c=Qs,t/Qs,t-1,其中Qs为模型预报流量。c为当前时刻与前一时刻水文模型预报流量的比值,用来表示预报值所处的洪水阶段,认为连续n个时刻c大于某一值(本研究取1.1)为涨洪阶段,连续n个时刻c小于某一值(本研究取0.9)为退水阶段。由于山区中小流域洪水陡涨陡落,n不宜过大,本研究取n=3。当待校正的预报值处于涨洪或退水阶段时,KNN-H法可以快速定位到历史洪水的相同阶段,对历史洪水该阶段的预报值与实测值误差进行重点学习。

剩余计算步骤与KNN法相同,通过匹配近邻样本,估计预报误差值等最终得到校正后的预报流量值。由于在实时预报过程中降雨也在持续,因此KNN-H法在判断相似历史洪水时使用的降水量资料也是实时更新的,通过当前观测的降雨在历史库中寻找与之降水量或雨强接近的历史洪水,在降雨持续的过程中,KNN-H法每个时段都更新雨量值并重新在历史库中寻找相似洪水,随着降雨持续选择的历史洪水可能会发生变化,当历史洪水变化后选择更新后的历史洪水作为学习样本,并对当前洪水进行校正。

2 KNN-H法验证

2.1 研究流域

选择陕西省位于半干旱地区的2个中小流域——曹坪水文站以上流域和志丹水文站以上流域(图1)为研究流域。曹坪水文站位于黄河无定河水系的二级支流岔巴沟,控制面积为187km2,多年平均降水量为443mm;志丹水文站是黄河北洛河水系周河的控制站,控制面积为774km2,多年平均降水量为509.8mm。两流域均位于陕北黄土高原地区,属于山区中小流域,流域面积较小,洪水过程陡涨陡落,同时两流域雨量站密度相对较高,降水量及径流量资料系列完整。

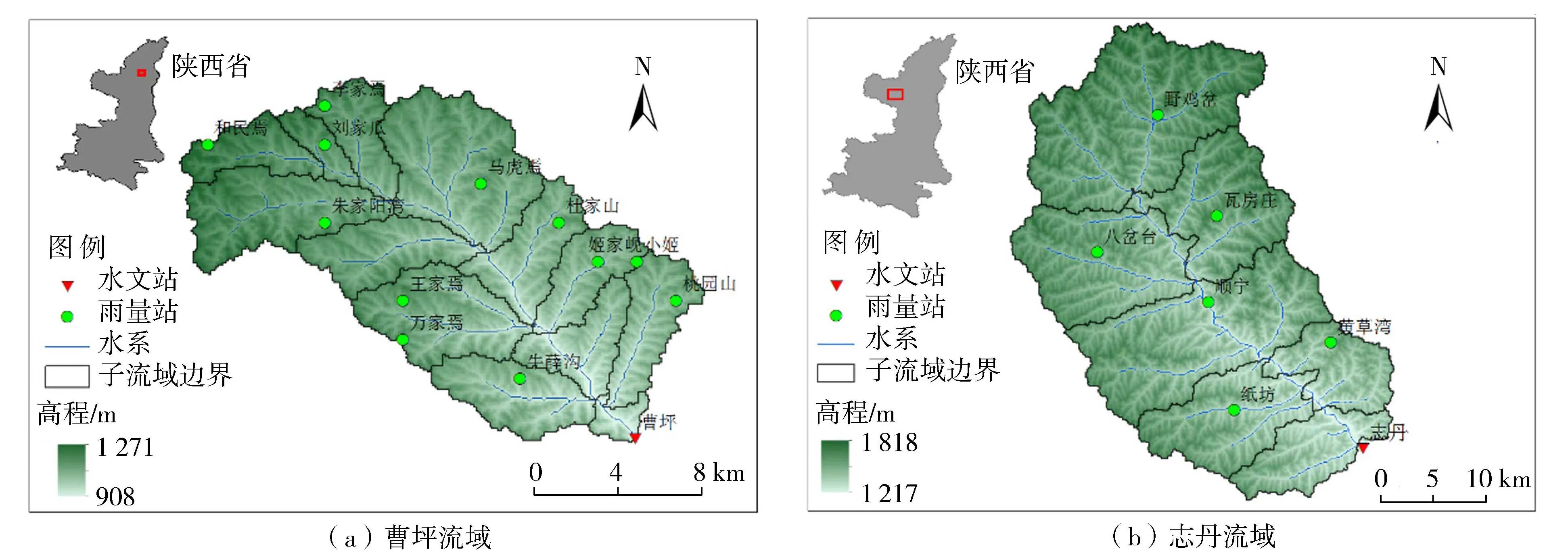
图1 研究流域

2.2 洪水预报模型选择

选择格林-安普特模型、GA-PIC模型[17]和分布式格林-安普特模型[18]3个超渗产流模型在曹坪和志丹流域进行实时洪水预报。3个模型均使用格林-安普特下渗公式计算超渗地面径流,其中格林-安普特模型在计算时将流域划分为若干子流域,在每个子流域上单独计算蒸散发及产汇流过程,并利用一条经验下渗能力分布曲线来反映流域下垫面分布不均的特点;GA-PIC模型是将格林-安普特模型中的经验下渗能力分布曲线改进为具有物理基础的下渗能力分布曲线,可以更准确地反映半干旱地区降雨及下垫面特征的时空变化情况,为半分布式模型;分布式格林-安普特模型基于正交网格计算流域蒸散发及产汇流过程,其中蒸散发计算使用新安江模型中的3层蒸散发模型,坡面汇流采用一维扩散波方程组计算,河道汇流采用基于网格的马斯京根汇流演算法计算,该模型是一种具有物理基础的全分布式超渗产流模型。3个模型所使用的产流计算公式相同,但在流域下垫面划分及异质性计算时采用的方法不同。以上3模型均被证实适用于陕北黄土高原地区洪水预报[17-18]。

2.3 不同实时校正方法结果对比

使用AR法、KNN法和KNN-H法对3个模型预报结果进行校正。由于实时洪水预报预见期基本等于流域平均汇流时间,为了保持实时校正预见期与实时预报预见期相同,选择流域平均汇流时间作为实时校正预见期,其中曹坪流域平均汇流时间为70min,志丹流域平均汇流时间为180min。

在曹坪流域选择2000—2010年共17场洪水,其中前10场洪水用来率定模型参数,后7场洪水用于检验模型预报结果;志丹流域选择2000—2010年共13场洪水,其中前8场洪水用来率定模型参数,后5场洪水用于检验模型预报结果。采用3种实时校正方法分别对各流域验证期洪水预报结果进行校正,KNN-H法选择率定期洪水作为历史洪水资料,从率定期洪水中挑选出与当前校正洪水相似的历史洪水,通过学习历史洪水的预报误差进而校正当前洪水预报值。

选择径流深相对误差(Er)、洪峰相对误差(Ep)和峰现时间误差(Et)3个指标评价模型预报及实时校正精度,各模型预报及校正结果见表1,表中误差值为各场洪水的绝对平均值。

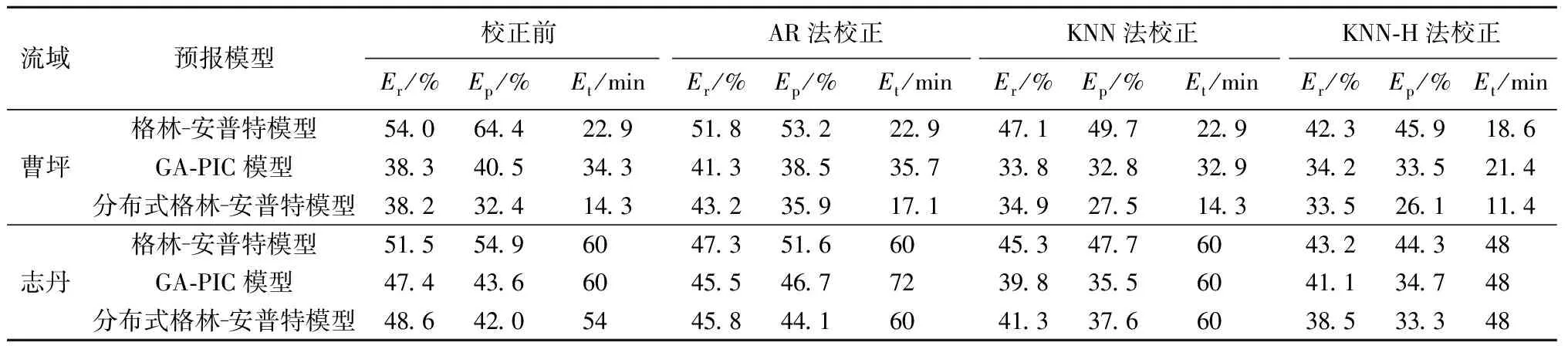
表1 3种实时校正方法应用对比

3个模型在两流域预报的径流深和洪峰相对误差较大(表1)。由于黄河中游黄土高原地区产流模式复杂,以超渗产流为主,同时伴随蓄满产流,该地区洪水预报精度一直较低。本文3个模型经过了充分率定,总体预报结果好于目前平均水平。

由表1可知:①经3种实时校正方法校正后,各模型Er和Ep总体上均较校正前有所降低。以曹坪流域为例,3个水文模型Ep分别为64.4%、40.5%和32.4%,经AR法校正后洪峰相对误差分别为53.2%、38.5%和35.9%;经KNN法校正后洪峰相对误差分别为49.7%、32.8%和27.5%;经KNN-H校正后分别为45.9%、33.5%和26.1%。总体上KNN和KNN-H法校正精度高于AR法。②经AR法和KNN法校正后,各模型预报结果Et并未有效降低,经KNN-H法校正后3个模型Et均较校正前有所降低。以志丹流域为例,3个水文模型Et分别为60、60、54min,经AR法校正后Et分别为60、72、60min,相比校正前略有增大;经KNN法校正后Et均为60min,与校正前相比变化不大;经KNN-H法校正后Et均为48min,均比校正前有所降低。③单独对比KNN法和KNN-H法校正结果可以看出,增加了对历史洪水预报误差学习之后,KNN-H法校正结果在Er、Ep方面较KNN法略有降低,而在Et方面,KNN-H法在两流域的校正结果均较KNN法有明显降低。

图2(a)为KNN-H法在率定期洪水中找到的与当前洪水相似的历史洪水(2001081723号洪水),图2(b)为2种实时校正法对2006082916号洪水预报值的校正结果。在这两场洪水中,GA-PIC模型对总径流深和洪峰流量的预报结果都偏小。2006082916号洪水包含3个洪峰过程,其中第3个洪峰最大,实测洪峰流量154m3/s,GA-PIC模型预报洪峰流量为42.8m3/s,相对误差为-72.2%;经KNN法校正后洪峰流量为172.4m3/s,相对误差11.9%;经KNN-H法校正后洪峰流量为165.7m3/s,相对误差7.6%,稍小于KNN法校正结果。GA-PIC模型预报峰现时间比实测峰现时间晚30min,经KNN法校正后峰现时间比实测峰现时间晚90min,误差较大,因此确定性系数只有-0.05;经KNN-H法校正后峰现时间比实测峰现时间晚20min,优于模型预报结果,校正后确定性系数达到0.69。

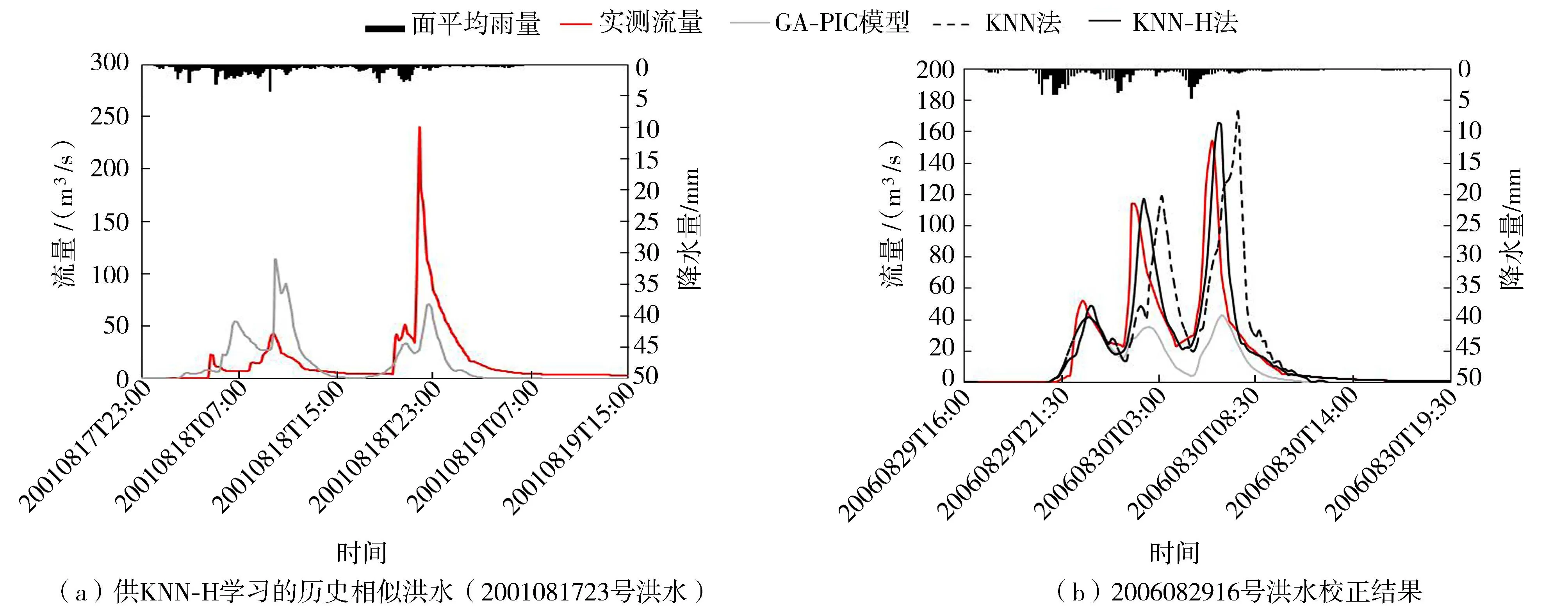
图2 曹坪流域2006082916号洪水KNN法与KNN-H法校正结果对比

由图2(b)可知,在第1个洪峰过程中,KNN法校正结果与GA-PIC模型模拟结果完全一致,这是由于KNN法使用本场洪水前期流量资料进行学习预热,在第1个洪峰出现时,KNN法还未完成预热,因此没有对模型预报结果进行校正。而KNN-H法通过对2001年发生的历史洪水预报误差学习后已经完成预热,因此对2006082916号洪水中第1个洪峰过程做出校正,校正后洪峰流量与实测值更为接近。在第2个和第3个洪峰过程中,KNN-H法校正后洪峰相对误差均较KNN法校正结果有所降低,尤其是峰现时间误差明显降低。以第3个洪峰过程为例,实测洪峰发生在8月30日6:00,GA-PIC模型预报洪峰发生在6:30,峰现时间误差为30min。由于在曹坪流域实时校正预见期设置为70min,在校正6:30模型预报洪峰时参考的是70min之前的资料,也就是5:20之前的预报误差,此时模型预报值较实测值严重偏小,因此KNN法将预报值校正增大。从图2(b)中可以看出,在6:30之后实测洪水进入退水阶段,而KNN法校正结果则继续增加,直到7:30KNN法校正结果出现洪峰,之后开始下降,这是由于6:20时实测流量下降到与模型预报值接近,KNN法认为此时预报值不再严重偏小,因此校正结果开始下降,导致校正后的峰现时间比实际晚了90min。而KNN-H法在对2001年的历史洪水进行学习后,知道模型预报洪峰流量偏小,峰现时间偏晚,因此在校正时提前做出判断,降低了校正结果的洪峰流量误差和峰现时间误差,校正精度比KNN法高。

KNN法通过学习本场洪水前期资料后进行校正会存在一定的滞后性,校正结果比实测洪水过程滞后一段时间,并且校正预见期越长滞后的时间也越长。而KNN-H法通过学习历史洪水资料,当预报值进入到涨洪阶段时,KNN-H法能够快速定位到历史洪水的涨洪阶段,分析历史预报误差后迅速对当前预报值做出校正,因此KNN-H法校正结果的峰现时间误差更小。

3 结 语

本文构建了KNN-H法,以陕北黄土高原地区2个山区半干旱中小流域为研究区域进行验证,并与传统KNN法和AR法进行对比。结果表明,各模型预报结果经3种实时校正方法校正后,径流深相对误差和洪峰相对误差总体上均有所降低,KNN法和KNN-H法校正精度总体高于AR方法。经AR法和KNN法校正后,各模型预报结果峰现时间误差并未有效降低,而KNN-H法校正结果的峰现时间误差较校正前有明显降低。

山区中小流域由于汇流时间短,洪水过程陡涨陡落,KNN法在实时校正中面临预热期资料不足问题,影响校正精度,同时当校正预见期较长时,KNN法校正结果会比实测洪水过程滞后一段时间。KNN-H法通过对历史洪水预报误差进行学习,有效解决了预热期资料不足的问题,当预报值进入到涨洪或退水阶段时,KNN-H法能够快速定位到历史洪水的相同阶段,分析历史预报误差后迅速对当前预报值做出校正,因此KNN-H法校正结果精度高于传统KNN法。