对提高数学解题教学有效性的几点思考

安徽省蒙城县第六中学 (233500) 邵 源

当下,数学解题教学中,不少教师仍然采用“对答案”式的教学.实际上,“标准答案”看起来确实完美无瑕,但它不一定最适合学生的,学生只能感知“应该怎么做”,却不知“为什么这样做”,也不会思考“还能怎么做”,这样不仅不会提高学生分析和解决问题的能力,而且会增加学生的课业负担,与“减负增效”的教学目标背道而驰.就此,本文就解题教学有效性总结归纳了几点教学建议,供参考.

一、构建知识网络,为问题的解决提供思路

高考题重视考查学生综合能力和综合素养,因此一些中高档的命题多在知识网络的交汇处构思设计.要解决此类问题,需要以完善的知识体系为支撑.在解题教学中,教师应从整体的角度出发,关注知识点间的内在联系,引导学生通过知识的迁移和重构来优化已有的认知网络,让学生学会根据已有知识网络分析问题,以此提高学生解题能力.

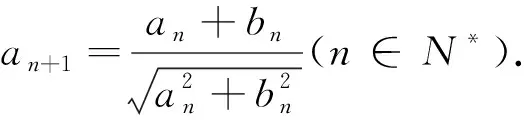
以上从不同角度出发,与函数、不等式、三角函数等相关知识联系在一起,为问题的解决提供了合理的思路.

二、掌握通性通法,为问题的解决提供保障

一般地,高考所考查的是基础知识、基本技能、基本方法,然部分教师为了追求速度,或者展现自己的教学能力,常常强化一些特殊方法,这样学生记住了特殊方法却忽视了通性通法.特殊方法在解决一些问题时确实高效,但是其缺乏一定的通用性,这样过度强调特殊方法很容易将学生代入“死胡同”,影响解题效果.因此,在解题教学中,教师应重视通性通法的掌握,达到会一题通一类的效果,真正提高解决问题的能力.

例2 设a∈R,若x>0时,均有[(a-1)x-1](x2-ax-1)≥0,则a=.

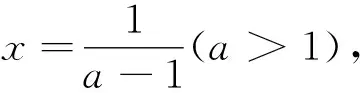
这样,将不等式恒成立问题转化为函数问题,运用数形结合的思想方法顺利地解决了问题.解题教学中,不仅要追求结果,更要追求过程,重视揭示问题的本质,重视强化学生的基础知识、基本技能和基本方法,以此在夯实基础的同时,优化认知,提升能力.

三、重视反思归纳,为问题的解决提供依据

在日常教学中,大多教师都遇到过这样的困惑,有些问题反复讲、重复做,但是学生在解题时依然会犯错.出现这一现象的重要原因之一就是在平时教学中没有进行反思和归纳,学习中出现似懂非懂的情况,从而影响解题效果.为了改变这一局面,教学中教师要预留时间让学生进行总结归纳,争取由掌握一道题变为掌握一类题,以此达到减负增效,融会贯通的效果.

例3 (1)当x>y>e时,求证:xy

其实,学生之所以会出现“懂而不会”、“一错再错”等情况,与教师的“教”息息相关.教学中,部分教师片面地追求速度,使得对数学知识、思想、方法等内容的挖掘不够深入,并未触及问题的本质,这样学生在解题时很容易陷入囫囵之中,影响解题效果.在日常教学中,教师要既要关注思维的深度,也要重视思维的广度,通过设计一题多变、一题多解,多解归一等活动发散学生的数学思维,帮助学生积累数学活动经验,优化学生的已有认知结构,提高学生解题能力.同时,在数学解题教学中,教师要预留时间和空间让学生独立思考、自主探究,引导学生利用已有的知识网络主动分析问题,学会用变化的眼光看待问题,合理应用解题方法解决问题,以此通过多角度、全方位地分析来把握问题的本质,在巩固学生已有知识和已有经验的基础上,提高学生数学能力和数学学力,提升学生数学素养.