对一道圆锥曲线模拟题的探究与发现*

福建师范大学附属福清德旺中学 (350319) 周 宁 倪 娜

1 试题与标答呈现

本题是2023届温州一模数学第21题,主要考查直线与双曲线的位置关系等基础知识,考查推理论证能力和运算求解能力,考查逻辑推理、数学运算和直观想象素养,体现基础性、综合性与创新性．

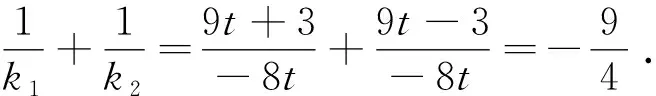
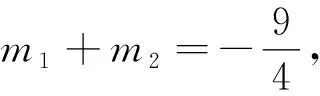
笔者对以上第2问的解析有以下两个疑惑:

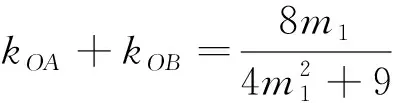
(2)题设已明确直线PF1,PF2斜率分别为k1与k2,为什么参考解析在解决第二问中反而用x型直线形式去解决,是因为运算的效率比较高吗?

2 疑惑与解法剖析

疑惑1的剖析

图1

疑惑2的剖析

用条件中的k1,k2解决第2问可以得到如下解法:

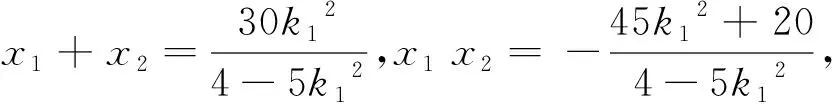
再审视目标式的结构,发现这是经典的斜率结构,因此还可以考虑进行齐次化,转化为关于斜率的一元二次方程进行求解.

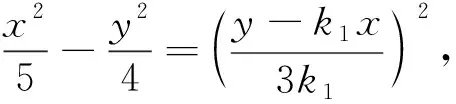
3 溯源及本质赏析

本题是源于2010年山东卷文科数学第22题的改编:

图2

(1)求椭圆的标准方程;(2)设直线PF1,PF2的斜率分别为k1,k2．

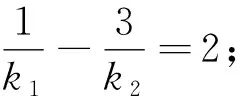
对上述两个试题的第2问进行比较分析,可以发现二者问题背后的本质是一致的:即过椭圆(或双曲线)的一个焦点作两条割线交于四个点,若这四个点与原点的连线的斜率和为0,则这两条割线的斜率和为0或斜率乘积为定值．同时,若过另一个焦点作其中一条割线的平行线,则与另一条割线的交点的轨迹是某条坐标轴且不包含原点(当斜率和为0时)或双曲线(或椭圆)(当斜率乘积为定值时),即有如下的结论:

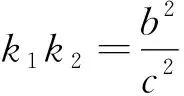
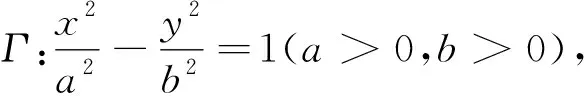
证明类似,留给读者完成．

4 结语

运算能力是解析几何考查的重点内容,但“几何的眼光”才是首要考查的对象．通过分析几何图形的要素及其性质,借助“形”的直观思考“数”的表达,结合图形的几何特征感知数量关系及本质属性,有助于理解问题,寻求问题解决的思路,这才是合理的解决解析几何问题的思维逻辑．