让学生在解题学习中学会概括
王小林

摘 要:微专题教学是中学数学复习阶段一种新的复习课型,得到了很多教师的研究和实践.微专题教学主题聚焦于一类问题或一个基本图形,一题多变、多题归一,有助于学生对一类问题的归类与识别,提升学生思维品质,也有利于“就题论道”.
关键词:微专题教学;三角形内接矩形;问题的归类与识别
数学概括是一种能力,能力只存在于人的特定活动之中,并在活动中形成和发展[1].因此,概括不是静态的,它是在数学学习活动中形成、运用并不断得到发展的思维动作.本文从一道教材经典问题出发,研发一节微专题复习课,在解题教学中积极践行涂荣豹教授关于“要重视培养学生概括能力”的论点.
1 “三角形内接矩形问题”微专题教学设计
教学环节(一) 从教材习题出发
例1 (教材习题)如图1,面积为48的△ABC是一塊锐角三角形余料,边BC=12,要把它加工成正方形零件,使正方形DEFG的一边在BC上,其余两个顶点分别在AB,AC上,求该正方形零件的边长.
教学预设:这道题可安排基础较弱的学生讲解思路,然后请优秀学生进行点评.接着给出“变式1”.
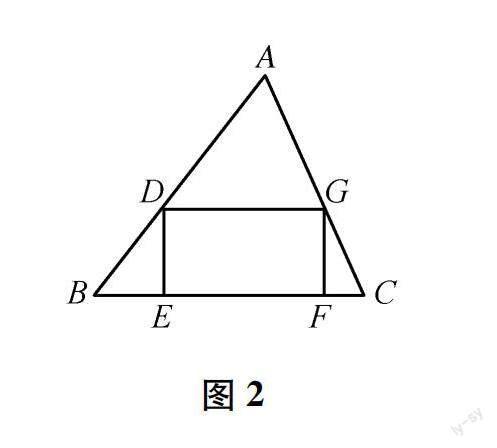
【变式1】如图2,△ABC的面积为48,BC=12,矩形DEFG的四个顶点分别在△ABC的各边上,且DE∶EF=1∶2,求矩形DEFG的面积.
教学预设:从“内接正方形”到“内接矩形”,且给出了矩形相邻两边之比为1∶2.学生可以继续运用相似三角形的对应高之比等于相似比,列出方程求出矩形的相邻两边,从而求出面积.
教学环节(二) 探究三角形内接矩形的面积的最大值
【变式2】如图2,△ABC的面积为48,BC=12,矩形DEFG的四个顶点分别在△ABC的各边上,分析矩形PQMN的面积的最大值.
教学预设:继续运用相似三角形对应高之比等于相似比来分析,可以将矩形相邻两边用同一个未知数x表示出来,进一步得到矩形的面积与x之间存在二次函数关系,于是可借用二次函数的最大值分析方法求解.求解之后,将问题“一般化”,删减“△ABC的面积为48,BC=12”,给出“变式3”.
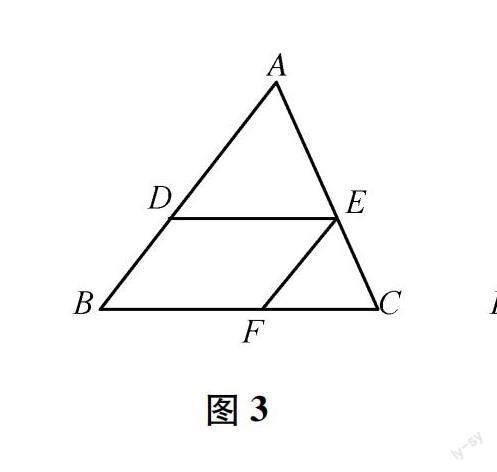
【变式3】如图3,△ABC中,点D,E,F分别在边AB,BC,AC上,且DE∥BC,EF∥AB.分析平行四边形BDEF的面积取得最大时与△ABC的面积的关系.
小结问题1:本课练习中哪几道习题是以前就遇到过的?哪些习题是没有见过的?举例说说.没有见过的习题,你觉得怎样转化为“以前遇到过的习题”?
小结问题2:本课解题与学习中,你对哪道(或哪类)习题留下较为深刻的印象,举例说说.
小结问题3:你能否根据本课学习的某一道习题为原型,改编一道习题与小组同学先交流一下改编意图和解题思路.
布置作业:可安排3道与本课时高度相关的习题,作为巩固训练.限于篇幅,不再给出.
2 教学立意的进一步阐释
2.1 专题复习有助学生对同类问题的归类与辨识
聚焦于某一类问题或某一个基本图形的专题复习有助于学生对这类问题的深刻理解,以便帮助学生学深、悟透.专题复习课与传统的以知识点为复习主题的复习课相比,后者虽然以某个知识点为复习主题,但是所选的习题类型、解题方法、转化策略可能各不相同,学生需要在这些“风格不同”的习题之间反复切换,容易形成解题疲倦,是题海战术的一种
表现,复习效率往往事倍功半.而专题复习课,着眼于一类问题或一个基本图形的多种变式与拓展,学生只需围绕一个问题情境或问题主干深入思考和深度探究,有助于学生今后再遇到类似问题时,能快速识别同类问题、高效解答.
2.2 专题复习有利于学生解题和思维品质的提升
由于专题复习聚焦于某一类问题的深入挖掘,所以对学生解题的思维品质有显著的提升.比如,上面课例中关注的三角形内接矩形问题的深入探究,学生在这样的专题复习训练之后,遇到其它的经典问题、基本图形,就可能学会深入思考、习得方法,促使他们有“做一题、会一类、通一片”的解题追求;从思维品质上来看,主要训练了学生思维的深刻性与灵活性.特别地,让学生在“一题多变”中感悟“多题归一”,不但训练了学生的解题能力,而且向学生传递了“解题学习中的某些规律可以通过归纳式概括获得”[1].
2.3 专题复习的课堂小结要引导学生“就题论道”
专题复习的主要任务是解题研究和变式拓展,但也要十分重视课堂小结的预设,这也是上文课例中特别安排了3个“小结问题”的教学立意.具体来说,专题复习的课堂小结要紧紧围绕本课训练内容展开,避免泛泛而问“这节课学到了什么?这节课感悟了哪些思想方法?”之类.离开学习内容的思想方法的小结是空洞无力的,教师在预设课堂小结时,一定要注意让学生结合前面所学内容进行梳理和回顾.这也是积极践行郑毓信教授所指出的解题教学的“第三个关键”—努力促进学生“就题论道”.
参考文献:
[1] 涂荣豹,陈嫣.数学学习中的概括[J].数学教育学报,2004(1):17-22.
[2] 马进.高中数学核心素养培育视域下的项目式学习研究[J].数学之友,2022,36(2):73-75.

