基于动网格技术的飞机舱弹分离过程CFD/RBD耦合数值仿真

徐学文，肖支才，曲 凯

（海军航空大学，山东 烟台 264001）

0 引言

1 仿真计算方程

飞机发射/投放弹是现代化战争中重要的作战活动和军事打击手段。随着第5代战斗机的研制成功及军事应用，为提高战斗机的隐身功效，战斗机均采用内埋舱贮式发射导弹与投放炸弹。

在飞机打击目标过程中，飞机舱弹分离过程非常复杂：在飞机弹舱处产生流动分离、激波干扰等复杂的流动现象，在舱外表面还存在强烈的气流剪切层[1]；飞机与导弹/炸弹分离之后，导弹/炸弹将进行六自由度运动，飞行姿态极易受外界气流、作用力和激波的影响产生较大变化，这不仅对载机的安全性造成严重的威胁，而且还对投放安全、姿态稳定与打击精度造成影响[2]。因此，研究飞机舱弹分离过程，提高舱弹分离品质与导弹/炸弹的打击精度，具有重要的军事意义。

当前，国内外对舱弹分离问题的研究主要采用风洞试验[3-4]、飞行试验[5-6]和数值仿真[7-8]3 种方法，其中，风洞试验和飞行试验存在研究成本高、威胁性大、耗时长等缺点。

近年来，随着计算机性能提高和动网格仿真技术进步[9-11]，数值仿真已成为科学研究的主要手段。因此，本文采用计算流体动力学（CFD）和刚体动力学（RBD）模型耦合求解的数值仿真方法[12]，基于动网格技术模拟飞机舱弹分离过程，研究炸弹投放分离后俯仰角度的变化。

1.1 RBD方程

飞机在投放弹时保持匀速直线飞行，然后打开舱门，把要投放的炸弹从弹舱弹射出去。抛射瞬间，炸弹受到重力FG、抛射力FS和抛射力矩MS的作用，脱离贮存架，炸弹做六自由度运动。舱弹分离后，炸弹还要受到来流气体压力FP、黏性摩擦力Fu和气动力矩Md的作用。在炸弹运动的数值模拟过程中，不考虑炸弹的材料特性（假设为刚体），将炸弹在空间的运动看作是导弹质心的移动和导弹绕质心的转动的合成[13]，在惯性坐标系(x,y,z)下可用线速度vc(vx,vy,vz)和角速度ωc(ωx,ωy,ωz)来描述，且它们都是时间t的函数。同时，在炸弹上建立以质心为原点的随动体坐标系(xb,yb,zb)，如图1所示，ocxb为弹体轴线，指向头部，oczb在弹体中心对称面内垂直ocxb轴线，指向下方。

图1 炸弹受力及坐标系Fig.1 Force and coordinate system of bomb

惯性坐标系下炸弹质心平移运动方程为：

式（1）中：v̇c为惯性坐标系下炸弹质心的加速度；m为炸弹质量；F为炸弹质心处所受外力。

体坐标系下炸弹角运动方程为：

式（2）中：ω̇b为体坐标系下炸弹的角转动加速度；L为转动惯量；Mb为力矩矢量。体坐标系炸弹角运动方程可以通过坐标转换矩阵I转换成惯性坐标系下运动方程。

在仿真计算中，通过对式（1）（2）积分就可以确定炸弹质心的位置和运动方向。设和分别表示当前第n时间步质心的位置和方向，则下一个时间步(n+1)时质心的位置及方向为：

刚体的位置矢量根据瞬时角速度ωc转动来确定，对于有限的转动角Δθ= |ωc|⋅Δt，炸弹位置矢量xr相对于质心xc表示为：

式（5）中，eθ、er为单位矢量。

1.2 CFD方程

本文涉及对RBD的数值模拟，因而使用任意拉格朗日-欧拉方法（Arbitrary Lagrangian-Eulerian，ALE）描述的N-S 方程，对流场进行描述[14-16]。在CFD 惯性坐标系下，对于边界移动的任意控制体积V上的标量φ（质量ρ、速度u、能量E），非定常守恒型动网格流场计算方程为：

式（6）中：V(t)为空间中大小和形状都随时间变化的控制体积；ρ为流体密度；∂V( )t为控制体积的运动边界；ug为运动网格的运动速度；u为流体速度矢量；Γ为耗散系数；Sφ是标量φ的源项。

湍流模型采用计算精度比较高、应用比较广泛的k-ε二方程模型。

k控制方程：

ε控制方程：

式（7）（8）中：P为湍流动能产生项；vt为黏性系数，vt=，而μt=；Cμ、Cε1、Cε2、σε和σk为模型系数。

另外，为使方程组封闭，还有气体的状态方程：

式（9）中：pg为气体压力；R为气体常数；T为气体温度，单位K。

2 数值仿真方法

2.1 流场网格离散模型

本文为简化计算，仅考虑炸弹质心运动位置及俯仰角度变化，不考虑炸弹滚动、偏航角度，因此，这里采用二维流场仿真计算。选择飞机舱弹分离的炸弹部分运动区域作为仿真区域，采用有限体积法[17]的非结构化网格离散这个区域，最终所建立的流场仿真区域离散网格及边界如图2所示。将流场来流方向设置为压力进口边界，出流方向设置为远场边界。

图2 流场离散网格Fig.2 Discrete grid of flow field

2.2 动网格仿真技术

为保证流场仿真区域内刚体（炸弹）气动力的计算精度，首先，在弹体周围生成流体边界层，让流体边界层随着弹体一起运动，保证弹体周围的边界层不变，并且在弹体附近区域加密计算网格[15]。在计算过程中，为避免由于刚体运动导致流场区域网格扭曲，品质变坏，严重影响仿真精度的情况发生，这里采用弹性光顺法（smoothing）和局部网格重构法（remeshing）2 项动网格技术[17]。弹性光顺法能够保证整个仿真区域网格节点像弹簧连接的网格系统一样，在计算时间步更新后，重新达到新的平衡位置，减少全域网格扭曲变形；局部网格重构法保证了刚体附近局部网格扭曲率或尺寸超过设定标准时，局部网格将被重新划分，从而减少了局部区域网格过大变形，但同时，局部网格间连接属性、节点数量和连接关系发生改变。应用弹性光顺法和局部网格重构法后，网格质量得到显著改善。流场仿真网格如图3所示。

图3 网格重构后的流场仿真网格Fig.3 Flow field simulation network after grid reconstruction

2.3 仿真耦合方法

本文采用CFD和RBD方程耦合求解来仿真舱弹分离过程[18-19]：首先，利用CFD方程计算出某一时刻仿真区域流场参数分布，获得流场中炸弹所受气动力和气动力矩，将其传递给RBD方程以获得炸弹对气动力的响应；然后，通过RBD 方程计算出下一时刻的炸弹运动位置和姿态，根据这些信息更新计算网格（经过反复迭代直至满足动网格设置标准）；再进行下一时刻的CFD方程计算以获取新的气动力；重复以上耦合过程，直至计算完毕。

3 计算结果与分析

本文仿真的刚体对象——炸弹质量m为500 kg，转动惯量Lzz为500 kg∙m2，飞机飞行马赫数为0.76，初始流场区域划分的网格单元数为19 596，最小单元面积为1.827×10-2m2，最大单元面积为1.908 m2。在舱弹分离时刻，飞机向炸弹施加了抛射力（转换到重心上为Fcx、Fcy、Mcz），作用时间0.3 s。在Fcx=-10 000 N、Fcy=-8 000 N 下，Mcz分别为0 N∙m、2 200 N∙m、-2 200 N∙m，计算不同力矩下炸弹姿态变化。

当Mcz=0 N∙m 时，炸弹在抛射力Fc作用下加速离开弹舱向下运动，出舱瞬间在外界干扰下极易发生弹体反转，如图4所示。在机舱舱门刚打开，炸弹离开原位瞬间，由于弹体上下表面受外界气流压力不均衡，炸弹头部微微向下摆动（转动角度为2°），0.4 s 弹体完全出舱脱落飞机边界层气流的影响，在外界气流作用下，弹体周围压力分布如图5 所示。弹体上气体压力、黏性力合成出1 个顺时针气动力矩推动弹体开始做顺时针转动，弹体转动角度由正值变为负值，如图6 所示。在1.38 s 时转动角度达到-90°，头部朝上，转动速度仍为负值，弹体在转动惯性作用下姿态角度继续增大。此后，炸弹在重力、气动力作用下，弹体姿态角度迅速调整到-270°，弹头向下。

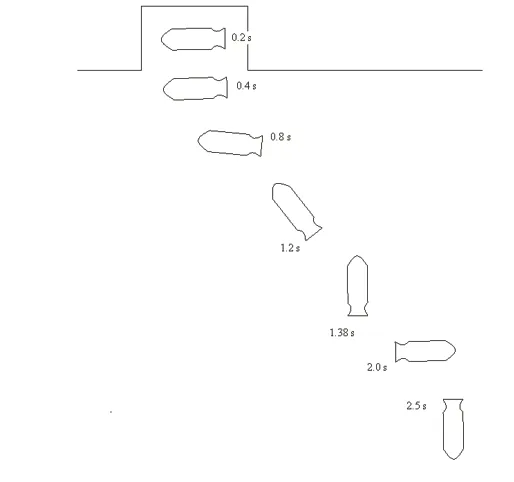
图4 炸弹下落轨迹及姿态（Mcz=0 N∙m）Fig.4 Falling track and attitude of bomb(Mcz=0 N∙m)

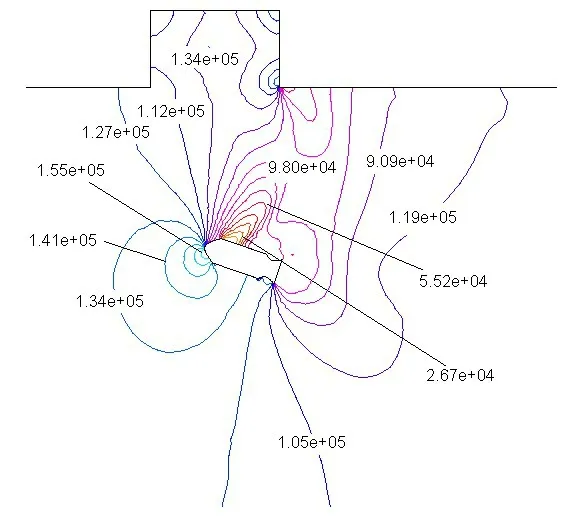
图5 弹体周围压力分布Fig.5 Pressure distribution around the bomb

图6 弹体姿态角度变化Fig.6 Attitude angle change of bomb

当炸弹出舱时向其施加1 个正向力矩作用（Mcz=2 200 N∙m），弹体获得了1 个逆时针转动角速度。炸弹出舱后，在重力、气动力矩的作用下，弹头迅速向下摆动，并且转动角速度也迅速增大，1.1 s 弹体转动角度就达到90°，弹头摆正到垂直向下打击姿态，如图7所示。此后，弹体主要在惯性力矩作用下，围绕垂直打击姿态（炸弹轴线与重力作用线重合）做左右调整摆动，打击姿态迅速稳定。

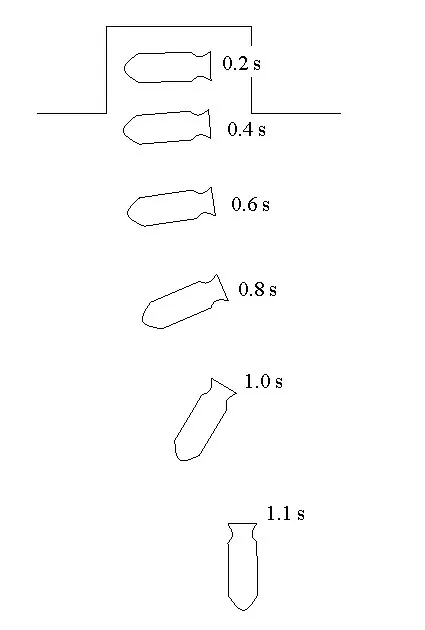
图7 炸弹下落姿态（Mcz=2 200 N∙m）Fig.7 Falling attitude of bomb(Mcz=2 200 N∙m)

当炸弹出舱时向其施加1 个负向力矩时（Mcz=-2 200 N∙m），炸弹出舱后，弹体转动角度、转动角度顺时针迅速增加，1.12 s 时转动角度达-90°，2.23 s时弹体转动到-270°，导弹垂直打击姿态如图8所示。

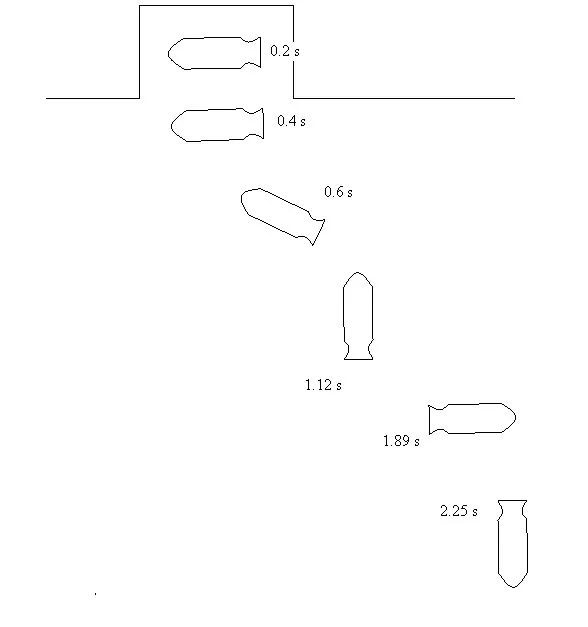
图8 炸弹下落姿态（Mcz=-2 200 N∙m）Fig.8 Falling attitude of bomb(Mcz=-2 200 N∙m)

4 结论

本文基于网格弹性光顺-重构的动网格技术，将CFD与RBD方程耦合，仿真计算了炸弹从飞机舱分离后姿态角度变化历程，仿真过程及结果表明：

1）采用弹性光顺法和局部网格重构法相结合的动网格技术，能够有效地避免刚体运动引起的网格畸变，可显著提高网格品质和计算精度；

2）在舱弹分离时，向炸弹施加不同的力矩，弹体姿态调整方向是不一样的，当向其施加1 个正向的抛射力矩，有助于炸弹在下降过程中快速地摆正到垂直打击姿态，缩短姿态调整时间。