一种多目标区域多轨道星座设计方法

李伟建，张建勋，王海锋，刘旭光

（酒泉卫星发射中心，甘肃 酒泉，732750）

0 引言

对地观测卫星是航天发射载荷的重要组成部分，也是各航天强国发展的优先方向。在天基资源有限的情况下，建立适应多目标区域观测任务的星座将更具灵活性和弹性。因此，在星座设计时，应综合考虑星座对多个目标区域的观测需求。

围绕星座设计方法的研究很多，有的侧重特定任务需求[1-5]，有的侧重特定轨道类型[6-7]，有的侧重对轨道进行优化设计[8-9]。总体而言，星座设计有两种思路：一种是从需求出发，也就是根据用户对星座的性能需求来设计星座，设计域较为广泛，容易设计出符合用户需求的星座；另一种是从供给端出发，将运载器能力作为硬性约束，在运载器能力范围内开展星座设计，有时不容易求得符合用户需求的星座，可能要牺牲性能需求，或以增加成本为代价。

目前，大多数的研究都是基于需求的，如基于重访时间[1]、星座覆盖率[10]等各种星座性能指标研究设计方法。其实从供给端出发，考虑运载器实际能力的星座设计更加具有现实意义，而将需求与供给综合考虑进行星座设计则更加全面、科学。

针对多目标区域观测任务需求，结合现有运载资源确定轨道类型，选取设计变量，在重访时间计算方法的基础上，采用多层嵌套变量搜索的方法开展星座设计，解决面向多区域观测任务的多轨道星座设计问题，为星座快速设计、发射任务快速规划等提供技术途径。

1 多区域多轨道星座设计任务分析

为了充分利用资源，提高星座效能，在星座设计时，须要综合考虑多个目标区域的观测要求，也就是在设计星座时尽可能多地兼顾各个目标区域的观测要求。如图1 所示，卫星半视场角为η，轨道高度为h，所设计的卫星轨道与星座能实现对地面各目标区域每天M次以上的观测，最大重访时间小于T。

本文基于多个目标区域的一体化观测需求，根据运载器现有能力，开展星座设计。在轨道类型选择时，主要选用低倾角和太阳同步轨道：一方面是由于快速响应运载器一般适应发射的轨道类型是低倾角和太阳同步轨道；另一方面是由于这2 种轨道类型有各自的优点，如低倾角轨道具有更快重访、时间遍历等特性，适合针对特定纬度带的观测任务[11]，太阳同步轨道能保证航天器飞经同纬度的地方时平太阳高度角相等，适合光学卫星的观测任务[12]。选定轨道类型后，须要确定的设计变量主要为低倾角轨道的高度和轨道倾角、太阳同步轨道的高度。

为了简化问题，2 种轨道类型均选用Walker 星座作为设计的起点，该星座参数包括星座卫星数N，轨道面数P，相位因子F。根据这组参数，在确定了1颗种子星后，便能形成整个星座。因此，设计变量从6N个变为9个，N>1。考虑到Walker星座的特点，令P=N，F=1，种子星的偏心率、升交点赤经、近地点幅角、平近点角为0，这样须要考虑的设计变量除了前述的3 个外，还有低倾角轨道、太阳同步轨道的卫星数量。假定星座卫星的总数已知，最终的设计变量可确定为低倾角轨道的高度、轨道倾角、卫星数量，太阳同步轨道的高度。

2 星座设计方法及流程

从上节的分析可以看出，面向多区域的多轨道类型星座设计是1个多变量的设计问题，而星座的性能，如上文提到的重访时间，与设计变量间很难建立显式的函数关系，在不具有任何先验信息的情况下，采用多层嵌套变量搜索方法更为自然，在设计域内进行搜索，找到符合要求的解，或者全空间搜索后进行结果统计分析，获得较优解。下文将先说明重访时间的计算方法，再提出基于多层嵌套变量搜索的星座设计流程。

2.1 重访时间计算方法

为了计算重访时间，须要通过轨道外推算法、星下点轨迹计算、探测区域算法、目标区域离散化等进行联合求解，具体求解过程如下。

2.1.1 轨道外推算法

根据对卫星受力考虑的精细化程度不同，产生了多种轨道动力学模型，也就有了多种卫星轨道外推算法，如J2摄动[13-14]、J4摄动[14]、Simplified General Perturbations（SGP4）[15]、High-Precision Orbit Propagator（HPOP）[16]等。1 个高精度的外推算法是卫星轨道设计的前提，这里采用考虑J4摄动的轨道外推模型。

设航天器的位置矢量为r=(x,y,z)，r= |r|。对于近地轨道，地球摄动的主要因素是地球的扁状。四阶带谐项引力位摄动函数可以写为[17]：

式（1）中：μ为地心引力常数；Re为地球平均赤道半径；φ为地心纬度；J2、J3、J4为摄动模型系数，J2=-0.001 082 616，J3=2.538 81×10-6，J4=1.655 97×10-6。计算赤道惯性坐标系下位函数的梯度，可以得到航天器在赤道惯性直角坐标系下的摄动加速度分量，将其叠加到二体模型，从而可以得到考虑J4引力摄动的轨道递推模型为：

2.1.2 星下点轨迹

考虑地球旋转时，t时刻的星下点可用其地心纬度、经度(φ,λ)描述如下：

式（3）（4）中：i为轨道倾角；u为纬度幅角；Ω为升交点赤经；Sˉ(t)为格林尼治平恒星时。

式（6）中，JD(t)为计算时刻t对应的儒略日。

2.1.3 探测区域算法

式（7）中：dσ为对地覆盖角，Re为地球半径，两者相乘为覆盖区域半径；η为卫星半视场角；h为卫星轨道高度。

2.1.4 目标区域离散化

若目标区域为圆形区域，如图2所示。

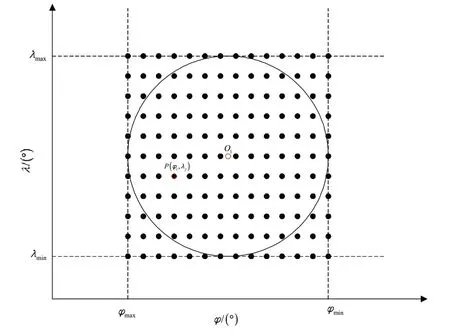
图2 圆形目标区域离散化示意图Fig.2 Diagram of discretization of circular target region

假设该区域的圆心为O1，半径为R，先将区域(φmin,φmax)×(λmin,λmax)划分为m×n的点阵，对于点阵中的任意点P，其坐标为(φi,λj)，则圆形目标区域包含的离散点可由下式确定：

式（8）中，‖ ⋅‖ 表示求2点间的距离。

若目标区域为矩形区域，如图3所示，与圆形区域同样处理。对于矩形区域P1P2P3P4中任意点P的坐标(φi,λj)满足以下关系：

图3 矩形目标区域离散化示意图Fig.3 Diagram of discretization of rectangular target region

式（9）中，“×”表示求两矢量的叉乘。

2.1.5 卫星覆盖目标区域的判断标准

根据卫星载荷性能参数，联合式（2）～（7）计算，可以确定当前时刻点卫星对地覆盖情况，如图4所示。

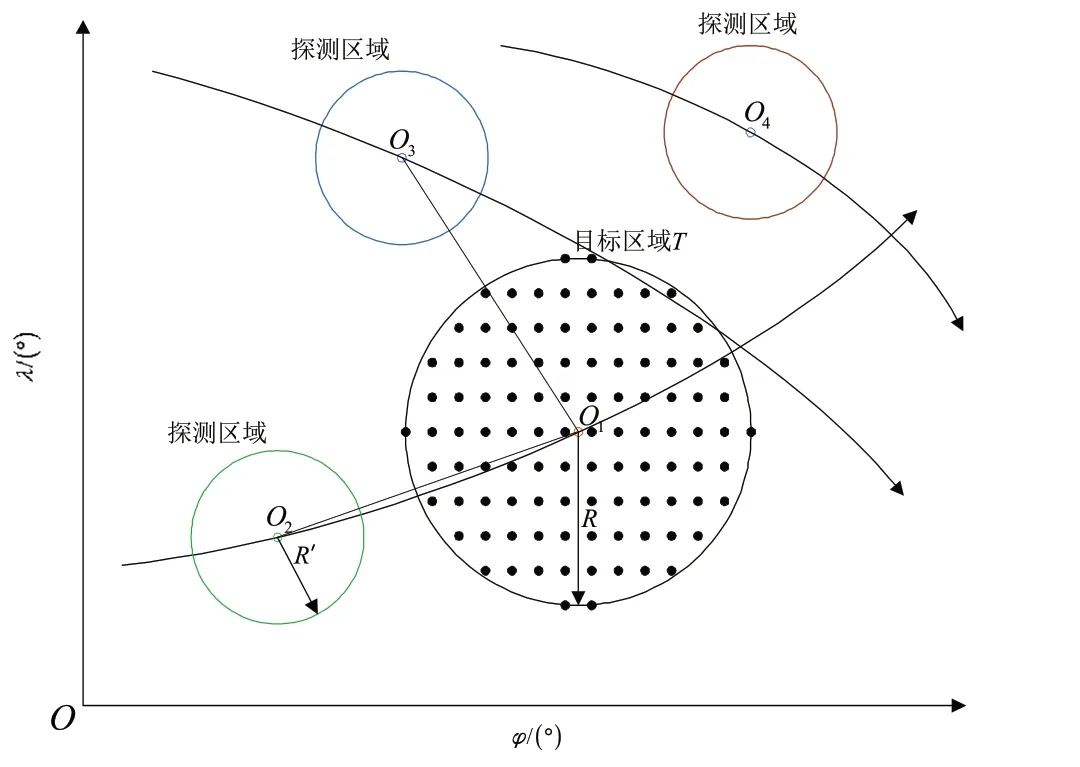
图4 卫星对地覆盖区域示意图Fig.4 Diagram of satellite coverage regions

从图4 可以看出，当卫星的探测区域沿着星下点轨迹运动，若要实现卫星对目标区域的覆盖，必须满足目标区域T内的点出现在卫星的探测区域内这一条件，如图中的O2、O3两轨能覆盖目标区域，而O4轨无法覆盖目标区域。为了判断目标区域T内的点是否在卫星的探测区域内，定义探测区域中心O到目标区域点集T的距离作为卫星对目标区域覆盖的判据。因此，卫星能覆盖目标区域的条件为：

式（10）中，O点的坐标就是星下点轨迹的坐标。

2.1.6 重访时间计算

设图4 中O2、O3为连续2 次探测到目标区域，记O2探测到目标区域的起始时间为t1，O3探测到目标区域的起始时间为t2，则重访时间为|t2-t1|。

不论目标区域是圆形区域还是矩形区域，根据卫星对目标区域覆盖的条件，确定t1的条件为：

同理可得确定t2的条件为：

2.2 星座设计流程

星座设计的总体流程如图5所示。

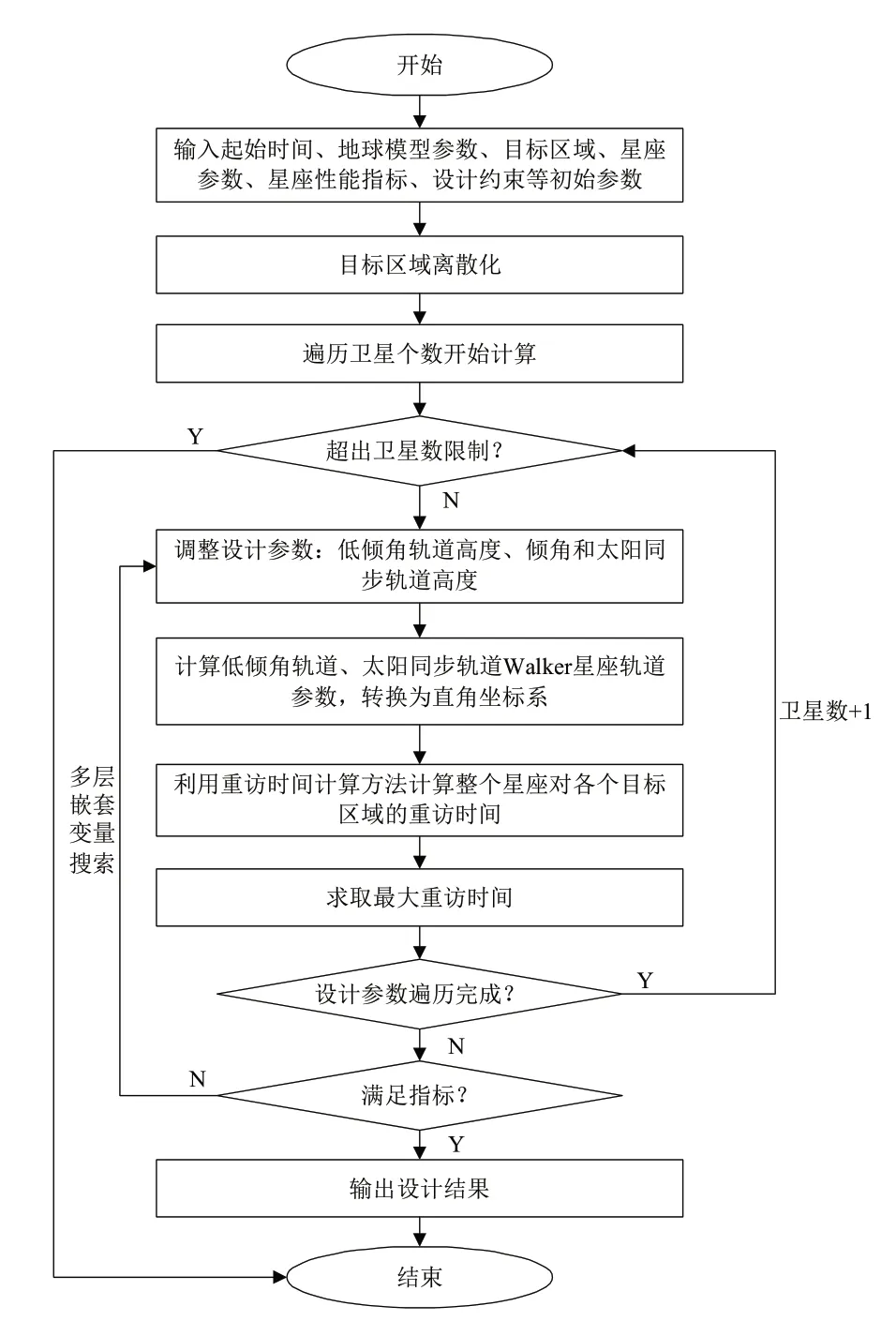
图5 星座设计流程图Fig.5 Constellation design flow diagram

该流程包含以下步骤。

1）输入计算的初始条件。包括历元时间、地心引力常数、地球平均赤道半径、摄动模型系数、目标区域坐标、卫星总数、相位因子、每个轨道内卫星数、偏心率、升交点赤经、近地点幅角、平近点角、最大重访时间要求值、设计变量的上下限、卫星半视场角等。

2）利用公式（8）（9）对目标区域离散化，获得目标区域点集Ti。

3）根据设计变量初始值和初始条件，确定低倾角轨道Walker星座轨道参数n1组，太阳同步轨道Walker星座轨道参数n2组，并将轨道初值转换为直角坐标形式。

4）利用2.1节中重访时间的计算方法，计算n1+n2构成的星座对每个目标区域Ti的重访时间，并求出最大值（这里的最大值是先对单个目标区域求最大值，再对3个目标区的最大值求其中最大）。

5）判断是否满足最大重访时间指标要求。若满足，则输出设计参数和最大重访时间值的结果；若不满足，则调整设计参数、低倾角轨道卫星数量，返回第3步，重新计算。

3 设计实例及结果分析

3.1 设计实例的初始条件

以观测纬度在[9°，35°]区间内低纬度地区的目标为例进行卫星轨道和星座设计，主要初始条件如表1所示。

表1 初始条件值Tab.1 Ⅰnitial condition values

3.2 设计结果及分析

根据表1 提供的初始条件，运用图5 中的编程算法，可以对此观测任务进行轨道和星座设计和分析。迭代搜索时，取轨道高度步长为20，取轨道倾角步长为2，共进行了3 630次计算，获得了2 707个满足最大重访时间要求的可行设计结果。当低倾角轨道和太阳同步轨道卫星数量确定时，求出可行设计结果里最大重访时间中的最小值，其对应的设计参数如表2 所示。

表2 卫星分配数量确定的情况下最大重访时间最小的设计结果Tab.2 Design results when maximum-revisit-time is minimum in the case of satellite quantity determined

从表2可以看出，如果只以重访时间为指标要求，则第5组参数设计结果为“较优”。当低倾角轨道卫星数量增多时，可行设计结果呈增多的趋势，最大重访时间也有变小的趋势。可见，增加低倾角轨道卫星数量对满足多个区域观测重访时间指标要求是有利的。如果考虑我国现有发射场位置，酒泉和太原发射场较适合发射太阳同步轨道，西昌发射场较适合发射低倾角轨道，那么从完成发射任务的角度而言，选择第3组参数也是合适的。

4 结论

多区域观测任务在应急处突、灾害监测、热点事件追踪中有重要的潜在应用价值。因此，面向多目标区域的星座设计是需要解决的一类重要问题。本文重点分析了重访时间的计算方法，并基于多层嵌套变量搜索的方法提出了星座设计的流程和算法，该方法能够实现低纬度多区域观测任务星座的快速设计，为发射任务快速规划提供技术支持，方法也充分考虑运载器的实际能力和发射场资源，更加具有现实意义。