基于生成对抗近端策略优化的机动策略优化算法

付宇鹏，邓向阳，2，朱子强，高 阳，张立民

（1.海军航空大学，山东 烟台 264001；2.清华大学，北京100084）

0 引言

自20 世纪50 年代以来，空战智能博弈一直是军事研究的重点之一。在诸多空战机动策略、姿态控制优化方法研究中，基于人工智能技术的算法取得了长足进步[1-5]。随着计算机硬件算力的提升和算法的进步，深度强化学习（DRL）技术以其优秀的逼近能力成为近年来的研究热点，其在面对复杂状态空间问题时仍能获得高水平策略模型。

传统强化学习算法效率和效果与任务的奖励函数设计密切关联，但空战博弈态势复杂，且六自由度（6-dof）飞机模型具有高阶非线性的特点，因而在训练初期，智能体很难获得正向奖励，致使算法难收敛。模仿学习技术则直接利用专家经验数据生成策略，在自动驾驶、无人机导航控制、机器人等领域被广泛应用[6-9]，主要分为行为克隆[10]、逆强化学习[11]、对抗模仿学习[12]3 类算法。但这些算法中，智能体依靠示例数据学习策略，对于空战博弈这类目标不明确的环境表现不佳。因此，将模仿学习和强化学习相结合的算法成为这类环境中生成智能体策略的研究热点[5，13-15]。

本文基于强化学习、模仿学习技术在飞行控制、智能博弈等方面的研究[2，4-5]，针对传统强化学习算法在生成空战机动策略时存在收敛效率低、专家经验利用不足的问题，提出了生成对抗式近端策略优化算法（GA-PPO）。在传统PPO 算法的策略-价值网络（Actor-Critic）框架基础上，增加判别器（Discriminator）网络，用来判断输入状态-动作是否属于当前策略或专家策略，在策略训练时约束当前策略向专家策略方向更新。

1 研究背景

1.1 近端策略优化算法

强化学习算法包括基于价值、基于策略和二者结合的Actor-Critic 方法。本文以Actor-Critic 方法为基础。Actor网络即策略网络，记为πθ( )st，其中，st表示t时刻状态，θ表示策略网络参数，策略网络输出动作at～πθ(st)；Critic 网络即价值网络，记为Vφ(st)，φ表示价值网络参数，价值网络用来估计当前策略的回报Rt，表示为：

式（1）中：E(⋅)为数学期望；γ为折扣系数，确保马尔科夫决策过程能够收敛；r为奖励函数，通常在实际环境中根据专家经验设计。强化学习算法目标是使回合回报最大化。在诸多算法中，TRPO[16]、PPO[17]等算法稳定性高，收敛效率高，成为了典型的基线算法。

以PPO2 算法为例，其采用优势函数Aθ来表示策略优劣，以减小方差，提高算法稳定性。Aθ定义为：

实际实现时，定义Ât来估计Aθ，采用使用较为广泛的广义优势估计（GAE）方法[18]，定义为：

其中，δt=rt+γV(st+1)-V(st)，参数λ用来平衡方差和偏差。

此外，算法中利用重要性采样方法（important sampling）直接剪裁旧策略与新策略的概率幅度，记为ct(θ)=πθ(at|st)/πθ,old(at|st)。因此，得到PPO2 算法的损失函数表示为式（4）～（6）。

1.2 生成对抗模仿学习算法

生成对抗模仿学习（GAⅠL）算法启发于最大熵逆强化学习（ⅠRL）和生成对抗网络（GAN）。在on-policy算法（如TRPO、PPO等算法）框架基础上，设计判别器Dω(st,at)，用来判断输入的采样数据是生成于专家策略还是当前策略。GAⅠL 算法目标，可理解为匹配当前策略分布与专家策略分布，使判别器无法区分当前策略和专家策略，其损失函数定义为：

式（7）（8）表示在GAⅠL算法中：首先，对当前策略πθ和专家策略πE采样，更新判别器参数ω′←ω；而后，以最大化判别器输出更新策略网络参数θ，此处可将Dω′(s,a)类比于强化学习算法中的状态-动作价值函数Q(s,a)。

由于GAⅠL 算法依靠专家数据生成策略，当该数据集包含的策略非最优，或无法达到目标时，生成策略性能将无法保证。因此，本文将强化学习环境探索优势与模仿学习的策略约束优势相结合，提出生成对抗式近端策略优化算法。

2 GA-PPO算法

GA-PPO算法框图见图1。模型包含价值网络、策略网络和判别器网络，部署时只保留策略网络；经验池包含示例经验池和回合经验池，示例数据池中的轨迹数据三元组()由人机对抗和基于规则模型的机机对抗产生。回合经验池中存储当前策略与环境交互所产生的轨迹四元组(st、at、st+1、rt)，每回合训练结束后，回合经验池清空。图中包括3 类数据流：环境交互数据流，当前策略与环境交互，生成轨迹数据存入回合经验池；DA网络更新数据流，回合结束后，根据式（7），利用梯度下降方法更新判别器网络参数，而后，根据式（8）更新策略网络参数，从而约束当前策略分布向专家策略收敛；AC网络更新数据流，与PPO算法流程相同，根据式（8）更新AC网络。

图1 GA-PPO算法框图Fig.1 Framework of GA-PPO algorithm

为提高算法收敛速度和稳定性，采用分布式并行计算方式，设置n个分布式rollout worker 和1 个中心learner。Rollout workers与环境交互，存储回合轨迹数据；回合结束后，计算各自策略梯度并回传learner 进行梯度累加，更新网络参数后，广播给各rollout worker，采集新一轮数据。

算法流程如图2 所示。首先，建立示例经验池DE={τ1,τ2,...,τn} ，其中τn表示第n条飞行轨迹，即τn=。初始化各网络参数和算法超参数。每回合结束后，采样DE和，计算策略梯度和，由learner累加梯度并更新网络参数，最终，输出最优策略网络参数θ*。

图2 GA-PPO算法流程Fig.2 Flow of GA-PPO algorithm

3 实验仿真环境设计

实验仿真环境采用OpenAⅠgym 平台框架，飞机空气动力学模型采用JSBSim开源平台的F-16飞机模型，其内部包含基本增稳系统。飞机在高空飞行过程中，机动动作由控制升降舵、副翼、方向舵和油门完成，因此，策略网络输出为舵面偏转角度和油门开度at={δel,δai,δru,δth}。

对抗过程中，红方由策略网络控制，蓝方由基于PⅠD 控制器的简单规则模型控制。为简化实验复杂度，双方态势全透明，设计状态向量st为：

式（9）中：ψ、θ、φ为飞机自身姿态角；θ̇为俯仰角速度；φ̇为当前滚转角；h为自身当前高度；V、ΔV、ΔX分别为NED 坐标系下的红方和蓝方的速度矢量、速度差矢量和相对位置矢量；αATA为方位角；αAA为目标进入角。st均归一化处理。

为保证算法收敛，一般设计较为稠密的奖励函数。本文主要考虑角度优势、能量优势和满足发射条件等方面，因此，设计奖励函数rt为：

式（10）中，η代表权重。此外，还应考虑飞机稳定飞行和保证在指定空域飞行的限制条件，因此，引入边界惩罚项，避免飞机诱导坠地等错误决策出现。

4 系统仿真

仿真中，红蓝双方初始高度1～9 km，初始相对水平距离±10 km，初始速度150～300 m/s，初始任意姿态，仿真步长20 ms，每回合5 min。算法中超参数设计如表1所示。DAC网络结构均采用全连接结构，其中隐藏层激活函数均为ReLu 函数，策略网络输出层激活函数为tanh 函数，判别器网络输出激活函数为sigmoid函数。损失函数采用Adam方法更新梯度[19]。

表1 GA-PPO算法参数设置Tab.1 Parameters of GA-PPO algorithm

图3 给出了回报函数的仿真结果。仿真中，首先利用示例数据对策略模型进行行为克隆预训练，避免智能体在训练初始阶段不收敛。实验中，对比了PPO算法、PPO-SⅠL[20]算法和本文的GA-PPO 算法。GAPPO-1中αθ为常数，GA-PPO-2表示αθ随仿真回合增加逐渐降低，即训练初期通过模仿学习提高智能体训练效率，训练后期通过强化学习提高其环境的探索能力。结果显示，GA-PPO 算法的收敛效率和最终回报要高于PPO 算法和PPO-SⅠL 算法。在约200 回合前，GA-PPO 算法需要训练判别器，因而回报函数略有波动，而后快速升高。GA-PPO-1 算法在训练中始终存在示例约束，因而波动较GA-PPO-2更小。

图3 回报函数仿真曲线Fig.3 Simulation curve of return function

图4 给出了价值函数的仿真曲线，即价值网络输出均值仿真，表示约10 s仿真步长的策略价值。为了提高比较的准确性，价值网络输入均为示例数据采样。结果表明，GA-PPO 算法较PPO-SⅠL 算法收敛速度更快，原因在于智能体状态空间探索的概率分布更接近示例数据，因而价值网络更新方向更稳定。

图4 价值函数仿真曲线Fig.4 Simulation curve of value function

图5 给出了根据公式（7）得到的判别器目标函数仿真曲线。该函数接近2 ln( 0.5) =-1.38，说明当前策略接近示例策略，即判别器无法区分当前策略和示例策略。GA-PPO-2 中，αθ逐渐减小，因而训练中强化学习算法的更新比重逐渐增加。尽管回报仍逐渐增加，但当前策略与示例策略分布偏差略有增加。结果说明，可以通过调节式（8）和式（5）中的αθ的比例来影响策略分布，选择智能体探索环境或模拟专家策略。

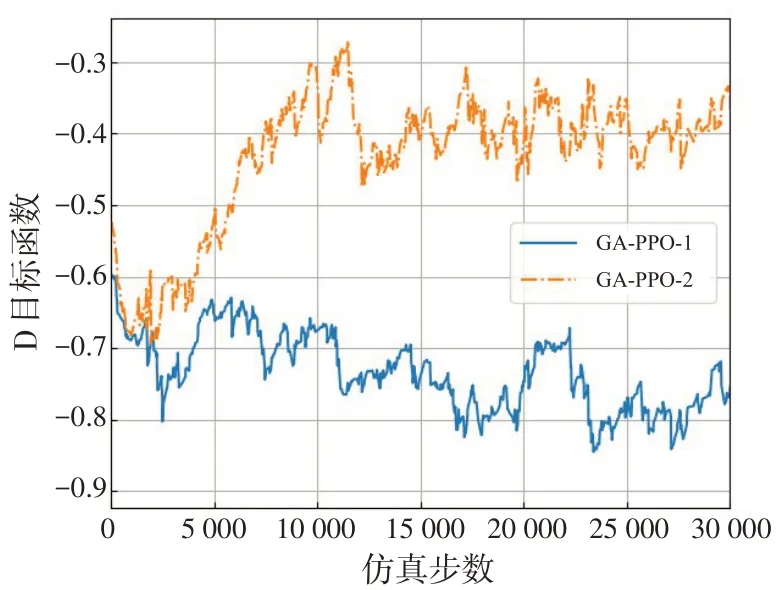
图5 判别器目标函数仿真曲线Fig.5 Simulation curve of D-object funtion of discrimination

图6给出了红蓝双方均使用GA-PPO生成策略的对抗态势图。红蓝双方初始态势均势，高度5 km，速度200 m/s，相向飞行。

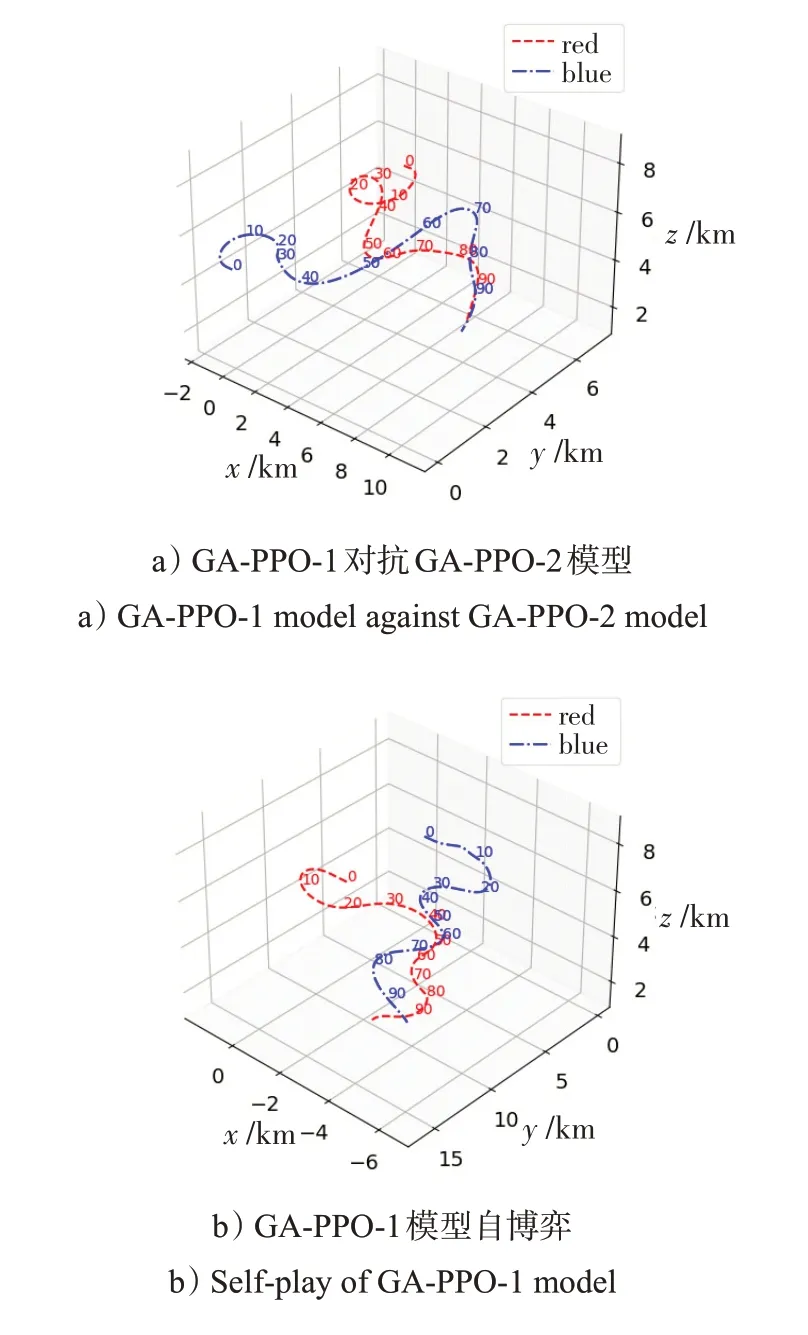
图6 空战博弈态势图Fig.6 Diagram of air combat play

图6 a）中，红方使用GA-PPO-1生成模型，蓝方使用GA-PPO-2 生成模型。10 s 时，双机对头有进入双环战趋势，而后双方相向飞行处于均势，20 s时红方选择半滚倒转机动迅速调转机头指向蓝方，蓝方处于劣势，爬升急转脱离未果，红方始终保持后半球优势；图6 b）中，红蓝双方均使用GA-PPO-1生成模型自博弈，双机交会后进入剪刀机动，均未能率先脱离，在双方使用相同策略下和初始均势开局情况下，最终收敛于纳什均衡点，与直观态势理解相一致。

5 结论

本文提出了1种基于GA-PPO的空战机动决策生成算法，能够利用示例数据约束策略优化方向，提高算法收敛效率。同时，结合强化学习环境探索能力，优化当前策略。结果表明，基于GA-PPO 算法的策略模型具有较高智能性，较符合专家经验。

但算法仍存在一些问题：一方面，利用强化学习技术探索环境能力受限于奖励函数，对空战态势评估函数准确性、引导性、稠密性要求较高；另一方面，示例数据的多峰或非最优性问题未得到根本的解决。此外在模型实际部署模拟器进行人机对抗时，应考虑对手变化带来的迁移问题，在未来工作中需要进一步优化。