具有非线性恢复率的随机SIQR模型的阈值动力学

孙乾乾，赵 宇，谭德君，张树文

(1.厦门工学院数据科学与智能工程学院，福建 厦门 361021；2.集美大学理学院，福建 厦门 361021)

0 引言

疫情的暴发对人们的生活产生了深远的影响[1]。纵观历史，也有许多其他大型流行疾病对人类的生命健康构成严重威胁，如1918年西班牙的大流感[2]、欧洲20世纪中世纪的大瘟疫[3]等。由于无法及时生产有效的疫苗以及病毒的快速变异，隔离被认为是控制传染病传播的有效方法[4-7]。此外，有效治疗是保障人类生命安全和减少疾病传播的重要方法[8]。但在疾病暴发期间，医护人员的数量、医疗设备、医院床位和药品的数量都是非常有限的[9-11]。因此，为了刻画医疗资源对疾病的影响，文献[11]提出非线性恢复率γ(b，I)=γ0+(γ1-γ0)b/(I+b)，其中：γ1、γ0分别是最大和最小的恢复率；I是染病者的数量；b是医疗资源。本文将在文献[5,11]研究的基础上，提出SIQR模型为

(1)

其中：S、Q、R分别是易感者、隔离者、恢复者的数量；N=S+I+Q+R是总人口的数量；A是新的易感者的输入率；β是疾病的传播速率；μ是自然死亡率；δ是隔离率；α1和α2分别是染病者和隔离者的因病死亡率；ε是隔离者的恢复率。

此外，大量实验和流行病学研究表明，病毒的活性、感染力与周围空气的湿度、温度等密切相关[12-15]。因此，在流行病的传播过程中，疾病的传播速率不可避免会受到环境随机波动的影响[16-19]。本文假设模型(1)的疾病传播速率β受到白噪声的干扰，即βdt→βdt+σdB(t)，然后得到的模型为

(2)

其中：σ是白噪声的波动强度；B是一维标准布朗运动。

1 主要结果及证明

在流行病模型的研究中，基本再生数R0是一个重要的量，它表示发病初期在一个全部是易感人群的环境中，一个染病者在平均患病期内所传染的人数。利用下一代矩阵可得到模型(1)的基本再生数为

R0=β/(γ1+δ+μ+α1)。

(3)

由此可知定理1。

定理1 模型(1)总是存在无病平衡点E0=(A/μ，0，0，0)。如果R0<1，则模型(1)的无病平衡点E0是局部渐近稳定的；如果R0>1，则E0是不稳定的。

定理2 如果R0>1，则模型(1)存在唯一的地方病平衡点E*(S*，I*，Q*，R*)。

证明由于模型(1)的地方病平衡点E*(S*，I*，Q*，R*)满足方程

(4)

容易验证I*满足方程

α1-α2I*2-α3I*=0，

(5)

其中：α1=Ab(β-(δ+μ+α1+γ1))；α2={β-[1-(μ+ε)/(ε+μ+α2)]δ-α1}(δ+μ+α1+γ0)；α3={β-[1-(μ+ε)/(ε+μ+α2)]δ-α1}(δ+μ+α1+γ1)b-A[β-(δ+μ+α1+γ0)]。当R0>1时，有α1>0且α2>0。由二次方程求根公式可知，方程(5)存在唯一的正解，即当R0>1时，模型(1)存在唯一的地方病平衡点，定理2证毕。

显然，当R0<1时，方程(5)可能存在两个正解，即模型(1)可能存在两个正平衡点。因此，模型(1)可能存在后向分岔。接下来应用中心流形定理来证明模型(1)在R0=1时发生后向分岔。

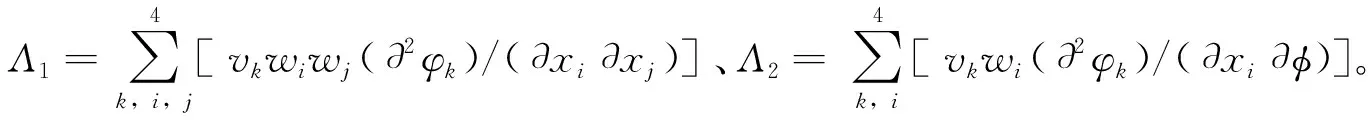
通过计算可得

(6)

且Λ2=(ε+μ+α2)/δ>0。然后，根据文献[20]中的定理4.1可得定理3。

定理3 如果Λ1>0，则模型(1)在R0=1处发生后向分岔。

为了方便理解，给出例1。

例1 首先取如下参数：A=30，μ=0.1，γ0=0.009 8，γ1=0.239 4，b=0.072，δ=0.104 6，α1=0.001 7，ε=0.239 4，α2=0.001 1，且令β在区间[0.133 71,0.467 985]内变化，使得R0在区间[0.30,1.05]内变化。由式(6)可得，Λ1=1.219 07>0。因此，根据定理3可知，模型(1)在R0=1处发生后向分岔(见图1)。

此外，令β=0.231 76，此时R0=0.52。根据定理3可知，模型(1)的解要么被地方病平衡点E*(282.160 667 5，8.179 298 012，2.512 641 915，6.980 705 454)所吸引，要么被无病平衡点E*(300，0，0，0)所吸引。这意味着，R0不足以完全确定基本的动力学行为，还需要考虑初始条件等其他流行病学因素(见图2)。

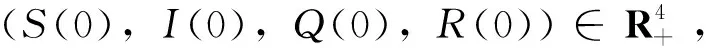
定理4的证明比较简单，详细的证明过程可参考文献[21]。

证明首先证明，对于任意的>0，总是存在ξ>0，使得对于任意的(S(0)，I(0)，Q(0)，R(0))∈Γ∩Oξ，其中，Oξ=(A/μ-ξ，A/μ)×(0，ξ)3，有

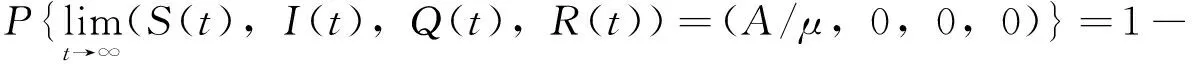
(7)

定义：f1(S，I，Q，R)=A-βSI/N-μS，g(S，I，Q，R)=σSI/N；f2(S，I，Q，R)=βSI/N-(γ(b，I)+δ+μ+α1)I，λ=β-(γ1+δ+μ+α1)。f1(S，I，Q，R)、f2(S，I，Q，R)和g(S，I，Q，R)在无病平衡点E0=(A/μ，0，0，0)的偏导数分别为：(∂f1)/(∂S)(E0)=-μ；(∂f1)/(∂I)(E0)=-β； (∂f1)/(∂Q)(E0)=0；(∂f1)/(∂R)(E0)=0；(∂f2)/(∂S)(E0)=0；(∂f2)/(∂I)(E0)=λ；(∂f2)/(∂Q)(E0)=0；(∂f2)/(∂R)(E0)=0；(∂g)/(∂S)(E0)=0；(∂g)/(∂I)(E0)=σ；(∂g)/(∂Q)(E0)=0；(∂g)/(∂R)(E0)=0。因此，f1(S,I,Q,R)、f2(S，I，Q，R)和g(S，I，Q，R)在无病平衡点E0附近的泰勒展开分别为

f1=-μS-βI+o；f2=βI-(γ1+δ+μ+α1)I+o；g=σI+o，

(8)

接下来证明，对于任意的(S(0)，I(0)，Q(0)，R(0))∈Γ，模型(2)的解(S(t),I(t),Q(t),R(t))总会在某一时刻进入区域Γ∩Oξ。定义停时τξ=inf{t≥0：S(t)≥A/μ-ξ}，并定义函数V1(S，I，Q，R)=C1-(1+S)C2，其中C1和C2是两个正常数，并且满足如下条件：1)对于任意的(S，I，Q，R)∈Γ，都有V1>0；2)C2>2；3)对于任意的S∈(0，A/μ-ξ]，有(1+S)(A-βSI/N-μS)+0.5σ2(C2-1)S2I2/N2≥0.5ξ。

然后，根据Dynkin公式可得：E[V1(S(τξ∧t)，I(τξ∧t)，Q(τξ∧t)，R(τξ∧t))]≤V1((S(0)，I(0)，Q(0)，R(0)))-0.5ξE(τξ∧t)。令t→∞，并根据Fatou引理可得：E[V1(S(τξ)，I(τξ)，Q(τξ)，R(τξ))]≤V1((S(0)，I(0)，Q(0)，R(0)))-0.5ξE(τξ)。

注意到，对于任意的(S，I，Q，R)∈Γ，V1是有界的，因此有

E(τξ)<∞。

(9)

最后，根据强Markov性质，由式(7)和式(9)可得，对任意的，对于任意的(S(0)，I(0)，Q(0)，R(0))∈Γ。定理5证毕。

证明定义函数H(S，I，Q，R)=M[1(S+I+Q+R)-lnI-2lnS]-lnS-lnQ-lnR-ln(N-A/(μ+α1+α2))-ln(A/μ-N)∶=MV1+V2，其中：V1=1(S+I+Q+R)-lnI-2lnS；V2=-[lnS+lnQ+lnR+ln (N-A/(μ+α+α))+ln (A/μ-N)]；1=(γ1+δ+μ+α1+0.5σ2)/A；2=(γ1+δ+μ+α1+0.5σ2)/μ；M是一个充分大的常数，使得

(10)

LV1≤-βS/N+(γ1+δ+μ+α1+0.5σ2)+2(-A/S+βI/N+μ+σ2I2/(2N2))+1A-1μN

(11)

并且有

LV2≤-A/S+β+μ+0.5σ2-δI/Q+(ε+μ+α2)-εQ/R+μ-(α1I+α2Q)/(A/μ-N)-

(α1(S+Q+R)+α2(S+I+R))/(N-A/(μ+α1+α2))+μ+α1+α2+μ。

(12)

根据式(10)～式(12)可得：LV=MLV1+LV2≤-2+M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2-A/S-δI/Q-εQ/R-α2I/(N-A/(μ+α1+α2))-α1I/(A/μ-N)。令ε是一个充分小的正常数，使得-2+M2β(μ+α1+α2)/A+0.5M2σ2(μ+α1+α2)22/A2≤-1，M2β(μ+α1+α2)/μ+0.5M2σ2(μ+α1+α2)2/μ2-min{A，δ，ε，α1，α2}/<-1。

然后将ΓD分成6个区域，即ΓD=D1∪D2∪D3∪D4∪D5∪D6，其中：D1={(S，I，Q，R)∈Γ：0

对于任意的(S，I，Q，R)∈D1，有

LV≤-2+M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2
≤-2+M2β(μ+α1+α2)/A+0.5M2σ2(μ+α1+α2)22/A2≤-1。

(13)

对于任意的(S，I，Q，R)∈D2，有

LV≤M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2-A/S
≤M2β(μ+α1+α2)/μ+0.5M2σ2(μ+α1+α2)2/μ2-A/≤-1。

(14)

对于任意的(S，I，Q，R)∈D3，有

LV≤M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2-δI/Q
≤M2β(μ+α+α)/μ+0.5M2σ2(μ+α+α)2/μ2-δ/2≤-1。

(15)

对于任意的(S，I，Q，R)∈D4，有

LV≤M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2-εQ/R
≤M2β(μ+α1+α2)/μ+0.5M2σ2(μ+α1+α2)2/μ2-ε2/3≤-1。

(16)

对于任意的(S，I，Q，R)∈D5，有

LV≤M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2-α2I/(N-A/(μ+α1+α2))
≤M2β(μ+α1+α2)/μ+0.5M2σ2(μ+α1+α2)2/μ2-α2/2≤-1。

(17)

对于任意的(S，I，Q，R)∈D6，有

LV≤M2β(μ+α1+α2)I/A+0.5M2σ2(μ+α1+α2)2I2/A2-α1I/(A/μ-N)
≤M2β(μ+α1+α2)/μ+0.5M2σ2(μ+α1+α2)2/μ2-α1/2≤-1。

(18)

由式(13)～式(18)可得，对于任意的(S(t)，I(t)，Q(t)，R(t))∈ΓD，有LV≤-1。因此，Markov过程(S(t)，I(t)，Q(t)，R(t))关于D是正常返的，定理6证毕。

2 数值模拟

根据C0VID-19的实际参数值来验证并扩展本文的理论结果。首先假设，武汉某一地区的常住人口总规模为10 000人，每个人的平均寿命为80 a，且每千人拥有5张病床，则自然死亡率μ=1/(365×80)=3.424 65×10-5，医院病床数b=50。假定新的易感者的输入率A=30，疾病的传播速率β=1.5。其他的参数取自文献[22]。总的参数取值为：A=30，β=1.5，μ=3.424 65×10-5，γ0=0.009 8，γ1=1/14，b=50，δ=0.104 6，α1=0.001 7，ε=0.239 4，α2=0.001 1。

接下来，假设随机模型(2)的初值(S(0)，I(0)，Q(0)，R(0))=(7 000，1 000，1 000，1 000)，并考虑白噪声强度σ对模型(2)动力学的影响。

3 结论