交换突变策略改进萤火虫算法的异构并行机调度

罗冬梅，陈玲清，张瑀鑫，黄兴旺

(集美大学计算机工程学院，福建 厦门 361021)

0 引言

经典的异构并行机调度问题(parallel machine scheduling problem，PMSP)[1]广泛存在于科学和工业生产中，包括印刷电路板制造[2]、半导体晶圆制造[3]的切割操作等应用领域。在云计算[4]、边缘计算[5]中通常还会涉及到作业排序的等待时间、作业数据传输时间等设置时间，并且由于设备的异构性，相当部分类型作业还会有序相关设置时间的异构并行机调度问题(the unrelated parallel machines scheduling problem，UPMSP)[1]。

在UPMSP问题中，优化目标通常是最小化任务完工时间。大多数问题需要使用两台或多台机器并行调度，在某些情况下，设置时间和处理时间同等重要，因而需要同等考虑。Paula等[6]第一次将可变邻域搜索算法(variable neighborhood search，VNS)用于求解高维的序相关设置时间的UPMSP问题。Vallada等[7]提出一种基于局部搜索增强交叉算子的遗传算法(genetic algorithm，GA)来求解UPMSP问题，该研究也考虑了机器和作业之间的序相关设置时间影响。Behnamian等[8]提出一个结合了蚁群(ant colony optimization，ACO)、模拟退火(simulated annealing，SA)和VNS算法的混合元启发式算法，求解同样考虑了序相关设置时间的UPMSP问题，使得任务完成时间最小化。Arnaout等的研究[8-9]使用增强的ACO算法在机器数多达10且作业数多达120的用例中求解序相关设置时间的UPMSP问题。Ezugwu 等[3]实现了一种改进的樽海鞘群算法(salp swarm algorithm，SSA)，得到与序列相关的UPMSP算法的新的复杂度结果。牛群等[10]基于改进的克隆选择算法实现了含调整时间的并行机调度，其性能较遗传算法和基本克隆选择算法都有所提高。但是上述算法在高维情况下，搜索性能有所下降。

标准萤火虫算法(firefly algorithm，FA)[11]具有超参数少、易实现等优点，在连续域数值优化问题中表现出了高效的性能。由于序相关设置时间UPMSP问题具有非确定多项式难的性质，求解难度大，而FA采用的吸引度因子存在快速减小情况，又容易面临提前终止搜索、达到局部最优的问题。为此，本文提出了一种基于交换突变策略改进的萤火虫算法(improved firefly algorithm based on mutation strategy，IFAMS)用于求解具有序相关设置时间的UPMSP问题。

1 数学建模

1.1 问题描述

本文所改进的求偶学习的萤火虫算法求解序相关设置时间的UPMSP问题描述如下：

a)该调度问题假定在时间零点有N个可用的作业待分配到M台异构的机器上处理，机器之间相互独立。

b)不存在抢占执行作业情况。

c)数据集中，由Pj，k表示的机器k处理分配到的作业j所需的时间，和由Si，j，k给出的机器k上的作业i之后处理作业j的序相关设置时间，都是先验和确定的。其中，i，j={1，2，…，N}，k={1，2，…，M}，通常Si，j，k≠Sj，i，k。

d)优化目标为最小化任务完工时间Cmax，因此该模型可以用(Pj，k|Si，j，k|Cmax)表示。

1.2 模型构建

本文采用基于混合整数规划(mixed integer programming，MIP)拓展的模型[1，3，7]来表示(Pj，k|Si，j，k|Cmax)模型，方便最小化任务完工时间Cmax的求解。为了描述该问题的数学模型，本文给出了部分符号定义：Cj—机器上最后一个作业j的完成时间；xi，j，k—在机器k上处理完作业i后立即处理作业j时为1，否则为0；x0，j，k—机器k首先处理作业j为1，否则为0；V—一个充分大的正数；APi，j，k—校正后的机器处理时间矩阵。

本文建立了(Pj，k|Si，j，k|Cmax)的数学模型为：

MinimizeCmax。

(1)

约束条件有：

5)Cj≤Cmax，∀j=1，…，N；

6)C0=0；

7)Cj≥0，∀j=0，…，N；

8)xi，j，k∈{0，1}，∀i=0，…，N，∀j=0，…，N，∀k=1，…，M。

其中：公式(1)的目标是最小化任务完工时间；约束条件1)确保作业只会被执行一次；约束条件2)表示每台机器最先被处理的作业数为1；约束条件3)确保每个作业最先被处理或者构成其他作业的紧后处理作业；约束条件4)用于计算各个作业的完工时间；约束条件5)将Cmax定义为必须大于任何其他作业完成时间的变量；约束条件6)确保虚拟作业0的完成时间为0；约束条件7)确保作业完成时间非负；约束条件8)定义了决策变量x的取值范围。

2 基于改进萤火虫算法的UPMSP

2.1 标准萤火虫算法

萤火虫的荧光亮度(相互吸引度)可表示为：βi，j(ri，j)=β0e-γri，j2。其中：ri，j是两只萤火虫xi和xj之间的欧几里德距离；β0表示初始吸引度因子，通常取值为1；参数γ表示光吸收系数的固定值，一般也取值为1。对于同一搜索空间随机选取的两只萤火虫xi和xj，它们之间的距离

其中：D代表问题的维数；d表示处于萤火虫位置向量的维数。

搜索过程中，萤火虫xj受更亮的萤火虫xi吸引，向xi移动，其位置更新方式为：xj(t+1)=xj(t)+βi，j(xi(t)-xj(t))+α。其中：t表示算法的迭代次数；α是步长参数，通常取值为[0，1]的随机数；是[-0.5，0.5]之间的随机数。

在FA的寻优过程中，所有萤火虫会向较亮的萤火虫移动，最终萤火虫个体将集结在最亮的萤火虫周围，完成寻优过程。

2.2 改进FA算法

仔细分析FA算法中的吸引度因子β随萤火虫距离r的变化可知，当这两个萤火虫之间的距离r较大时，β随r增加快速下降至近0，萤火虫间的吸引度快速下降，个体之间无法充分地进行信息交互，此时FA算法面临移动提前终止、萤火虫种群进化出现停滞的情况。一旦陷入局部最优，由于此时萤火虫不具备变异特性，将无法跳出。

本文在FA框架[11]的基础上，提出一种改进的萤火虫算法。该算法通过引入交换突变策略，保证算法在距离r较远时萤火虫个体间仍有机会进行信息交互，从而跳出局部最优，提高全局搜索能力。该算法既保持了FA原有的简单结构，又能提高寻优精度。

选择种群中适应度函数值最小即最优的萤火虫cbest，应用交换突变策略进行操作，从而引入随机漫游，增加种群多样性，避免过早收敛。该操作过程的伪代码如下所示：

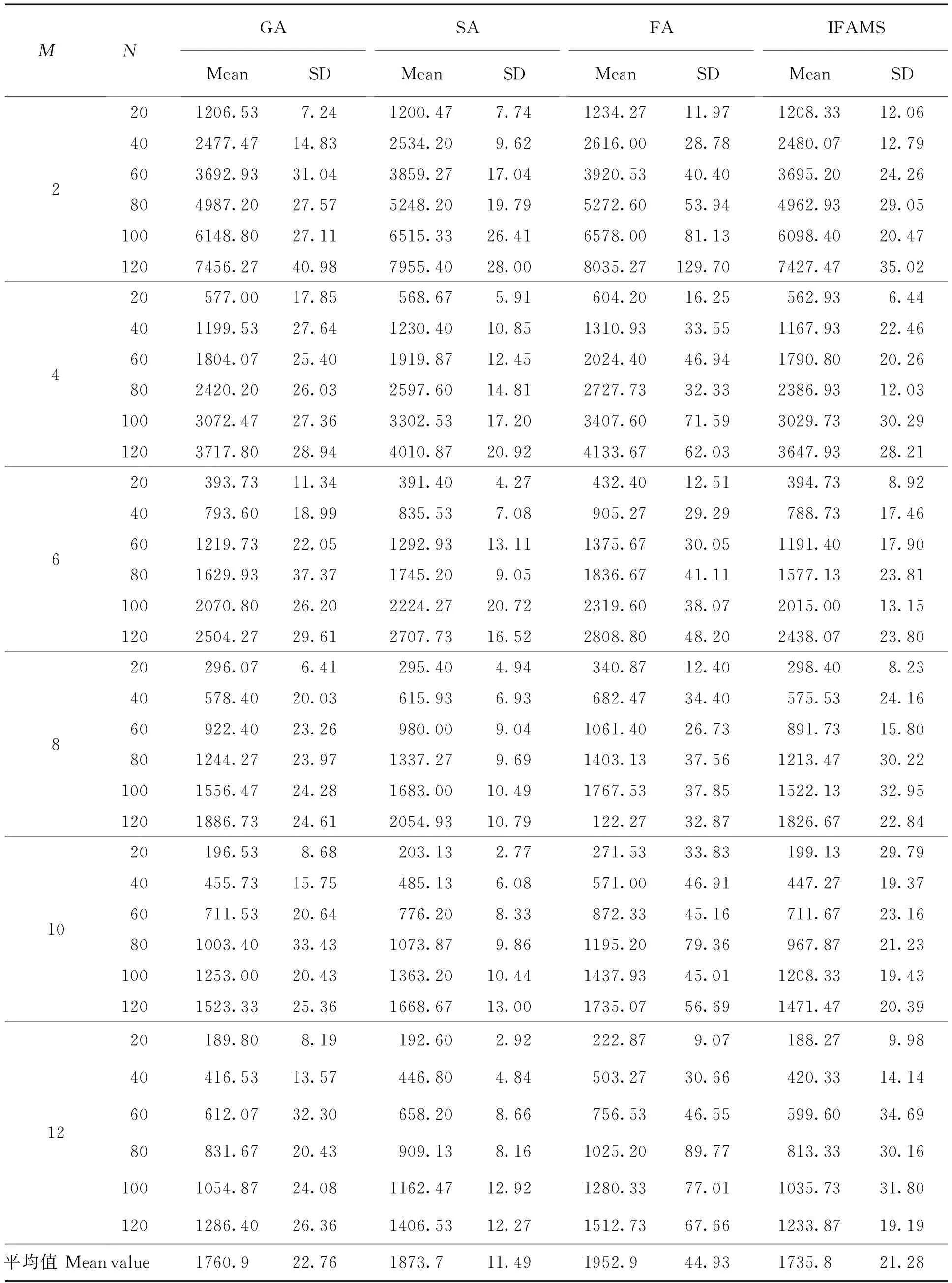
Input: cbest 从整数1到D中无放回随机均匀抽取2个值(i1和i2)作为突变位置 newbest=cbest; /*用cbest第i2维和第i1维的值分别对newbest的第i1维和第i2维进行交换*/ newbest([ i1i2])=cbest([ i2i1]); if f(newbest)

其中，cbest表示当前最优解，D代表问题的维数，f(.)表示适应度函数。

基于上述操作，改进的萤火虫算法IFAMS的完整搜索过程如下：

步骤1)采用均匀分布随机生成Np只雄性萤火虫作为初始种群{Xi|i=1，2，…，Np}；

步骤2)计算每只雄性萤火虫的发光亮度；

步骤3)如果雄性萤火虫Xj的亮度低于雄性Xi的亮度，则采用FA原来的移动策略更新雄性萤火虫位置，并更新最优解；

步骤4)执行交换突变操作；

步骤5)判断算法是否达到终止迭代的条件，若达到，则停止迭代，算法终止，否则返回并继续执行步骤3)。

2.3 IFAMS应用于含序相关设置时间的UPMSP

2.3.1 个体编码表示

设计适当的个体编码方案，能够增加IFAMS算法处理候选可行方案与萤火虫个体之间的映射效率。基于文献[1]，本研究设计了两阶段个体编码表示方案处理该问题。

1)机器分配编码

第一阶段是机器分配过程，描述了将N个任务分配给M台异构并行机，以使所有机器的最大完成时间Cmax最小的可行解，可用维数等于作业数的整数向量x表示。以10个作业、3个并行机的作业分配为例，若序列S1=[3，1，3，2，1，2，2，3，1，1]，则表示机器1分配到的作业序号为{2，5，9，10}，机器2分配到的作业序号为{4，6，7}，机器3分配到的作业序号为{1，3，8}。因此，这也要求IFAMS算法在迭代寻优过程中需要采用floor(.)函数将IFAMS中萤火虫的位置信息进行整数离散化。

2)序列调度编码

第二阶段则是确定每台机器上的作业序列。该序列可以矩阵的形式表示，矩阵的长度与机器分配向量的长度相同。因此，作业序列S2可以表示为M×N矩阵，表明每台机器上作业的执行顺序。以上文的例子为例，有

为方便求解任务完工时间，本文以校正后的处理时间矩阵APk替代两个独立阶段的时间(机器处理时间P和序相关设置时间T)进行处理。APk可以表示为上述两个阶段耗时的线性组合，数学式为：AP=θ1×T+θ2×P。

为简单起见，通常可取θ1=θ2=1，因而有：∀j=1，2，…，N，∀k=1，2，…，M；APi，j，k=Si，j，k+Pj，k，∀i=1，2，…，N。代入式(1)中，可得序相关设置时间的UPMSP问题的优化目标函数(即适应度函数)为：

2.3.2 算法应用过程

在初始化阶段，IFAMS算法首先将N个计划内的作业随机分配给M台可用的处理机器，生成由Np只雄性萤火虫个体构成的初始雄性萤火虫种群(用矩阵X表示)。每只雄性萤火虫个体对应于M×N矩阵中编码后选定的特定机器上的作业序列。外部档案A中的雌性萤火虫种群可借由雄性萤火虫种群初始化完成。

具体应用步骤如下：

步骤1)初始化。根据序相关设置时间UPMSP的数学模型和给定的机器处理时间、序相关设置时间的范围，初始化改进求偶学习萤火虫算法的各项参数。

步骤2)种群进化。IFAMS的种群进化过程如2.2节所述。

步骤3)当进化满足停止条件时，输出最优雌性萤火虫的相关信息作为近似最优调度方案。

3 仿真实验

为了验证IFAMS算法在求解序相关设置时间的UPMSP问题上的有效性，本文采用大量的测试用例进行了验证，所有实验都是通过Matlab 2020a编程实现，在8.0 G RAM 3.6 GHz CPU的Windows环境下运行。基于各个算法迭代生成过程的次数，将IFAMS算法在(Pj，k|Si，j，k|Cmax)问题中的性能表现与文献中现有的一些元启发式算法进行了比较，包括GA、SA及标准的FA算法。为了避免测试结果的随机性，每种算法重复测试15次。考虑到需要在可接受时间范围内获取可行解，因而选取最大迭代次数为1000次，Np=50，其他所有参数直接来自文献[12]。考虑到求解任务调度方案的时间相较于执行时间，比值较小，故而本文主要测试算法的求解精度，通过均值Mean和方差SD的大小来衡量。

3.1 测试用例

文献[13]的测试数据集已应用于许多相关研究中[3，7，10，12-14]。该数据集包含两个类别，即处理时间和设置时间，其数据都由离散的均匀分布U[50，100]随机生成。

本研究生成的数据集包含N个作业和M个机器，有6种情况。每种情况中的机器数量分别为2、4、6、8、10 、12，作业数量范围则分别在20、40、60、80、100、120之间。

3.2 实验结果和性能比较

根据测试用例，本研究构造得到36组算例，这些算例分别在各个算法中运行，所得结果如表2所示。其中，每种算例情况的最优值以黑色加粗标注，结果保留2位小数。由表2的数据分析可知：

表2 IFAMS算法与4种对比算法的性能比较Tab.2 Performance comparison between IFAMS algorithm and four comparison algorithms

1)从精度角度而言，IFAMS得到最优Mean值的次数远远多于FA、GA和SA，说明本文提出的IFAMS算法非常适用于求解序相关设置时间的异构并行机调度问题，表明在FA框架基础上引入交换突变策略的有效性。

2)IFAMS算法得到的结果与其他3种算法相比，能够在36个算例中的28个取得最优Mean值，并且随着算例维数的增大，IFAMS取得最优Mean值的频次逐渐增加，表明IFAMS在处理较大规模的寻优问题时其精度方面的性能优势显著。此外，在SD值方面，IFAMS也较FA取得了较大提升，其寻优稳定性仅次于SA。

图1和图2展示了机器数分别为2和10的情况下，这4个算法在不同作业数的测试用例上的平均收敛曲线。分析图1和图2可知，IFAMS表现出的收敛速度和FA相似，优于GA和SA。

4 结论

本文针对序相关设置时间UPMSP问题，提出了一种改进的求偶学习萤火虫算法IFAMS，以最小化任务完工时间为调度优化目标，求解序相关设置时间UPMSP问题。该算法引入交叉算子，在不引入额外参数的前提下，增强了萤火虫距离较远时的搜索表现，使算法能够更加充分地利用种群社会信息，增强跳出局部最优的能力，提升算法全局搜索性能。通过大量算例测试，结果表明本文所提出的调度算法在处理序相关设置时间UPMSP问题时是有效的，具有较高的收敛速度，同时精度方面相较于FA具有较大提升，相较GA和SA也有明显的优势。

边缘计算等应用场景的调度问题是调度研究的热点，但目前还未有较为统一的模型标准，未来将继续借鉴UPMSP模型，在考虑到带宽、不同网络服务提供商资费等更多约束的条件下进行研究，并提出高效算法进行求解。