典型舱段结构高频振动仿真分析方法
陈 洋,蒋 刚,梁 山,王肇喜
(上海航天精密机械研究所,上海 201600)
0 引 言
随机振动试验是防空导弹、飞机、高速列车、船舶及电力工程等领域研制过程中的一个重要环节,对于结构可靠性的验证有着至关重要的作用。数值仿真方法可以在研制阶段代替部分实物试验,节省成本,缩短研制周期。目前常用的动力学数值计算方法是建立结构的有限元模型,进行随机振动仿真分析,并结合试验数据修正仿真模型[1]。采用有限元方法可以分析随机振动环境下结构连接可靠性、疲劳寿命、应力应变等[2-4]。对于小于500 Hz 的低频振动,由于其结构的模态较为稀疏,使用有限元单元离散技术的方法能取得较为精确的结果[5]。随着结构振动频段的升高,有限元方法的单元网格需要不断加密,导致系统自由度和计算量急剧增加。高频模态分析和响应计算结果对各种不确定性因素非常敏感,结构模态密集,随机特性影响突出,因此高频振动的有限元仿真精度难以满足工程需要。
对于高频振动问题,统计能量法(statistical energy analysis,SEA)是目前主流的分析方法[6-8]。由于统计能量法从全局出发得到结构或子结构响应在空间上的统计均值,无须关注结构具体位置的响应情况,因此适用于高频振动问题[9-11]。但是仅当每个子系统的模态密度>5,并且模态重叠因子>1时,统计能量法才有效,模态稀疏的低频段往往无法满足该要求[10-11]。
对于包含低、中、高频的宽频随机振动问题,单独采用有限元(finite element,FE)或者统计能量分析(statistical energy analysis,SEA)方法均无法获得精确的结果。为了解决现有仿真方法无法满足包含从低频到高频的宽频域随机振动问题,有研究人员提出一种思路,即根据结构模态分析的结果,将系统划分为确定性子系统和统计性子系统两类,分别采用有限元建模和统计能量法建模,并将两种子系统耦合起来[12-13]。FE-SEA 混合方法结合了有限元方法和统计能量分析方法各自在低频与高频段的优势,有望成为连接低频与高频问题的桥梁,实现结构全频域的宽频随机振动高效、高精度仿真分析[14-15]。
防空导弹、运载火箭等航天器服役过程中,低频响应和高频振动响应均对机电系统稳定性、结构可靠性有显著影响[16],但目前仿真还存在困难。为突破防空导弹系统随机振动的高频耦合建模难题,本文以典型舱体结构为研究对象,采用基于波动耦合理论的FE-SEA分析方法,确定结构子系统划分原则,研究舱体结构在5~2 000 Hz频率范围内典型随机振动条件下的响应,通过实物试验修正并验证仿真结果,以期为防空导弹舱体结构随机振动试验建立一套有效的仿真分析模型。
1 FE-SEA混合分析方法
1.1 基于波动耦合的FE-SEA基本理论
基于波动耦合的混合建模方法,其基本原理为,基于能量守恒推导各SEA 子系统能量响应方程,并从统计的角度建立FE子系统的位移响应与SEA子系统的能量响应之间的关系,从而达到耦合FE 子系统和SEA子系统的目的。
一般而言,对于确定性子系统其总体动力学方程表示为
式中:N为SEA 子系统的总数目;u为FE 子系统的总自由度数;fre(k)为FE 子系统边界处的混响场载荷(上标k表示第k个SEA 子系统);fex为作用于FE 子系统的外部激励;Dtou为FE子系统总体动刚度。
Dtou可以表示为
式中:Dd为在边界处FE 子系统的动刚度;为第k个SEA子系统对于FE子系统的直接动刚度。
通过式(2)可以求得FE子系统的自由度数为
当SEA 子系统中有足够参数为不确定性时,耦合边界上的混响力则可由扩散场互易表示为
式中:为混响力的互谱矩阵;Ek为第k个SEA子系统能量响应;Im{ }为取虚部;nk为第k个SEA 子系统模态密度;ω为圆频率。
式(4)建立了SEA 子系统能量响应与SEA 子系统耦合边界上作用于FE 子系统载荷之间的关系,提供了计算的方法。通过式(3)与式(4)可得到FE子系统自由度u的互谱矩阵如下:
式中:上标“H”为“Hermitian转置”。
同时,由式(1)—式(5)可以推导得到混合FESEA系统的功率平衡方程如下:
式中:ηj,k为子系统j和子系统k的耦合损耗因子;ηj为SEA 子系统与FE 子系统j之间的阻尼损耗因子;Pj为由外界输入SEA 子系统j中的功率;为第j个SEA子系统接收的输入功率,其来源是作用在FE 子系统上的外部激励;Sff为施加到FE 子系统的载荷力的互谱矩阵。
在建立FE-SEA 混合后,SEA 子系统的平均振动能量可以通过式(6)求解得到。根据SEA 子系统能量响应与FE子系统荷载之间的关系,求解式(5)得到FE子系统振动速度、加速度。
1.2 基于波动理论的FE-SEA混合方法分析
基于波动理论的FE-SEA 混合方法的基本流程如图1 所示。具体分析过程如下:① 划分系统;②获取边界连接处的动刚度阵;③ 分析确定性子系统的参数;④ 分析与随机子系统相关的参数;⑤ 随机子系统响应的求解;⑥ 确定性子系统响应的求解;⑦ 重复步骤②~⑥,计算下一个频段响应的平均集合。
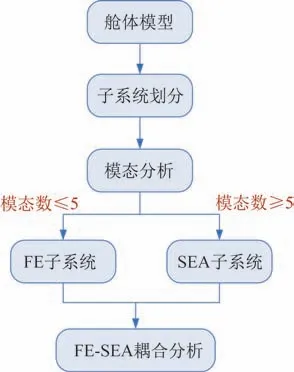
图1 FE-SEA混合方法分析流程Fig.1 Analysis flow chart of the FE-SEA method
2 舱体结构随机振动试验的FE-SEA仿真分析
2.1 建立振动试验系统模型
为了反映导弹舱体结构在随机振动试验中真实的响应情况,建立振动台动圈、滑台以及舱体结构的联合模型,如图2 所示。已知振动台及滑台部件在500~2 000 Hz 的模态数<5,因此仿真分析中振动台与滑台都采用有限元模型。
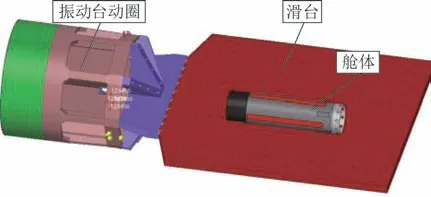
图2 振动台动圈、滑台以及舱体结构的联合模型Fig.2 Joint model combined by moving coil of vibration table,sliding table and cabin
振动台动圈、滑台与舱体之间通过螺栓连接,在HyperMesh 软件中通过梁单元和节点耦合方式模拟螺栓功能实现3个部分的连接。振动台动圈和滑台由AZ31镁合金制成,舱体为6061铝合金结构件,各部分的材料参数见表1。
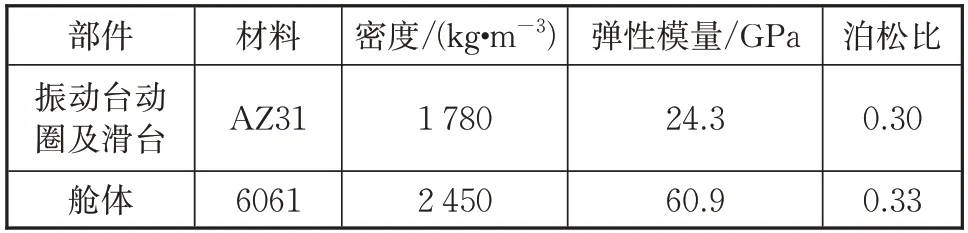
表1 振动台动圈、滑台和舱体的材料参数Tab.1 Material parameters of moving coil of vibration table,sliding and cabin
2.2 舱体结构的子系统划分
仿真分析工作中对舱体结构进行了简化,忽略了舱体上的细小附件以及内部设备,填补对计算分析结果影响不大的孔洞,对舱体结构存在的其他影响计算精度的部分进行简化与修正处理,最终得到简化过后的舱体结构模型,如图3所示。舱体结构主要分为5个部件:前圈、后圈、中间半圆柱板1、半圆柱板2及4个加强板,4个加强版厚度分别为5.5、5.5、1.5和8 mm。

图3 舱体结构模型Fig.3 Model of cabin structure
对舱体结构划分有限元网格并进行模态分析,计算频率500~2 000 Hz,各个部件所对应的模态数如图4所示。
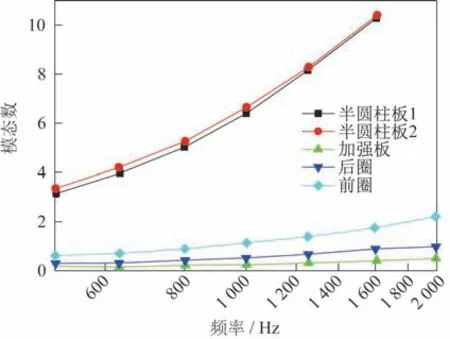
图4 舱体各部件对应模态数Fig.4 Model order of each component
由图4 可见,500~2 000 Hz 时两个半圆柱板所对应的模态数均>3,800 Hz 左右时均>5,因此这两个部分采用统计能量分析模型精度是足够的。剩余的前圈、后圈以及加强板部分对应的模态数较小,无法达到使用统计能量模型的要求,因此在分析中应当采用有限元模型。最终舱体子系统划分方式及各部分能量传递关系如图5 所示,其中红色箭头为SEA 子系统之间的能量传递,蓝色箭头为FE 子系统和SEA 子系统之间的能量传递。
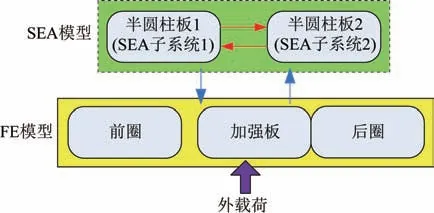
图5 舱体有限元-统计能量子系统划分及能量传递方式Fig.5 Subsystem division and energy transfer path on cabin structure
2.3 振动台 夹具 舱体结构FE-SEA 分析模型建立
在舱体随机振动试验仿真分析中,将振动台动圈和滑台作为虚拟振动试验系统,建立有限元模型,将舱体结构通过螺栓连接安装在滑台上,如图6 所示。通过虚拟振动试验系统对舱体施加激励,整个过程类似于实物试验。所建立的振动台-夹具-舱体结构FE-SEA 分析模型及各部分能量传递方式如图7 所示。FE-SEA 分析过程采用VA one 软件进行计算。在航空航天领域,铝板的内损耗因子约为0.02,因此采用该值作为内损耗因子的大小。耦合损耗因子表征了两个子系统之间的耦合程度,决定两个子系统之间能量传输的能力,耦合损耗因子由软件计算得到。

图6 振动台-夹具-舱体结构FE-SEA模型Fig.6 FE-SEA model of the joint model
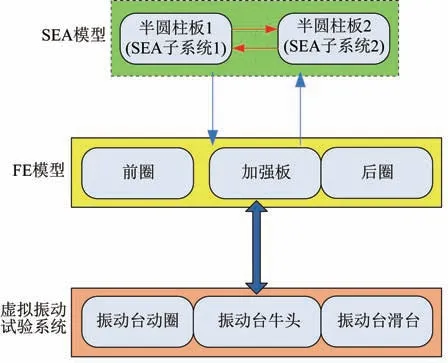
图7 联合模型有限元-统计能量子系统划分及能量传递方式Fig.7 Subsystem division and energy transfer path on a joint model
2.4 随机振动试验仿真计算结果
研究舱体结构在振动台提供随机振动条件时的响应,选择一个典型的随机激励载荷,见表2。其功率谱密度值随着频率变化的曲线如图8所示。

表2 给定随机激励载荷Tab.2 Random excitation load spectrum
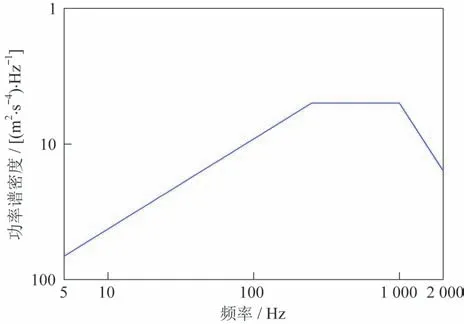
图8 随机振动载荷Fig.8 Curve of random excitation load spectrum
计算获得舱体各部件的振动加速度响应如图9所示,模型各部分之间能量传递关系如图10所示。由图9 可见,半圆柱板2 的加速度响应略大于半圆柱板1 的响应,说明其响应大小由于各板连接之间存在耗散而不同,能量由半圆柱板2 传至半圆柱板1 时有部分能量耗散。由图10 可见半圆柱板1 的能量大部分由半圆柱板2 传来,少部分能量由动圈通过有限元部分传来。

图9 振动响应曲线Fig.9 Curve of vibration response
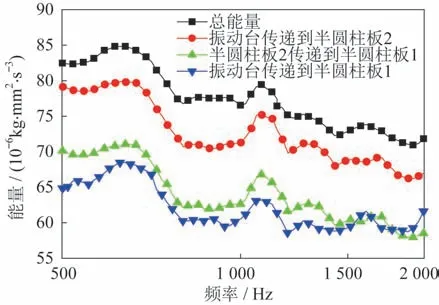
图10 能量传递曲线Fig.10 Curve of energy transfer
2.5 试验结果及仿实一致性分析
根据2.4 节中模拟试验方案设计随机振动试验方案。如图11(a)所示,将某型号电子舱通过夹具以及转接工装安装于振动台台面,按照如图11(b)所示方式布置振动传感器测点,以CH1、CH2、CH3、CH4 为控制点进行随机振动试验,监测点A1~A4 和A5~A8分别监测半圆板1 和半圆板2 上的振动响应。试验控制曲线及舱体响应结果如图12所示。

图11 舱体随机振动试验Fig.11 Random vibration test of cabin

图12 舱体随机振动试验数据Fig.12 Random vibration test data of cabin
根据所划分的舱体统计能量子系统,将两个子系统上的测点响应平均处理,按1/12倍频程带宽计算各频段中的振动响应均方根(root mean square,RMS)值,试验与仿真结果的对比如图13 所示,仿真数据与试验数据吻合较好。
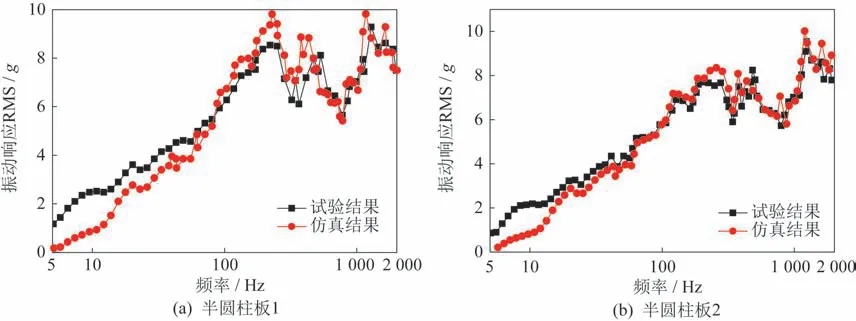
图13 仿真与试验的振动响应RMS数据对比Fig.13 Comparison between simulation and test of vibratory response RMS
计算得到子系统1 在500~2 000 Hz 的试验结果,总振动响应RMS 值为15.4g,仿真结果总振动响应RMS 值为18.7g,子系统1 振动响应有效值误差约为1.6 dB。计算得到子系统2在500~2 000 Hz的试验结果,总振动响应RMS值为17.3g,仿真结果总振动响应RMS 值为22.1g,子系统2 振动响应有效值误差约为2.1 dB。两个子系统振动响应有效值误差均小于3 dB,反映出导弹模拟舱体的高频随机响应仿真结果与试验结果具有较好的一致性。
3 结束语
本文完成了典型舱体结构的统计能量分析建模方法,通过开展频率特性分析,将舱体结构上模态数>5 的部分作为统计能量分析子系统,建立舱体结构的统计能量分析模型;讨论了基于波动理论的FE-SEA 混合方法分析过程,基于有限元-统计能量分析对典型舱体结构进行随机振动试验仿真分析,得到舱体部件的加速度响应。仿真数据与实物试验数据对比,振动响应有效值误差均<3 dB,说明采用FESEA 混合方法的仿真结果与试验结果具有较好的一致性。

