超声速风洞带舵机状态全尺寸舵颤振亚临界试验

王 珏，王誉超，季 辰

（中国航天空气动力技术研究院，北京 100074）

0 引 言

战斗机、导弹等高速飞行器全动舵的颤振是其气动弹性设计中需要关注的重要问题之一。采用缩比模型开展风洞颤振试验是研究飞行器舵翼面经典颤振的重要方法。试验中，按照气动相似和结构动力学相似的原则，设计一定频率和质量刚度特性的缩比模型模拟真实结构的结构动力学特性和外形［1-8］，通过风洞颤振试验获得舵翼面的经典颤振特性。该方法在型号设计中得到了广泛的应用［9-12］，但仍有不足，主要体现在两方面：① 采用缩比模型难以完全模拟舵结构的真实动力学特性，如舵面支撑系统及舵机系统等效刚度的模拟精度、舵支撑及舵机系统间隙等结构的非线性效应问题；② 缩比模型难以考察舵机伺服控制等其他复杂因素的影响。因此，真实全动舵的颤振问题不仅是经典颤振问题，还受其他更复杂因素的影响，需要进一步发展全动舵颤振和气动弹性评估技术。

为了克服缩比模型风洞颤振试验的上述缺点，近年来发展了一种颤振试验新方法，即采用真实全动舵和舵系统结构，通过计算的方法解算出非定常气动力，并使用激振器或其他方式来模拟气动力输入［13-14］，进行地面颤振试验来研究舵面气动弹性特性。如俄罗斯中央空气流体动力研究院（TsAGI）提出的机电方法（electromechanical method，EMM）、ZONA 公司提出的干风洞（dry wind-tunnel，DWT）颤振试验系统［13］等均基于该理念。该方法在试验中需要解算气动力并输入到激振器激励，过程较为复杂，因此在工程实践中也有诸多问题需要解决。

随着我国中大型高速风洞的建立，小尺寸舵面的实物带舵机风洞气动弹性试验成为可能。该方法既能真实地反映舵面以及连接部分的结构动力学特性，又能模拟舵面主要气动特征，还可以在试验中引入舵机的伺服控制，是舵面气动弹性研究的重要发展方向，但目前尚未见到国内相关研究的报道。该方法有两个问题需要解决：① 舵面舵系统在风洞中安装支撑的问题；② 由于风洞动压范围的限制，往往不能在风洞动压范围内获得颤振点。针对后者，目前有诸多亚临界颤振边界预测方法可以应用，如阻尼外推法、颤振边界函数法、包线函数法、自回归滑动平均（autoregressive moving average，ARMA）方法、NG（nissim and gilyard）方法、Peak-Hold法等［15-16］。

为了实现全尺寸舵的带舵机风洞颤振试验，本文基于FD-12 风洞设计全尺寸舵气动弹性的试验机构，可在风洞试验段中实现全尺寸舵和舵机的安装，且具有舵面流场冲击保护功能。本文采用固定马赫数连续变动压的风洞运行方式，对某带舵机全动舵实物进行颤振试验，试验固定马赫数Ma为1.5，未到颤振动压，采用3 种亚临界颤振边界预测方法，对全尺寸舵带舵机状态下的颤振边界进行预测和评估，验证亚临界颤振方法在超声速风洞试验中的可行性。

1 试验装置

舵面气动弹性试验装置可以将真实舵机连同舵机舱支撑在风洞试验段，如图1 所示。整个机构安装在风洞试验段侧窗位置处，主要由滑动平台、底座和舵机舱组成。安装全动舵和舵机的舵机舱固定在滑动平台上，该平台安装在底座上，由电机丝杠驱动。

舵面模型和舵机舱的安装关系如图2所示。舵面模型位于舵机舱侧面，直接安装在舵机舱内的舵机上。整个试验过程中，仅当风洞流场稳定后，驱动滑动平台将舵面模型推入流场范围内，其余时刻舵面模型均位于风洞流场范围外，以此减少模型在流场建立过程中受到的冲击，保护试验模型和机构。

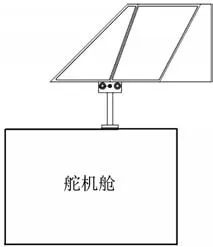
图2 舵面与舵机舱安装示意图Fig.2 Installation diagram of rudder model and steering gear cabin

试验时，通过控制电机的运行使机构在准备状态和试验状态中切换。准备状态（流场稳定前）插入机构将模型推出，使模型处在风洞流场范围外的驻室中。当流场稳定后，电机开始运行，使载物台和试验模型沿滑轨向风洞流场方向运动，最终到达试验需要的位置，即进入试验状态（见图1）。完成试验后，电机反向运行使模型移出风洞流场范围，机构回到准备状态。

2 舵面模型动力学特性

舵面模型为直角梯形，量纲为1的舵面尺寸：展长为0.48，根弦长为1，尖弦长为0.52，舵轴长度为0.20，距根部前端为0.38。舵面前缘A处（距舵轴0.27）和后缘B处（距舵轴0.52）分别安装加速度传感器，测量振动响应。舵面实物如图3所示。

图3 试验用舵面实物Fig.3 Real rudder model for test use

由模态试验结果得知，全尺寸舵带舵机状态一阶频率为24.6 Hz，阻尼比为1.4%；二阶频率为63.7 Hz，阻尼比为2.5%，舵面最大位移归一化振型如图4 所示。地面振动试验（ground vibration test，GVT）得到的舵面结构动力学特性与安装在导弹上的真实舵面一致。

图4 舵面最大位移归一化振型Fig.4 Maximum displacement normalized mode shapes of the rudder model

3 试验设备

3.1 风洞设备

试验在FD-12 风洞中开展。该风洞是一座暂冲式亚跨超三声速风洞，Ma在0.4～4.0 之间，试验段横截面尺寸1.2 m×1.2 m，风洞外形如图5所示。

图5 FD-12风洞外形Fig.5 FD-12 wind tunnel

3.2 采集设备

试验采用INV3060A 网络式数据采集系统。该系统共有16 通道、24 位，每通道独立进行模拟信号到数字信号转换（analog to digitalg，AD），并行无时差，每通道最高采样率为51.2 kHz，具有交流电压和直流电压，内置电路压电（internal circuits piezoelectric，ICP）输入模式。试验中采用该系统采集舵面模型上的加速度信号。

3.3 传感器

试验采用加速度传感器进行测量。图3 中舵面前缘A处采用PCB 352A91 高温加速度计（7#加速度计），后缘B处采用Endevco 2250 加速度计（8#加速度计），如图6 所示。

图6 试验用加速度传感器Fig.6 Accelerometers for test use

4 风洞颤振试验

4.1 试验概况

试验采用图2 所示安装模式，通过舵机将舵面安装在舵机舱上，并将舵机舱安装在气动弹性试验机构上。舵面在试验段流场中伸出的情况如图7所示。试验采用固定马赫数连续变速压的方式，通过舵面加速度计测量舵面加速度响应。有效吹风试验数据如图8所示，图中分别为马赫数波动曲线、动压q变化曲线、7#（前缘A点）和8#（后缘B点）加速度计的振动响应曲线。由图8 可见，风洞在流场稳定后实现了动压的连续增压，变动压试验时平均Ma为1.44。

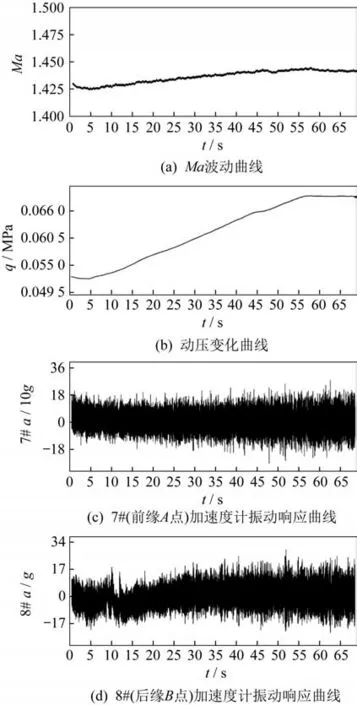
图8 吹风试验数据Fig.8 Wind tunnel test data

由7#和8#加速度计时域响应情况可见，在试验动压范围内舵面并未发生颤振。通过时频域分析方法，对7#加速度计响应数据进行短时快速傅里叶变换分析，获得数据的时频域曲线如图9 所示。由图9 可见，随着动压增加一阶、二阶模态的频率，耦合趋势明显。结合地面振动试验结果分析，这两个频率的模态分别对应模型的一阶和二阶振动模态。

图9 7#加速度计时频谱Fig.9 7# Accelerometer spectrum

4.2 颤振边界预测

为了获得全动舵的颤振边界，需要分析亚临界试验数据，对颤振边界进行预测。文献［16］介绍了诸多颤振边界预测方法，从风洞颤振试验的角度来看，Houbolt-Rainey 颤振边界预测方法、Peak-Hold 颤振边界预测方法和Zimmerman-Weissenburger 颤振边界函数法较为实用，且鲁棒性较好。本文采用上述3 种方法对舵面的颤振边界进行预测和分析，获得该全动舵的颤振动压。

4.2.1 Houbolt-Rainey方法

Houbolt 和Rainey 于1958 年提出Houbolt-Rainey颤振边界预测方法，该方法适用于飞行颤振试验和风洞颤振试验，模型可以采用正弦激励和随机紊流激励。对于仅有紊流激励的情况，振动响应幅值a的倒数为

式中：Q为广义力；A为广义气动力，是马赫数、减缩频率的函数；V为来流速度；ρ为流体密度；下标f、t 分别代表颤振、紊流。

Houbolt-Rainey 方法认为，接近颤振点时，结构振动响应趋近于无穷大，即随着来流动压增加接近颤振动压，1/|a|值不断趋于0。通过得到响应幅值倒数，并随着动压的变化趋势推测出颤振临界点。该方法理论模型较为简单，但从多年来国外风洞试验以及飞行颤振试验应用情况来看，该方法适用性较高，尤其是对风洞颤振试验中的颤振动压辨识。

对本试验吹风情况下的数据进行分析，得到1/|a|随风洞动压的变化趋势，如图10所示。采用最小二乘直线拟合的图10曲线，外推到纵坐标为零的横坐标即为颤振临界动压，即采用Houbolt-Rainey 方法得到颤振动压为0.070 MPa。

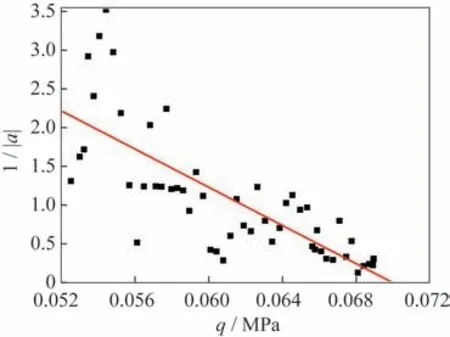
图10 Houbolt-Rainey方法颤振边界预测Fig.10 Houbolt-Rainey flutter boundary prediction

4.2.2 Peak-Hold方法

Zeng 等［13］于1975 年提出Peak-Hold 法，这是一种基于工程经验的方法，其原理与Houbolt-Rainey 方法类似。与Houbolt-Rainey 方法不同的是，在实际数据处理时，该方法运用了Peak-Hold 思想，即在某一小时间段内，取该段时间下所有幅值谱的最大值作为该段的峰值，称之为Peak-Hold谱峰值，即

通过该谱峰值的倒数1/|aPeak-Hold|随动压变化进行插值，过零点即为颤振边界点。该方法是目前NASA Langley 研究中心跨声速动力学风洞（transonic dynamics tunnel，TDT）气动弹性风洞颤振试验的亚临界边界颤振预测标准方法，常用于高速风洞颤振试验。

1/|aPeak-Hold|随风洞动压的变化趋势如图11所示，图中每一点为一定区间内的Peak-Hold 谱峰值倒数。由于采用Peak-Hold 思想，数据点为一定时间区间内的谱峰值，因此数据量较图10降低。采用最小二乘直线拟合图11数据可以外插得到颤振临界动压，即通过Peak-Hold方法得到颤振动压为0.072 MPa。

图11 Peak-Hold方法颤振边界预测Fig.11 Peak-Hold flutter boundary prediction

4.2.3 Zimmerman-Weissenburger方法

Zimmerman-Weissenburger 颤振边界函数［14］基于2 自由度颤振特征方程推导得到。颤振边界函数F可以用颤振相关的模态频率ω和模态阻尼β的函数表示出，其表达式为

采用函数拟合颤振边界函数随动压的变化曲线F（q）可以得到当F（q）=0 时的颤振临界参数。该方法常用于2 自由度耦合颤振的情况，适用于低速风洞、高速风洞颤振试验和飞行试验，并且可用于预测距颤振临界点较远的亚临界试验情况下的颤振边界。

对试验数据进行分段分析，辨识出每段数据的一、二阶模态频率ω1、ω2和阻尼β1、β2并带入。颤振试验中一阶、二阶频率随动压的变化如图12所示。计算得到的颤振边界函数随动压变化情况如图13 所示。采用最小二乘线性插值的方法外插可预测出颤振边界为0.073 MPa。

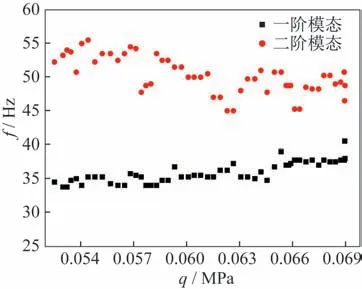
图12 颤振试验中随动压的频率变化Fig.12 Frequency variation with dynamic pressure in flutter test

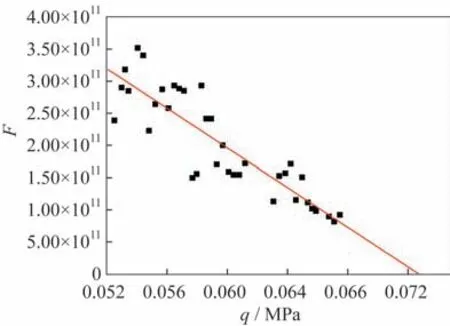
图13 Zimmerman-Weissenburger方法颤振边界预测Fig.13 Zimmerman-Weissenburger flutter boundary prediction

4.3 颤振临界动压

利用风洞试验亚临界数据得到的颤振临界动压见表1，其中采用Houbolt-Rainey方法预测得到颤振动压为0.070 MPa，采用Peak-Hold方法得到颤振动压为0.072 MPa，采用Zimmerman-Weissenburger 方法得到颤振动压为0.073 MPa，3种方法预测得到的颤振动压最大相差约为4.1%。

表1 颤振临界动压Tab.1 Flutter critical pressure

5 结束语

1） 本文建立基于FD-12 亚跨超声速风洞的全尺寸舵气动弹性试验机构，开展带舵机全尺寸舵固定马赫数连续变速压超声速风洞颤振试验，试验Ma为1.5（实测Ma为1.44）。试验检验了设计的气动弹性试验机构，验证了该机构能够一定程度减小流场对试验模型的冲击，可用于开展实物舵带舵机气动弹性风洞试验研究。

2） 试验采用固定马赫数连续变速压的开车方式，采用亚临界颤振边界辨识方法，在吹风中未到达颤振临界点的状况下，采用Houbolt-Rainey、Peak-Hold、Zimmerman-Weissenburger 方法预测得到颤振动压分别为0.070、0.072、0.073 MPa，三者基本一致。

3） 试验表明，对于目前舵面尺寸较小的空空导弹、地空导弹等导弹舵翼面，可以采用全尺寸舵面和真实舵机舱在风洞中开展舵面颤振试验。在真实动压低于实际飞行动压的情况下，通过亚临界参数辨识的方法获得舵面的颤振动压。该试验方法可应用于型号研制的颤振校验中，并为后续带伺服控制舵面气动弹性试验打下基础。