随动推力作用下细长体结构振动模态特性及稳定性分析

李海东，沈奕哲，侯凯宇，夏 鹏，刘陆广，管耀耀

（1.上海机电工程研究所，上海 201109；2.上海航天技术研究院，上海 201109；3.上海航天精密机械研究所，上海 201600）

0 引 言

新一代飞行器向超高速、大攻角、高机动、大长细比和轻量化方向发展，其结构特性发生显著改变，更加柔性，受到扰动后更易产生弹性变形［1］。传统飞行器各系统孤立设计、分段验证的方法已经不能适应其发展的需要［2］。尤其是飞行器采用的固体火箭发动机的输出推力矢量方向始终与结构的尾端相切，飞行过程中随着细长体飞行器振动变形，轴线发生变形，推力方向也随着振动改变。这种随着结构振动改变作用方向的力称为随动推力。

早在20 世纪60 年代，细长体导弹的弹性效应问题就开始受到学者关注，更是当前航天工程中的热点问题。Beal 等［3］在1965 年研究理想化为均匀自由梁的弹性导弹在随动推力影响下的动力学稳定性问题，并考虑脉动推力和简单的方向反馈控制系统的影响。Mladenov 等［4］研究铰接自由梁结构的振动稳定性问题。Joshi 等［5］研究大推力对弹体结构稳定性的影响。宋健［6］研究空气阻力和推力同时作用时，火箭横向振动的模态特性，并对火箭模态频率降低的原因进行解释。许赟等［7］将弹箭飞行器简化为非均匀梁模型，采用有限元法分析随动力作用下弹箭结构的模态特性和稳定性，研究弹箭结构的模态特性（模态频率和模态振型）及稳定性受随动力的影响。罗梦翔等［8］假设推力阻力平衡，研究推力以及轴向运动共同作用下弹体结构的稳定性。Esbati 等［9］研究三级运载火箭在随动推力作用下的模态特性以及稳定性。Ahmadia 等［10］对随动推力作用下两端自由的铰接梁动力学稳定性的变化展开研究。滕兆春等［11］建立了梁在轴向载荷作用下过屈曲横向自由振动的精确模型，获得线性振动的响应，发现轴向力对过屈曲前后梁的各阶固有频率均有影响。Pourtakdoust 等［12］研究推力对柔性导弹弯曲特性的影响，发现质量减小增加导弹振动频率，推力作用减小振动频率。

关于随动推力是否可以作为随动载荷加载在结构上，并影响结构的振动特性及动力学稳定性一直存在争议［1，13］。Sugiyama 等［14-16］开展固体火箭发动机推力作用于悬臂梁自由端切线的相关试验，验证了工程应用中考虑随动推力的必要性。但是关于随动推力是怎么影响导弹细长体结构模态特性和稳定性的具体问题，前文学者多数只考虑随动推力轴向分量的影响，未考虑随动推力横向分量的影响，部分引入随动推力横向分量仅进行定性分析，对横向分量对导弹模态特性和稳定性的影响未进行定量对比分析。

本文将开展随动推力作用下细长体结构振动特性数值仿真研究，对引入随动推力横向分量后细长体结构模态特性、稳定性进行分析，并与仅考虑随动推力轴向分量作用时的情况进行对比，定量分析有无随动推力横向分量对模态特性的影响。

1 结构动力学模型

随动推力作用下的细长体结构示意如图1 所示。图中：F为随动推力；Ff为随动推力横向分量；FN为随动推力轴向分量；w为横向位移；x为细长体结构轴向以及其运动方向坐标。将该细长体结构划分为n个梁单元，考察其中长为l、密度为ρ、截面积为A、抗弯刚度为EI的第e个梁单元。

图1 随动推力作用下细长体Fig.1 The diagram of the slender body under follower thrust

该梁单元动能T表达式为

设梁单元两端节点分别为i、j，梁单元节点位移w(e)是两端节点的挠度和转角，即

式中：wi、wj为梁单元两端节点的横向位移；θi、θj为梁单元两端节点的转角，θi、θj为小量。

梁单元的横向位移为

将式（3）代入式（1），得

式中：M(e)为梁单元质量矩阵。

由于引入随动推力，该梁单元势能V表示为

式中，P(x)为随动推力轴向分量在梁轴向的分布函数。

将式（3）、式（8）代入式（7），得

式中：K(e)s为梁单元结构刚度矩阵；K(e)p为梁单元初应力矩阵。

由式（11）可见，梁单元的初应力矩阵由随动推力轴向分量引入。关于随动推力的影响，均只考虑了随动推力的轴向分量FN，但随动推力在横向也存在分量Ff，如图2所示。

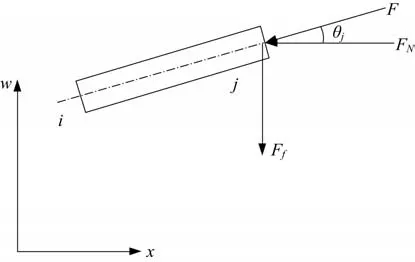
图2 随动推力分解Fig.2 The decomposition of follower thrust

由图2可得

Ff作用在最后一个单元的j节点上，因此，广义力f(e)为

式中，K(e)f为随动推力横向分量引入的刚度矩阵。

应用拉格朗日方程建立振动方程为

式中：qj为广义坐标；f(e)j为对应于广义坐标的广义力函数。

将式（1）、式（7）带入式（16）得

由式（13）、式（16）、式（17）可得随动推力作用下梁单元的横向运动方程为

整理得

式（20）中，随动推力横向分量作为刚度项引入。根据各个单元之间的变形协调条件和平衡条件，得到整个细长体结构的质量矩阵M，刚度矩阵K，从而得到整个细长体结构的横向振动方程为

解式（21）的广义特征值，得到随动推力作用下细长体结构的模态特性。

2 模态特性及稳定性研究

对于不同的发动机随动推力F，求解其作用下细长体结构的横向振动方程，得到一系列广义特征值。如果某个特征值出现了正实部，且此时某阶特征频率f降为0 或者某两阶频率f1、f2重合，称此时的随动推力为临界推力，记为Fcr。

设计一个1 200 mm×30 mm×9 mm 的细长体铝杆，对随动推力F作用下该细长体结构稳定性进行分析，结果见表1。由表1 中可见，不考虑随动推力横向分量情况下，细长体铝棒的不稳定屈曲问题是经典的压杆稳定问题，此时细长体系统的屈曲临界轴向力为180 N；考虑随动推力横向分量情况下，细长体铝棒的不稳定问题是动力学失稳问题，此时细长体系统的临界推力Fcr为1 620 N。在随动推力横向分量作用下，该细长体系统的动力学失稳临界值明显高于静态屈曲的临界值。

表1 细长体系统不同情况下的临界力值Tab.1 The critical force of the slender body structure

该细长体系统不考虑随动推力横向分量、考虑随动推力横向分量情况下的频率与推力关系如图3和图4 所示。不考虑随动推力横向分量情况的屈曲问题中，推力作用方向始终沿着未变形前的细长体轴线。由图3 可见，这种情况下模态频率f1、f2只会依次单调下降至0，不会出现系统频率相互接近、模态耦合的现象。由图4 可见，在考虑随动推力横向分量情况下，随着随动推力逐渐增大，细长体系统1阶频率f1逐渐上升，2 阶频率f2逐渐下降，两者呈相互靠近的趋势，在临界点上1、2 阶频率重合，证实随着细长体弯曲振动，随动推力作为随动载荷始终作用于细长体自由端切线方向，其横向分量引起了模态间的刚度耦合。

图3 细长体系统频率与推力关系曲线（不考虑随动推力横向分量）Fig.3 Frequency-thrust curve of the slender body （no thrust transverse component）

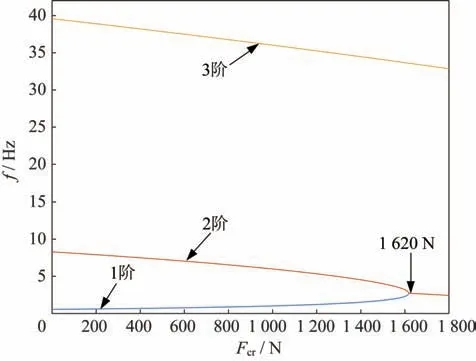
图4 细长体系统频率曲线（考虑随动推力横向分量）Fig.4 Frequency-thrust curve of slender body （considering thrust transverse component）

3 结束语

1） 随动推力轴向分量为保守力，引起细长体轴向刚度的削弱；细长体弯曲振动引起的随动推力横向分量为非保守力，引起系统模态间的耦合，容易产生动力学失稳。

2） 对于一个给定的细长体结构，在随动推力作用下，系统的动力学失稳临界值高于静态屈曲的临界值；在动力学失稳的临界点上，细长体系统的1、2阶频率重频。