厚薄通用四边形平板壳元在薄壁结构加筋布局优化中的应用

王 谦，丁晓红，张 横

（上海理工大学 机械工程学院，上海 200093）

0 引 言

舵面作为弹体的重要部件，是飞行器主要承力部件之一，具有轻质、高承载的设计要求［1］。舵面结构由薄壁板壳结构组成，单纯薄壁板壳结构的刚度、强度、振动等力学性能不佳，在实际应用中一般采用加筋结构形式。布置加强筋能够以较小的质量增加为代价，大幅提高板壳结构的静动态性能。因此，如何布局加强筋成为了加筋设计中的重点问题。

近年来，研究人员将结构拓扑优化引入舵面结构加强筋分布的设计中，提升了舵面结构的各项性能［2-4］。但是基于变密度法（density method）寻求最优材料布局进而间接确定加强筋位置的方法需要特殊的后处理手段，才能判定加强筋的实际位置、走向、厚度等，但后处理过程存在一定的主观性，会影响优化设计结果的最优性。丁晓红等［5-6］提出了一种启发式几何显式加筋拓扑优化方法“自适应成长法（adaptive growth method）”，该方法基于自然界分枝系统成长、分歧与退化机理发展而来。相较变密度法等几何隐式方法，自适应成长法直接以加强筋截面几何参数作优化设计变量，具有优化效率高、优化结果清晰、可制造性强等优点，近年来被广泛运用于各类板壳结构加筋静动态优化设计中。

自适应成长方法通过有限元方法进行结构分析，在迭代中以筋板截面参数变化表示“成长”和“退化”。季学荣［7］利用自适应成长法对汽车发动机罩板加筋布局进行了设计。侯剑云［8］同样受自然界生物自适应成长机理启发，提出基于连续阶跃参考应力的软杀法（soft kill optimization，SKO）。这两项研究的结构分析部分利用商业有限元分析软件，采用差分法计算单元灵敏度，因此，计算精度受到限制且计算效率较低；Shen 等［9-10］基于自适应成长法提出了3D 箱型结构的刚度、阻尼协同优化方法，结构分析部分利用Long 等［11］提出的基于广义协调理论的平板型矩形壳元GCR24 处理的，该单元由平面薄膜元GR12 和薄板弯曲元GPL-R12 单元耦合构建。GCR24 单元用于几何显式板壳加筋拓扑优化时具有列式简单、计算效率高的优势，同时在筋板厚度变化过程中避免了剪切闭锁问题，但GCR24 单元是矩形单元，不能满足舵面等复杂结构的有限元分析对网格灵活性的需求。

综上所述，利用自适应成长法对舵面结构的加筋布局进行拓扑优化，构建一种厚薄通用、高准确度的四边形平板壳元十分必要。本文通过耦合GQ12膜元和MITC4 板元构造了四边形平板壳元并构建基结构，随后引入自适应成长法对舵面结构进行加筋布局拓扑优化，以此实现结构的轻量化设计。

1 GQ12 膜元与MITC4 板元耦合的四边形平板壳元

1.1 具有旋转自由度的四边形膜元GQ12

为克服低阶位移型单元计算精度差的问题，Long等［12-13］采用广义协调条件构造了具有旋转自由度的四边形膜元GQ12，该单元列式简单，能通过任意四边形分片检验收敛单元，计算精度较高。GQ12引入刚体转角作为单元节点的旋转自由度，每个节点有两个线自由度和一个平面内转角自由度，每个节点的自由度为

式中：ui、vi为节点线位移分量；θi为节点附加平面内转角位移分量。

GQ12膜元的位移场由两个部分组成：

式中：u0=[u0v0]T，为双线性协调位移场；uθ=[uθvθ]T，为由单元节点角位移分量θi引起的附加位移场。附加位移场为

式中：(ξ，η)为单元的自然坐标系。

将附加刚体转角位移而产生的单元边界位移沿单元边界设为三次分布，并对每一边引入广义协调条件。待定参数αi、βi(i=1，2，3，4)的详细推导过程参见文献［12］，代入式（3）可得GQ12 单元的总位移场，表示为

式中：N0i、Nuθi、Nvθi为单元对不同位移场的形函数。

式中：ξ、η和ξi、ηi分别为单元和单元节点的自然坐标系坐标。

GQ12的应变场为

单元刚度矩阵为

式中：B为单元应力-应变矩阵；D为弹性系数矩阵；|J|为雅可比矩阵行列式；t为单元厚度。

1.2 剪应变混合插值板元MITC4

基于一阶剪切变形理论的Mindlin 板元对位移场和转角场各自独立插值，由于单元边界只要求C0类连续，因此满足网格灵活性的需求，以及舵面等复杂外形结构的分析需要。一阶剪切变形理论放弃了Kirchhoff 理论的直法线假设，因此对于横向剪切变形明显的中厚板的分析，Mindlin 板元的预测效果相比Kirchhoff板元更好。但是，Mindlin板用于薄板时存在剪切闭锁和应力振荡等问题，不能满足几何显式加筋拓扑优化对有限元分析的要求。

缩减积分和选择积分方法列式简单，可解决剪切闭锁的问题，但根据约束类型等的不同，会带来零能模式问题。混合插值是一种比较理想的构造厚薄通用板元的方法，通过对单元面内应变和横向剪切应变使用不同的插值函数，避免剪切闭锁和零能模式问题。Bathe等［14-15］基于Mindlin板理论提出剪应变混合插值板元（mixed interpolated tensorial component，MITC4），计算结果较好，满足复杂结构的工程分析需要，如图1所示。

图1 板单元位移场Fig.1 Displacement field of plate element

由图1可得，板单元的横向剪切应变为

式中：θx、θy为x轴和y轴转角位移分量；ω为横向位移。

Mindlin板理论中，对于系统总位能公式中的弯曲应变能项，MITC4 单元使用与基于位移方法的Mindlin板单元相同的插值方法，广义位移通过相同的形函数独立插值为

式中：ωi、θxi、θyi分别为单元各节点处横向位移分量、x轴和y轴转角位移分量。

但是，对于横向剪切应变能项，如果采用相同的插值形式，会在薄板情况下出现剪切闭锁问题。Bathe 等［14-15］提出的MITC4 单元方案中，构造了一种在单元边和单元内满足剪应变一致的插值函数，插值形式为

式中：γAξz、γBηz、γCξz、γDηz分别为MITC4 单元在ξ-η-z坐标系下A、B、C、D四边中点的横向剪应变。

如图2 所示，对于x-y平面内任意凸四边形单元I-J-K-L，γξz、γηz的计算式为

图2 任意四边形单元Fig.2 Quadrilateral element

式中：detJ为雅可比矩阵行列式，

则有

同时，由于剪应变表达式定义在ξ-η-z坐标系下，需要转化到x-y-z坐标系下，转换形式为

式中：α为ξ轴与x轴夹角；β为η轴与y轴夹角。

1.3 验证算例

为验证GQ12 膜元与MITC4 板元耦合平板壳元的分析精度，设计一个四边形折板，其几何尺寸如图3所示。折板一侧约束，另一侧一点受集中力载荷F=-1 000 N 的作用，取结构E=210 GPa，v=0.3，分别对5 mm厚度及10 mm厚度折板算例求解结构应变。

图3 四边形折板算例Fig.3 Example of quadrilateral folded-plate

5 mm 厚度折板GQ12 膜元与MITC4 板元耦合平板壳元自编Matlab 程序的分析结果如图4（a）所示，采用商业有限元分析软件Ansys的分析结果如图4（b）所示。不同厚度折板加载节点和最大位移节点Z轴方向位移数值对照见表1和表2。

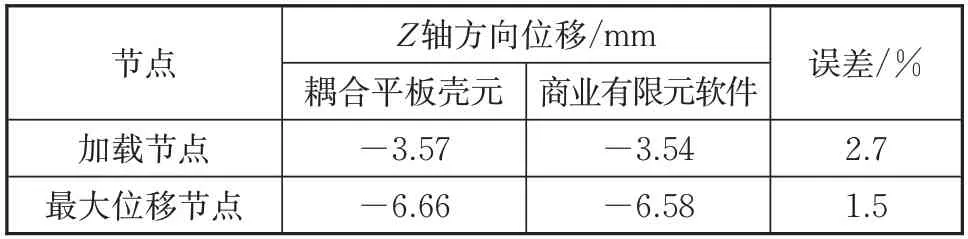
表1 5 mm厚四边形折板Z轴方向位移Tab.1 Z-axis displacement of the quadrilateral foldedplate with 5 mm thickness

表2 10 mm厚四边形折板Z轴方向位移Tab.2 Z-axis displacement of the quadrilateral foldedplate with 10 mm thickness

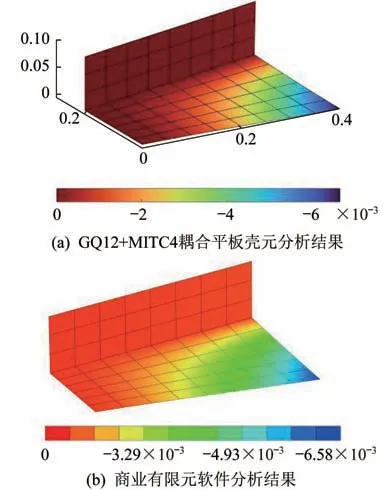
图4 四边形折板分析结果对比Fig.4 Analysis results comparison of the quadrilateral folded-plate

对以上算例结果进行对比，考察加载节点与最大位移节点Z轴方向位移值，相同约束和载荷条件下，5 mm 厚度折板与10 mm 厚度折板自编程序GQ12+MITC4 耦合平板壳元与商业有限元软件分析结果误差均＜4.5%，说明GQ12+MITC4耦合平板壳元具备厚薄通用性，计算精度良好。

2 自适应成长法

在自适应成长法结构加筋拓扑优化中，采用基结构法建立优化几何模型，其优点在于避免优化迭代过程中网格的重划分。参考承载和约束条件确定“种子点”的位置，如图5（a）所示。从“种子点”生长出来的加强筋根据一定规则成长或退化；生长到一定尺度可以“分歧”，再从“分歧点”继续生长，在下步迭代中参与成长与退化；退化到一定尺度则“消失”，如图5（b）—图5（c）所示。这个过程在优化迭代中反复进行，直至满足收敛条件。

图5 加强筋拓扑优化的自适应成长过程Fig.5 Adaptive growth process of stiffener topology optimization

2.1 数学模型及灵敏度分析

静载荷下，薄壁结构自适应成长法加筋拓扑优化问题的数学模型可以表述为：在给定的体积约束下，选择加强筋厚度作为设计变量，以结构在载荷条件下的总应变能为目标函数，逐步寻求最优解。其统一的数学模型可以表达为

式中：X为设计变量；xi为第i个活动筋板单元的厚度；n为加强筋单元的总数；Φ(X)为目标函数，即总应变能；V、V0分别为整体结构总体积和结构初始体积；η为体积约束因子；xmin、xmax为设计变量xi的取值下限和上限；g(X)为约束函数。

薄壁结构的柔度关于加强筋厚度的灵敏度计算公式为

式中：ui为第i加强筋单元的位移矢量；ki为第i加强筋单元的刚度矩阵。

2.2 优化设计流程

基于优化数学模型和自适应成长法基本原理，以移动渐近线法（method of moving asymptotes，MMA）作为迭代更新准则对结构分布进行寻优，具体流程如图6所示。

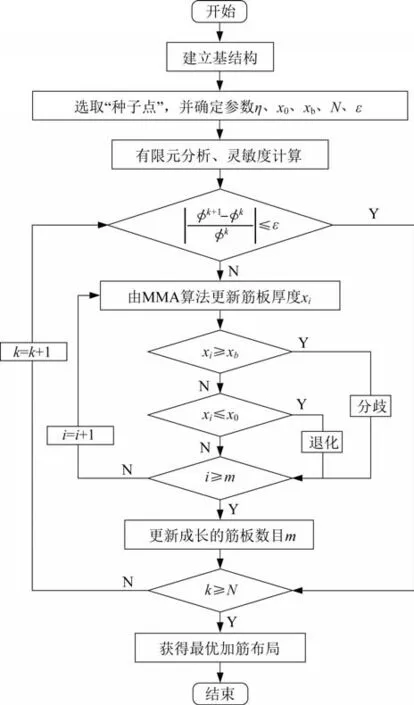
图6 自适应成长法优化设计流程Fig.6 Flow chart of optimization design of adaptive growth method

1） 建立基结构，设置设计域。

2） 选取“种子点”，设置优化参数。参考结构的载荷和支撑情况，选取基结构上若干节点作为“种子点”，给定加强筋的初始厚度x0、分歧临界值xb、体积约束因子η、收敛容差ε以及最大迭代次数N。

3） 灵敏度分析。对结构进行有限元分析，通过解析法计算活动筋板单元的灵敏度。

4） 成长和退化。判断收敛状态，如果满足筋板成长条件，通过MMA 算法更新xi；如果筋板厚度达到分歧临界值xb，该单元进行分歧；如果满足退化条件，该单元退化。

3 舵面结构加筋布局优化

3.1 舵面基结构构建

根据舵面几何形状，在优化设计前构建拓扑优化基结构，舵面外层为蒙皮结构，定义厚度为0.5 mm。选择舵面内部空间区域作为设计域，定义基结构初始厚度为0.5 mm，如图7 所示。由于舵面的几何特征，构成基结构的单元为任意凸四边形单元，GQ12 膜元和MITC4 板元耦合构造的四边形等参平板壳元适用于舵面基结构的有限元分析。

图7 舵面优化初始基结构Fig.7 Initial ground structure of rudder structure for optimization

3.2 基于自适应成长法的加筋布局

根据舵面的实际工作状态，对其约束施加于舵轴，受单侧横向均布载荷。因此，本文以舵面舵轴处约束点为自适应成长法的“种子点”，以整体结构应变能最小为设计目标，骨架结构体积为约束条件，对舵面进行加筋拓扑优化，寻找最优的骨架结构分布。优化的数学模型为

式中：T为设计变量，为每个活动筋板的厚度；U(T)为目标函数，即整体结构应变能；V、V0分别为加筋舵面结构总体积和初始实体舵面结构体积；η=20%为体积约束因子。

经过拓扑优化设计得到的舵面内部最优加筋布局如图8 所示。图中呈现出清晰的分枝结构，拓扑形态合理且具有较优的可制造性。

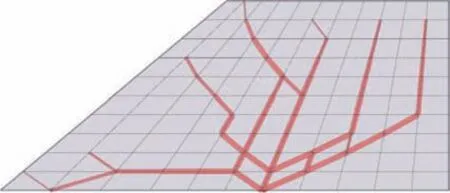
图8 拓扑优化后的舵面加筋布局Fig.8 Rudder stiffener layout obtained by topology optimization

优化过程迭代曲线如图9 所示。优化迭代过程中，应变能与初始应变能比值在前10个迭代步中下降较快，随后迭代过程逐渐平缓直至收敛，优化效果理想，验证了GQ12膜元和MITC4板元耦合四边形等参平板壳元分析的准确性，自适应成长法的有效性及优化结构的合理性。

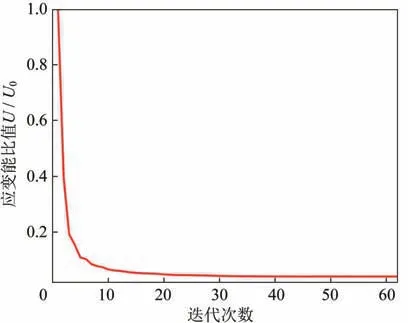
图9 舵面结构加筋布局优化迭代曲线Fig.9 Iteration history curve of rudder stiffener layout

3.3 设计结果分析

为了评估加筋拓扑优化效果，利用耦合四边形平板壳元建立舵面的传统蒙皮-网格式骨架设计模型，如图10所示。对文献［1］中介绍的传统骨架设计进行建模并分析，计算得到拓扑优化前后舵面的整体结构应变能，如图11所示。

图10 舵面传统骨架设计Fig.10 Traditional rudder skeleton design

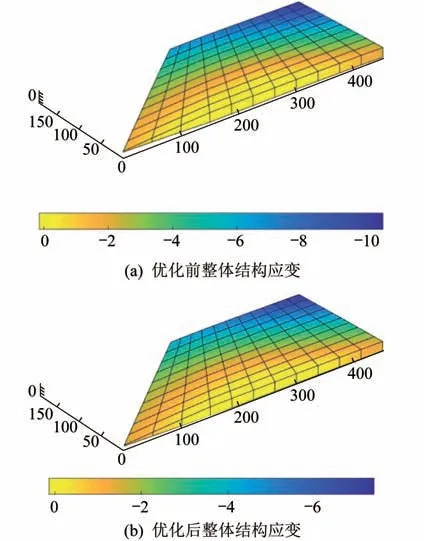
图11 舵面结构优化前后整体结构应变Fig.11 Strain of overall structure before and after rudder structure optimization

对比传统网格式骨架设计与加筋拓扑优化后舵面整体结构的应变能数值以及结构质量，结果见表3。由表3可见，优化后结构的应变能为17.28 J，较传统设计25.80 J降低了33%，结构刚度得到增强；传统骨架设计的质量为1.19 kg，优化后结构的质量降低了29%。

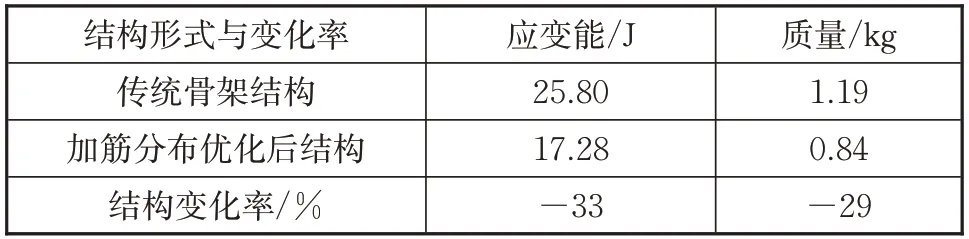
表3 舵面结构优化前后性能比较Tab.3 Performance comparison before and after rudder structure optimization

4 结束语

本文利用GQ12 膜元与MITC4 板元耦合构造了四边形等参平板壳元，通过有限元分析实现了基于自适应成长法的不规则薄壁结构的加筋设计。随后以轻质、高承载的舵面结构为例，获得了静载荷状态下舵面内部的最优骨架布局。经过对优化前后舵面结构的性能对比，验证了GQ12膜元与MITC4板元耦合平板壳元分析工具的准确性和实用性，同时验证了自适应成长法对舵面优化设计的有效性。