基于虚拟激励法的多激励振动试验数值分析

王肇喜，翟师慧，赵 凡，王者蓝，谢夏阳

（上海航天精密机械研究所，上海 201600）

0 引 言

振动环境试验是目前航天产品可靠性和环境适应性最主要的检验手段，用于发现产品设计上的缺陷、工艺上的不成熟及可靠性的薄弱环节，为产品设计及工艺上的改进与优化指明方向［1］。

细长型飞行器的振动环境试验为工程中的一大难题，由于此类飞行器外形细长，振动试验中其超出振动台面的悬臂部位过多，振动响应悬臂端低频放大、高频衰减，使试验室状态下飞行器的振动环境较之飞行状态有较大失真，飞行器各部位的过试验、欠试验现象异常严重。

多输入多输出（multi-input multi-output，MIMO）振动试验技术采用两（多）个振动台提供激振力，使试件不同部位产生不同的振动响应。这种试验方式能够更加准确地模拟细长型飞行器各种飞行状态下的振动环境，有效地避免传统单振动台试验方法中振动应力集中的现象，为力学环境试验技术的重大进步和未来发展趋势［1］。

目前，国内少数航空、航天单位已经开始应用MIMO振动试验方法。但由于我国现有的试验标准对该类型试验的描述较为笼统，并且国内对互谱的作用、双振动台模拟互谱的可实现性及其效果的研究不够透彻［1-2］，加之此项技术的军事背景，使得国外相关的技术资料难以获得，因此，我国工程人员在进行MIMO振动试验时，面对控制参数的选取和试验条件的制定等问题，大多凭借工程经验，采用试验中不断变换、试探、摸索的方法，这将会走很多弯路，造成大量人力、物力、财力的浪费，而最终的试验效果也难以达到最优。

本文基于虚拟激励法、逆虚拟激励法原理［3-5］，研究MIMO 随机振动试验中控制谱矩阵设置的可实现性，并对某一细长型飞行器模拟件在不同控制点数量、控制参数设置情况下的振动试验进行数值模拟，分析控制点数量及控制互功率谱对双台振动试验的影响。

应用此方法，在正式试验前对各种试验方案进行预试验，使试验人员提前了解振动试验中不同控制点位置、参数设置所产生的效果，提前知晓试件在试验过程中各部位振动响应情况，提前评判所选用的试验仪器设备能否顺利完成试验，避免在试验条件定制过程中的盲目性，由此可降低大型复杂试件振动试验的风险，获取最优的试验设计方案。

1 随机振动问题的分析方法

1.1 随机振动基本理论

对于多输入多输出振动系统，其输入、输出谱密度矩阵为［5-6］

式中：ω为圆频率；n为系统的输入或输出个数。

对角线元素为各点的自功率谱，它表述随机振动在频域的能量分布，非对角线元素为两点间的互功率谱，它含有相干系数和相位这两个参数的信息，表达式为

式中：γxixj为相干系数；φxixj为相位差；i，j为公式索引变量。

激励与响应的功率谱密度矩阵的关系式为［6-7］

1.2 虚拟激励法理论

直接使用式（3）计算MIMO 随机振动问题，计算量太大，因此林家浩等［8］提出虚拟激励法，这种方法在不降低计算精度的前提下，大大降低了求解该类问题的计算量。

虚拟激励法［3-4］基本手段为矩阵的对角化变换，MIMO 系统的输入、输出功率谱密度矩阵Sxx(ω)为Hermite 矩阵，根据矩阵理论，Hermite 矩阵一定酉相似于对角形矩阵，且其特征值为实数。

则功率谱密度矩阵可转化为

式中：λ1(ω)～λk(ω)为矩阵Sxx(ω)的特征值；k为矩阵Sxx(ω)的秩；U1(ω)～Un(ω)为酉矩阵的列向量；Ui*(ω)为Ui(ω)的共轭转置。

式（4）可转化为

1） 各激振力相互之间完全相干时，Sxx(ω)的秩k=1，式（6）可改写为

2） 各激振力相互之间完全不相干时，Sxx(ω)为对角线矩阵，式（6）可改写为

3） 激振力部分相干时，Sxx(ω)的秩为k（k≤n），式（6）可改写为

由于xi(ω)为列向量，且相互正交，则可将MIMO随机振动系统的输入项视为几个相互正交的虚拟简谐激励力xi(ω)eiωt叠加的效果。

将式（6）代入式（3）得：

则

其中

同理，根据式（11），可将MIMO 系统的振动响应视为虚拟简谐激励xi(ω)eiωt产生的虚拟简谐响应yi(ω)eiωt叠加的效果，其虚拟激励与虚拟响应的关系见式（12）。应用虚拟激励法，求解MIMO 系统随机振动响应的基本流程为：① 将输入的谱密度矩阵分解为式（6）的形式，构造虚拟激励xi(ω)；② 由式（12）得出虚拟响应yi(ω)；③ 由式（11）输出功率谱密度矩阵。

1.3 逆虚拟激励法理论

逆虚拟激励法［5］多用于随机振动载荷识别问题领域，即已知结构的随机振动响应和结构的固有特性（频响函数矩阵），反推结构所受的激振力。逆虚拟激励法的计算流程为：① 将Syy(ω)改写为式（11）的形式，构造虚拟响应yi(ω)；② 由式（12）构造方程，求解xi(ω)；③ 由式（6）得出激振力的功率谱密度矩阵。

2 双振动台试验模型分析

两个振动台组成的双台振动试验系统如图1 所示，其中加速度传感器、电荷放大器、计算机、功率放大器、振动台构成一个闭环反馈控制系统。试验过程中闭环控制系统不断反馈修正，调整两振动台输出的激振力，使试件上控制测点的振动响应功率谱与预设值相等。

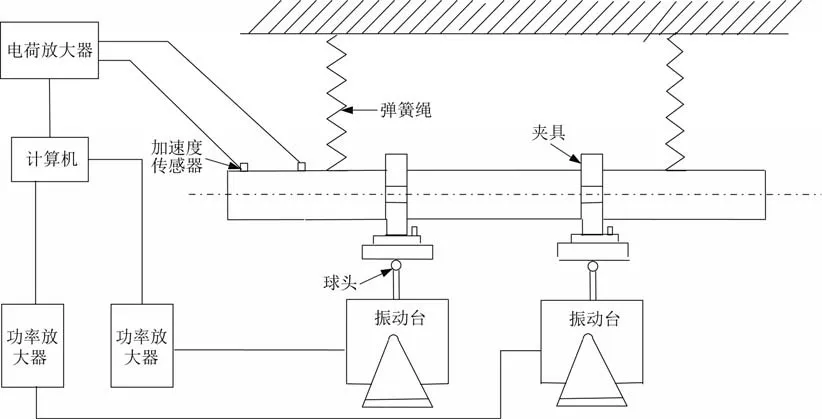
图1 双台振动试验系统Fig.1 The system of double vibration test

不同厂家的振动控制系统，其控制器的控制迭代算法各有不同，但经反馈修正，最终稳定时，两个振动台输出的激振力都使控制点实际振动响应与预设值相等或者偏差最小。根据此原理，假设控制器性能理想，对细长型飞行器双振动台试验建立力学模型，并进行分析。

2.1 双振动台试验分析模型的建立

由于球头（见图1）的作用，将试件与振动台连接处的转动自由度释放，且弹簧绳的拉力与试件的重力相抵消，则试件的边界条件可视为自由状态，其受力模型如图2所示，图中fi、fj分别为i、j位置点所受的力。

图2 细长型飞行器的受力模型Fig.2 The mechanical model of slender aircraft

该受力模型的动力学方程为［9-10］

式中：M、C、K、F分别为飞行器的质量矩阵、阻尼矩阵、刚度矩阵、所受的力矩阵。

式（13）经傅里叶变换表示为

即

其中，F(ω)为

式中：fi(ω)、fj(ω)分别为图2 中i、j位置点所受的力谱。

结构的整个传递函数矩阵，可由模态测试的结果，根据模态叠加法［11-12］近似得到：

式中：ωi为第i阶固有频率；ξi为第i阶模态阻尼比；Φi为关于质量阵归一化的第i阶模态阵型。

2.2 双振动台试验控制谱矩阵可实现性分析

对于双振动台试验系统，可视为一个两输入多输出的系统，输入的谱密度矩阵为2×2的矩阵。

若控制点的个数为m时，则控制谱密度矩阵Syy(ω)的维数为m×m，将Syy(ω)分解为式（11）的形式，yi(ω)为m维列向量。双台振动试验系统下，逆虚拟激励法中式（12）为

1） 当控制点的个数=2 时，H(ω)m×2为方阵，在H(ω)非奇异的情况下有唯一解（若矩阵H(ω)奇异，则有无穷多解），由式（20）可直接求出xi(ω)，解得使控制测点的实际振动响应与预设的谱值完全一致的两激振力。

2） 当控制点的个数＞2 时，H(ω)m×2为长方振，此时式（20）理论上无解，只能求其最小二乘解，即试验控制系统经反复修正迭代后，产生的最优激振力，只能保证控制测点的实际振动响应值与预设的值差异最小，不能实现真实响应值与预设值完全一致。

因此，采用多点（控制点数＞2）控制方式，一般情况下无法使各控制测点的实际振动响应值与预设值完全一致；双振动台试验系统采用两点控制方法，输入完整的控制谱矩阵，无论控制测点互功率谱的相干系数与相角为多少，理论上都可以使测点的实际振动响应与预设的功率谱密度矩阵完全一致。

3 不同试验条件下双台振动试验的数值模拟

工程中，双振动台试验主要分为两点和多点（大于两点）两大类控制方式，控制测点的相干性又分为完全相干、完全不相干及部分相干等情况。针对工程中常用的控制方式，选取具有代表性的情况进行数值模拟。

研究对象为某细长型飞行器模拟件，其长3 100 mm、外径200 mm、壁厚65 mm，为铝质结构。该试件的模态参数由有限元分析软件MSC.Nastran计算得到，计算时将试件划分为20 个梁单元、21 个节点，约束其纵向自由度。飞行器模拟件有限元离散后模型如图3 所示，飞行器模拟件前十阶固有频率见表1，其中前两阶为刚体模态。

表1 试件固有频率Tab.1 The inherent frequency of analog sample

图3 试件的有限元模型Fig.3 The finite element model of the test specimen

应用Matlab 软件编程计算，模拟各种控制方式下的试验结果，计算流程如下：

1） 取模态阻尼比为0.03，由前十阶模态参数，根据式（17）—式（19）得整个结构的频响函数矩阵；

2） 由控制点的控制谱密度矩阵，采用1.3 节逆虚拟激励法计算流程，计算控制点位置振动响应达到控制谱值时，两激振力的自、互功率谱密度；

3） 由计算得到的激振力的自、互功率谱密度，采用1.2 节虚拟激励法计算流程，计算得到试件各点的振动响应。

3.1 两点控制方式的模拟

取试件上点1、21 为控制点（见图3），两个控制点的自功率谱密度如图4所示。控制测点的互功率谱分别采用3种控制方式［13-15］：① 控制点全相干，两控制点的相干系数为1，相角为零；② 控制点完全不相干，两控制点的相干系数为零；③ 控制点部分相干，两控制点的相干系数为0.5，相位差45°。

图4 控制点的振动谱Fig.4 The vibration spectral of the control points

3 种控制方式的自功率谱相同，互功率谱各异。3 种控制方式下，试件上各点振动响应的自功率谱密度、加速度均方根值分别如图5 和图6 所示。控制测点的互功率谱值，对试件振动响应的影响显著。

图5 各种控制条件下试件上各点振动响应的自功率谱Fig.5 The auto-power spectral density of various response points under different control conditions

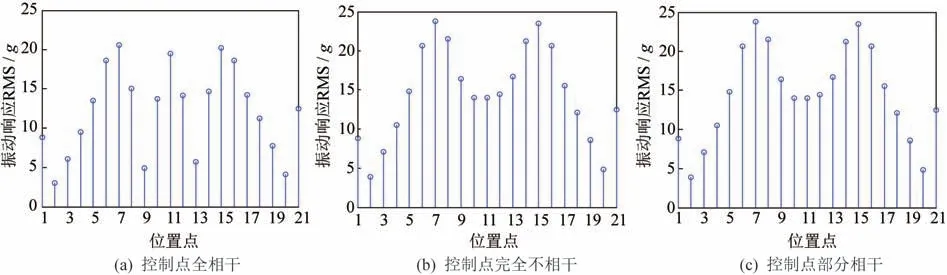
图6 各种控制条件下试件上各点振动响应的加速度均方根值（RMS）Fig.6 The acceleration RMS of various response points under different control conditions

各种控制方式下，控制点位置振动响应达到控制谱时，试件所受激振力的自功率谱密度、相干系数、相位差如图7—图9 所示。其中，控制点完全相干时，两激振力也完全相干，如图8（a）所示；当控制点不完全相干时，两激振力在频域内的相干系数起伏变化，如图8（b）、图8（c）所示。

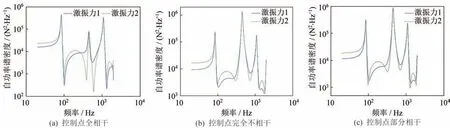
图7 各种控制条件下试件所受激振力的自功率谱Fig.7 The auto-power spectral density of the exciting force under different control conditions

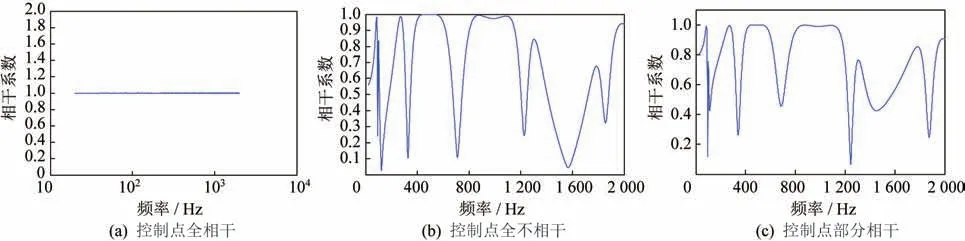
图8 各种控制条件下试件所受两激振力的相干系数Fig.8 The coherence coefficient of the exciting force under different control conditions

图9 各种控制条件下试件所受两激振力的相位差Fig.9 The phase difference of the exciting force under different control conditions

3.2 多点（三点）控制方式的模拟

多点控制方式：取试件上点1、10、21为控制点（见图3），各点的自功率谱密度如图10所示。点1、点21的相干系数为0.2，相位差为0，点10 与1、21 的相干系数为0.5，相位差为90°。该种控制方式下，控制测点处的实际振动响应无法与预设值完全一致，如图11所示。

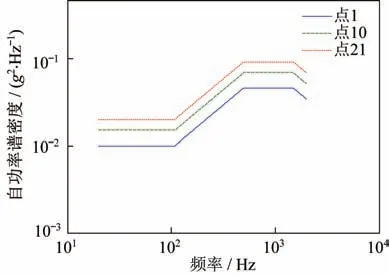
图10 控制点控制谱Fig.10 Reference Auto-power spectral density

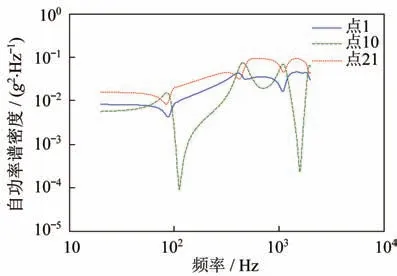
图11 试件上各点的振动响应Fig.11 Auto-power spectral density of the simulated sample

试件各点振动响应的均方根值如图12 所示。由图可见，这种控制方式各控制测点无法与控制谱完全一致，但可使试件各点振动响应分布比较均匀。

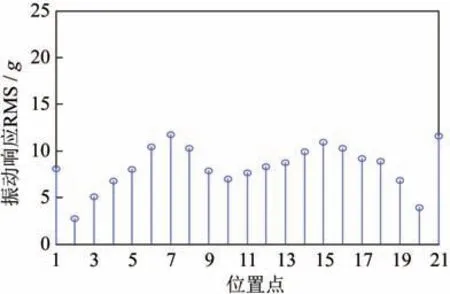
图12 试件各点振动响应的加速度均方根值（RMS）Fig.12 Acceleration RMS of the simulated sample

试件所受的激振力的自谱、相干系数、相角如图13—图15所示。

图13 试件所受激振力的自功率谱Fig.13 Auto-power spectral density of the exciting force

图14 试件所受激振力的相干系数Fig.14 Coherence coefficient of the exciting force

图15 试件所受激振力的相位差Fig.15 Phase-difference of the exciting force

3.3 分析总结

由3.1 节与3.2 节的算例可知，两点控制方法可以使控制点位置的振动响应与预设值完全一致（图5中，点1、点21的实际振动响应），多点（控制点数＞2）控制方式无法使控制测点的实际振动响应值与预设值完全一致（图11）。

在振动试验前，可对各种控制方式进行预试验模拟分析，根据试件各点的振动响应自功率谱及加速度均方根值，选择合适的控制方式。除此之外，还需考虑激振力的因素，如图7（a）所示，这种控制方式下所需的激振力自功率谱密度跳变较大，有可能超出试验硬件设备的允许范围，使控制效果变差。因此，应尽可能选择所需的激振力自功率谱变化相对缓和的控制方式，如图7（b）、图7（c）所示。

受激振点位置距离的影响，实际试验时激振力之间相互干扰，两激振力在低频段的相干系数较大，受这一因素的制约，应尽量避免选择所需的激振力低频段相干系数过小的控制方式，如图8（b）所示，该种控制方式所需激振力在20～50 Hz 之间的相干系数约为0.55，实际试验有可能无法实现，使控制效果变差。

4 结束语

通过针对细长型飞行器开展基于虚拟激励法的多点激励振动仿真分析，可得到如下结论：

1） 虚拟激励法、逆虚拟激励法的应用可有效确保细长型飞行器MIMO 随机振动试验的数值模拟计算精度，大大降低了问题的计算量，使试验前对各种试验条件的预试验分析成为可能。

2） 双台振动试验系统在采用两点控制方法时，输入完整的控制谱矩阵后，理论上控制点的实际振动响应与预设的功率谱密度矩阵完全一致。

3） 采用多点（控制点数大于激励点数）控制方法时，一般情况下各控制测点的实际振动响应值无法与预设值一致，输出的激振力只能保证控制测点实际的振动响应与预设值的偏差尽可能小。