基于多应力仿真分析的舵机加速试验剖面设计方法

王海东，刘 博，王肇喜，蒋 刚

（上海航天精密机械研究所，上海 201600）

0 引 言

随着空天威胁目标作战能力的提升，高超声速、长航时、大过载、强机动等特性已经成为我国新一代装备的研制要求［1］。为确保武器装备的可靠性，机电产品的地面试验验证是研制过程中必不可少的环节［2］。目前，机电产品的失效问题大多发生在温度、湿度和电应力等多种因素组合下［3-4］。环境应力单独施加和综合施加在机电产品上会产生不同失效加速效果，多应力环境加速试验更易激发和暴露机电装备内结构故障［5-6］。为了使武器装备更加适应严酷复杂的服役环境，可基于多应力加速试验数据，分析展开机电装备可靠性分析和寿命预测［7］。电子科技大学魏郁昆［8］针对某型号惯性导航系统设备元器件的失效模式、失效机理进行研究，确定该型号惯性导航的薄弱环节，设计加速退化实验，并得到环境应力水平的范围和保守的寿命估计值。北京航空航天大学苗学问［9］针对工程中缺少有效方法处理加速试验中出现的无失效数据的情况，提出一种恒定应力水平下的无失效加速试验可靠性分析方法，通过将加速应力水平下的无失效寿命试验数据转换到正常的应力水平，实现产品无失效加速试验的可靠性评估和寿命预测。西北工业大学赵志草等［10］提出了加速退化试验与加速试验相结合的评估方法，实现加速退化试验数据到加速试验数据的转化，提出的可靠性评估算法可以避开大量针对加速退化模型分析和建模的研究工作，能较好地对高可靠、长寿命产品进行可靠性评估。南京理工大学肖坤［11］以某弹用O形橡胶密封圈为研究对象，采用加速退化试验方法对其进行试验，研究了其性能参数退化规律并准确预测了其贮存寿命。北京强度环境研究所赵帅帅等［12］针对温度循环应力下加速试验数据处理困难而限制其应用的问题，提出了一种基于修正Coffin-Manson模型的加速试验设计与评估方法。以电子组件为对象，建立了温度循环试验的加速因子模型，用一元和二元线性回归评估了加速因子模型的参数，进而对产品寿命进行外推，得到了正常应力条件下的可靠度函数，有效地评估产品在温度循环应力下的寿命。

目前开展的各项加速试验往往只考虑单应力加载，其应力强度与作用时间，基本上选取统一的量级与时间，很少有针对不同服役环境下的不同产品特性，分别制定有效的组合载荷工作剖面。机电产品的性能差异显著，经历的环境也各不相同。采用相对统一的标准不利于暴露产品在实际工况中出现的故障，在前期实验室验证阶段，对可能出现的故障及其失效物理认识不足，采集的基础数据不够充分，难以准确计算产品的可靠度。

以某型号导弹舵机为例，针对周期性载荷加速试验开展研究。此类加速试验剖面的设计主要包括加速载荷量级以及周期的确定。为减少试验时间与试验样件数量，首先采用Workbench 软件进行模型的仿真建模，对仿真模型按照步进的方式加载应力，通过仿真分析确定舵机在各应力类型下的工作极限；其次根据舵机的工作极限和实际工况建立初始加速试验剖面，计算得到舵机的疲劳寿命；最后根据得到的疲劳寿命建立舵机的多应力综合加速因子模型，结合加速比≥5的要求来修正，确定最终的舵机加速试验剖面。

1 基于仿真分析的初始试验剖面设计

1.1 舵机的有限元模型

在长期的试验中，某型导弹舵机系统主要会受到温度、湿度和电应力等3种应力的影响，产生丝杆卡死和电路板管脚断裂等失效模式，据此，本文的舵机加速试验剖面由温度、湿度和电应力等环境应力综合作用的循环周期构成。其中，温度循环的参数包括温度极限、温度变化率和循环数；湿度参数包括应力量级和驻留时间；电应力参数包括应力量级和驻留时间。根据标准GJB 1032、GJB 150 和GJB 4239，加速试验载荷量级的选取一般尽量接近工作极限水平，因此，设计加载的初始剖面首先要得到温度、湿度和电的工作极限。本文首先采用有限元模型（finite element model，FEM）得到结构中应力或应变的最大响应点，确定危险位置。再进行步进式加载仿真分析，得到步进载荷下危险区域的结构应力或应变响应。最后通过极限阈值确定对应的工作极限。

舵机主要包括传动机构和传感电路，其中传动机构包括滚珠丝杠，传感电路包括电位计。伺服电机接收舵偏指令，与舵翼实际偏转角测量信号比较后，输出控制信号带动传动机构动作。传动机构将伺服电机高转速、低扭矩特性传递到舵翼，形成低转速、高扭矩的转动特性。伺服电机带动丝杠绕轴旋转，丝杠上装有套筒，套筒与摇臂连接，将直线位移转化为角位移，带动导弹舱外舵翼旋转。

为保证计算结果的准确性和运算成本的合理性，将滚珠丝杠系统零件与传感电路板的建模进行合理简化。将轴、丝杠螺母分别简化为等直径的光杆和通孔。轴与轴承、轴承与轴承座孔、丝杠螺母与滚珠丝杠之间的接触热传导利用有限元中的接触热单元来实现。舵机传感电路主要封装形式为四方扁平封装。电路板上除四方扁平封装和小外形封装等不具有封装焊点的元器件，采取等效质量块的方法，以原尺寸按照绑定的方式固定在印制电路板（printed circuit board，PCB）板上。忽略焊点焊接过程中产生的空洞、裂缝及加工缺陷；不考虑基板中通孔和布线等细微结构；假设芯片为封装系统唯一且均匀的热源且忽略辐射换热。滚珠丝杠系统与电路板有限元模型如图1所示。

图1 舵机主要组件的有限元模型Fig.1 FEM of the main components of the steering gear

除焊点外，各结构材料属性与温度无关的线性各项同性，见表1。滚珠丝杠的材料为铬钢，电机支座和轴承支座为灰铁。焊点材料为Sn37Pb63，焊点视为弹性模量随温度变化的非线性材料，采用Anand 黏塑性统一本构方程来描述焊点热力学特性。

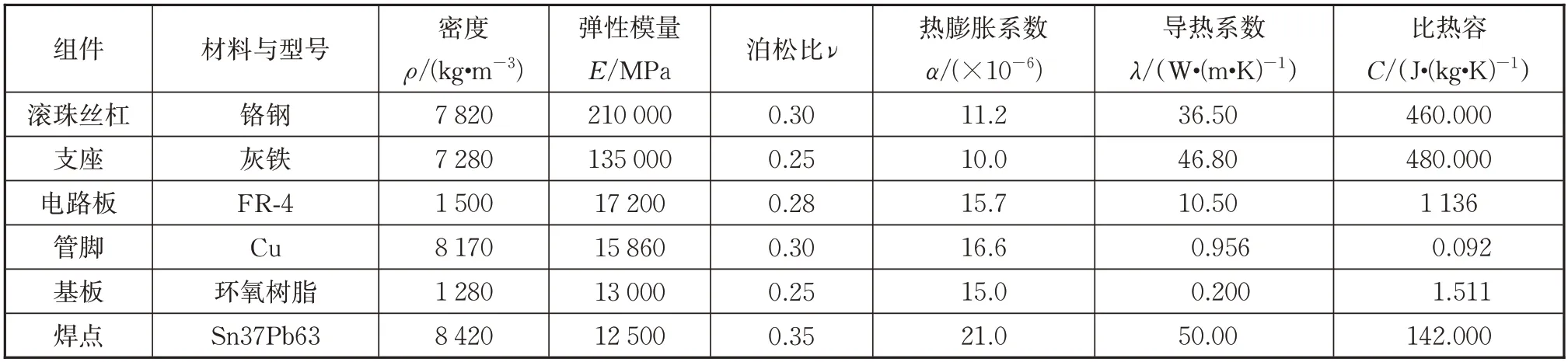
表1 舵机主要组件的材料属性Tab.1 Material properties of the main components of the steering gear

1.2 基于仿真确定载荷初始剖面

通过温度、湿度和电流步进加载的仿真分析，得到滚珠丝杠与电路板的极限工作应力，具体加载参数见表2。其中驻留时间设为较大的值30 min，保证仿真分析得到的是稳态响应结果。

表2 步进加载参数Tab.2 Step load parameters

滚珠丝杆在低温载荷-70 ℃和高温载荷120 ℃下的变形云图分别如图2 和图3 所示。云图中最大变形点均位于丝杠和螺母接触处，因此该接触处为滚珠丝杆的薄弱环节。经低温与高温的步进加载仿真分析，当温度＜-60 ℃或＞110 ℃时，丝杠和螺母接触处的变形会大于最小的卡死阈值31.5 μm，因此滚珠丝杆的低、高温工作极限分别为-60 ℃和110 ℃。

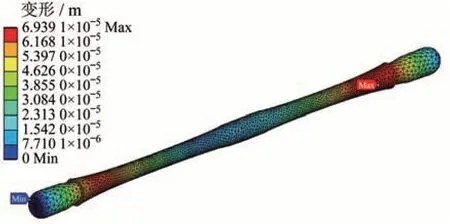
图2 滚珠丝杆在低温载荷-70 ℃下的变形云图Fig.2 Deformation nephogram of ball screw under-70 ℃ low-temperature load

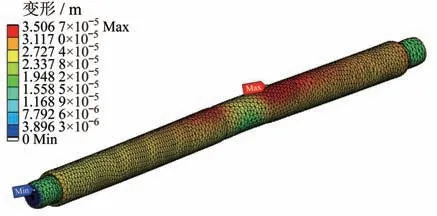
图3 滚珠丝杆在高温载荷120 ℃下的变形云图Fig.3 Deformation nephogram of ball screw under 120 ℃ high-temperature load

传感电路在低温载荷-70 ℃和高温载荷120 ℃下的应力分布云图分别如图4 和图5 所示。云图中最大应力点均位于塑封器件管脚处，因此该处为传感电路的薄弱环节。经低温与高温的步进加载仿真分析，当温度＜-50 ℃或＞90 ℃时，塑封器件管脚处的应力会大于最小的管脚断裂应力阈值49.3 MPa，因此，传感电路的低、高温工作极限分别为-50 ℃和90 ℃。滚珠丝杆和传感电路都是舵机的重要组成部分，综合两者工作温度区间的交集，得到最终舵机的低、高温工作极限为-50 ℃和90 ℃。

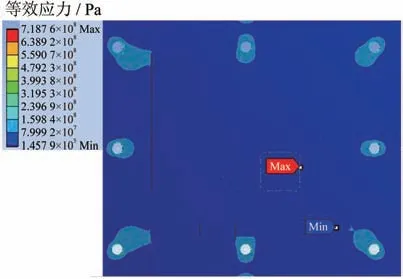
图4 传感电路在低温载荷-70 ℃下的应力云图Fig.4 Stress nephogram of the circuit board under-70 ℃ low-temperature load

图5 传感电路在高温载荷120 ℃下的应力云图Fig.5 Stress nephogram of the circuit board under 120 ℃ high-temperature load

试验与仿真分析表明，湿度与电流对滚珠丝杆的影响均较小，因此，湿度与电流工作极限分析的重点在于传感电路板。湿应力通过湿膨胀系数与潮湿饱和度之间的函数关系进行计算。为了得到舵机在湿气分布下产生的湿应力情况，可以通过有限元建立湿气扩散模型，然后通过热-湿参数转换，将湿扩散过程通过有限元中的热传导分析模块来代替［13-14］。热-湿参数转换对应关系见表3，其中温度T与相对湿度H对应、密度ρ与单位常量对应、传导率λ同D·Csat（湿扩散率与饱和湿度的乘积）对应、比热C与饱和湿度Csat对应。

表3 热-湿参数转换对应关系Tab.3 The corresponding relation between heat and humidity parameter

传感电路在相对湿度100%下的应力分布云图如图6 所示，图中最大应力点位于塑封器件管脚处，因此，该处为传感电路的薄弱环节。经相对湿度步进加载仿真分析，当相对湿度＞80%时，塑封器件管脚处的应力会大于最小的管脚断裂应力阈值49.3 MPa，因此，传感电路的相对湿度工作极限为80%。

图6 传感电路在相对湿度100%下的应力云图Fig.6 Stress nephogram of the circuit board under 100% relative humidity

传感电路在实际工作过程中伴随着消耗电功率，并转变成生热量，会引起舵机系统传感电路的电子器件发生局部过热，导致电子器件热变形和应力集中问题加剧，最终影响舵机工作性能。因此，舵机的电载荷分析最终要转化为热效应分析，重点针对电流来开展仿真分析［15-16］。传感电路在电流载荷5 A 下的应力分布云图如图7 所示，图中最大应力点位于塑封器件管脚处，因此该处塑为传感电路的薄弱环节。经电流步进加载仿真分析，当电流＞4 A 时，塑封器件管脚处的应力会大于最小的管脚断裂应力阈值49.3 MPa，因此传感电路的电流工作极限为4 A。

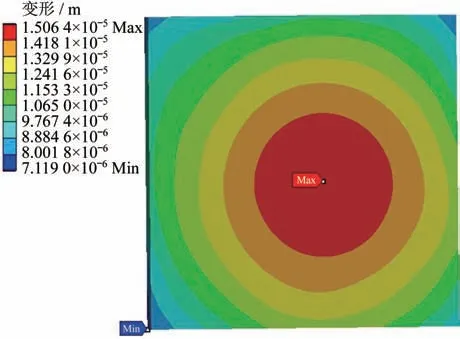
图7 传感电路在电流载荷5A下的应力云图Fig.7 Stress nephogram of the circuit board under 5A current load

针对本文的舵机系统，取安全系数0.8 来确定各载荷的应力极限值，并参考标准GJB 1032、GJB 150和GJB 4239，确定初始加速试验剖面的相关参数为：低温-50 ℃，高温90 ℃，相对湿度80%，电流4 A，温变率10 ℃/min，温度驻留时间120 min。考虑到较大的湿度载荷在低温环境下会产生凝露，此时对舵机样件通电将导致系统短路，因此决定在高温驻留期间对舵机样件施加湿度载荷，待温度载荷和湿度载荷都达到稳定后施加瞬间大电流（持续时间10 s）；在低温驻留期间不考虑湿度载荷，但同样施加瞬间大电流（持续时间10 s）。根据上述确定的试验周期和试验载荷，建立初始加速试验剖面如图8（a）所示。

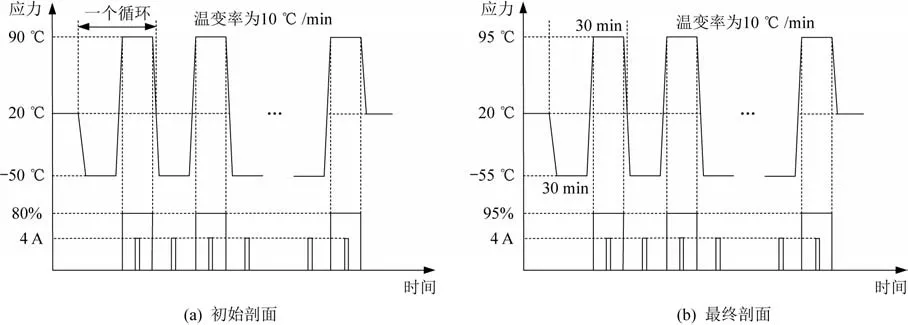
图8 加速试验剖面Fig.8 Accelerated test load profile

2 基于加速比修正试验剖面

2.1 多应力加速因子模型

加速因子（或加速比）是某种条件下的加速试验与基准应力条件的试验达到相等累计失效概率所需时间之比。计算加速因子需要建立产品性能参数的与给定应力间的关系，通常称为加速模型。分析导弹舵机在温-湿-电综合作用下的失效情况，需要依据加速试验应力类型的不同，采用不同的加速模型。通常单温度应力可以使用艾林模型，单湿度应力或单电应力可以使用逆幂律模型［17］。广义艾林模型由逆幂律模型和艾林模型两部分组成，可以描述产品寿命与温-湿-电综合应力之间的关系。因此，导弹舵机综合应力下的加速模型可以采用广义艾林模型，根据温-湿-电综合加速模型可以确定温度-湿度-电应力综合加速因子（AF），其表达式为

式中：Is、Hs、fs、Tsmax、Tsmin为加速应力条件；I0、H0、f0、T0max、T0min为正常工作应力条件；η0为试验对象的产品特征寿命；I为电流；H为相对湿度；f为循环频率；Tmax为最高温度；Tmin为最低温度；Ea为激活能；k为玻尔兹曼常数（值为8.617×10-5eV/K）；a、b、c、d、e为待定系数。

2.2 基于多应力仿真分析

等效塑性应变由于塑性累积效应逐渐增大，当等效塑性应变累积到一定程度时，材料发生疲劳破坏。根据1.2 节，在温度-湿度-电的多应力作用下，传感电路的塑封器件管脚为薄弱区域。由于电路板Sn63Pb37这类焊点失效模型通常为低周疲劳失效，因此采纳基于塑性应变预测模型中的Coffin-Manson 方程［18］。考虑到热循环温度和频率的影响，Coffin-Manson方程被修正为

式中：Nf为材料的疲劳寿命；Δγp为等效塑性剪切应变范围；εpmax为等效塑性应变最大值；εpmin为等效塑性应变最小值；εf为疲劳韧性系数；β为疲劳韧性指数；tm为平均温度；nf为材料的循环周期数。

根据一个循环相关的剖面参数（最高温、最低温、相对湿度、电流、驻留时间），可以通过仿真得到对应的疲劳寿命，再将疲劳寿命除以一个周期时长即可得到破坏循环数。舵机多应力仿真疲劳寿命见表4。

表4 舵机多应力仿真疲劳寿命Tab.4 The fatigue life of steering engine under multistress condition

利用舵机在不同应力量级下仿真得到的疲劳寿命，使用最小二乘法对温度-湿度-电的多应力综合加速模型进行曲线拟合，得到加速因子模型参数的待定参数值为：a=1.986 1，b=9.695 2，c=2.944 7，d=0.225 0，e=6.543 3。

2.3 加速试验剖面修正

根据舵机实际工况要求，选取舵机正常工作条件为：I0=1 A，H0=10%，T0max=30 ℃，T0min=10 ℃，f0=1/86 400（周期T0=24 h），通过多应力加速模型计算，得到正常工作条件下的疲劳寿命为3 186 min。初始加速试验剖面的加速条件为：Is=4 A，Hs=80%，Tsmax=90 ℃，Tsmin=-50 ℃，fs=1/14 400（周期Ts=4 h），通过多应力加速模型计算得到初始加速试验剖面条件下的疲劳寿命为747 min，初始加速试验剖面下的加速比为3 186/747=4.26。再通过迭代得到满足加速比≥5 的剖面参数为：低温-55 ℃，高温95 ℃，湿度95%，电流4 A，高低温驻留时间30 min，温变率为10 ℃/min。多应力加速试验剖面如图8（b）所示。其中，湿度应力在高温驻留阶段施加，待温度和湿度都稳定后，施加瞬间大电流（持续10 s），且在低温驻留期间不考虑湿度载荷，但同样施加瞬间大电流（持续时间10 s）。

3 结束语

本文基于仿真分析获得了舵机多应力条件下加速试验载荷剖面。舵机在加速试验载荷的作用下，会引起舵机薄弱环节的加速失效，并满足加速比≥5 的要求。得出结论如下：

1） 建立了温-湿-电耦合应力的数学模型，并结合有限元分析软件，得到舵机在不同载荷类型和量级下的应力响应结果，以及舵机的薄弱环节和各应力载荷工作极限，为多应力作用下器件典型失效与环境载荷的关联分析提供理论基础。

2） 制定了面向航天典型机电产品的多应力加速试验设计方法，采用单应力加速模型相乘构建多应力条件下的加速因子模型。再通过最小二乘法对温度-湿度-电应力综合加速模型进行曲线拟合，确定模型待定参数取值，实现试验加速比≥5。

3） 提出的定量化剖面设计方法可以替代以多次摸底试验建立加速试验剖面的工作模式，降低试验样件的大量消耗和减少试验周期，为后续舵机多应力加速试验的开展起到指导作用。