考虑轮轨蠕滑的高速列车制动非线性振动行为研究
鲁昌霖,王志伟,2,王 权,莫继良,2
(1.西南交通大学 摩擦学研究所,成都 610031;2.西南交通大学 牵引动力国家重点实验室,成都 610031)
0 引言
随着高速列车运行速度不断提高、运行环境越发复杂,制动系统的安全性问题被广泛关注。盘式制动是高速列车制动系统中常用的制动方式之一,然而制动时盘片摩擦会诱发不稳定振动,不仅会引起制动夹钳断裂失效、制动闸片结构损伤和制动盘寿命缩短[1-3],还会导致严重的噪声问题[4-6],如由模态耦合振动引起的制动尖叫[7-8]和由于粘滑振动引起的蠕变呻吟[9]。因此,亟需开展高速列车盘式制动系统摩擦振动机理和抑制不稳定振动方法的研究。
国内外学者对制动系统的摩擦振动开展了大量试验研究,并通过建立制动系统相关数学模型,探究了制动装置系统参数、制动条件、制动摩擦界面特征等因素对制动系统摩擦学及动力学行为的影响。张康智等[10]关于制动盘、制动夹钳和闸片等物理特性方面的研究结果表明,降低制动夹钳的弹性模量,有利于降低制动系统的摩擦振动幅值,抑制系统的振动主频;赵旖旎等[11]关于摩擦块与摩擦盘振动间耦合关系的研究结果表明,系统各向振动的幅值均随转速的减小而增加;王宇[12]关于制动系统盘片Stribeck摩擦的研究结果表明,制动压力的变化会使系统出现周期混沌交替振动现象;姚亚航等[13-14]关于制动盘转速和制动压力等外部条件的研究结果表明,制动盘转速和制动压力是影响系统振动的重要因素。
然而,上述研究中的制动系统模型大多仅包含制动装置而未考虑制动时轮轨的黏着关系。实际服役过程中,轮轨黏着会导致制动系统等高速列车关键子系统的振动行为更加复杂[15-16]。Wang等[17-18]采用双线性轮轨蠕滑模型探究了轮轨相互作用对制动系统的影响,结果表明,轮轨蠕滑会影响制动系统的稳定性,且在较大蠕滑率下制动闸片更容易发生粘滑振动。但是,所采用的轮轨蠕滑模型较为简单,不能准确地反映制动过程中制动系统的振动行为。
因此,为更加真实地再现盘式制动系统在制动过程中的动态响应,建立了考虑Polach轮轨蠕滑的高速列车盘式制动系统3自由度非线性动力学模型。该模型不仅考虑了轮轨黏着关系,而且所采用的轮轨蠕滑模型能够更加准确地反映轮轨相互作用对制动系统的影响。基于该模型,进一步研究了低速制动时初始蠕滑率和轨面条件等轮轨黏着特征对制动系统非线性动力学行为的影响,并揭示了轮轨黏着与制动系统相互作用机理。研究结果可为高速列车盘式制动系统振动机理和控制方法提供参考和理论依据。
1 盘式制动系统动力学模型
1.1 动力学模型
简化的盘式制动系统模型见图1。假设:① 制动闸片简化为一个集中质量块;② 每个制动盘两侧制动闸片的物理参数和运动状态同步;③ 安装于同一轮对上的所有制动盘物理参数和运动状态同步;④ 轮对与制动盘的连接采用等效刚度与等效阻尼代替;⑤ 轮轨处于理想平衡位置,即车轮与钢轨的接触坐标系重合。
根据该假设,盘式制动系统被简化成一个3自由度的动力学模型,3个自由度分别为制动闸片的垂向运动、轮对的扭转运动和制动盘的扭转运动。根据牛顿第二定理,该动力学模型的运动方程可以描述为
(1)
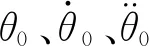
制动盘与闸片之间的摩擦力ff和总摩擦力矩Tf可通过盘片Stribeck摩擦模型获得;轮轨间动态黏着力矩Tb可通过Polach轮轨蠕滑模型获得。
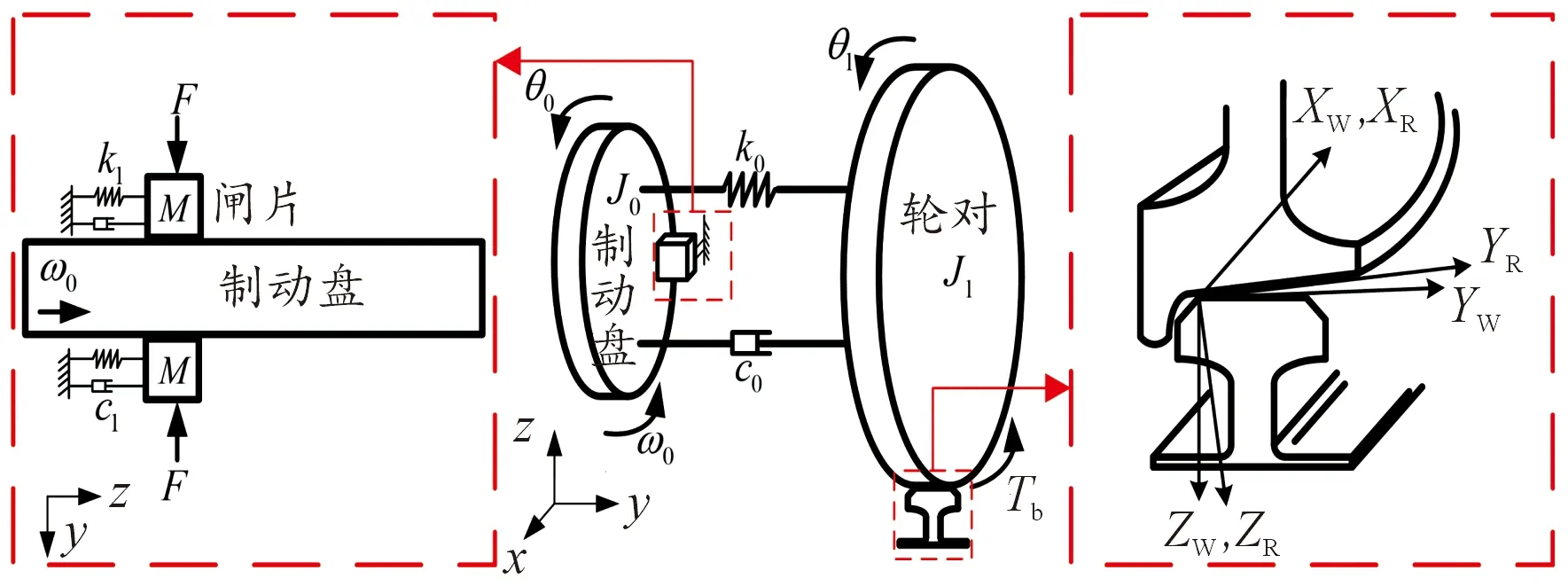
图1 简化的盘式制动系统模型
1.2 盘片Stribeck摩擦模型
Stribeck摩擦也称为Stribeck效应,主要用来描述低速区的摩擦行为,其模型能够很好地反应制动系统在相对低速下盘片之间的静摩擦与动摩擦之间的连续转换。盘片摩擦模型选用指数型Stribeck摩擦模型(如图2所示),摩擦因数定义为具有负斜率的相对速度的函数。摩擦因数与相对速度之间的关系表示为
μ(vr)=[μk+(μs-μk)e-α|vr|]tanh(βvr)
(2)
式中:μs和μk分别为静摩擦因数和动摩擦因数;α为控制负斜率程度的指数衰减系数;β为平滑参数;vr为制动盘和制动闸片之间的相对速度,其计算公式为
(3)
式中:ω为制动盘总的转速;ω0为制动盘的平均转速;r为制动闸片几何中心到制动盘转动中心的距离。
F为施加在制动闸片上的制动压力。制动盘与闸片之间的摩擦力ff和总摩擦力矩Tf可表示为
ff=F·μ(vr)
(4)
Tf=6rff
(5)
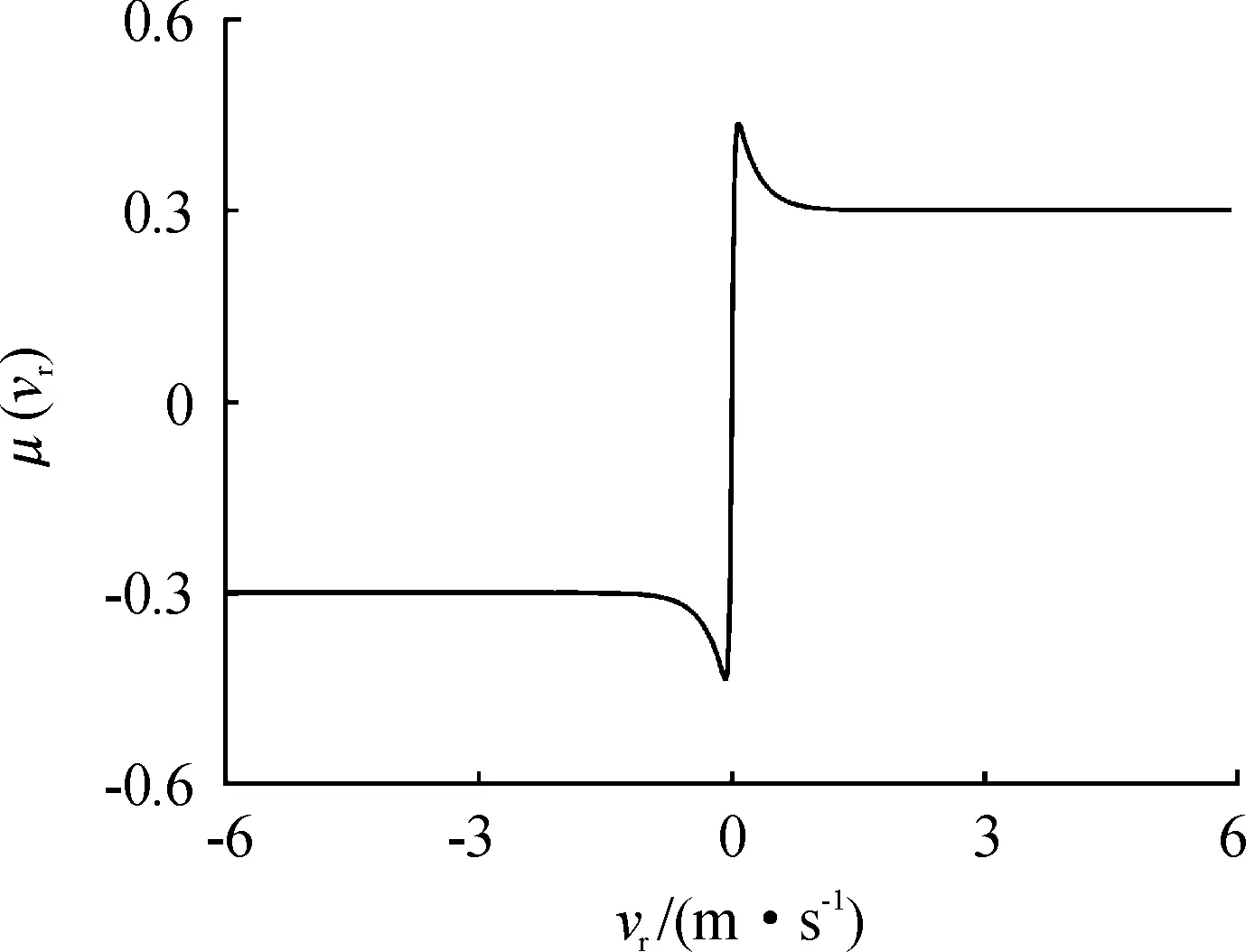
图2 Stribeck摩擦模型曲线
1.3 Polach轮轨蠕滑模型
Polach滚动接触理论,是在Kalker简化理论的基础上,与蠕滑有关的摩擦模型。该方法的优点是考虑了摩擦因数随蠕滑率的变化,且数值仿真精度较高、速度较快。Polach静态蠕滑力fb0和总蠕滑力fb1可由下式计算:
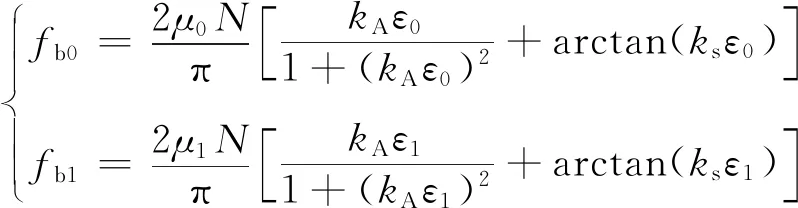
(6)
式中:N为轮轨正压力;kA和ks分别为Kalker系数在黏着区域和滑动区域内的衰减因子;ε0和ε1分别为静态缩减因子和动态缩减因子,如式(7)所示;μ0和μ1分别为轮轨静态摩擦因数和轮轨总摩擦因数,如式(8)所示。
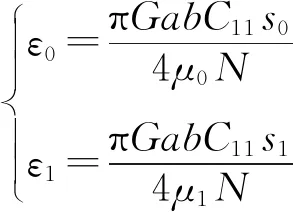
(7)
式中:G为剪切模量;a,b分别为接触斑的长短半轴,接触斑大小采用Hertz接触算法计算,由式(9)、(10)、(11)和(12)得到;C11为Kalker蠕滑系数,通过接触斑长短半轴之比查表可得[19],由假设(5)推导可知,接触斑长短半轴之比不变,得到所建立的模型中C11为定值;s0和s1分别为平均蠕滑率和动态蠕滑率,由于所建立的制动系统只考虑纵向蠕滑,且忽略了车轮纵向移动速度的变化和车轮滚动半径的变化,则s0和s1可通过式(13)和(14)计算得到。
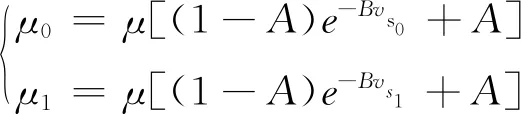
(8)
式中:A为蠕滑无穷大时对应的摩擦因数与最大摩擦因数之比;B为摩擦力指数衰减系数;μ为轮轨黏着摩擦因数。vs1和vs0分别为总的滑移速度和静态滑移速度,如式(13)所示。
(9)
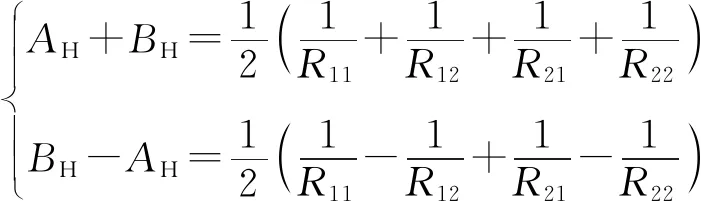
(10)
(11)
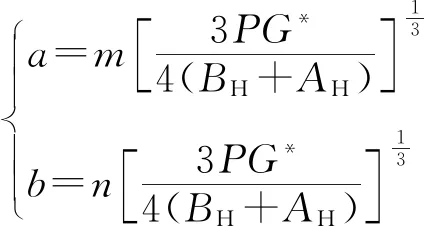
(12)
式中:P为轮对单侧轮轨接触法向力;G*为材料物理参数,由式(9)计算得到,ν1、ν2和Ε1、Ε2分别为轮轨的泊松比和弹性模量;AH、BH为Hertz接触计算参数,由式(10)计算可得,1/R11、1/R12和1/R21、1/R22分别为车轮和钢轨在接触坐标系原点处沿纵向、横向的主曲率;m、n是与η有关的椭圆积分,其值由式(11)计算出角度参数η后通过查表得到[20]。
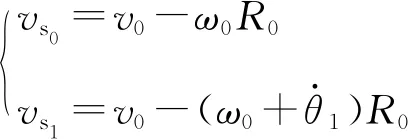
(13)

(14)
式(14)中,v0为车轮纵向的平均移动速度;vs0和vs1分别为轮轨纵向平均相对速度和总的相对速度,可由式(13)计算得到,ω0为车轮滚动的平均角速度,R0为车轮名义滚动半径。
最终,通过式(6)—(14)可计算出Polach静态蠕滑力fb0和总蠕滑力fb1,则轮对与轨道间动态黏着力矩Tb为
Tb=2(fb1-fb0)R0
(15)
2 现场试验
利用在京沪高速铁路上线路试验的结果,验证制动系统非线性动力学模型的正确性。试验中,由于在制动夹钳和制动闸片上安装传感器较为困难,因此,将传感器(采样频率为5 000 Hz)安装在制动夹钳座附近,用于测量垂向振动加速度,如图3所示。
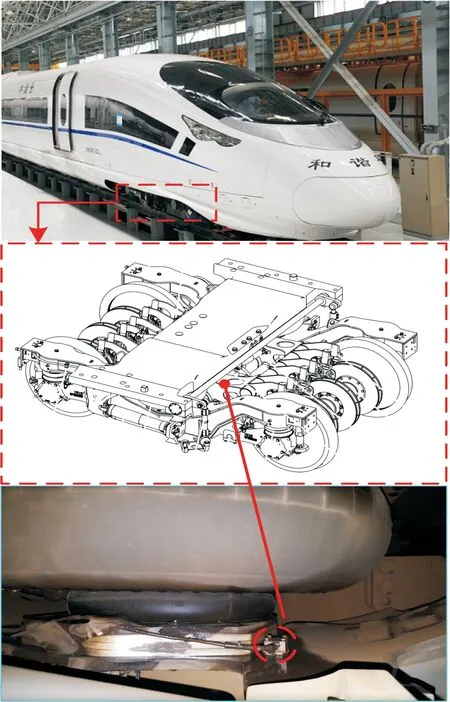
图3 线路试验传感器安装位置示意图
图4(a)是线路试验中采集的制动工况下闸片振动加速度时域图。车辆初始运行速度为350 km/h,在260 s时开始施加制动,车辆速度在500 s时降低至0 km/h。可以发现,振动加速度在制动开始后逐渐减小,但在车辆停止前的相对低速段内(0~35 km/h),振动加速度急剧增加,并出现较大幅值的振荡。结果表明,车辆在相对低速下制动时出现了更为剧烈的不稳定振动。
进一步,对前文所建立的动力学模型进行数值仿真,得到制动闸片在车速为5、40 km/h工况下制动时的振动加速度时域信号,结果如图4(b)所示。可以发现,制动闸片在车速为40 km/h时振动较小,在车速为5 km/h时振动十分剧烈。结果表明,在相对低速下制动时,制动闸片出现了较大幅值的不稳定振动,这与线路试验结果变化趋势一致。因此,所建立的动力学模型能够有效反映高速列车服役过程中制动系统的振动特性,可用于低速制动工况下盘式制动系统非线性振动行为的研究。
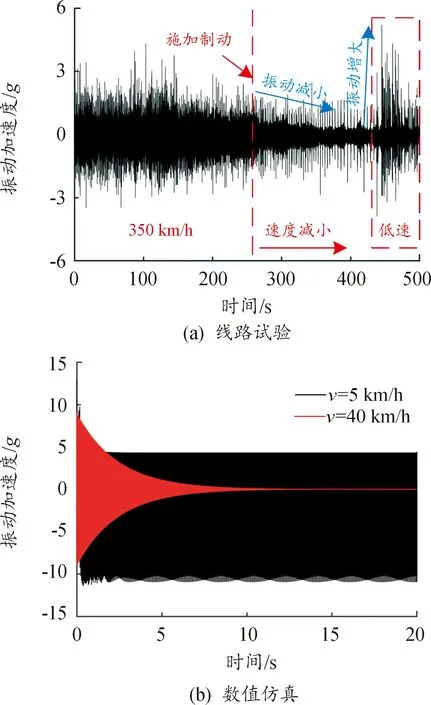
图4 线路试验与数值仿真的制动闸片振动结果
3 数值仿真结果分析及讨论
仿真过程中,制动系统主要性能参数与文献[17]一致,相关轮轨参数如表1所示。对比分析Polach轮轨蠕滑模型与双线性轮轨蠕滑模型的差异,研究平均蠕滑率和轨面条件对制动系统振动行为的影响规律,讨论轮轨黏着与盘式制动系统非线性行为的相互作用机理。
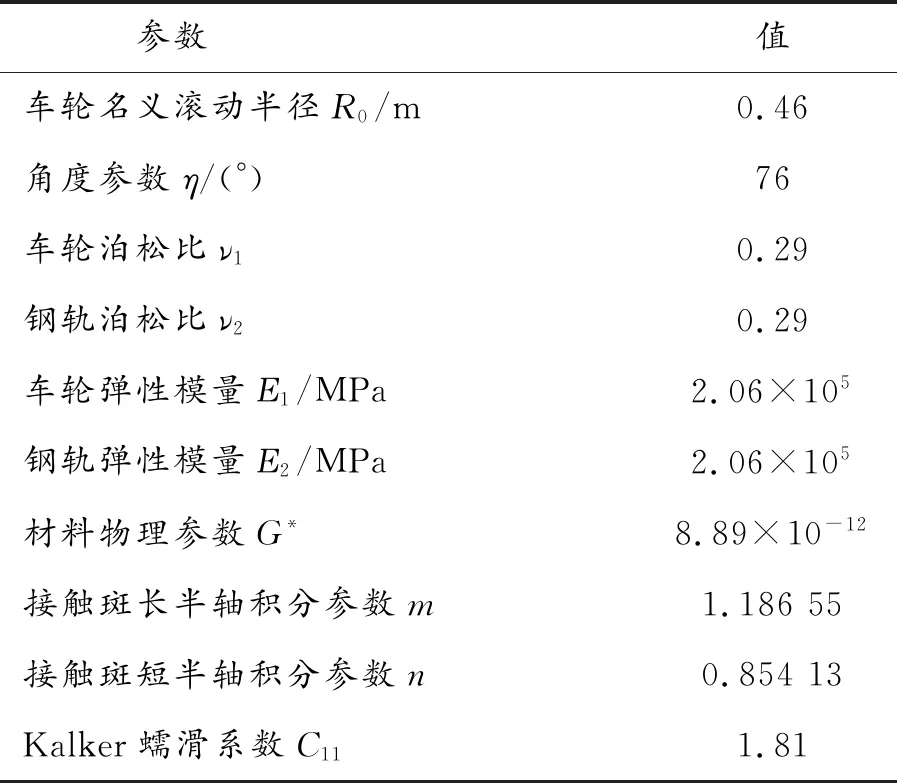
表1 轮轨参数
3.1 Polach与双线性轮轨蠕滑模型对比
轮轨蠕滑力的计算与轮轨蠕滑模型密切相关。双线性轮轨蠕滑模型作为常见的轮轨蠕滑模型之一,由于其线性特性,便于系统线性化处理及稳定性分析,但用于反映实际轮轨蠕滑特性过于简化,进而也不能较为真实地反映轮轨黏着对制动系统的影响。因此,采用Polach轮轨蠕滑模型与双线性轮轨蠕滑模型进行对比分析,以说明两者在反映制动系统动态特性方面的差异。
通过Polach接触理论,可以得到不同车速下轮轨纵向蠕滑力与纵向蠕滑率的变化关系,如图5(a)所示。结果表明,Polach轮轨蠕滑模型与双线性轮轨蠕滑模型(见图5(b))相比有明显差异,双线性轮轨蠕滑模型与车速变化无关,然而,Polach轮轨蠕滑模型受车速影响较大。
为了对比低速下Polach轮轨蠕滑模型与双线性轮轨蠕滑模型对盘式制动系统的影响,分别进行数值仿真。仿真过程中,系统参数与文献[17]相同,计算结果如图6所示。
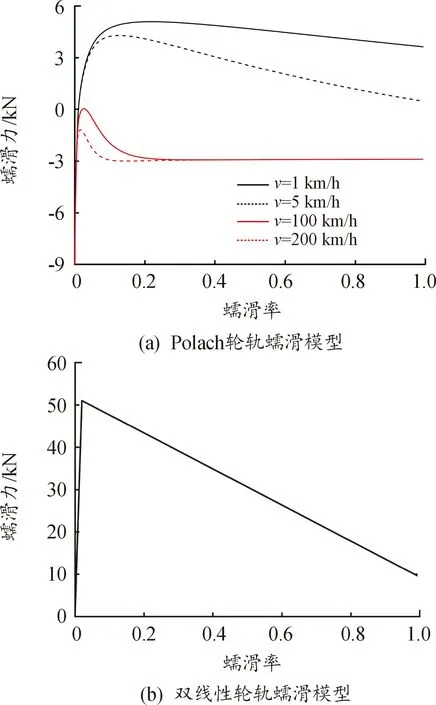
图5 轮轨蠕滑模型
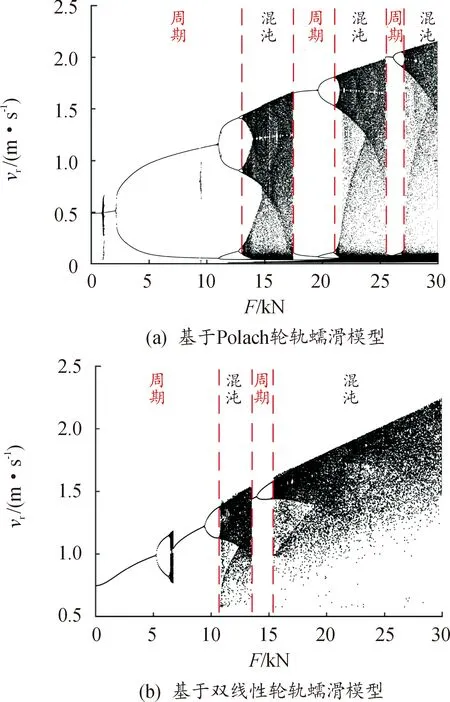
图6 基于2种轮轨蠕滑模型的制动闸片振动行为
结果表明,基于2种蠕滑模型的制动系统闸片单元均出现周期振动和混沌振动交替的现象,且随着制动压力的增大,混沌振动区域增大,周期振动区域减小;然而不同的是,基于Polach轮轨蠕滑模型的制动系统闸片单元出现混沌振动时的制动压力更大,且对应周期振动区域的范围更大。
3.2 平均蠕滑率对制动系统的影响
平均蠕滑率常用来描述轮轨静态的接触状态[21]。为了对比低速时不同蠕滑率工况下,制动压力对盘式制动系统动态振动的影响,进行数值仿真分析。仿真过程中,设置平均转速为1 rad/s,轴质量为17 t,轨面为干燥状态,平均蠕滑率s0分别设置为0.001和0.01,计算结果如图7所示。
图7中(a)和(b)分别为s0=0.001和s0=0.01工况下制动系统闸片单元受制动压力影响的分岔图。结果表明,2种工况下制动闸片均出现周期振动和混沌振动交替的现象。相比于s0=0.001工况,当s0=0.01时,制动闸片出现混沌运动时的制动压力更小,周期运动区域更窄;此外,在相同制动压力区间内,s0=0.01时更容易出现车轮抱死的情况,严重影响车辆制动安全性。因此,较大的平均蠕滑率可能导致制动系统更不稳定。
为了进一步对比相同制动压力下,不同平均蠕滑率对制动系统的影响,采用相平面进行分析,结果如图8所示。不难看出,制动压力为21 kN时,在s0=0.001工况下的制动闸片为单周期stick-slip振动,制动盘和轮对都为三周期扭转振动。而在s0=0.01工况下,制动闸片、制动盘和轮对均为多周期混沌振动。
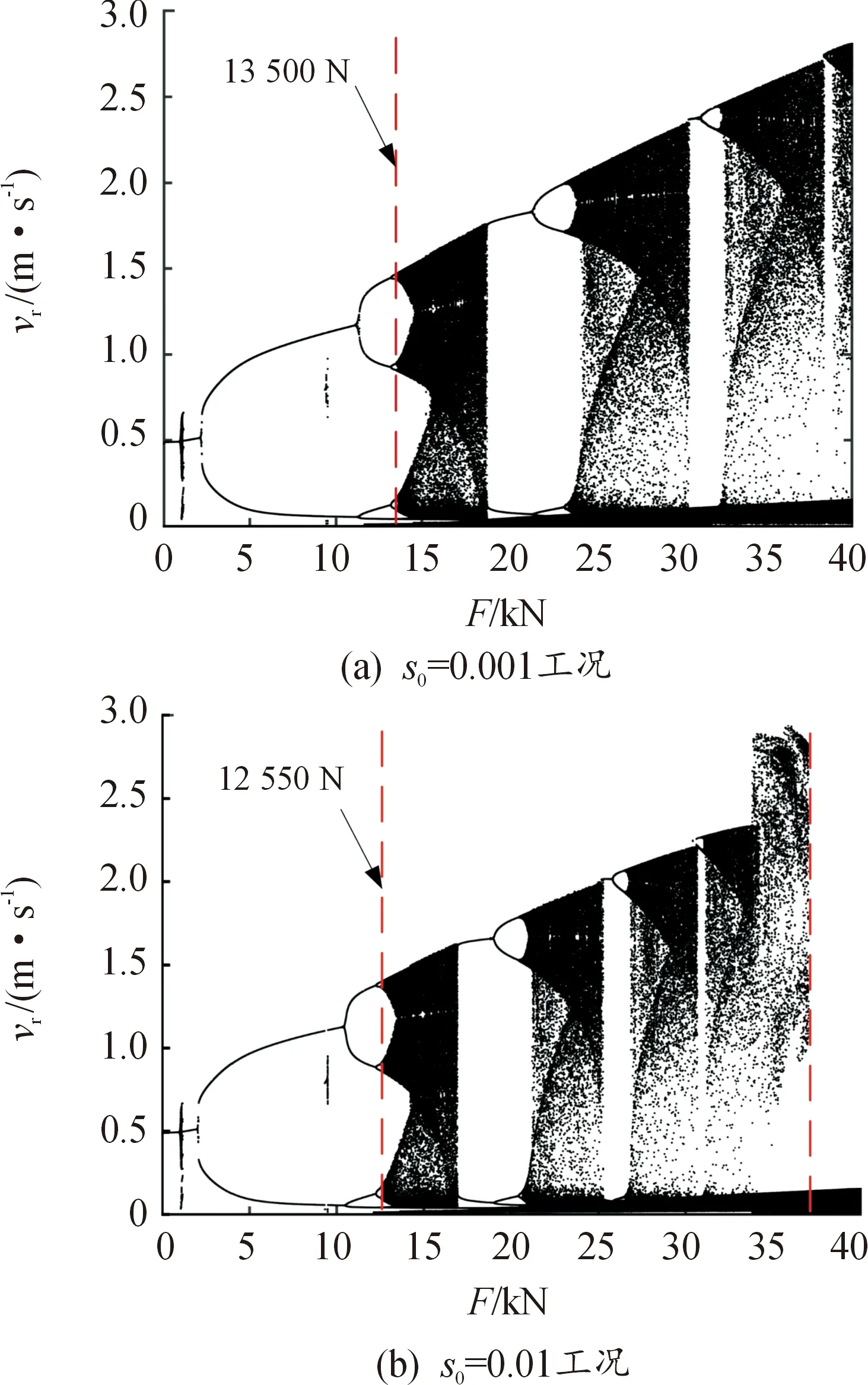
图7 不同平均蠕滑率工况下制动闸片受制动压力变化的振动行为
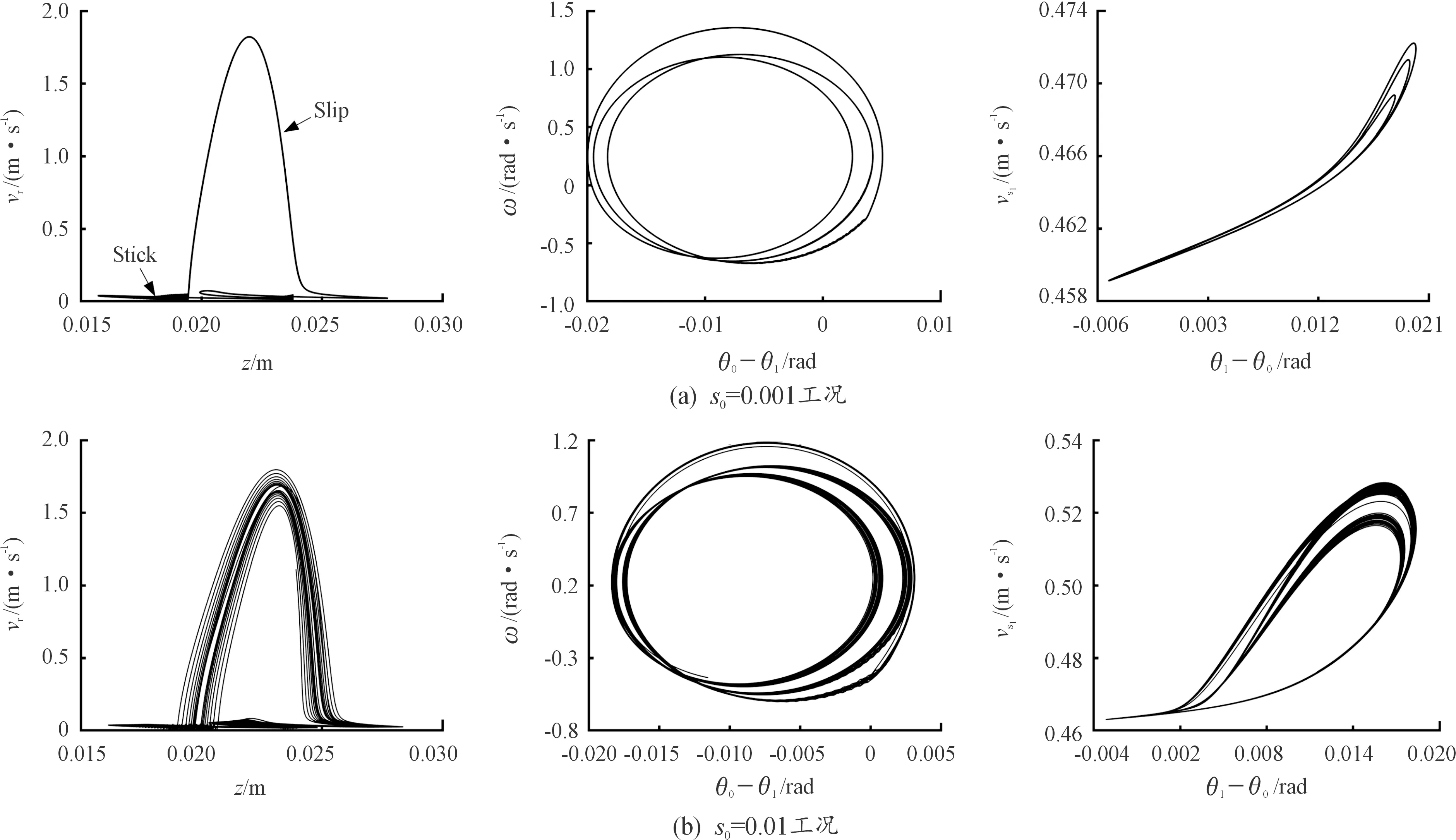
图8 不同平均蠕滑率下制动压力为21 kN时制动系统的相平面图
制动系统不仅受制动压力的影响,还受车辆行驶速度的影响[14]。因此,通过仿真分析研究不同平均蠕滑率工况下,车速对制动系统振动行为的影响规律。仿真过程中,设置制动压力为常用制动压力18 kN,轴质量为17 t,轨面为干燥状态,平均蠕滑率s0分别设置为0.001和0.01。计算结果如图9所示。
图9中(a)和(b)分别为s0=0.001和s0=0.01工况下制动系统闸片单元受车速影响的分岔图。结果表明,2种工况下的制动闸片均在低速下发生剧烈振动,与现场试验的结果一致;2种工况下的制动闸片临界车速不同,分别为8.6 km/h和6.3 km/h。因此,平均蠕滑率会影响制动闸片的临界车速。

图9 不同平均蠕滑率下受车速影响的制动闸片振动行为
3.3 轨面条件变化对制动系统的影响
轨面条件在车辆行驶过程中随时有可能发生变化。通过Polach蠕滑理论公式可以得到低速(ω0=1 rad/s)工况不同轨面条件下纵向蠕滑力与蠕滑率的对应关系(如图10所示)。不难发现,轮轨黏着受轨面条件影响较大,因此,轨面条件对制动系统的影响也要加以考虑。
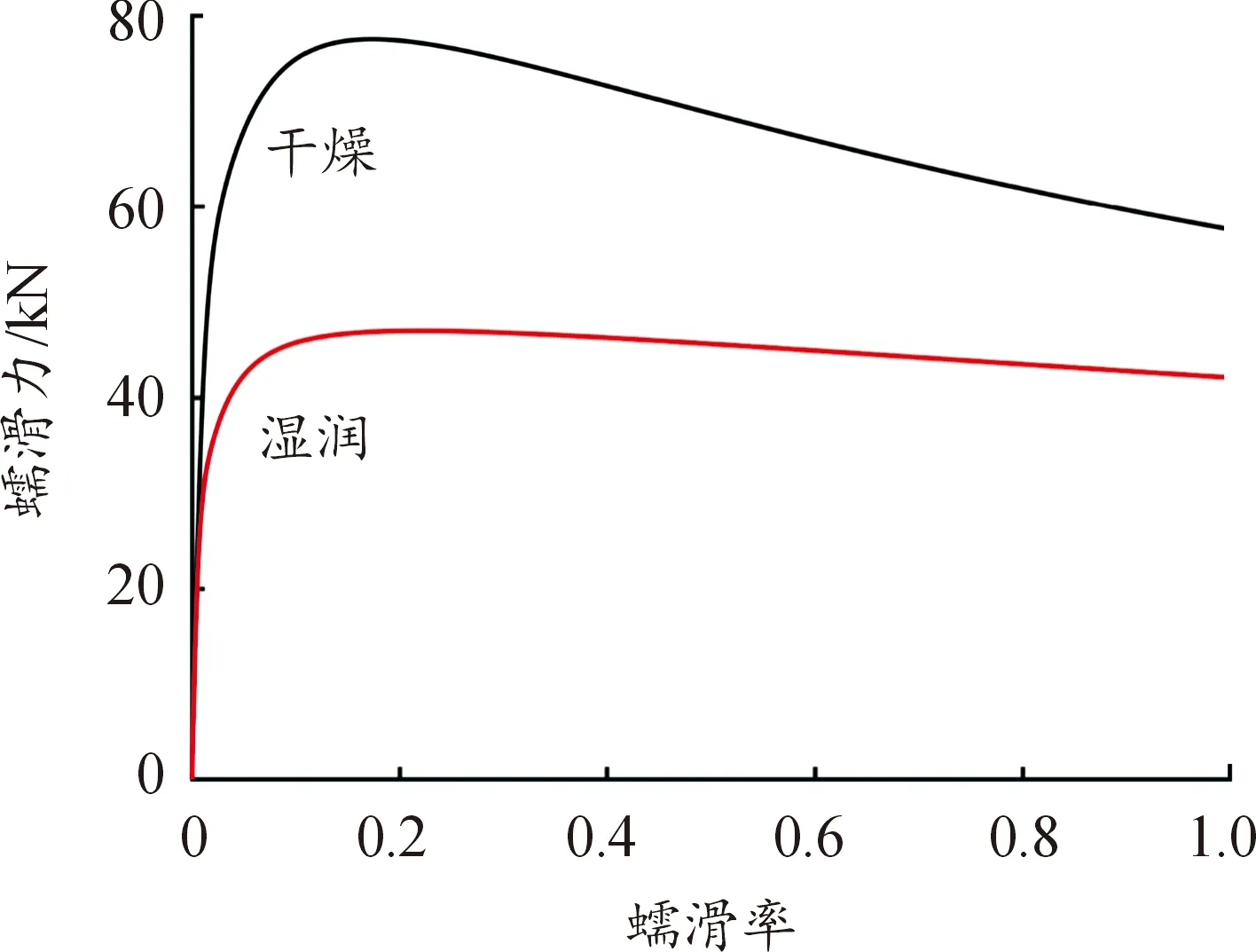
图10 Polach摩擦模型
为了对比不同轨面条件下盘式制动系统受制动压力影响的振动响应,进行仿真分析。仿真过程中,设置平均转速为1 rad/s、轴质量为17 t、平均蠕滑率为0.001,轨面条件分别设置为干燥和湿润(详细参数见表2[22])。计算结果如图11所示。

表2 参数设置

图11 不同轨面条件下制动闸片的振动行为
图11中的(a)和(b)分别为湿润和干燥轨面条件下制动系统闸片单元受制动压力影响的分岔图。结果表明:相对于干燥轨面,湿润轨面下的制动闸片出现混沌振动时所对应的制动压力更小,混沌区域和周期区域交替出现的次数增加,且对应周期区域更小。因此,湿润轨面会导致制动系统更不稳定。
3.4 讨论
轮轨接触与制动系统非线性行为相互作用机制如图12所示。基于前文分析可知,轮轨黏着状态受平均蠕滑率和轨面条件影响较大。平均蠕滑率是制动时的初始蠕滑情况,进而直接影响轮轨蠕滑力的大小;轨面条件决定了轮轨摩擦因数的上限,直接影响蠕滑力大小的变化。平均蠕滑率和轨面条件均直接影响Polach轮轨黏着-蠕滑特性,然后通过蠕滑力的传递与振动影响轮盘扭转,进而导致制动盘的振动形式发生变化,再通过盘片摩擦导致制动闸片切向的受力情况发生变化,最终影响制动系统闸片的非线性振动行为。此外,车速和制动压力的变化直接对制动单元的非线性振动行为产生影响。
同理,制动闸片的非线性行为通过盘片摩擦和轮盘扭转影响轮轨的相对滑移情况,最终影响轮轨黏着状态。
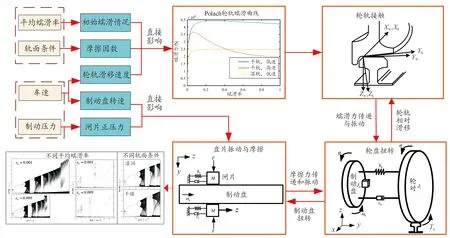
图12 轮轨黏着与盘式制动系统的相互作用机制
4 结论
建立考虑Polach轮轨蠕滑的高速列车盘式制动系统非线性动力学模型,并通过与现场试验数据对比验证模型的正确性。基于该模型,对比了Polach与双线性轮轨蠕滑模型的差异,研究了低速下平均蠕滑率和轨面条件对盘式制动系统非线性振动行为的影响规律,讨论了轮轨黏着与盘式制动系统非线性振动行为的相互作用机理。结果表明:
1) 在相对低速情况下,数值仿真与现场试验结果均表明制动系统出现了异常振动,系统的稳定性较差。
2) 相比于双线性轮轨蠕滑模型,采用的Polach轮轨蠕滑模型更能体现轮轨黏着随车速的变化,轮轨蠕滑力的变化也更为平滑。此外,基于Polach轮轨蠕滑模型的盘式制动系统非线性振动行为更为丰富,也更加符合实际服役情况。
3) 平均蠕滑率增大、轨面条件变差均会导致高速列车盘式制动系统的非线性振动行为更加复杂,影响系统的稳定性。

