数学核心素养测评之情境领域分析

胡典顺 李姿颖

胡典顺 华中师范大学数学与统计学学院教授、博士研究生导师，华中师范大学数学教育教研室主任，湖北省中学数学教学指导委员会副主任委员；《数学教育学报》《数学通讯》编委，鄂教版高中数学教材（2019年版）副主编，中国国际文化交流基金会第三届“明德教师奖”获得者；曾以访问学者的身份，由国家留学基金委公派访问美国特拉华大学；在《课程·教材·教法》《中国教育学刊》《数学教育学报》《教育科学研究》等期刊上发表论文270余篇，出版《基于数学意义的数学教学改革研究》《整合技术的学科教学知识：从教师专业素养到教师教学实践》《中学生数学素养测评的模型建构与实证研究》等专著，主持多项全国教育科学规划项目和教育部人文社会科学研究规划基金项目。

数学核心素养的测评主要从内容领域、情境领域、过程领域、核心素养领域四个维度展开。情境领域主要考查学生从具体情境中抽象出数学问题的能力，是学生“会用数学的眼光观察现实世界”的重要体现，是数学核心素养测评的重要一环。本文就“WJ市义务教育核心素养监测”项目阐述数学核心素养测评中情境领域试题的设计思路，论述测评数据的分析方法及结果。

一、试题情境的设计思路

数学核心素养表现为学生在各种情境下表征、运用和阐述数学的能力。数学情境是数学知识与现实生活联系的媒介，也是数学问题提出的前提。因此，数学核心素养的测评离不开情境，好的情境能保证测评结果的真实性和准确性。

国际PISA数学测试为数学核心素养的测评提供了重要参考：在情境领域，2021年PISA数学测试将数学情境划分为个人情境、职业情境、社会情境、科学情境四类，涉及学生的个人生活、社会生活、教育和职业发展等方面，基本覆盖了现实生活中常见的情境，有利于学生在熟悉的情境中从数学的角度发现和提出问题，拓宽学生的视野。因此，本项目中数学试题的情境类型同样按此分为四类。

为了给教师改进教学提供有力参考，笔者结合《义务教育数学课程标准（2022年版）》要求和国际测评经验，提出好情境要满足的几个原则：①认知接近性原则，即情境创设要关注学生身邊发生的事情，从社会生活、科学和学生已有的数学经验等方面入手，选择贴近学生生活经验、符合学生年龄特点和认知特点的素材；②真实性原则，即情境材料要来源于生活实践，相关数据要真实可靠，不出现争议性话题；③启发性原则，即试题情境应层层递进，启发学生逐步深入探究；④多样性原则，即一套数学核心素养测试卷应涉及多种情境，且比重恰当。

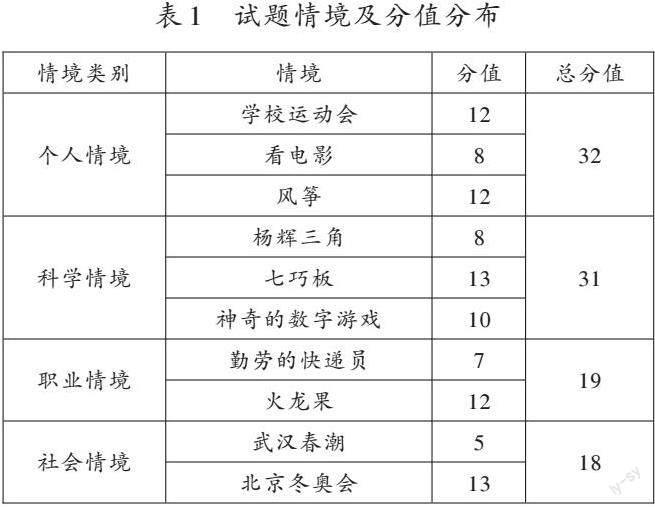
在本项目的小学试题情境设计过程中，笔者结合具体学情和数学课程内容，将试题中个人情境、科学情境、职业情境、社会情境的题目分值占比分别设置为32%、31%、19%、18%。具体的试题情境及分值分布如表1所示。

下面，笔者以“武汉春潮”试题为例，做具体说明。

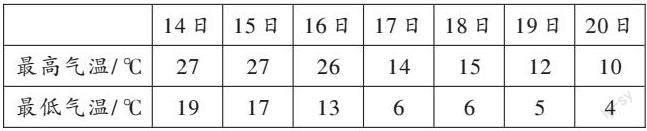
对于“倒春寒”，2018年5月1日开始实施的《倒春寒气象指标》这样定义：倒春寒，一般是指每年春季（3～5月）出现的前期暖、后期冷且后期气温明显低于正常年份气温的现象。本轮3月寒潮过程中，武汉降温幅度为8℃至11℃，省内局部有短时强降水、雷电大风等强对流天气，阵风8级。下表为2022年3月14日至3月20日武汉市气温纪录。

问题1 请你根据上表中的数据，把条形统计图补充完整。

问题2 “温差”是一天当中最高温度和最低温度之差，请问这一周里哪天的温差最大？

该试题是一道社会情境的试题，属于第二学段的数学核心素养测评试题。其具体情境是“武汉春潮”，主要涉及气温的变化，是学生有实际感触的事情，符合认知接近性原则；情境材料来源于生活，数据来自武汉市气象局，符合真实性原则；两个问题层层递进，让学生从依托条形统计图直观感知每天的温差到通过计算判断哪一天温差最大，顺应学生的思维逻辑，符合启发性原则。

二、测评数据的分析方法及结果

在得到测评数据后，我们可以通过学生的分项表现，以及达标学生、卓越学生的比例，研究学生在不同情境领域的能力表现；通过相关性分析，研究学生作答不同情境题目的表现之间的内在联系；通过差异性分析，研究影响学生情境领域能力表现的相关因素。具体分析方法如下。

1.能力分数分析

学生从具体情境中抽象出数学问题的能力在测评中的直接表现是学生作答不同情境题目的得分。由于不同情境的题目在测试卷中的分值占比不同，笔者将学生作答四种情境题目的成绩加权成100分，取加权后的分数作为学生作答四种情境题目的能力分数。下面，笔者以个人情境为例，阐述能力分数的计算过程。

本测试卷中，个人情境的题目有3道，分别为“学校运动会”“看电影”“风筝”。若学生A作答3道题目的得分分别为10分、6分、8分，则学生A在个人情境的得分为24分。由于个人情境在该测试卷中的总分值为32分，所以学生A的个人情境能力分数为“24[÷]32[×]100=75”分。笔者取WJ市所有学生的个人情境能力分数的平均值，作为WJ市学生的个人情境能力分数；取WJ市学生的四种情境能力分数的平均值，作为WJ市学生的情境领域能力分数。

学生取得的不同情境的能力分数体现了学生解决不同情境问题的能力，分析能力分数，能帮助我们找到学生擅长的或有待提高的情境领域。笔者基于3544份有效数据，计算WJ市学生取得的四种情境试题的能力分数（精确到百分位）：个人情境能力分数为73.38分，科学情境能力分数为76.49分，职业情境能力分数为83.90分，社会情境能力分数为59.71分。这说明学生在职业情境题目的作答中表现最好，在个人情境和科学情境题目的作答中表现良好，但作答社会情境的题目有一定的困难。教师应该在日常教学中注重创设社会情境的数学问题，促进学生数学核心素养的全面发展。

2.精熟度水平分析

为了清晰表征学生的数学核心素养水平，分析学生是否具备满足其日后生活、就业和进一步学习所需的基本数学能力，PISA数学测试引入精熟度水平概念，以此描绘学生的数学核心素养所处的层次。其中，2级为基础水平，达到基础水平的学生被视为掌握了适应未来社会所需的基本数学能力；5级、6级为高水平，达到高水平的学生占比可以在一定程度上反映国家未来人才的储备量。

根据国际学生评估项目中国上海项目组划分精熟度水平等级的方法，基于本项目的3544份数据，笔者计算得出学生数学精熟度水平分布情况，并绘制四种情境领域学生精熟度水平分布百分比条形图（见图1）。

由图1可知，在个人情境、科学情境、职业情境、社会情境未达到基础水平（2级精熟度水平）的学生占比分别为7.9%、8.9%、8.1%、8.1%；达到高水平（5级、6级精熟度水平）的学生占比分别为47.8%、40.8%、48.7%、38.3%。

为了更好地分析学生作答四种情境领域题目的能力表现之间的差异，笔者绘制了如图2所示的未达到基础水平的学生和达到高水平的学生占比折线图。

由图2可知，在科学情境未达到基础水平的学生占比最高。对部分学生而言，科学情境最陌生，亲身体验的机会较少，因而在建构问题情境与数学知识之间的联系时比较困难。在社会情境达到高水平的学生占比最低，且能力分数均值较低，说明大部分学生在解决社会情境的数学问题时不够熟练，需要加强练习。在个人情境未达到基础水平的学生占比最低，达到高水平的学生占比较高，说明学生在个人情境题目的作答中表现良好。学生作答职业情境试题的表现最好，无论是能力分数均值还是高水平学生的占比，都是最高的，说明学生能够较好地解决以职业情境为背景的数学问题。

3.达标学生与卓越学生占比

学生作答某种情境题目的表现达到基础水平，可以说明学生能够运用数学知识顺利解决某种情境的现实问题，但不足以说明学生具备了基本的数学核心素养。只有学生作答四种情境题目的表现都达到基础水平，才能说明学生在数学核心素养情境领域的表现达标。本测评将这类学生视为达标学生。笔者运用SPSS26.0筛选达标学生，具体步骤为：点击【数据】[→]【选择个案】[→]【如果条件满足】，在数学表达式中输入“GR[>=]51.8&KX[>=]54.5&ZY[>=]65.1&SH[>=]25.2”（“GR”表示个人情境，“KX”表示科学情境，“ZY”表示职业情境，“SH”表示社会情境），点击【继续】[→]【确定】。由此得出：在情境领域表现达标的学生有2806人，占比79.2%。这一结果表明WJ市的基础教育能保证大部分学生达到基本能力要求。

在前面的分析中，我们可以看出，作答个人情境、科学情境、职业情境、社会情境题目的表现达到高水平的学生比例均在35%以上，占比较高，但学生在某一种情境表现优异，不足以说明学生在所有情境都表现优异。本项目将在四种情境领域的表现均达到高水平的学生视为卓越学生。笔者运用SPSS26.0筛选得到卓越学生有403人，占比11.4%。这说明作答某种情境题目的表现达到高水平的学生中，很大一部分学生不能在所有情境都达到高水平，也就是说，在情境领域全面发展的卓越学生占比较少。

4.相关性分析和差异性分析

与数学核心素养测评内容领域的分析类似，我们可以就情境领域，对学生在个人情境、科学情境、职业情境、社会情境四个分量的表现进行相关性分析，发现其内在联系。

笔者运用SPSS26.0计算四个分量两两之间的皮尔逊相关系数，得到表2。

由表2可知，个人情境、科学情境、职业情境、社会情境之间都具有相关性，我们可以认为：四种情境中，学生作答任意一种情境题目的表现都会影响其作答其他情境题目的表现。这体现了数学学科的整体性，若教师没能培养好学生运用数学知識解决某种情境领域问题的能力，则学生作答其他情境领域题目的表现也会受到影响。因此，教师在教学工作中应该重视不同情境之间的联系，尽量设置符合学生认知实际且兼顾两个及两个以上情境类别的问题，以促进学生数学核心素养的全面发展。

我们也可以就情境领域进行差异性分析，明确不同举办者类型、不同办学类型、学校所处位置等因素是否影响学生在情境领域的表现。对于两组数据的差异性分析，一般通过独立样本t检验进行；对于三组及三组以上数据的差异性分析，则要使用方差分析及S-N-K、LSD等多重比较分析。笔者以“学校所处位置（城市、县镇、乡村）对学生在情境领域的表现是否具有显著差异”的研究为例，对如何利用SPSS26.0进行三组及三组以上数据的差异性分析做介绍。

建构数据文件后，笔者首先进行描述性统计，以此做初步判断。统计结果显示：城市学校学生得分均值为74.471分，县镇学校学生得分均值为71.329分，乡村学校学生得分均值为73.461分，三者有一定的差异。为确定差异是否显著，笔者利用SPSS26.0做进一步验证，具体步骤为：①点击【分析】[→]【比较平均值】[→]【单因素ANOVA检验】，将“情境领域能力分数”放入【因变量列表】对话框，将“学校位置”放入【因子】对话框；②点击【事后比较】，选择【S-N-K】，点击【选项】，选择【描述】，点击【继续】[→]【确定】。运行结果如表3、表4所示。

由表3可知，组间F值为12.121，显著性P值小于0.05，则拒绝原假设，表明学校所处位置的不同对学生在情境领域的成绩有影响，处于不同位置的学校学生成绩之间存在显著性差异。观察表4，我们可以发现，学校所处位置分为2个子集，县镇学校在子集1中，乡村学校和城市学校在子集2中，差异发生在子集之间，同一子集中的学校位置之间不存在显著性差异，也就是说，乡村学校的学生与城市学校的学生在情境领域的表现无显著差异；县镇学校的学生在情境领域的表现显著低于其他位置学校的学生。

（李姿颖系华中师范大学数学与统计学学院硕士研究生）

责任编辑 刘佳