家庭人均收入不平等测度方法的改进与实证

魏艳华，王丙参，，朱 琳

（1.天水师范学院 数学与统计学院，甘肃 天水 741001;2.首都经济贸易大学 统计学院，北京 100070）

0 引言

消减不公平现象需要对资源（家庭人均收入等）占有不平等程度进行测度[1—3]。目前，关于不平等测度（IEM）的文献有很多，已有研究[1—5]从不同角度对IEM进行探讨，给出了一些不平等指标（IEI）的使用范围、选择准则，但仍不够系统、深入。测度地区差异本质上就是度量不平等程度[6]，这方面的文献有很多，但选用的IEI可能不同，即使选用同一指标，计算公式也可能因个人习惯、数据特征而存在差异，这样得到的不平等程度可比性差、易混淆。另外，针对复杂数据结构，需要对已有IEI进行修正、拓展，甚至要构造新的IEI。中国家庭金融调查（CHFS）是对家庭金融行为的大型抽样调查，已有研究基于此数据产生了一系列有意义的结论[7]。中国家庭因血缘、人伦关系存在较强的资源内部转移现象，因此从家庭人均收入角度测度不平等程度更合理，但是家庭规模存在差异，这就需要将传统不平等指标（每个观测数据权重一样）推广到加权场合（每个家庭人均收入以家庭人数加权）。鉴于此，本文首先基于中国家庭人均收入、家庭规模，比较研究5种IEI并给出其计算公式、相互间的关系、适用范围；然后，将Gini系数、堪培拉指数推广到加权场合，给出不平等测度数值分解方法；最后，根据CHFS微观数据测度以家庭规模加权的家庭人均收入不平等程度。

1 不平等测度方法

1.1 变异系数（CV）

其中，μ=E(x)，Pi和P分别表示家庭人数与总体的平均家庭人数。IEI重点关注的是资源占有不平等程度以及取值如何随着资源改变而变化，而不仅是度量离散程度，因此它还需要满足一些基本性质（公理），比如齐次性等。假定观测值x1，…，xn表示家庭人均收入，对应家庭规模刻画其重要程度，这就需要采用加权IEI进行测算，比如加权CV。

1.2 泰尔指数

其中，Ik和nk分别是第k组指标取值和样本量，表示第k组指标占比。从式（1）来看，它可计算以家庭人数为权重的家庭人均收入不平等程度，即将一个家庭看作一个分组，类似组间T指数，可见，根据式（1）计算的分组T指数可以看作加权T指数，即Ik、nk分别表示第k个家庭的总收入、人口规模。若将样本xi(i=1，2，…，n)分为n组，则有：

1.3 Gini系数

1907 年，Lorenz 将收入x1，…，xn按升序排列，计算收入最低百分比（记作p）的人口所获得的收入百分比（记作，其中f(t)是概率密度函数），则由所有点(p，L(p))所组成的曲线称为Lorenz曲线（见图1）。L(p)越弯曲，收入分配越不平等，L(p)=p称为绝对平等线。绝对平等线与L(p)围成的区域A用来度量不平等，绝对不平等线（y=0，0 ≤p≤1与p=1，0 ≤y≤1组成的折线）与L(p)围成的区域记为B，通常将作为IEI，这也是Gini 系数的由来。Gini 系数与L(p)不是一一对应的，两个完全不同的收入分布可能会计算出相同的Gini系数。在计算Gini系数时，通常假定指标取值非负：

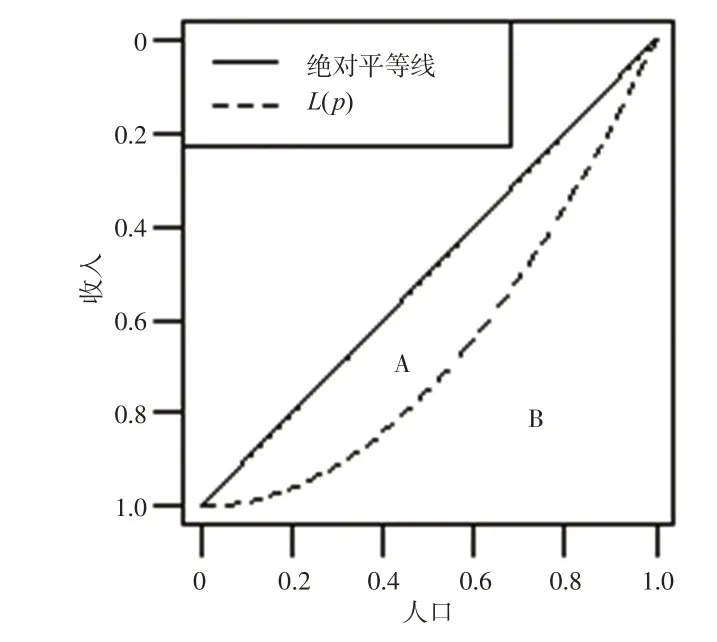
图1 Lorenz曲线

通常根据观测值x1，…，xn来计算Gini系数，即：

在现实中，每个观测值的重要性不同，假定x1，…，xn对应的权重依次为w1，…，wn，且满足w1+…+wn=n，则可定义加权Gini系数：

1.4 Canberra指数

如果个体具有相同收入，则μ=μi，p=L(p)，Canberra曲线与连接（0，0）和（1，0）的平等线重合，因此，C 指数就是Canberra曲线下方的面积：

1.5 Zenga指数

若将家庭人均收入定义为yi，r个家庭对应人数为n1，n2，…，nr，则可根据式（10）直接计算Zenga指数（简称Z指数）。显然，Z 指数适合计算考虑家庭人数情况的家庭人均收入不平等程度，也可称为加权Z指数。

Z指数的连续形式为：

其中，R称为交叉项，可计算Gini、T 等5 个指数的数值分解。当R≥0 时，交叉项称为正向交叉，增加不平等程度；反之，称为负向交叉。

1.6 不平等指数IEI的性质

不同IEI 及其分解的侧重点不同，表示的含义也有差别，需要合理解读。IEI 选择准则常取决于IEI 的性质，见表1。CV、T指数、Gini系数、C指数、Z指数简称五指标，依次称为指标1至指标5。

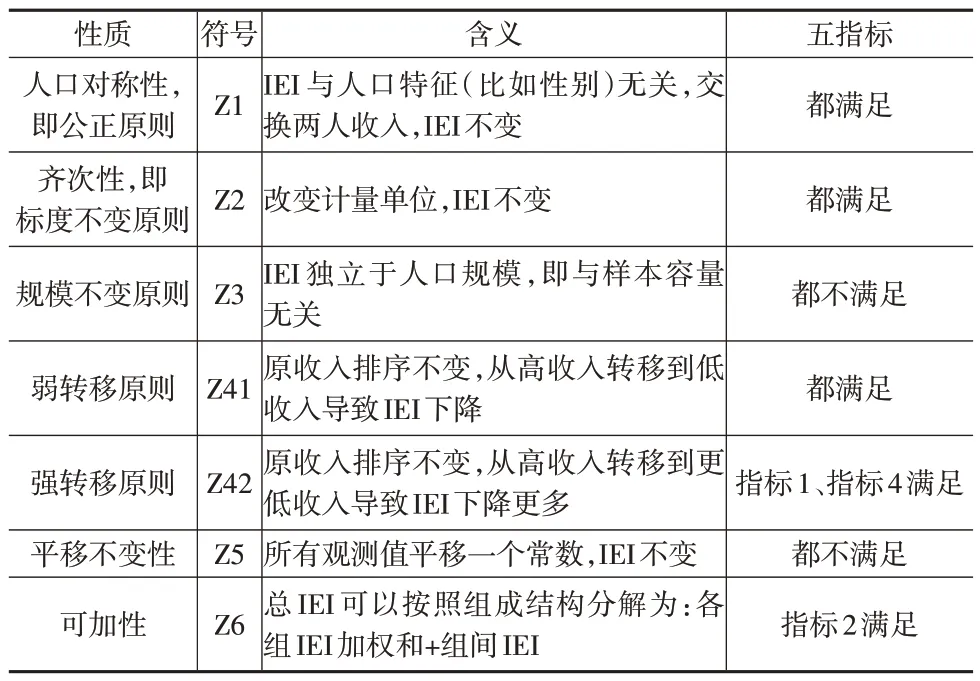
表1 IEI选择准则

公正原则（Z1）是最基本的性质，也是必要性质，只要IEI仅依赖观测数据本身，就会满足公正原则，可以认为不满足此原则的IEI是不合格的；齐次性（Z2）是不公平程度（即离散程度）可比的必要条件，只要IEI计算过程是无量纲的，就满足此性质，五指标都满足。

不平等指数H的数值分解满足：同一组内部收入如何转移都不影响组间HB，不同组间转移变化复杂，需具体分析；相对而言，Hw越小，则HB越接近于Z指数。

2 我国家庭人均收入不平等的测度

由于我国家庭人均收入（家庭年收入/家庭总人数）、人口规模存在显著差异，因此基于中国家庭金融调查数据（CHFS，2017年），根据家庭规模加权测度我国家庭人均收入不平等程度更合理。为便于度量IEI，删除人均年收入0元以下家庭，经预处理，最终采用39184个家庭作为样本，其中城乡分别有26835、12349 个家庭。家庭人均负收入真实存在，但样本量很少且部分家庭的负收入很高（经营亏损或家庭发生重大变故），而IEI通常只能处理正数，如果将数据平移为正数（通常因最小值太小而平移量很大），则可能改变IEI，且不同评价对象的平移差距很大，难以比较，可能得到不合理的结果，故删除。人们普遍认知的收入是正数，虽然上述数据预处理方式有值得商榷之处，但所得数据反映的整体规律是可信的。

2.1 收入分布规律

令X表示家庭人均年收入（简称人均收入），X0、X1分别表示城镇、农村的家庭人均年收入，单位为千元，其描述性统计见表2，全国家庭人数的分布规律见下页表3。

表2 人均收入描述性统计

表3 全国家庭人数的分布规律

由表2和表3可知：

（1）城镇人均收入的均值（40.307）、中位数（26.018）远大于农村人均收入的均值（14.705）和中位数（8.000），这表明：我国城乡收入差距很大，城镇普通居民家庭人均收入约为4.03万元，而农村普通居民家庭人均收入约为1.47万元，从家庭人均收入角度看，城镇居民家庭人均收入比农村大约高2.56万元，而中位数约高1.80万元。

（2）从家庭人数看，两口之家最多，其次为三口之家、四口之家、五口之家、一口之家等。可见，我国主要呈现小家庭趋势，家庭规模与父辈相比已有较大变化。两口之家将是主流，他们多是没有子女的夫妻或子女已独立成家的中老年家庭，三口之家多是夫妻加一个子女，这也是独生子女政策及低生育率的必然结果。一口之家占比较高，他们多是丧偶老人，比较孤独，因此政府要关注孤寡老人的养老问题，鼓励子女多回家与父母交流、提供力所能及的帮助。随着三孩政策的放开，我国家庭规模会有扩大趋势，这时，度量不平等程度更需要考虑家庭规模。

城镇、农村家庭人均收入的核密度估计①选用高斯核，带宽为1。曲线见图2，显然，城镇家庭人均收入X0（偏度为24.118，峰度为979.780）与农村家庭人均收入X1（偏度为29.657，峰度为1380.487）都是右偏斜分布、尖峰分布，但是他们的分布规律存在明显差异，X0尾部更厚且更加平坦。城镇、农村家庭人均收入分别在2 万元、1 万元处的概率比较大，消费力较弱（消费在本质上依赖收入），而当前高房价、高教育、高医疗又是必需品，故刺激消费的关键是提高普通居民收入。

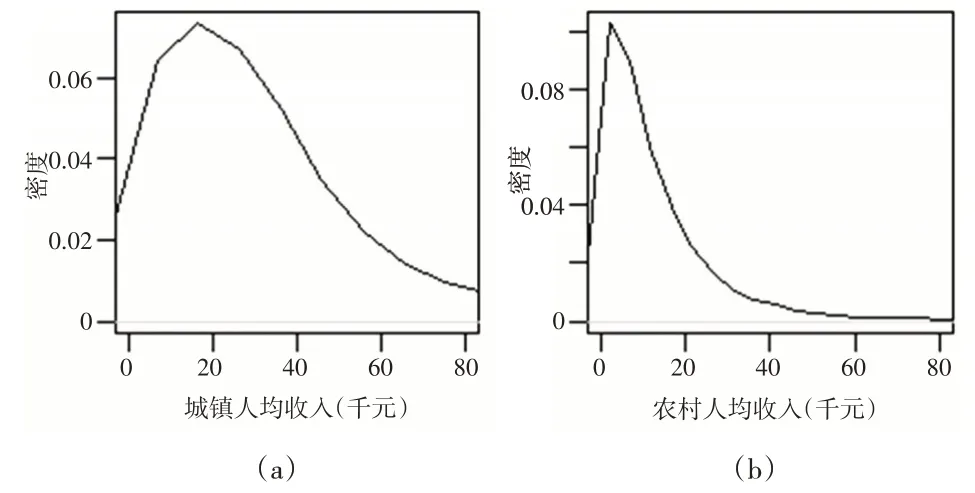
图2 核密度估计曲线

2.2 收入不平等测度与分解

由于每个家庭人数存在差异，因此在度量收入不平等时需要考虑家庭人数，具体操作为：将家庭人均收入y1，…，yr分别重复n1，n2，…，nr次（度量每个家庭人数的重要性）构成数据集{xi，i=1，…，n}，n=n1+…+nr为所有家庭的总人数，再根据{xi，i=1，…，n}直接计算传统CV、T指数、Gini系数、C指数、Z指数，并探讨IEI的数值分解，结果见表4。

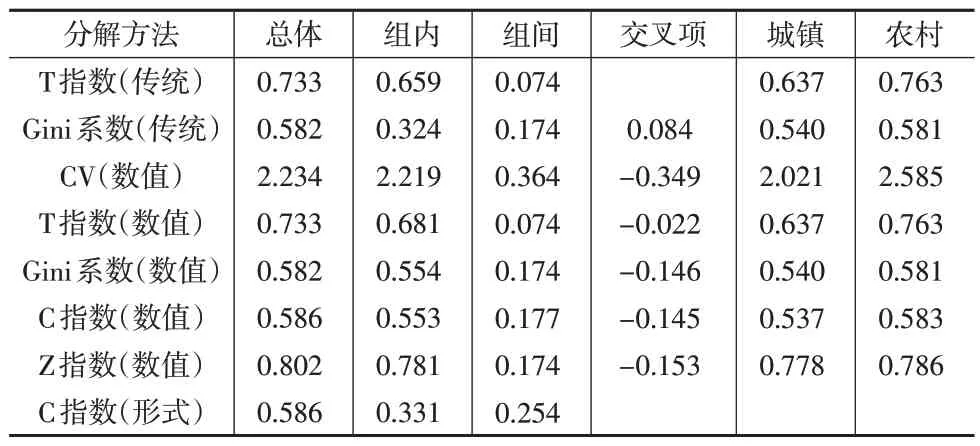
表4 IEI分解结果

（1）从IEI看，农村家庭人均收入不平等程度均大于城镇家庭人均收入不平等程度，这主要因为农村机会较少，阶层更易固化。根据Gini系数可知，我国整体（0.582）、城镇（0.540）和农村（0.581）家庭人均收入Gini系数都超过警戒线0.4，值得重视。

（2）从数值分解看，T 指数传统分解与数值分解的组间取值一致，但对应权重不一样，前者为指标占比，后者为人口占比，Gini 系数分解也有类似规律。Z 指数与Gini 系数的组间差异计算结果基本一致。

（3）C 指数的形式分解与其他分解没有可比性，它实际含义有限，不可过多解读，0.331、0.254分别近似表示城镇、农村观测数据的贡献率。

将我国整体看作虚拟评价对象可看清我国整体状况，也便于各省份认清自己的实际情况。下面对我国整体与29个省份（不含新疆、西藏和港澳台）进行不平等测度，整体上分为两类方法。

方法1：根据前面构成的{xi，i=1，…，n}测算IEI，结果见下页表5。T指数、C指数对应排名略去，这在一定程度上考虑了家庭人数，较合理。

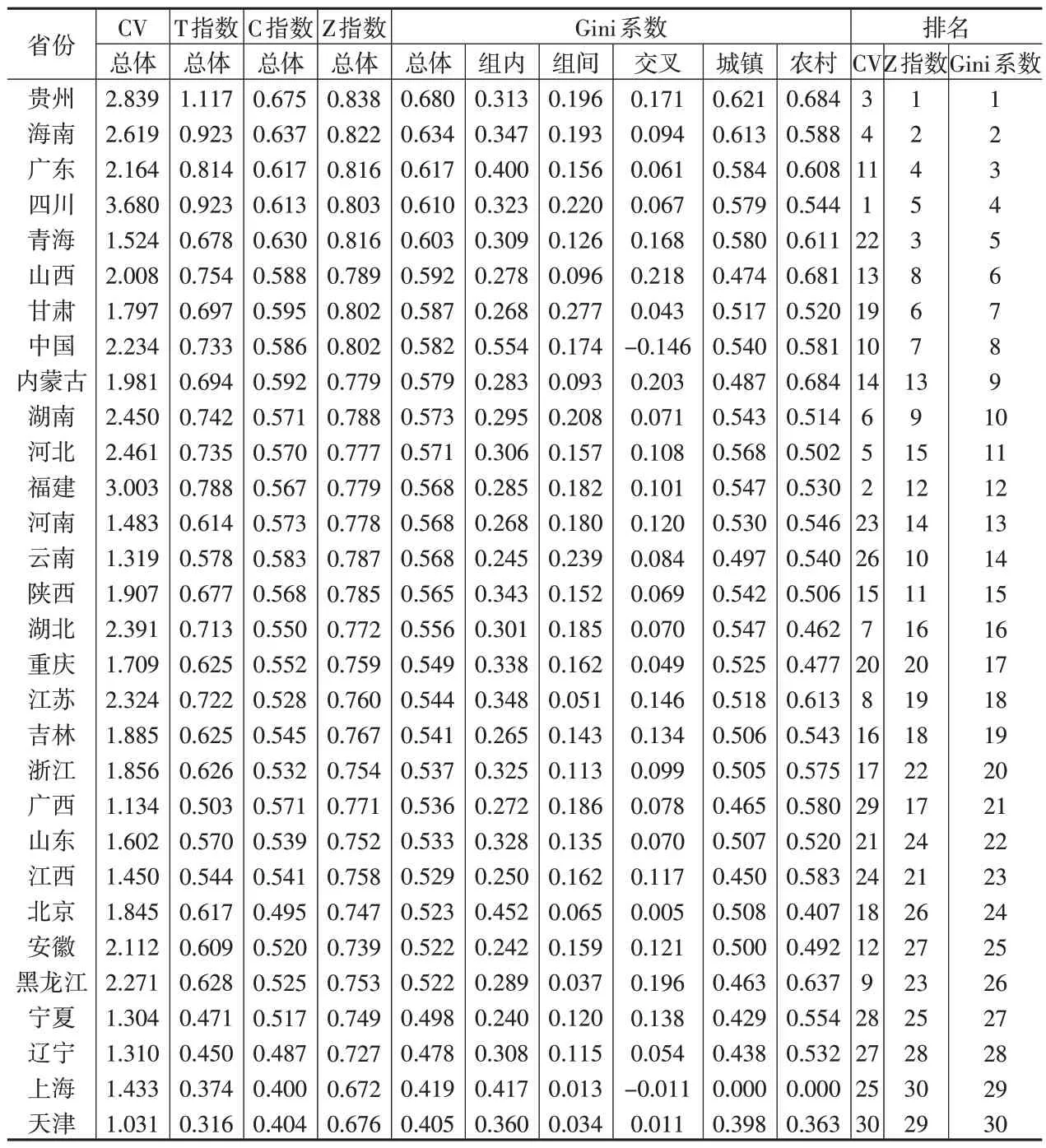
表5 家庭人均收入IEI

方法2：家庭人均收入的加权IEI。将家庭人均收入作为观测值，以家庭人数作为权重分别计算加权CV、加权T指数、加权Gini 系数、加权C 指数、加权Z 指数（家庭人均收入按家庭人数复制后计算Z 指数），按家庭人均收入直接计算Gini系数（不考虑家庭人数），记为Gini0，用来度量我国29 个省份的家庭人均收入的不平等程度，结果见下页表6，T 指数、加权C 指数对应排名略去。方法1、方法2中的Z 指数计算原理一致，虽然具体计算时，因采用的{xi，i=1，…，n}的精确度不同而存在细微差异，但对应排名完全一致。

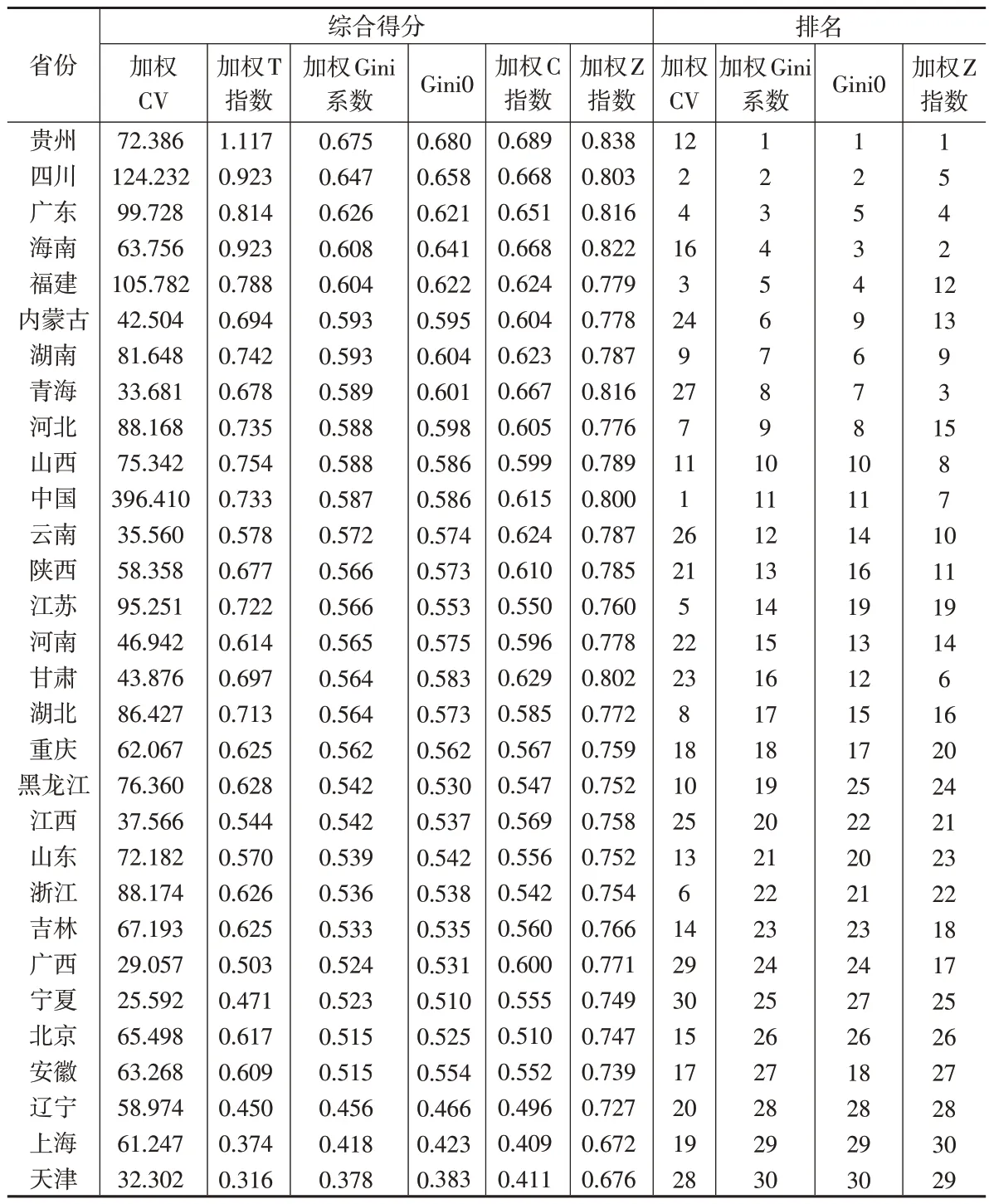
表6 家庭人均收入的加权IEI

根据表5 至后文表7，结论有：

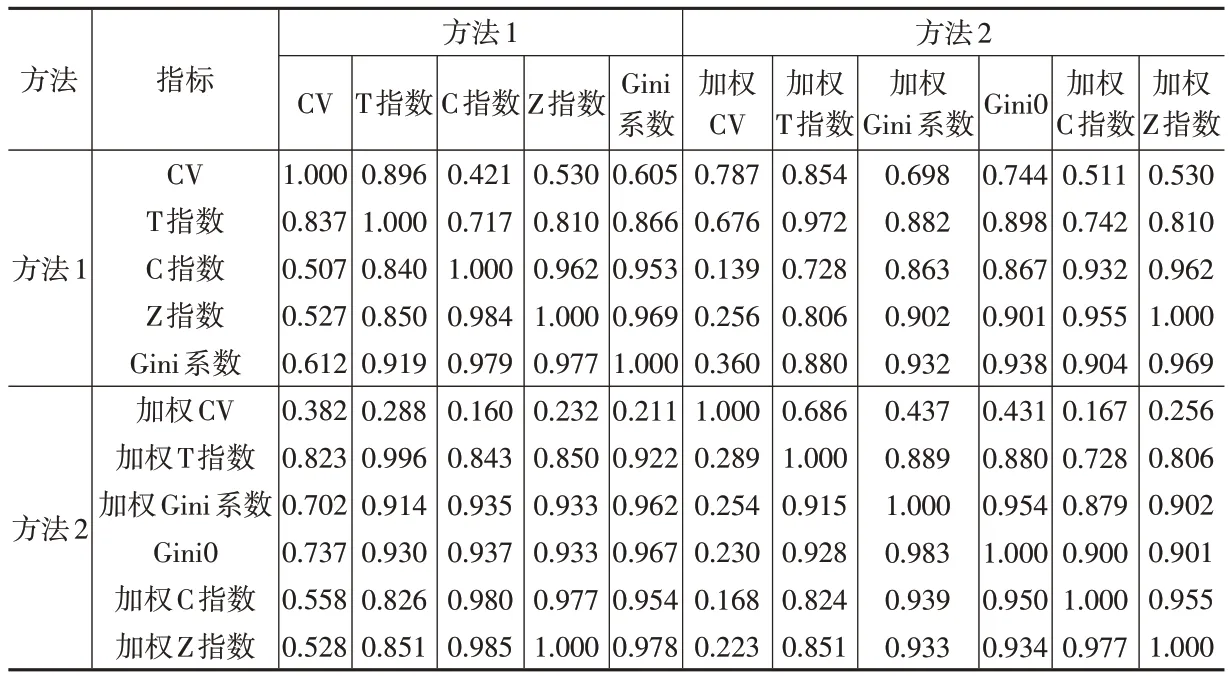
表7 IEI间的相关系数ρ（下三角）与排名间的相关系数ρs（上三角）

（1）两种方法对应CV的ρ和ρs分别为0.382 和0.787，数值较小，且CV 与其他指标对应的ρ都不大。另外，根据加权CV（方法2），北京、上海的收入不平等排名分别为15、19，这与其他IEI的度量结果差距很大，因此根据加权CV 度量不平等程度效果较差。这表明CV只是简单的离散度量，稳定性较差，不适合进行不平等度量。因此，下面分析不再考虑CV 指标，即方法1 有4 个指标，方法2也有4个指标。

（2）从理论上看，考虑家庭人数的IEI更合理。上述所有IEI中只有Gini0没有考虑家庭人数，但由于样本容量较大，Gini0 实际测算效果也较好，它与方法1、方法2 的IEI对应ρ的最小值为0.928（不考虑CV）。这表明，直接根据家庭人均收入测算不平等程度可信度依然很高。

（3）根据表7，方法1、方法2 对应的4 个IEI指标都有效，符合实际，建议优先采用世界通用的Gini系数度量不平等程度。

根据Gini系数所得的经济结论主要有：

（1）从全国家庭人均收入看，农村Gini系数大于城镇Gini 系数，但是从各个省份看，有11个省份（海南、四川、湖南、湖北、河北、福建、陕西、重庆、北京、安徽、天津）的农村Gini系数小于城镇Gini系数。因此，我国整体上农村Gini系数大于城镇Gini系数。

（2）方法2 中加权Gini 系数和Gini0 的ρ=0.983，ρs=0.954，这表明考虑家庭人数的加权Gini系数与忽略家庭人数的Gini0相关性很强，权重只是起到微调作用。江苏、黑龙江根据加权Gini 系数排名分别为14、19，根据Gini0排名分别为19、25，安徽根据加权Gini系数排名为27，根据Gini0排名为18，可见，如果考虑家庭人数，则安徽收入不平等程度下降很多，即收入差距大的家庭人数相对少，而收入差距小的家庭人数相对多。

（3）国家统计局公布的2017 年居民收入Gini 系数为0.47。根据CHFS 提供的数据，2017 年家庭人均收入Gini 系数略高于0.58，大致比居民收入Gini系数高0.11。居民收入Gini系数与家庭人均收入Gini系数是从两个视角度量我国收入的不平等程度，前者以个人为单位，后者以家庭为单位求平均，共同之处是Gini系数已超过警戒线0.4，贫富差距较大。另外，以家庭为单位求人均收入对Gini系数的影响有两个方面：一方面，婚姻组合的基本原则是强强联合、弱弱联合，这会放大Gini 系数；另一方面，以家庭为单位求平均会缩小家庭成员间的差异，减小Gini系数，哪一方面占据主导地位需进一步研究。

（4）由表5中的Gini系数排名可知，家庭人均收入不平等排在前5位的依次为贵州、海南、广东、四川、青海，排在后5位的依次为天津、上海、辽宁、宁夏、黑龙江。北京排在第24 位，即北京家庭人均收入的不平等程度较低。

（5）根据组间Gini 系数度量各省份的城乡差异，不平等程度排在前5位的依次为甘肃、云南、四川、湖南、贵州，排在后5 位的依次为上海、天津、黑龙江、江苏、北京。上海目前已不分城乡（都是城镇居民），故不存在城乡差异。可见，较落后的甘肃、云南、贵州的城乡差距比较大。

3 结论

不同IEI 有不同的适用范围与特点，这就需要从多个角度测量，避免单一指标的片面性。对于家庭人均收入，有两种思路构造基于家庭人数的IEI：第一种方法是先将家庭人均收入按家庭人数复制，再采用传统IEI测算；第二种方法是直接将传统IEI推广到加权场合。本文的主要结论有：

（1）2017年我国家庭人均收入的Gini系数略高于0.58，大致比居民收入Gini 系数高0.11，可见，我国收入差距较大。另外，城镇、农村普通家庭人均收入中位数分别为2.6万元、0.8万元，消费力较低。

（2）整体而言，我国农村家庭人均收入不平等程度高于城镇，发达地区的城乡差距较小，落后地区的城乡差距反而较大。相对而言，北京家庭人均收入的不平等程度处于较低水平，但差距依然较大，天津、上海的家庭人均收入的不平等程度处于最后两位，值得其他省份学习。