系统耦合协同评价模型的改进及其应用

朱 俊

（广西民族师范学院 经济与管理学院，广西 崇左 532200）

0 引言

协同评价一直是社会经济发展过程中对多系统进行关系分析和同步性程度评价的科学方法。比较经典的协同评价模型主要是基于物理学中的耦合概念所提出的耦合协同评价模型，该模型主要是通过计算耦合度、协调指数、耦合协调度来反映多个系统之间的协同水平。然而，经典耦合协调度模型存在一些不足之处，主要表现在：评价结果对数据标准化方法依赖性强、对评价系统的数据特征有一定要求（难以处理负值或零值）等，这些问题限制了其结果的合理性和解释力度。本文旨在对经典耦合协同模型进行改进，以期能够更好地将其应用于解决社会经济发展中的协同评价问题，并丰富和完善研究方法，增强模型的适用性。

现有研究已取得丰硕成果。一是耦合协同模型的提出及广泛应用[1—6]。二是协同评价的其他模型[7,8]。三是对经典耦合协同模型的改进[9—14]。

当前学术界对经典耦合协调度模型的应用及改进已经较为成熟，且多以双系统应用为主，在模型改进方面虽取得了一些成果，如对参数进行优化、对协调范围进行重新划分等，但这些改进并未从根本上解决经典耦合协调度模型的几个不足，如数据标准化、非负性、方向性、区分度、稳健性等问题，而这些问题的存在将使得模型的应用效果大打折扣，甚至得出错误的结论，将决策分析引入误区。鉴于此，本文针对经典耦合协同模型存在的不足之处进行改进，提出合理性与稳健性更强的基于增长率和相离度的协同评价模型（Growth rate&Separation degree Cooperative Evaluation，简称GSCE模型），以期为解决社会经济发展中多系统协同发展的评价问题提供参考。

1 经典耦合协同模型及问题分析

1.1 经典耦合协同模型简介

经典耦合协同模型（Coupling Cooperative Evaluation，简称CCE模型）包含三个计算公式，具体如下：

其中，F(Xi)表示第i个系统的发展水平，将计算所得的C值称为耦合度，T值称为协调指数，D值称为耦合协调度。

该模型旨在通过耦合度来刻画系统之间的离差水平，显然在满足F(Xi)≥0 的条件下，有0 ≤C≤1，且各系统的发展水平F(Xi)的取值越均衡，耦合度C值越接近于1，反之则越接近于0。协调指数通过各系统发展水平的加权平均值来衡量系统整体水平，根据0 ≤F(Xi)≤1 的取值条件，T值满足0 ≤T≤1，且T值随F(Xi)取值的增加而增加，其中αi称为贡献度，αi越大，代表决策者越重视系统Xi的发展，T值越接近于1 代表整个系统的发展水平越高。耦合协调度D在考虑了系统均衡性与系统整体水平的基础上用于衡量系统间的协同水平，其取值范围为0 ≤D≤1，D值越大说明整个系统协同水平越高。

在实际应用中，CCE 模型多用于衡量两个系统（X和Y）之间的协同水平，此时n=2，模型可进一步简化为：

根据耦合协调度的取值范围，将其划分为10 个协调等级，耦合协调度及协调类型的对应关系如表1所示。

表1 耦合协调等级分类

基于表1中的10个协调等级，龚雪和荆林波（2022）[15]进一步将其划分为3 大类，即：当0＜D≤0.4 时，为不可接受区间；当0.4＜D≤0.6 时，为过渡区间；当0.6＜D≤1时，为可接受区间。大多数学者认为X和Y所对应的两个系统同样重要[16,17]，故一般取α=0.5，此时将C和T代入T=，化简可得：

此时，耦合协调度为F(X)与F(Y)的几何平均数的平方根。

1.2 经典耦合协同模型存在的问题分析

CCE模型在应用时存在以下几点不足：

（1）标准化：该方法默认所有变量取值均在[0,1]区间内，因此一般要求采用“max-min”归一化方法，使数据全部处于[0,1]区间内（往往也不能取0，需要通过平移避免出现0 值）。但CCE 模型并未明确指定数据的标准化方法，故采用不同的标准化方法将得到不同的测度结果。

（2）非负性：数据中不允许出现负值，否则将导致计算无法进行。现实中面临着诸多负值的情形，如采用主成分分析计算所得的系统发展水平（综合评价值）往往存在负值，强行将其转化为正值后可能导致语义上无法解释或改变数据间的差异水平。

（3）方向性：从CCE 模型所给出的测度公式中只能看出协调程度，当存在不协调时，无法清晰知晓谁领先或是谁落后。

（4）区分度：CCE 模型所给出的耦合协调度公式区分能力不强，即使数据发展趋势存在较大差异，也容易出现“形势一片大好”的结论，不利于发现并解决实际问题。

（5）稳健性：当增加数据时，CCE模型的测度结果将发生改变，重新计算将导致结果发生较大变化。

针对问题（3），邓宗兵等（2019）[18]为了探究双系统中的相对发展类型，构建了相对发展度指数，即β=F(X)/F(Y)。当0 ＜β≤0.9 时，认为系统X的发展滞后于系统Y；当0.9 ＜β≤1.1 时，系统X与系统Y同步化发展；当β＞1.1时，系统X的发展领先于系统Y。

2 基于增长率和相离度的协同评价模型优化

2.1 改进的协同评价模型

针对双系统在时间序列数据中的协同评价问题，本文构建基于增长率和相离度的协同评价模型（简称GSCE模型）。

（1）在基于时间序列的协同评价中，协同水平的计算应充分考虑不同时期的取值情况，而非仅以当期数据为依据。在模型（2）中，对于递增的时间序列，最后一期数据Dt=n=1 几乎是完全可预测的结果，显然这个“优质协调”且稳定的结果没有充分考虑到实际情况的复杂性。因此，本文基于时间序列数据的发展特性，给出增长率的计算公式：

其中，X*的取值可以分为两种，即X*=Xt-1或X*=X1（以前者为主）。当X*=Xt-1时，g(Xt)为t时期的环比增长率（相对于前一个时期t-1 而言）；当X*=X1时，g(Xt)为t时期的定基增长率（相对于第1个时期t=1而言）。考虑到现实数据的复杂性，公式中兼顾了原始数据为负值的情形，并规定当X*=0 时，g(Xt)=1（实际计算中可选择X*≠0 的时期作为基期）。为表达方便，在公式中省略时期标记t，g(Yt)的含义同理。

（2）为进一步衡量系统X与系统Y发展水平的差异，基于最大化离差的思想构造相离度公式：

其中，k（k＞0）为常数，称为调节系数。加入调节系数k主要是为了避免当g(X)与g(Y)符号相反时，S恒等于1 或-1 而不随g(X)与g(Y)的值变化的情形。由式（5）可知，S随k的增加单调递减，即k越大，S将越小。实验数据表明，k∈(0，1]时较为理想，k值太大将掩盖原始数据的增长特性，使计算结果过于平稳，区分度降低。

显然，相离度的计算公式可兼容增长率为负值或0值的情形，且相离度的取值范围为S∈(-1，1)。特别地，当g(X)=g(Y)时，S=0，表明系统X与系统Y在该时点不存在差异；当g(X)=-g(Y)＞0 时，，g(X)越大，S越接近于1；同理，当g(X)=-g(Y)＜0 时，S=-，g(Y)越大，S越接近于-1。

（3）基于相离度，可进一步将其转换为协调度，转换公式如下：

其中，sign(S)为符号运算函数，运算法则为：当S≥0时，sign(S)=1；当S＜0 时，sign(S)=-1。根据相离度S的取值范围，易知C＇∈(-1，0)∪(0，1]，显然C＇值随S值的增加而递减。值得注意的是，C＇的绝对值大小反映系统的协调程度，C＇的符号反映不协调的原因或方向。具体来说，当C＇＜0 时，表明系统Y的发展领先于系统X；当C＇＞0 时，表明系统X的发展领先于系统Y（不存在C＇为0值的情形）。

综上所述，本文构建的双系统时间序列协同评价模型（GSCE模型）完整表述如下：

2.2 GSCE模型性质讨论

为进一步讨论相离度S与g(X)、g(Y)的关系，构造一个二元函数，令：

对比z(x，y)的表达式与模型（7）中的C＇，可知z(x，y)=|C＇|，即z(x，y)反映的是协调度的绝对水平，协调度的符号表示的是系统X与系统Y的相对领先地位。

由表2可以看出，当x≥y时，z随x的增加而递减，随y的增加而递增；反之，当x＜y时，z随x的增加而递增，随y的增加而递减。从另一个角度看，z随|Δ|=|x-y|的增加而递减，随|Δ|=|x-y|的减少而递增。

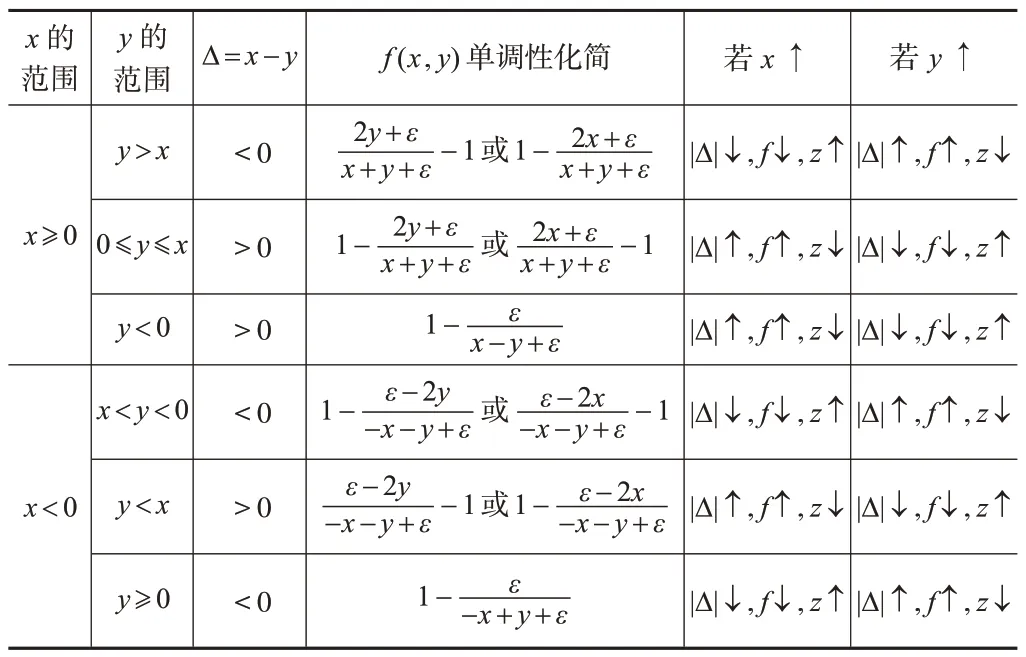
表2 函数单调性讨论

GSCE 模型可以有效解决CCE 模型在应用中所存在的几个问题，具体如下：

（1）数据的标准化问题。CCE模型要求采用0-1归一化方法，使数据全部处于[0,1]区间内，故不同的标准化方法，可能得到不同的测评结果。

显然，GSCE 模型的测评公式采用的增长率是一种相对指标，与指标的单位和量纲无关。因此，GSCE模型无须先对数据进行标准化处理，对于时间序列数据，正常情况下计算的增长率一般都处于[-100%,100%]区间内，即使在极端情况下，一般也不会超出[-300%,300%]区间，这与统计中的3δ准则基本一致。当其中一方超出这个范围时，必然意味着极大程度的不协调。

（2）CCE 模型数据中不允许出现负值，否则将导致计算无法进行。现实问题中面临着诸多负值的情形，强行将其转化为正值后可能导致语义上无法解释。

从GSCE模型的测度公式可以看出，无论是原始数据存在负值，还是增长率存在负值，都可以较好地处理。当原始数据为负值或正值且不断增加时，所对应的增长率均为正值，不影响计算；当原始数据为负值或正值且不断减少时，所对应的增长率均为负值，此时协调度公式仍然适用。

（3）CCE 模型所给出的测度公式只能计算协调程度，当存在不协调时，无法清晰知晓谁领先谁落后的相对大小关系。

GSCE 模型的结果则可以体现X与Y之间的相对大小关系，显然，当g(X)≥g(Y)时，S≥0，C＇∈(0，1]，表示系统X的发展领先于系统Y，C＇越接近于0+，则领先程度越大；当g(X)＜g(Y)时，S＜0，C＇∈(-1，0)，表示系统X的发展落后于系统Y，C＇ 越接近于0-，则落后程度越大。根据公式不仅可以计算协调程度的大小，还可以判断不协调的方向。

（4）CCE 模型所给出的协调度公式区分能力不强，即使数据发展趋势存在较大差异，也容易得出“形势一片大好”的结论，不利于发现并解决问题。例如，若X与Y两个时间序列均逐渐增加，则标准化之后均有最后一项F(Xn)=F(Yn)=1，则必有D=1，得到“优质协调”的结论，这将造成“求解前的结果可预知性与确定性”与实际决策问题可能不符。更一般地讲，若X与Y两个时间序列整体上均呈递增趋势，则原公式的判定结果基本是从“极度失调”向“优质协调”转变，呈现“形势一片大好”的局面，但事实往往并非如此。

反观GSCE模型的测度公式，由于采用了增长率的方式进行计算，考虑了对象在不同时期的发展趋势，且协调度更看重g(X)与g(Y)的相对比较，因此可能在一开始就出现高度协调的局面，甚至是从协调向失调转变，更能反映出实际应用中所面临的问题。

（5）测度结果的稳健性问题。当增加数据时，CCE 模型的测度结果将不再保持，重新计算将导致结果发生变化。从CCE 模型的公式不难看出，若在已有基础上增加数据（以递增序列为例），则原数据中的最大值将在新一轮的标准化下变成中间水平的值，此时所得的耦合协调度也会降低，即当增加几期新数据时，将改变原有的协调程度结论，这显然是不合适的。

由GSCE模型的测度公式可知，协调度仅依赖于当期数据和前一期数据，而与头部和尾部数据无关，所以当向前或向后延伸增加数据时，不会改变已有的协调度测度结果，协调度更具稳健性。

3 GSCE模型数值分析与参数验证

为进一步说明GSCE 模型对变量g(X)、g(Y)和参数k的单调性与敏感度问题，本文通过实验分析的方式进行验证。

（1）协调度对不同g(X)的敏感度

分别取g(X)=-1、-0.5、0、0.5、1，g(Y) 的取值范围是[-3,3]，步长为0.1，根据模型（7）中的公式分别拟合出协调度C＇ 随g(X)与g(Y)的变化趋势，如图1 所示（固定g(Y)取某个特定值时，讨论C＇随g(X)的变化规律同理，不再赘述）。

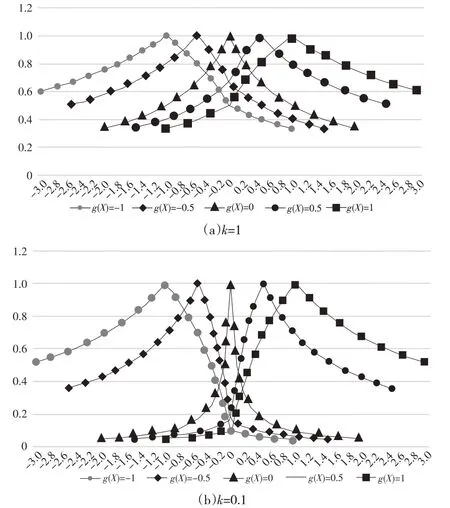
图1 协调度在不同g（X）下随g（Y）的变化规律

由图1可知：①图形整体上以g(Y)=g(X)值所处位置为中心位置，呈现“中间高、两头低”的变化趋势，表明g(Y)与g(X)的差值越大，则协调度越低；②g(X)越大，协调度曲线整体越往右移动；③当g(Y)与g(X)符号相反时，其协调度变化更快，表明虽然差值相同，但由于增长方向相反，“背道而驰”时协调度更低；④当g(X)为0 时，协调度曲线是对称的，其余情况下则不满足对称性；⑤k值越小，协调度波动范围越大，区分能力越强。

（2）协调度对不同k值的敏感度

k分别取值为0.01、0.1、0.5、1、2 进行测试，将g(Y)的值在[g(X)-1,g(X)+1]的范围内依次取值，步长为0.05，根据模型（7）拟合出协调度C＇随g(X)与g(Y)的变化趋势，如图2 所示（固定g(Y)取某个特定值时，讨论C＇ 随g(X)的变化规律同理，不再赘述）。

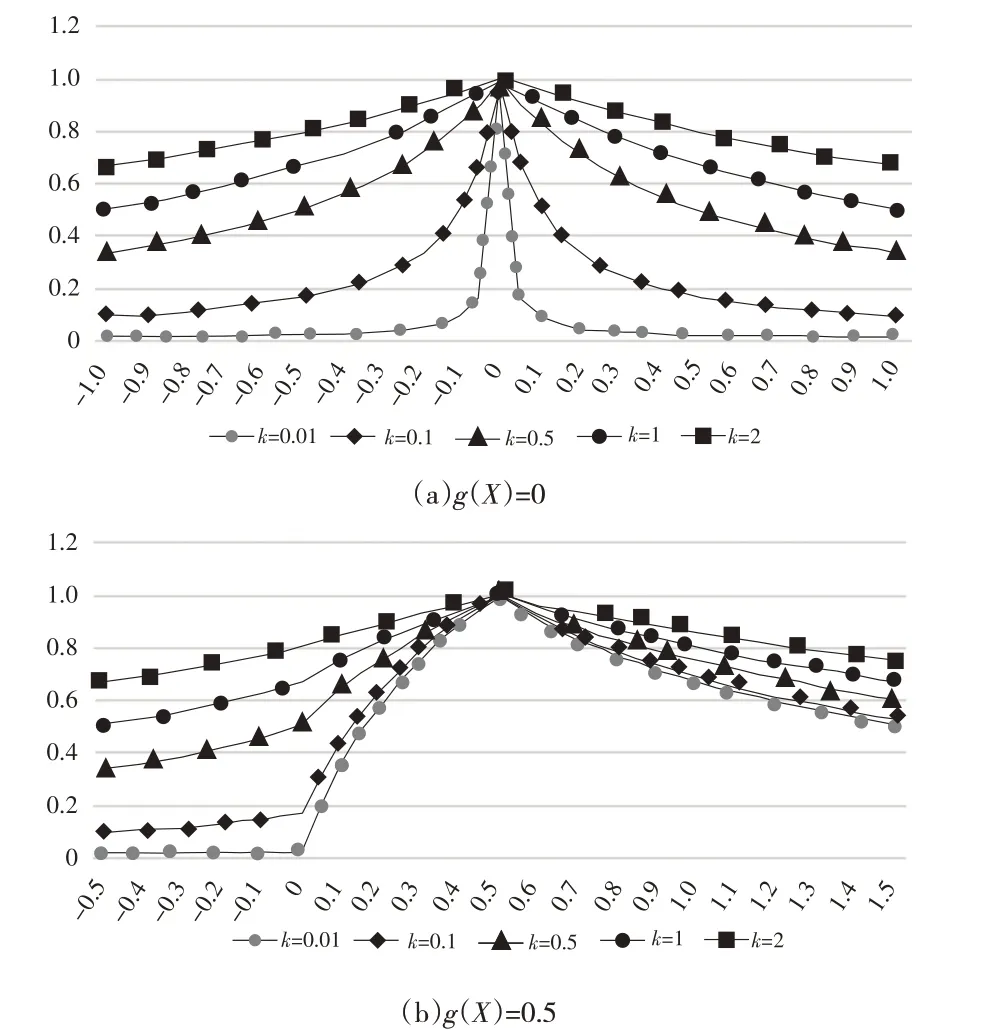
图2 协调度在不同k值下随g（Y）的变化规律

由图2可知：①k值越小，协调度变化越快，波动性越大；②当k=0.01 时，即使是10%的波动[-0.1,0.1]，也将使协调度从1 断崖式下降至0.167，显然其对数据的误差容忍度太过敏感；③当k=2 时，即便是100%的波动[-1,1]，协调度仍然高达0.667，显然其对数据的误差容忍过于宽松。

数据显示，当g(X)=0 时，k=0.5 所对应的协调度变化趋势较为符合数据之间差异所反映的协同事实：当差异为5%时，协调度为0.91；当差异为10%时，协调度为0.83；当差异为20%时，协同度为0.71；当差异为30%时，协调度为0.63；当差异达到50%以上时，协调度下降为0.50，但针对较大差异的数据波动，协调度的变化仍显得比较宽松。当g(X)=0 时，k=0.1所对应的协调度变化趋势具有更强的区分能力，但在峰值附近5%的波动也将导致协调度从1降低至0.667。

鉴于此，本文对k值的确定不做严格限定，但从现实数据及大量测试经验来看，由于g(X)（或g(Y)）有更大概率处于[0,0.5（]甚至是[0.05,0.3]）的范围，因此k值的选择一般可在0.1～0.5 浮动，具体可由决策者结合实际情况选取。

4 GSCE模型用于系统评价的算例验证

为进一步验证GSCE 模型测度公式对CCE 模型的改进效果，本文选取国内生产总值（单位：亿元，记为序列X）和对外贸易进出口总额（单位：亿元，记为序列Y）这两个有代表性的指标进行计算，以评估我国近年来经济发展总体水平和对外贸易总体水平之间的协同情况，时间跨度为2002—2021 年，数据来源于国家统计局官方网站（http://www.stats.gov.cn/），原始数据如下页表3所示。

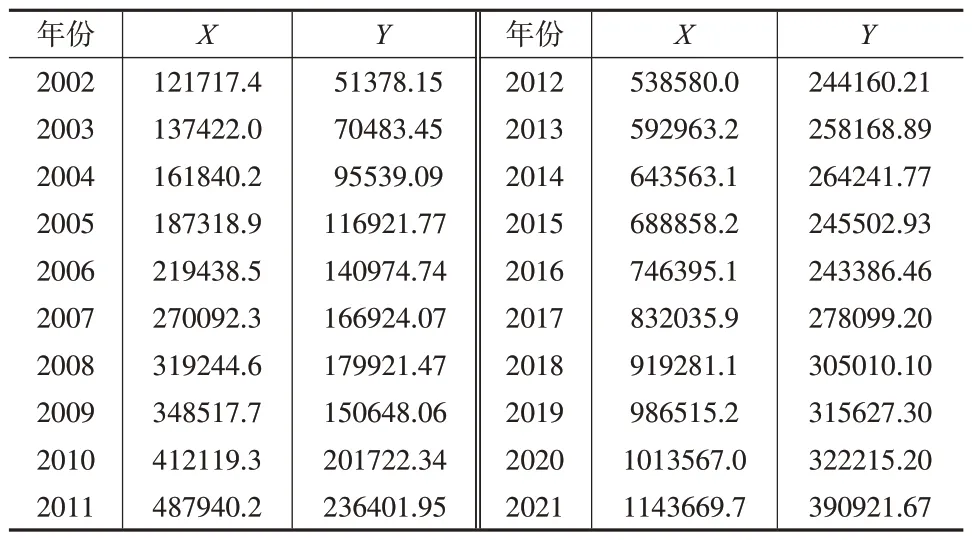
表3 国内生产总值与对外贸易进出口总额原始数据

先使用2002—2011 年的数据，采用CCE 模型进行计算，再加入2012—2021年的数据进行对比。由于GSCE模型不受数据量的影响，因此无须分阶段进行。CCE模型和GSCE 模型所得结果分别如表4 至表6（CCE 模型）和表7（GSCE模型）所示。

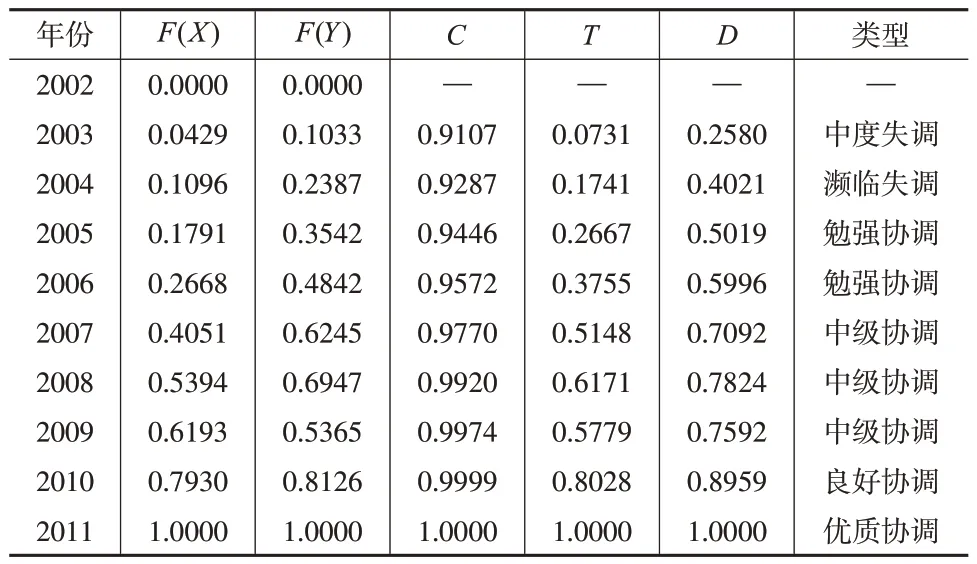
表4 CCE模型计算结果（2002—2011年）

为了更好地对比增加数据前后CCE 模型的协调程度差异，将表4 和表5 中时期相同的部分（2002—2011年）的数据结果整理后进行对比，其中，等级差为表4 中的协调类型与表5中的协调类型的等级之差，结果如表6所示。

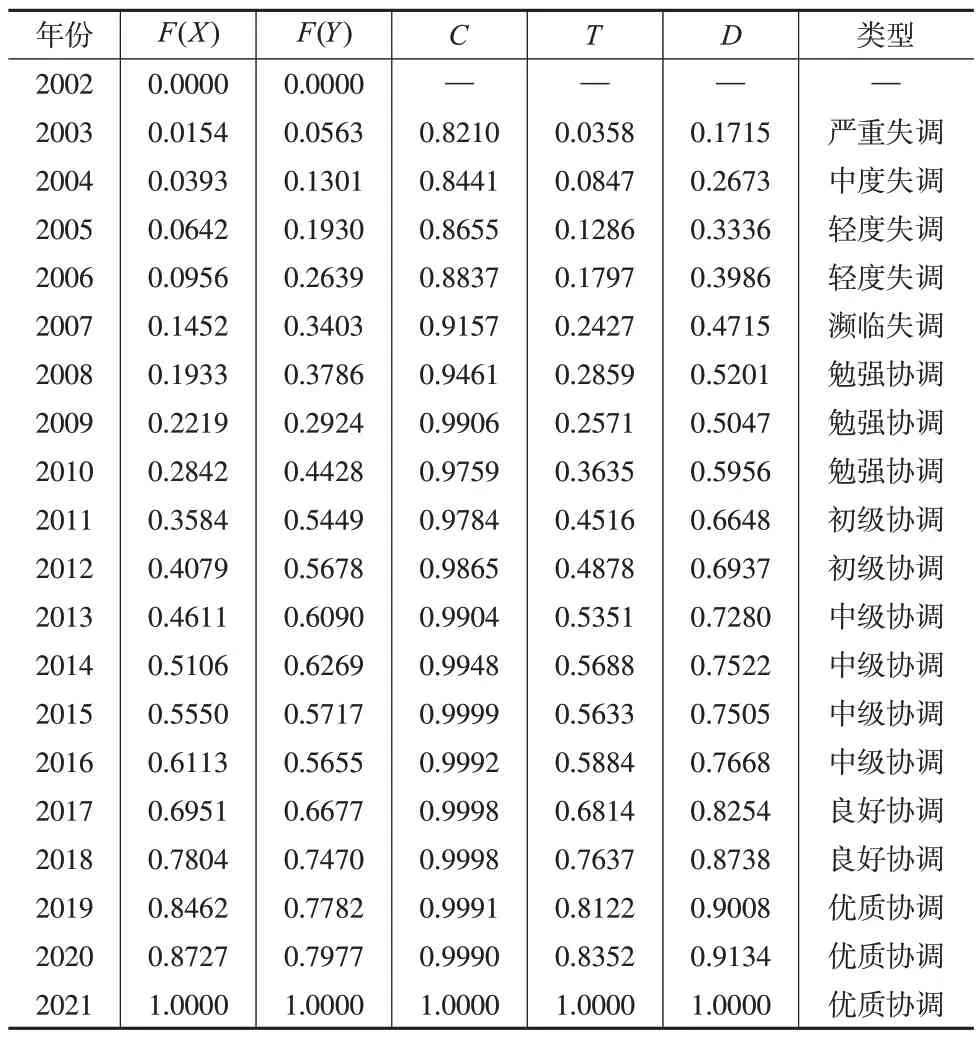
表5 CCE模型计算结果（2002—2021年）

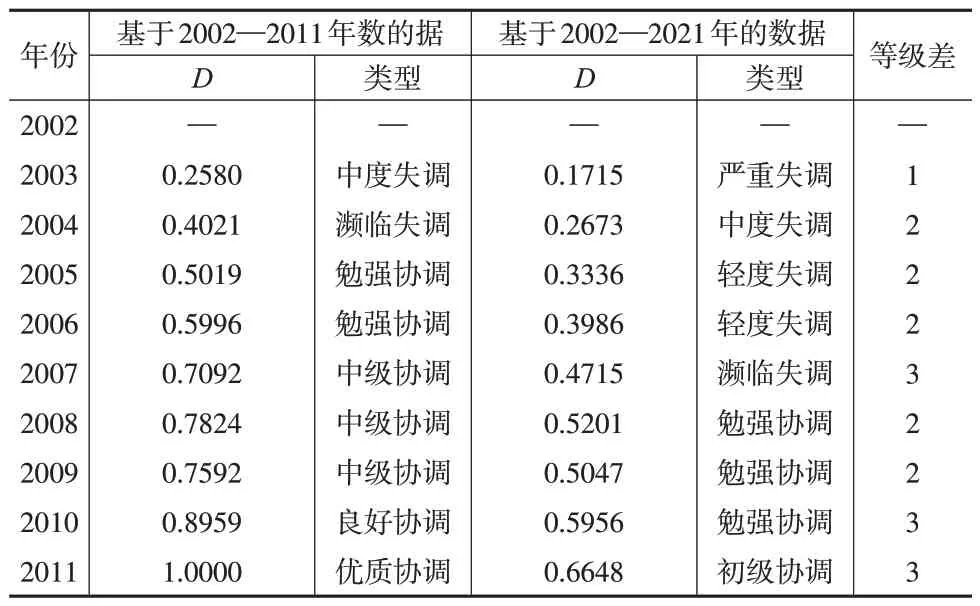
表6 CCE模型数据增加前后协调等级差异对比

由表4结果可知，当模型数据截止到2011年时，D值从2003 年的0.2580 快速增加至2011 年的1.0000，此时2011年的协调结论为“优质协调”。由表5可知，当数据延伸至2021年时，D值从2003年的0.1715逐步增加至2021年的1.0000，增速明显放缓，此时2011年的D值为0.6648，协调结论为“初级协调”。由表6中的对比数据可知，针对2002—2011 年的几乎所有年份，D值出现了明显的前后不一致，等级差最小为1，最大为3，且随着时间的推移，等级差呈递增趋势。以2011 年为例，其耦合协调度取决于当时尚未发生的事件（2012—2021 年），若进一步增加数据，可以预知其协调程度和等级将进一步降低，对事物的评价应基于当前状况并结合历史数据给出，而不是基于未来，因此这样的评价结果显然是不合理的。

表7结果显示，协调度并非随着时间的推移呈逐年增加的趋势，而是波动、交替出现，不再遵循“事前可以预判，形势一片大好”的规律。其中“优质协调”共有6 个年份，分别为2006 年、2007 年、2011 年、2017 年、2018 年、2020年，既非连续年份，也不全是近期年份，而是交替穿插于整个时段。再者，2015年出现了“濒临失调”的局面，究其原因，是由于相较于2014 年，2015 年国内生产总值稳步增长，但对外贸易进出口总额却出现了罕见的大幅度下跌，因此相比于CCE 模型的“良好协调”结论，本文认为将其判定为“濒临失调”更符合实际。从官方披露的数据来看，导致2015年对外贸易进出口总额大幅下降的原因主要在于国际市场需求的变化使得加工贸易进出口下降近10%，其中传统劳动密集型产品出口下降更多，如对俄罗斯出口下降35.2%，对巴西出口下降21.4%。

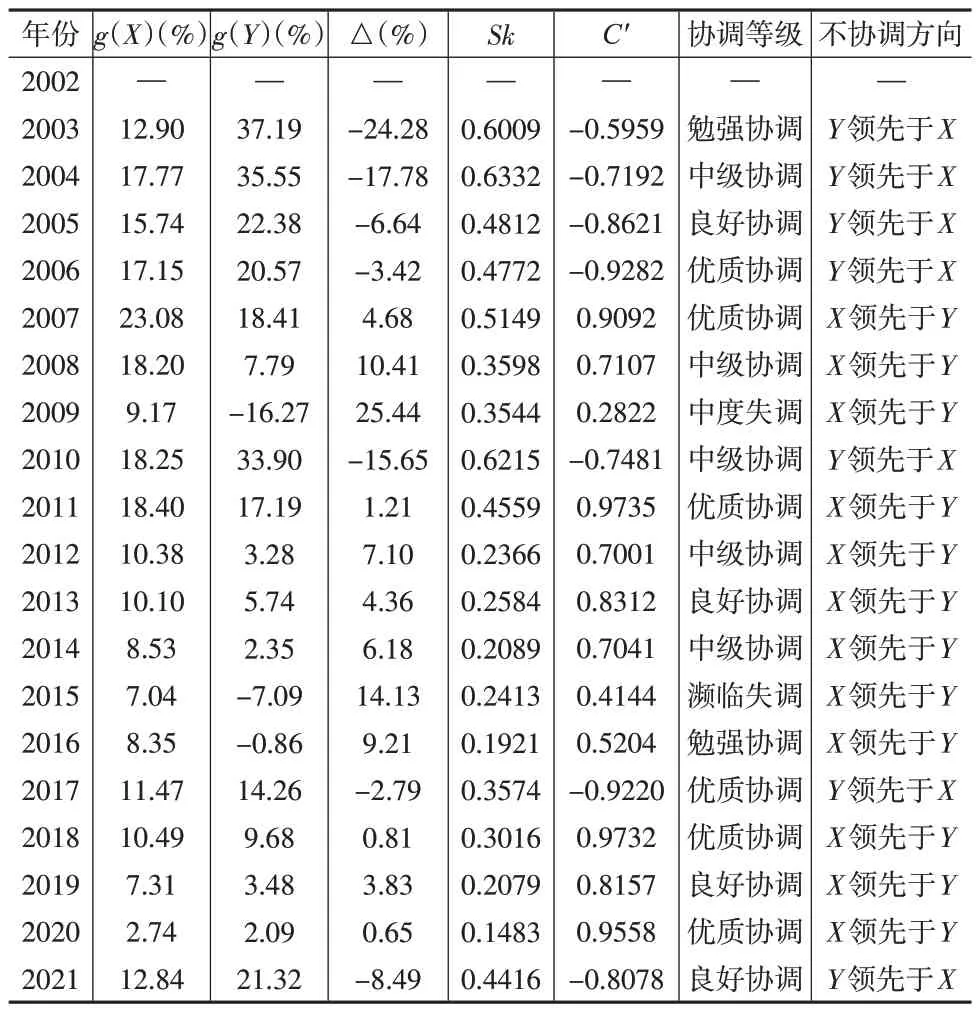
表7 GSCE模型计算结果

5 GSCE模型的进一步扩展

本文所提出的GSCE 模型主要用于计算双系统的时序数据，针对多系统或非时序数据，可在此基础上根据需要进一步优化，主要思路如下：

（1）若是针对多系统时间序列的协同评价问题，在应用GSCE 模型时，可先分别计算双系统间的两两协调度，如此可分别评估系统间的协调度及不协调的方向，再针对各系统分别求平均协调度和总体协调度。此时的模型扩展步骤如下：

步骤1：令X=(X1，X2，…，Xn)表示n个待评价系统，根据模型（7）求得系统间t时刻的两两协调度为C＇t=(C＇ij)n×n，其中，C＇ij表示系统Xi相对于系统Xj的协调度（为表述简便，在符号表达上省略时间下标t），即：

其中，C＇ij=-C＇ji(i≠j)，C＇ii=1，表明系统Xi与其自身是完全协调的，系统Xi与系统Xj的协调度具有互反性（数值相等，符号相反）。

步骤2：计算系统Xi相对于其他所有系统的平均协调度绝对值，。显然AC＇i越大，表明Xi与其他系统的协同水平越高，可进一步推断出，系统Xi的取值越处于中间水平，AC＇i将越大。

步骤3：通过SC＇i的符号判断系统Xi相对于其他所有系统的总体协调度方向，。若SC＇i＞0，表明系统Xi相对于整体而言处于中上水平；反之，则说明Xi处于中下水平，SC＇i的符号仅仅具有方向指示作用。

步骤4：计算系统Xi相对于其他所有系统的综合协调度CC＇i=sign(SC＇i)·AC＇i。若CC＇i＞0，表明系统Xi整体处于领先水平；反之，则表明系统Xi整体处于落后水平。|CC＇i|越大，表明其领先或落后于系统整体的程度越大。

综上所述，多系统时间序列的协同评价模型如下所示：

（2）若是针对双系统非时间序列数据的协同评价问题（如同一时间节点的多个对象），可先整体上按照系统间数据的大小关系升序排列，再将高水平对象的值视为在低水平对象值的基础上的递增数据，此时本文的GSCE模型仍适用于计算双系统非时间序列数据的协调度。

（3）若是针对多系统非时间序列的协同评价问题，可将（1）、（2）中的思想进行融合，即首先按（2）中的方案进行排序，然后按（1）中的方式分别进行两两计算，最后再计算平均协调度和总体协调度。

6 结束语

本文针对经典耦合协同模型在实际应用中的一些问题，深入剖析了导致模型应用出现问题的根源，并针对性地做了改进，提出了一种基于增长率和离差的协同评价模型（GSCE模型）。该模型可以较好地解决经典模型中存在的问题，实例分析也验证了本文所提模型的科学性与合理性。本文所改进的模型仍存在一些不足之处，如在模型扩展中所提到的相关不足，以及对更具解释性和稳健性的评价模型和方法的探讨，这些都将是下一步研究和改进的方向。