基于有向加权图的相似性度量及聚簇划分

刘合富，刘 蓉，赵 强

（1.华中师范大学a.信息化办公室；b.物理科学与技术学院，武汉 430079；2.武汉理工大学 经济学院，武汉 430070）

0 引言

聚簇划分被广泛应用于人与人、人与事物之间的社会关系的划分上。研究社区的聚簇划分对于社区拓扑结构、变动规律、事件预测等具有重要的理论意义和现实价值。聚簇划分的首要任务是社区网络关系的发现。现实社区活动通过用户与事件的互动，往往会产生一些社区网络关系，例如商场商品销售、银企信贷关系、社交网络活动等，都可以通过用户活动构成事件之间的强弱关系[1—3]。将事件关联点当作网络空间节点，将用户的转移需求作为边，将需求的有向关系作为边的方向，将需求强弱程度看作网络的边权，于是上述活动事件节点之间能构成一种基于有向加权网络的社交关系。将加权网络关系图引入事件需求分析，既能清晰地展示事件之间是否存在关联，又能直接明了地表示关联程度的强弱，对个性化推荐、社群划分、社区发现等应用性研究具有重要意义[4]。许多学者进行了社区聚簇划分和聚类分析研究，付立东等（2019）[5]将无向网络图转换为星形邻域网络，建立相似度模型，节点相似度值以共邻节点数占邻居节点总数的比重来计算，用于复杂网络社区划分；邱德红等（2012）[6]提出了一种基于边权值和方向的有向图相似度算法用于聚类发掘；马铁民等（2019）[7]提出了基于用户相似度的Si-user Walker 算法,以无向图节点发生事件次数和类别数为指标构造相似度模型，用于解决网络社交事件推荐问题；任淑霞等（2019）[8]采用马尔科夫链多步转移概率矩阵作为相似度矩阵，完成节点相似图的重构，采用谱聚类实现社区划分。以上相似度计算方法虽然用在社区划分中取得了一定成果，但仍存在一些不足：（1）网络图中节点间直连信息被忽略，仅考虑到邻域节点连接关系；（2）图中节点与邻居节点在边方向、边权等方面的双向连接关系未充分体现；（3）无法呈现节点间事件发生的主被动、信息传递的正逆向、双向边权的对称强度等特征信息变化的问题。以此构建成的网络图，其节点相似性度量不够全面，导致聚簇划分精度不够高。

为提高有向网络图节点相似度计算的准确度，本文基于网络社区用户活动特征，充分考虑节点间连接强度、共邻节点相似性、边方向作用、边权值对称性等对相似度的影响，提出双向度量相似度BDMS（Bi-Directional Measurement Similarity）算法。算法首先建立符合社区活动事务特征的马尔科夫链矩阵；然后，构建有向加权图，其中节点间的相似度主要包含共邻相似度和直连相似度两个部分，并将影响相似度度量的节点直连强度、相邻节点数、边方向、边权值等要素纳入计算，形成相似度邻接矩阵；最后，结合谱聚类无向图切图方式寻找矩阵的相关特征向量进行聚簇划分。为了验证BDMS算法的合理性和有效性，以更清晰地获得聚类分析效果，本文基于真实的高校学生生活和学习数据对其进行验证。

1 有向加权图构建

社区网络空间节点的事件发生关系通常采用图的结构表示，图是在分析具有连接关系的科学和工程问题时常用的一种数据结构[9]。将空间位置或事件看作图的节点，节点之间的关系表示成图的边，包含节点间动态转移事件数量的权重、方向等相互关联的特征信息，形成一张有向加权图。图中节点关系的生成，重点在于图边的定义、权值计算以及边方向的确定。考虑到事件发生过程中节点关系的复杂性，多数相似度算法采用无向加权图来表示节点间的事件连接关系，但是无向加权图忽略了很多节点间主被动关系、互转强度对称性、信息流动方向性等特征信息，难以较为全面地呈现节点之间相似关系的实质。例如：将高校学生网上选修公选课事件视为一项社区网络活动，公选课之间的选课人流量转移关系是双向的，随着教学管理和培养计划的变化，学校提供不同课程的优化策略，课程之间因热度或需求不同可能出现学生选课次数互转现象，该现象若以有向加权图表示能更清晰地勾画出强弱不同的双向转移关系。因此，用有向加权图表示节点事件所发生的关系和特征，具有更好的代表性和呈现性。

本文基于具有马尔科夫特征的社区活动事件的转移关系，采用有向加权图的方式表示。将空间位置节点间发生的事件数量转移看作是一个马尔科夫过程，具有n个节点的状态空间M={1，2，…，n}，以P来表示空间M中节点的事件状态转移概率矩阵，如式（1）所示。

将公式（1）抽象为一个由空间节点、有向边及边权组成的有向加权图，记为:

其中，V={v1，v2，…，vn}是马尔科夫链节点的集合；是代表现实世界中两个实体间的转移关系的双向边的集合；W={W11，W12，…，Wnn}是→中边权的集合，当i≠j时，Wij为马尔科夫链转移概率Pij；(vi，vj)表示由节点vi指向节点vj的边；W对应于有向边(vi，vj)的权Wij记为转移概率Pij，若Wij=0，则表示节点vi到vj无连接边。

式（2）实现了从马尔科夫链的转移概率矩阵向有向加权图的转换，具有方向性和关联关系强度的转移概率的值越大，表示节点间的关系越重要或联系越频繁[10]。式（2）中以节点间的转移概率来表示的图中的边连接权重具有方向性且可能具有不对称性，所涉及的节点关系、边方向、边权重等属性具备明显的事件变化特征。将转移概率矩阵P转化为有向加权图，主要是为了满足社区网络节点在聚类分析中的聚簇划分需要，能更好地了解社区结构、功能以及预测节点分布的行为特征。因此，以马尔科夫链形成的事件转移过程可以抽象为一张有向加权图。

2 有向加权图的节点相似度

2.1 相似度算法分析

计算图节点相似度是进行聚类分析的基础，在社区划分、协同过滤、信息检索、人际关系网络分析等领域有广泛的应用[11]。传统的相似度算法采用局部网络连接信息方法，通过比较邻域节点的向量角度关系、距离大小或图拓扑结构特点来确定节点间的相似性，以反映两个节点的相似程度。常见的算法有余弦相似度[12]、Jaccard 相似度[13]、SimRank 相似度[14]等。其中，余弦相似度衡量节点间的相似性是通过相邻节点向量的夹角余弦值来确定，结果与向量的权重大小无关，仅与向量的方向相关；Jaccard相似度认为节点间的共同邻居数越多，在与两个节点相连的全部节点总数中占比越高，相似度就越高；SimRank 相似度认为如果有共邻节点与两个节点相连，共邻节点之间相似度越高，两个节点相似度也越高。以上算法仅考虑了共邻节点的相关信息，但在节点间存在双向转移事件关系时，至少存在以下不足：（1）未考虑到共邻节点做贡献时具有双向性，并且方向不同、大小不同，贡献可能存在差异。（2）当两个节点直接相连时，产生的亲密性作用被忽略，假如不存在共邻节点，则其相似度为0，与现实不符。（3）采用聚类分析进行聚簇划分的准确率不高。从两个节点之间的相似关联程度来看，共邻节点对节点间相似关系确实存在双向强弱不同的影响，但是两个节点之间的直接互动强度也在一定程度上反映了两者的相似关联性。因此，计算节点相似度时仅考虑共邻节点的贡献是不够全面的。

2.2 有向加权图的BDMS算法

为了更好地评价空间节点的相似性，本文采用BDMS算法来计算相似度，算法的基本流程如下：

步骤1：输入由初始数据集形成的马尔科夫链状态转移概率矩阵P（见式（1））。

步骤2：参照式（2），构建有向加权图G'=(V，→，W)。

步骤3：根据有向加权图G'的节点间矢量信息完成节点间的相似度分解。

步骤4：根据节点边权值、边方向、出度和入度相似度的对称性等信息，计算节点的相似度。

步骤5：输出相似度邻接矩阵。为下一步利用该矩阵进行聚类分析实现聚簇划分做准备。

2.2.1 节点之间的相似度分解

马尔科夫链的一个节点向其他节点转出数量时，也可能接收其他节点转入的数量，整个过程可以建立节点间的双向局部连接关系，依照式（2）形成一个有向加权图，然后通过节点间的双向矢量关联信息来计算相似度。如果将节点v3看作是v1、v2的共邻节点，根据关联矢量方向可以分解为：v3对v1和v2的转移强度存在正反两个方向，如图1中（a）、（b）所示；v1和v2之间的互转强度存在正反两个方向，如图1中（c）所示。

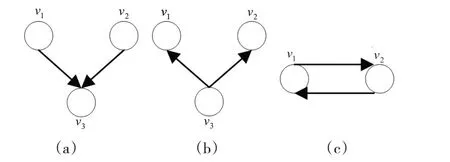
图1 节点间关联矢量分解示意图

于是可以理解有向加权图的两个空间事件节点的相似度由以下三个部分组成：Sin——入度相似度；Sout——出度相似度；LT——两个节点直接相连的亲密度，即直连相似度。其中，入度相似度、出度相似度分别参照余弦相似度的计算方法,从单一方向上与传统方法保持一致，计算公式分别如式（3）、式（4）所示。

其中，N+(i)、N-(i)、N+(j)、N-(j)分别表示节点i和j的入度和出度的邻居节点集合，N+(i)∩N+(j)和N-(i)∩N-(j)分别表节点i和j的入度和出度的共邻节点集合，Pki和Pkj表示共邻节点k对节点i和j的入度转移强度，Pik和Pjk表示节点i和j对共邻节点k的出度转移强度。

2.2.2 算法过程描述和实现

为了降低算法复杂度，在有向加权图的相似性度量定义中，主要综合考虑影响节点相似性的各个因素的作用。算法过程如下：定义两个节点的相似度S(i，j)由共邻相似度ST(i，j)和直连相似度LT(i，j)组成。其中，ST(i，j)由共邻节点对两个节点在双向连接边权值上的贡献决定，并由入度相似度Sin(i，j)和出度相似度Sout(i，j)计算得出，算法计算时，针对不同方向，若两个节点与共邻节点之间有一个方向不直接相连，则该方向的相似度为0；否则，取其共邻节点的边权值纳入计算；直连相似度LT(i，j)由两个节点之间在双向连接边权值上的贡献决定，算法计算时，若两个节点之间有一个方向连接断开，则两者的直连相似度为0，否则取其双向边的权值纳入计算。算法主要步骤如下：

步骤1：计算两个节点的共邻相似度ST(i，j)，如式(5)所示。

其中，Sin(i，j)、Sout(i，j)分别由式（3）、式（4）计算所得。式（5）的算法有两个主要优点：（1）Sin(i，j)和Sout(i，j)的值越大，ST(i，j)越大；（2）Sin(i，j)和Sout(i，j)的值越接近对称，ST(i，j)递增速度越快。式（5）利用共邻节点的入度和出度相似度影响节点间的相似关联程度，入度和出度相似度越大并且越具有对称性，节点间相似性越强。为了计算方便，将ST(i，j)的取值范围归一化为[0,1]，取值变化如图2（a）所示。假如简单照搬余弦相似度算法，ST(i，j)会考虑取值为Sin(i，j)、Sout(i，j)中的任意一项，或者不考虑边权方向而直接相加后纳入计算，算法会忽略边对称性、方向性等因素所产生的作用，导致计算结果准确度不高，共邻节点对相似度的贡献差异不能充分地表现出来，以此来评估相似度会降低计算结果的有效性。

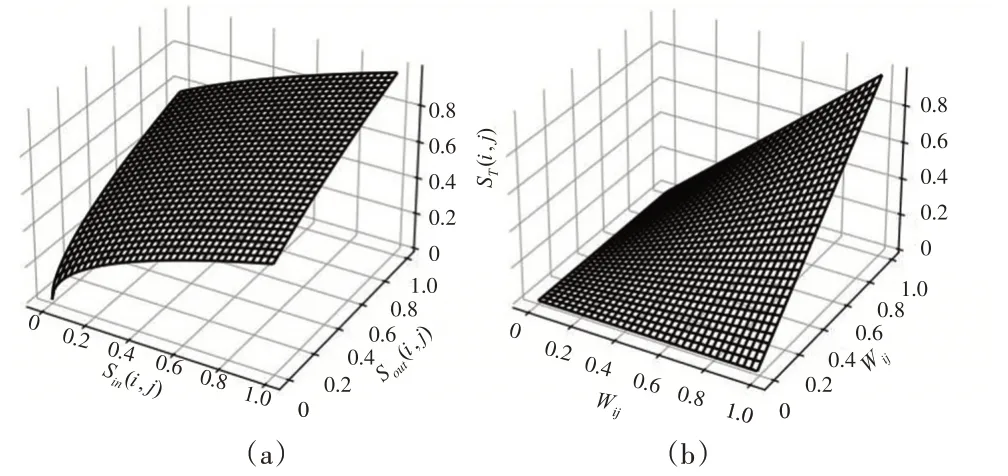
图2 共邻相似度与直连相似度的取值变化趋势

步骤2：计算两个节点的直连相似度LT(i，j)，沿用步骤1的算法思路，如式（6）所示。

其中，Wij和Wji分别为节点对之间直连两个方向的边权值，两者乘积反映LT(i，j)的直连相似度。两个边权值越不对称，LT(i，j)值变化幅度越大，越接近于0，其取值变化如图2（b）所示。如果依据其他常用的相似度计算方法，LT(i，j)直接被认为等于0，忽略了其对节点相似度的影响。

步骤3：计算两个节点之间的相似度S(i，j)，直接采用ST(i，j)和LT(i，j)两者的平方平均数求得，如式（7）所示。

上述公式具有以下特点：

（1）对于有向加权图，S(i，j)能较好地反映相邻节点个数、不同方向的相似度、节点间直连相似度、边权对称性等因素对两个节点相似度的综合影响。

（2）当两个节点不存在直接双向相连的包含节点间仅有单向连接的情况，即LT(i，j)=0 时，两个节点的相似度为，由共邻节点对两个节点在双向连接边权值的出度和入度相似度计算得出，通过比较与共邻节点的关系来确定相似性，与大多数文献提出的相似度算法思路一致。

（3）当两个节点存在双向相连并且无共邻节点时，ST(i，j)=0，两个节点的相似度减弱为。此时节点相似度由直连相似度决定，仅受两个节点直连边权值影响。

（4）当两个节点存在双向相连并且有共邻节点时，节点相似度由共邻相似度和直连相似度共同贡献所得。特别地，当两个节点间双向直连权值越不对称时，LT(i，j)递减变化幅度越大，对S(i，j)产生的影响程度越小，此时ST(i，j)起主导作用。

步骤4：基于上述算法设计，遍历所有空间位置节点，最终形成有向加权图的相似度邻接矩阵，如式（8）所示。

上述矩阵具有对称性，S(i，j)=S(j，i)，对角线元素全为0，非对角线元素表示节点对的相似强度。

3 基于相似度邻接矩阵的聚类分析

基于相似特性的邻接矩阵S进行谱聚类分析，算法步骤如下：

步骤1：按照式（9）获得标准化的拉普拉斯矩阵N。

步骤2：获取矩阵N的特征值和特征向量。基于矩阵N计算出以行向量存放的一维特征值矩阵λ和以列存放的特征向量矩阵F，F的每一列fi（i=1，2，…，n）代表一个特征向量。

步骤4：聚簇划分。将F''中的每一行作为一个k维的样本，共n个样本，聚类维数为k，对这些新生成的样本点进行K-means聚类，聚成k类，最后输出聚类结果，得到不同聚簇划分。

4 实例验证

为了验证本文相似度算法的有效性和合理性，本文以真实的高校学生生活和学习数据集作为实验对象，按照上文的相似度算法构建邻接矩阵，采取谱聚类后从节点聚集模块度、轮廓系数等方面进行对比分析。

4.1 数据集介绍

数据集1：高校学生消费群体由各类人群构成，群体中成员具有不同的饮食习惯，对不同商户的消费物品产生不同程度的偏好，消费物品在质量、服务、价格、口味等方面各异，吸引不同人群在商户之间进行选择性消费，消费者在商户之间发生马尔科夫链转移现象。学校以此来探询各商户分布结果是否具有更优的合理性，并预测相似经营商户间的关联程度，为学校优化餐饮质量提供决策参考。本实验采用华中师范大学一卡通系统的刷卡消费数据集，涉及校园卡用户数量为54243个，其中，2022年3月至6月消费流水总记录为93951622条，每条记录选取学生学号、商户标识、消费物品名、消费时间等作为实验数据参考点，其中消费物品名与商户标识绑定。为了减少消费量极小的商户对分析结果产生干扰，流水记录总数低于1000条的商户被过滤掉，最后进入分析的有效商户数量有167个。消费流水总记录100万次以上的商户占11.98%，50万～100万次的商户占34.13%，10万～50万次的商户占43.11%，10万次以下的商户占10.78%，能在最大程度上反映出用户对商户形成的选择性消费趋势。将上述商户标识用vi（i=1，2，…，167）表示，得到有167 个节点的状态空间。依据式（2）将商户间的消费活动关系转化为有向加权图，图中每一条方向线表明当前商户vi的消费群体向另一个商户vj转出的概率Pij。状态空间的商户间转移次数越多，转移关系权重就越大。

数据集2：高校学生选修公选课时因课程热度或个人需求不同出现选课次数互转现象，采用以此形成的选修课聚簇分布来评估课程间的相关性、紧密性及相似热度，方便学校教务部门及时了解公选课开设情况，并且要求评估的算法要具备比较高的准确度。实验数据来源于华中师范大学2014—2023年的学生选课系统数据集，有效的选课记录有2283226条，参与分析的课程有294门，参与选课的学生有44548位，在选课记录中选取学生学号、课程代码、学期标识、选课时间等参与分析。将上述学生选课活动的课程标识记为vi（i=1，2，…，294），共有294 个节点的状态空间。依据式（2）将选课活动关系转化为有向加权图，图中每一条方向线表明选修课程vi的学生群体向另一门课程vj转出的概率Pij。

4.2 聚类模块度对比

为了评价本文算法对实例数据集节点的划分质量，引入聚类模块度进行分析。一般来说，聚类模块度值越大，则对应的社区聚类个数越准确，并且更加接近真实的社区结构分布情况。以数据集1和2为例，分别选取BDMS、文献[6]相似度、余弦相似度，按照本文谱聚类分析步骤进行实验对比，聚类模块度比较结果如表1和表2所示。经过多次对商户节点进行聚类合并后，当数据集1和2的聚类数量分别被划分为2～5 个和2～7 个时，BDMS 结合谱聚类分析获得的聚类模块度值大于0.3，且高于对比算法。在聚类个数为3～10 个时，文献[6]相似度和余弦相似度的聚类模块度值都明显低于本文算法的计算结果。综上所述，BDMS 结合本文谱聚类算法在相似性度量及聚簇划分上优于对比算法，具有发现潜在的学生活动社区网络节点的分布的能力。

表1 数据集1相关算法聚类模块度比较

表2 数据集2相关算法聚类模块度比较

4.3 聚类结果轮廓系数对比

聚类结果的轮廓系数是聚类的密集与分散程度的评价指标[19]。从轮廓系数评价算法原理可知，其取值范围为（-1，1），且其值越接近于1，代表聚簇内聚集度和聚簇间分离度效果越优。通过评价指标不仅可以评估相似度计算针对不同聚类算法的有效性,而且还可以很好地了解给定有向加权图的节点动态关系。针对数据集1 和2，将BDMS谱聚类与BDMS、余弦相似度、文献[6]及文献[7]相似度等进行K-means聚类对比实验，同时检验BDMS算法采用传统聚类分析的效果。聚类数k在2～30 取值，计算过程获取一系列聚类的轮廓系数参与比较，结果见图3。

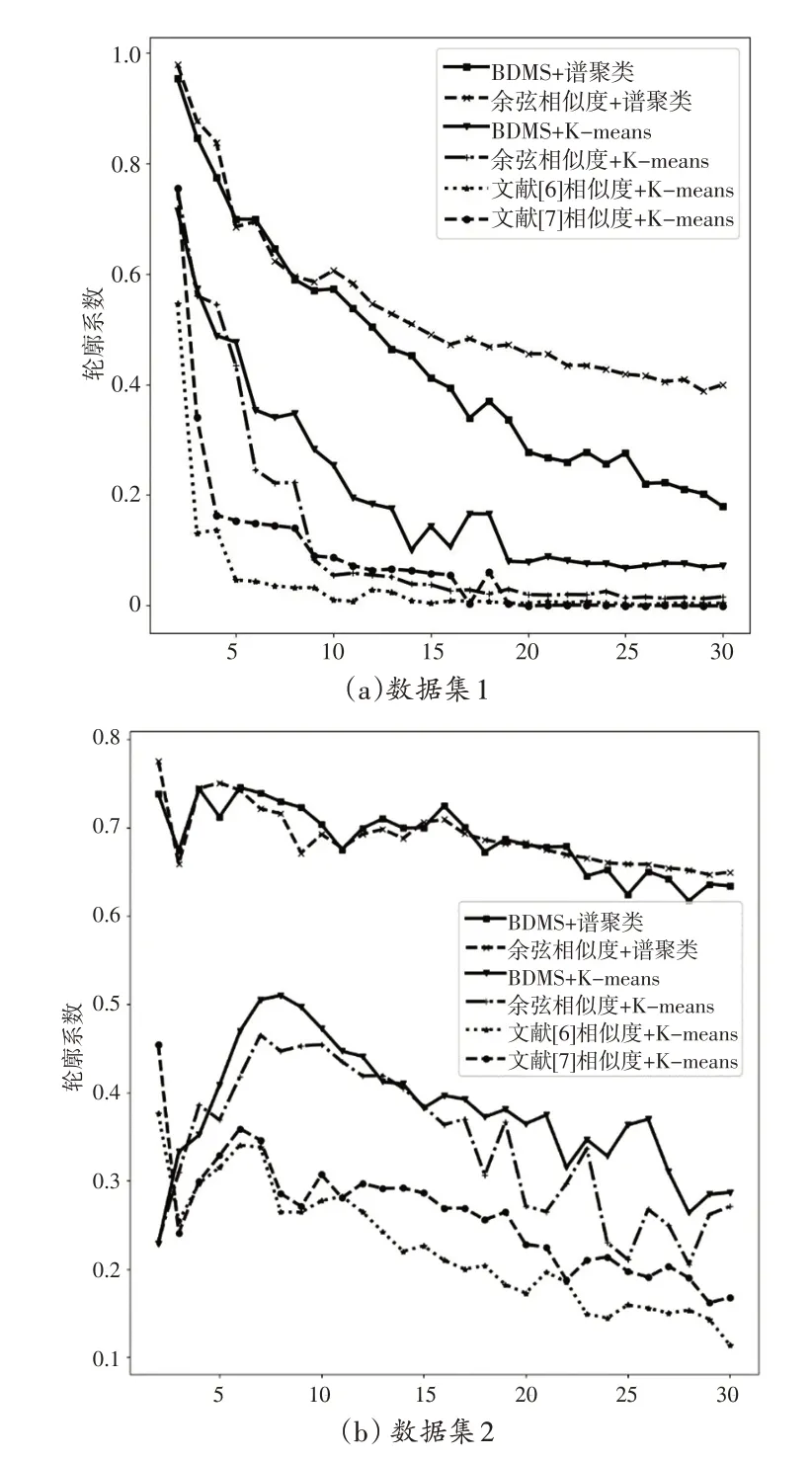
图3 不同相似度算法聚类结果的轮廓系数对比

从图3 中可以看出，本文BDMS 聚类结果的轮廓系数在最优时分别达到0.9534、0.7380，并且从整体上来看，不同聚类数的轮廓系数也明显高于其他四种计算方式（不含余弦相似度+谱聚类），结果显示，采用BDMS 结合谱聚类分析时对社区聚簇划分具有较大优势。

进行K-means 聚类时，相比于余弦相似度、文献[6]和文献[7]提出的相似度算法，BDMS算法得到的轮廓系数从整体上看平稳性相对较好。虽然文献[6]考虑到有向加权图的边权和边方向信息，文献[7]提出以用户参与同一事件次数越多和参与事件类别越多为条件，分别建立无向图相似度模型，但当处于不同聚类数时，聚类结果的轮廓系数相对偏小。另外，针对余弦相似度采用谱聚类分析，根据图3（a）和（b）的结果，其轮廓系数分布比较接近采用BDMS进行谱聚类分析的计算结果，但是与表1和表2中的聚类模块度相比，两者聚类划分的评估结果差别较大，表明该方法不推荐在谱聚类中使用，而BDMS却能很好地适应谱聚类和传统K-means聚类的分析。

5 结论

本文以社区活动形成的有向加权图为研究对象，设计了一种双向度量相似度的计算方法，并采用谱聚类无向切图实现社区聚簇的最优划分，将有向加权图节点划分问题转化为无向加权图聚类问题。通过理论和实例分析，得出如下结论：

（1）BDMS算法思路简单。依托马尔科夫链现象存在的节点转移关系，算法提取较少的样本信息即可构建有向加权图，比较容易实现。

（2）BDMS算法能在很大程度上真实体现节点间的相似关系。算法综合考虑了影响计算结果的诸多因素，并将各种因素的合理性在计算中体现出来，节点间关系的表示与实际接近。

（3）相比文中其他相似度算法，BDMS 算法结合谱聚类无向切图，在聚类分析时输出结果准确度高，能够更好地发现潜在的社区结构，同时在谱聚类和传统K-means聚类分析中表现出很好的适应性，并且在高校学生数据集的实例验证中验证了其有效性。为更充分地利用节点相似度进行快速聚簇划分，后续还可在子图内节点聚集质量和进一步优化算法方面开展工作。