“四层四环”育人模式在数学教学中的应用研究

黄如琳　唐剑

摘 要：基于刘英琦提出的“四层四环”育人模式，分析学生对基本不等式的“经验性理解”“本质性理解”“结构性理解”“文化性理解”四个理解层次，以“学科理解与单元规划”“学习者分析、教学目标与评价设计”“任务设计与学科实践”“后测与师生教学反思”四个教学环节开展“基本不等式”教学活动，探究该模式在高中数学中的推广应用.

关键词：“四层四环”育人模式；基本不等式；深度理解

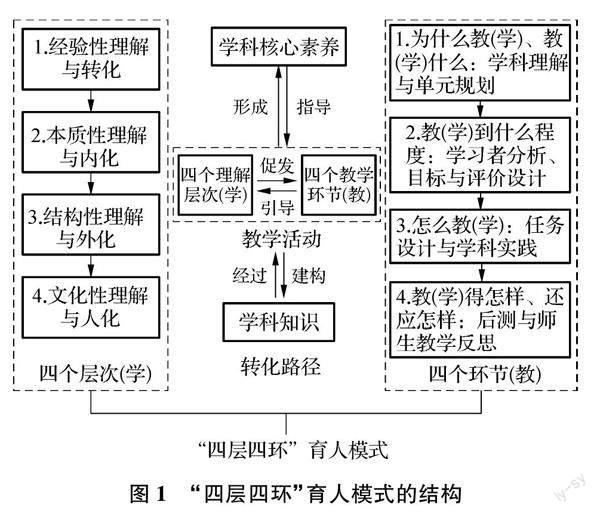
“双减”背景下，随着课堂教学的深入改革，在全国范围内掀起了探究适应学科核心素养发展的教学模式的浪潮.深圳市教研专家刘英琦提出了指向核心素养发展基于学生深度理解的综合教学模式——“四层四环”育人模式，其基本结构见图1，该模式从“教”和“学”两个维度双向建构，突出教学过程各要素的动态综合与系统协作.本文以“基本不等式”为例，来研究“四层四环”育人模式在数学教学中的实践应用.

1 学科理解与单元规划

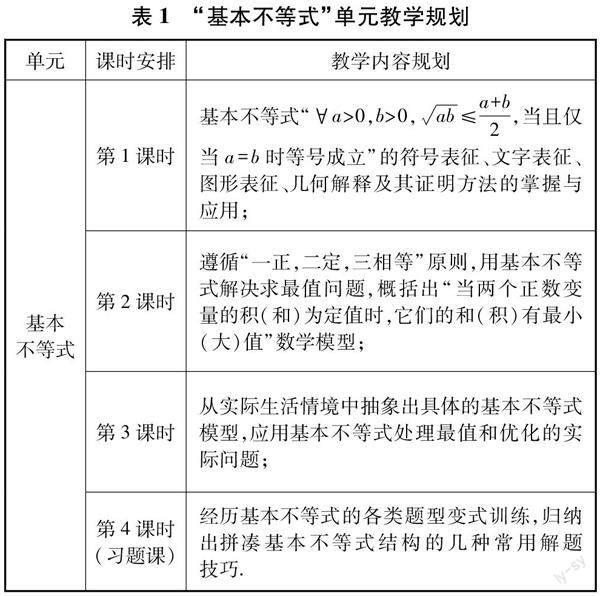
章建跃提出“理解数学是教好数学的前提，理解数学、理解学生、理解教学是数学教学质量的根本保证，是教师专业化发展的基石”.何为“基本不等式”？本质上是正实数的基本运算（加、减、乘、除、乘方、开方）所引起的大小变化，它的结构反映了两个正实数的几何平均数和算术平均数之间的大小关系.方亚斌整合了对基本不等式的十几种认知视角强调对数学本质的认识，其“基本性”体现在与几何、代数、方程、函数、统计、向量、复数等数学知识间的内在联系，同时它还具备证明多种形式不等式、解决最值问题的工具性.基于学科理解，表1将“基本不等式”核心内容类单元总共规划为4个课时：

2 学习者分析、教学目标与评价设计

2.1 学习者分析

高一学生不仅学过圆的性质和相似三角形，有从赵爽弦图中发现勾股定理的学习经验，适应由“形”及“数”的探究方法，对数形结合思想并不陌生；由于初中就已经熟练掌握了一元一次不等式的解法，具备不等式基本的运算化简能力，并能解决相应的实际问题；前置课程学习的不等式性质是证明基本不等式的理论依据.

2.2 教学目标

2.3 教学评价

（1） 通过从几何图形问题情境中抽象出基本不等式，并获得它的几何解释，诊断学生对基本不等式的经验性理解；

（2） 利用重要不等式、几何法、作差比较法、分析法、综合法推导出基本不等式，運用基本不等式证明其他不等式，诊断学生对基本不等式的本质性理解以及对多种证明方法的应用；

（3） 通过在具体实例中运用基本不等式数学模型求最值，经历变式训练能灵活拼凑基本不等式结构解决各类问题，评价学生对基本不等式的结构性理解；

（4） 通过从现实生活情境中抽象出基本不等式数学模型处理最值和优化的实际问题，感受基本不等式的优美结构和应用价值，用数学的眼光看问题，发展学生对基本不等式的文化性理解.

（4） 考查数学阅读和数学写作的开放性主观题.举例：结合本节课学习和课外资料收集，请从不同角度谈谈你对基本不等式的理解.

4.2 师生教学反思

学生的学习反思：对课堂听课的认真程度作自我评价；总结在小组讨论基本不等式证明方法过程中的收获；表达自己对基本不等式的理解并让同学作出评价；反思课后作业中错题的原因，分门别类地制作错题集；自我规划并监测学习过程等等.学生反思属于元认知学习策略，有利于培养多角度、多方法分析问题的思维方式，将所学的知识技能内化为关键能力、核心素养以及数学观，以达到理解的最高层次——文化性理解.

教师的教学反思：通过分析学生的四个理解层次反思自身对学科的深入理解程度，“知其然知其所以然”才能“传道授业解惑也”；经历第一课时的实操反思“基本不等式”单元规划的合理性，发展数学整体教学观；通过课堂提问、随堂测试、课后作业等过程性评价反思教学评是否达到一致性，是否落实了学科核心素养的发展；根据教学效率来判断对学情掌握的准确度，适应学生的最近发展区才能使数学知识自然流畅地发生与发展；通过分析后测结果，在得到真实反馈的基础上反思教学任务的达成情况，以便改进教学的不足之处，总结有效的教学策略，积累宝贵的教学经验，促进教师自身专业发展.

基金项目：安徽省研究生教育教学改革研究重点项目（项目编号：2022jyjxggyj344）;阜阳市教育局—阜阳师范大学基础教育“双减”专项研究项目（项目编号：2021SJZX028）.