非等温粗糙表面液滴撞击特性试验与仿真研究
岳出琛, 戴庆文, 陈 磊, 黄 巍, 王晓雷
(南京航空航天大学 直升机传动技术重点实验室, 江苏 南京 210016)
近年来,我国航空航天事业的飞速发展对高端装备制造提出了更高要求.航空发动机轴承腔常采用油雾润滑系统[1-3],循环油雾为轴承提供有效润滑和冷却,油雾撞击腔体的演变过程会直接影响系统润滑和冷却性能,深入理解固体表面油滴碰撞的动力学行为对其设计至关重要[4].此外,液滴撞击固体表面的铺展动态和热量传递行为在飞机抗结冰、抗结霜[5-7]、冷凝与传热[8-10]等领域也有广泛应用.
国内外学者对液滴碰撞开展了大量研究.对于理想光滑表面液滴碰撞行为,Rioboo等[11-12]观察了水滴在光滑表面撞击产生的快速、冠状飞溅等现象,并指出低表面张力促进液滴产生冠状飞溅,黏度增大会抑制液滴发生形变.液滴碰撞行为与其理化性质紧密相关,Du等[13]研究了多类型硅油及丙三醇的撞击特性,发现液滴初始扩散行为主要由惯性力以及黏性力支配,铺展时液膜最小厚度与韦伯数和接触角无关.对于液滴碰撞后的动态行为,陈石等[14]对液滴受力状态进行分析,得到惯性力、黏性力和表面张力系数的表达式,指出液滴振荡时最大铺展直径、高度与液滴尺寸、初始铺展速度正相关,与表面张力负相关.对于液滴在固体斜壁面碰撞行为,刘登等[15]指出前铺展因子分别与入射角和液滴直径的变化趋势呈负、正相关,后铺展因子与前铺展因子规律相反.基体浸润性也会影响液滴的碰撞行为,Almohammadi等[16]探究了液滴在亲水、疏水表面撞击时液滴边界的飞溅现象,发现疏水表面上液膜抬升体积、液滴形变程度均大于亲水表面.而对于基体为非平面的固液碰撞现象,Abolghasemibizaki等[17]利用平整、弧形超疏水表面进行试验,结果表明液滴在弧面的接触时间小于平面,且速度增大后液滴在弧面更易产生对称式破裂.
光滑表面液滴碰撞研究充分展现了液滴的撞击特性,然而在实际工况中,液滴撞击粗糙表面更为普遍,且粗糙表面并非等温.Aboud等[18]利用不同倾斜度粗糙表面对液滴撞击时前进端形貌及撞击产生的次级液滴进行对比,发现液滴在光滑表面的动态形貌非对称性远大于粗糙织构表面,并将其归因于底部受空气对液滴铺展的抑制作用;Yuan等[19]基于格子Boltzmann算法模拟了液滴在非等温粗糙表面上的撞击行为,指出减小偏度并控制峰度在3°左右是提高液滴回弹能力的有效方法.此外,大量非等温表面液滴碰撞的研究聚焦于Leidenfrost现象,Liu等[20]探究了水滴在100~280 ℃基体表面的撞击现象,绘制出液膜的沸腾曲线及蒸发区域,并指明Leidenfrost温度受到基体表面粗糙度的影响;Bernardin等[21-22]系统地阐述了液滴在高温固体表面上的主要沸腾模式及固体表面Leidenfrost温度的主要影响因素;这为受热固体表面的液滴碰撞行为研究提供了一定参照.
尽管国内外科研人员对液滴在粗糙表面的撞击特性展开了探索,但仍有需要进一步完善之处,如,目前相关研究中涉及的粗糙表面较为理想化,无法有效体现实际工况下的固液碰撞现象;受热固体表面的液滴撞击研究对象主要是水,而有关润滑油的研究却鲜有报道.同时,考虑到航空发动机内部腔体温度以及粗糙度分布不均匀现象普遍存在,故研究油滴在非等温粗糙表面上撞击时所涉及的铺展、飞溅和弹跳等一系列行为具有重要意义.
鉴于此,本研究中选择了硅油及类似发动机内部腔体表面的非等温粗糙表面开展固液碰撞研究,重点探索了硅油黏度、撞击速度、液滴初始直径、金属表面粗糙度及温度对硅油撞击特性的影响.研究表明,撞击速度、基体表面温度及油滴初始直径对硅油最大铺展直径均呈正相关,基体表面粗糙度、硅油黏度呈负相关.基体温度对油滴形貌影响较小,但随温度升高,尾迹残留现象愈发明显.仿真结果较好的模拟了试验过程并揭示了液滴撞击的演变机制,相关研究工作为理解液滴在非等温粗糙金属表面的撞击行为提供了丰富的理论和试验依据.
1 试验方法
1.1 材料选择
固体材料.为贴近真实工况,试验选用了几种表面粗糙度不同的试样进行研究.其中,光滑试样是长宽高为75 mm×30 mm× 3 mm、经打磨抛光处理(Ra=50±5 nm)的316不锈钢块;粗糙试样为面粗糙度Ra为6.3、12.5和25 μm的三种经抛喷丸处理获得的标准样块.图1所示为利用白光干涉仪拍摄的上述三种不同表面粗糙度样块的表面二维形貌、三维形貌以及截面轮廓曲线.将轮廓曲线数据导入COMSOL Multiphysics软件可以获得包含不同粗糙度表面的二维模型.
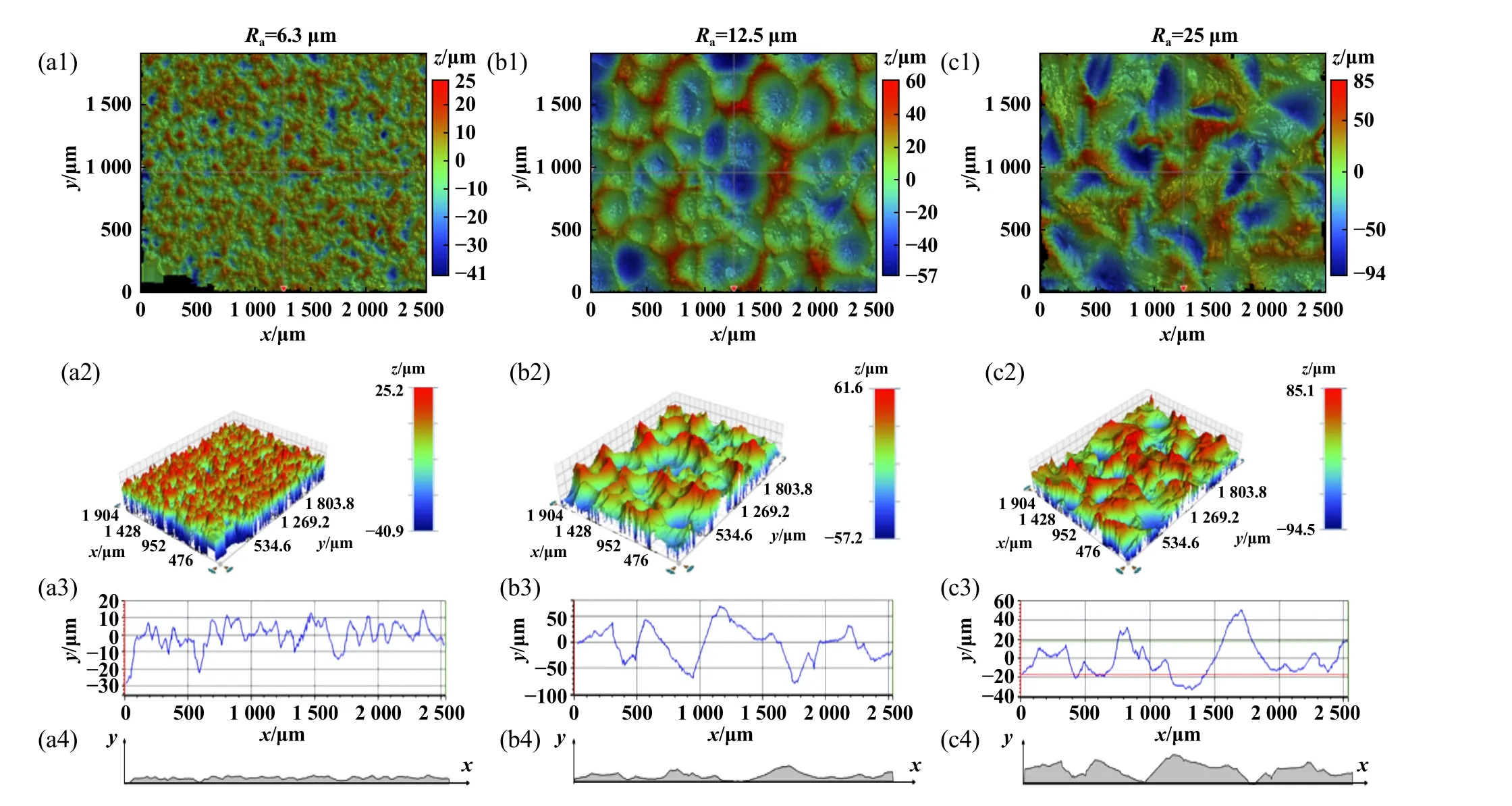
Fig.1 Performance characterization of different rough surfaces: (a1~c1) two-dimensional surface topography; (a2~c2) threedimensional surface topography; (a3~c3) profile altitude curve; (a4~c4) two-dimensional model in COMSOL Multiphysics and the horizontal and vertical coordinates show the two-dimensional shape of the model图1 不同粗糙表面的性能表征:(a1~c1)二维表面形貌;(a2~c2)三维表面形貌;(a3~c3)剖面海拔曲线图;(a4~c4) COMSOL Multiphysics中的二维模型及其在横纵坐标下对应的二维形貌
液体材料.硅油因其良好的理化性质和热稳定性在航空航天领域得到广泛应用[23],本研究中选用二甲基硅油作为撞击试验所使用的液体材料,其物性参数列于表1中;此外,选用去离子水(密度为1 000 kg/m3,表面张力为71.97 mN/m)进行对比试验.

表1 二甲基硅油物性参数Table 1 Physical property parameters of silicone oil
1.2 试验装置及步骤
本试验在自主搭建的液滴撞击观测平台进行,其结构如图2所示.试验装置主要由支架、注射器、加热平台、三脚架、高速相机(i-SPEED 726R, iX Camera, UK)及光源组成.液滴体积通过不同规格的注射针头来调节,通过调整注射器的高度来改变撞击速度,基体表面温度由核心部件为PTC陶瓷加热芯的加热平台精准控制.试验环境为室温25 ℃,标准大气压强.具体试验步骤如下:将基体试样分别置于丙酮溶液、95%乙醇中超声清洗5 min,再放入去离子水中洗净并用氮气吹干;设置基体表面温度使其稳定在预定值(表2);根据自由落体公式:h=V2/2g,[V、g分别为速度、重力加速度(9.8 m/s2)],换算获得指定碰撞速度下注射器的高度;随后缓慢推动注射器使液滴无初速度自由落体,拍摄记录全部过程(帧率10 000 f/s),并对视频分析处理,获得相应的试验数据.图2插图所示为硅油在50 ℃光滑不锈钢表面的撞击行为,其中比例尺根据拍摄时所设置的参照物而绘制.
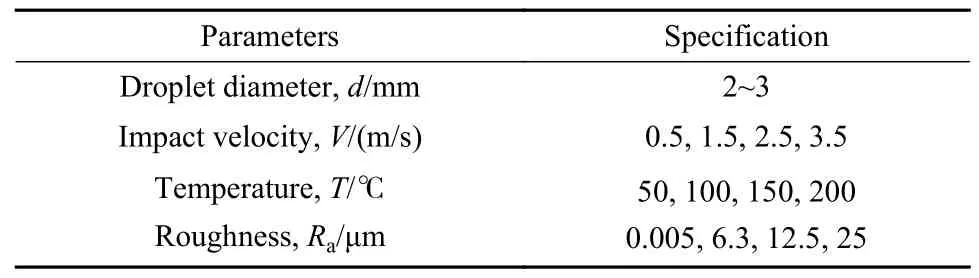
表2 试验条件Table 2 Test conditions
2 数值仿真
随着近年来计算机技术的快速发展,各类多物理场仿真软件,如ANSYS、COMSOL Multiphysics等,逐渐成为学者进行科学研究的有效工具.鉴于COMSOL Multiphysics软件高效的物理场耦合性能及优异的计算能力,因此本研究选用此软件进行数值模拟.针对研究中固液接触、液体流动以及固液气热传递等现象,在仿真时采用三种多物理场(两相流、马兰戈尼效应和非等温流动)进行模拟.
2.1 控制方程
流体传热物理场通常用来模拟流体界面间的热传递,因此适用于本仿真试验中液滴与空气的热量交互.该物理场模型中所有区域均为可活动域,即区域具有流体的属性,其传热方程为
式中:U为速度矢量,q为热通量向量,Q即热源,ρ、Cp、k分别表示液体密度、定压比热容、流体导热系数,∇为向量微分算符.
层流界面主要基于一般形式的Navier-Stokes方程来计算层流状态下单相流的速度和压力,其中包含了质量守恒连续性方程(式3)、动量守恒向量方程(式4)及能量守恒方程(式5)[24]:
式4中:P为压力,τ、F分别为黏滞应力张量、体积力矢量,I为动量矢量.式5中:R为应变速率张量,其计算公式为
水平集方法是一种用于界面追踪和形状建模的数值模拟技术,该方法将自由液面的表面张力引入Navier-Stokes方程,并利用高阶函数Φ来追踪两相流模型中的气液界面[25]:
式中:γ为重新初始化参数,ε为界面厚度控制参数.当Φ=0时,当前流体与流体1属性相同,当Φ=1时,当前流体与流体2属性相同,在气液交界面上其值为0.5.密度和动力黏度的水平集函数分别为
式中:ρ1、ρ2分别为流体1、流体2的密度,μ1、μ2分别为流体1、流体2的黏度.因此,通过追踪Φ的数值即可随时查看气液交界面的变化状态.
由于常温液滴接触高温基体后其内部产生温度梯度,故引入非等温流动多物理场可将层流物理场和流体传热物理场进行有效耦合.同时鉴于固液间常见的马兰戈尼对流现象,因此在模型中添加马兰戈尼效应:
式中:n为某方向的单位矢量,t为当前时间.液滴内部温度发生变化即会导致表面张力改变,根据Dai等[26]对硅油表面张力随温度变化的试验结果,本文中设定模型中硅油表面张力的变化规则为
式中:γ(T)为硅油在当前温度T时的表面张力、γ(T0)=20.8 mN/m表示硅油在参考温度T0=20 °C下的表面张力.同时,引入液体动力黏度与温度间的关系式[27]
式中:μ0、μ(T)分别为参考温度T0、温度T时的动力黏度,b=0.02414为黏温系数.对于基体,设底边为润湿壁,其控制方程为
式(13)中:nwall为壁面某处的方向单位矢量,式(14)中:Ffr为固液间摩擦力,β为滑移长度;式(15)中引入Fθ以控制固液接触角.
2.2 二维模型
设直径为2 mm的自由液滴被空气包裹在1个10 mm×3 mm的二维矩形空间中[图3(a)],环境温度为25 ℃.为保证计算效率,采取较细化网格剖分后的二维模型如图3(b)所示.对于两种流体,气体采用COMSOL Multiphysics中的空气默认属性,硅油参数列于表1中.
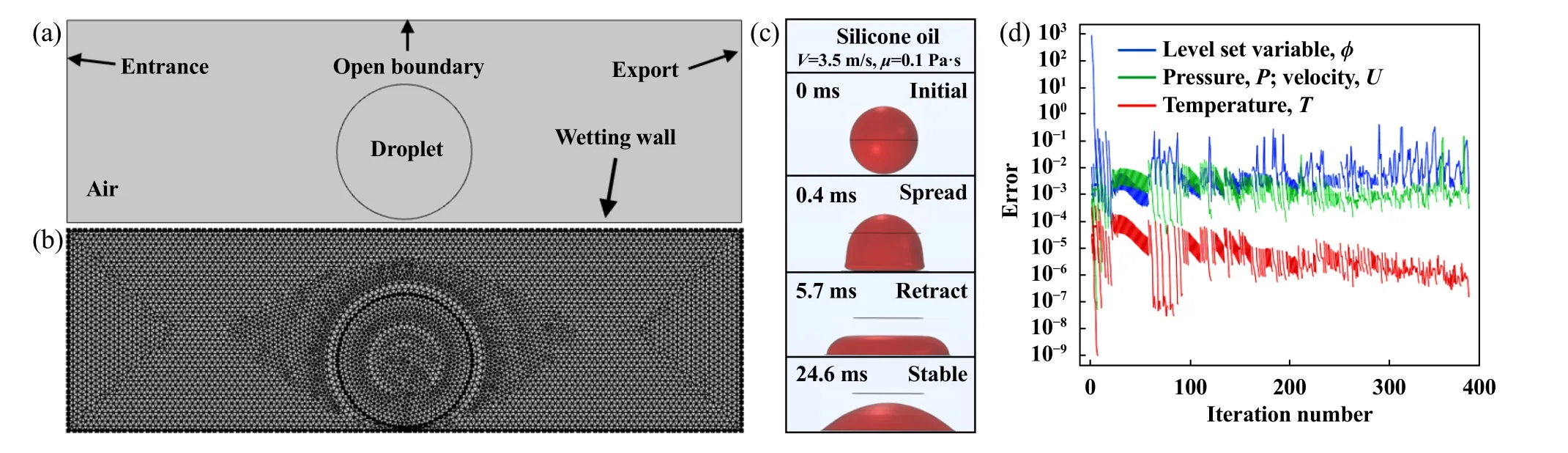
Fig.3 (a) Two-dimensional model and boundary conditions, (b) mesh generation, (c) simulation results of silicone oil droplet impact behavior in Figure 2, (d) error diagram of separated solver图3 (a) 二维模型及边界条件,(b)网格剖分,(c)图2中硅油撞击行为的仿真结果,(d) 分离式求解器误差图
2.3 边界条件
假设固液间无反应,壁面温度恒定,液滴为不可压缩流体且流体流动符合层流流动规律[28].构建二维模型后取其左侧为压力入口(p=0),右侧为压力出口(p=0),顶部为开放边界[图3(a)].图3(c)所示为图2中液滴撞击行为的仿真结果,可以看出试验及仿真中液滴形貌以及变化趋势相仿,由分离式求解器误差图[图3(d)]可知数值模拟结果误差较小且收敛性良好.
3 结果与讨论
3.1 硅油/水在光滑不锈钢表面的撞击行为
图4所示为μ=100 mPa·s的硅油油滴与水滴在50 ℃光滑不锈钢表面分别以0.5、2.5和3.5 m/s撞击后的行为对比.由图4(a~b)可知,随着撞击速度的提升,油滴与水滴的铺展直径均呈快速增大的趋势,但相同条件下油滴在各时间节点的铺展直径均小于水滴.这是因为在扩散阶段液滴的运动主要由惯性力驱动,初始动能一部分转化为表面能,另一部分以克服自身黏性力的形式被耗散.鉴于硅油黏度远大于水,所以前者在扩散过程中存在更大程度的黏性耗散,因此铺展直径较小.观察图4(c)可明显看出油滴达到最大铺展直径后的回缩程度远小于水滴,且水滴表面液体流动较为湍急,形貌变化大.这是由于回缩阶段液滴的运动由表面张力主导,储存的表面能转化为动能,且回缩过程依旧伴随黏性耗散,故水滴比油滴展现出更加剧烈的撞击行为.
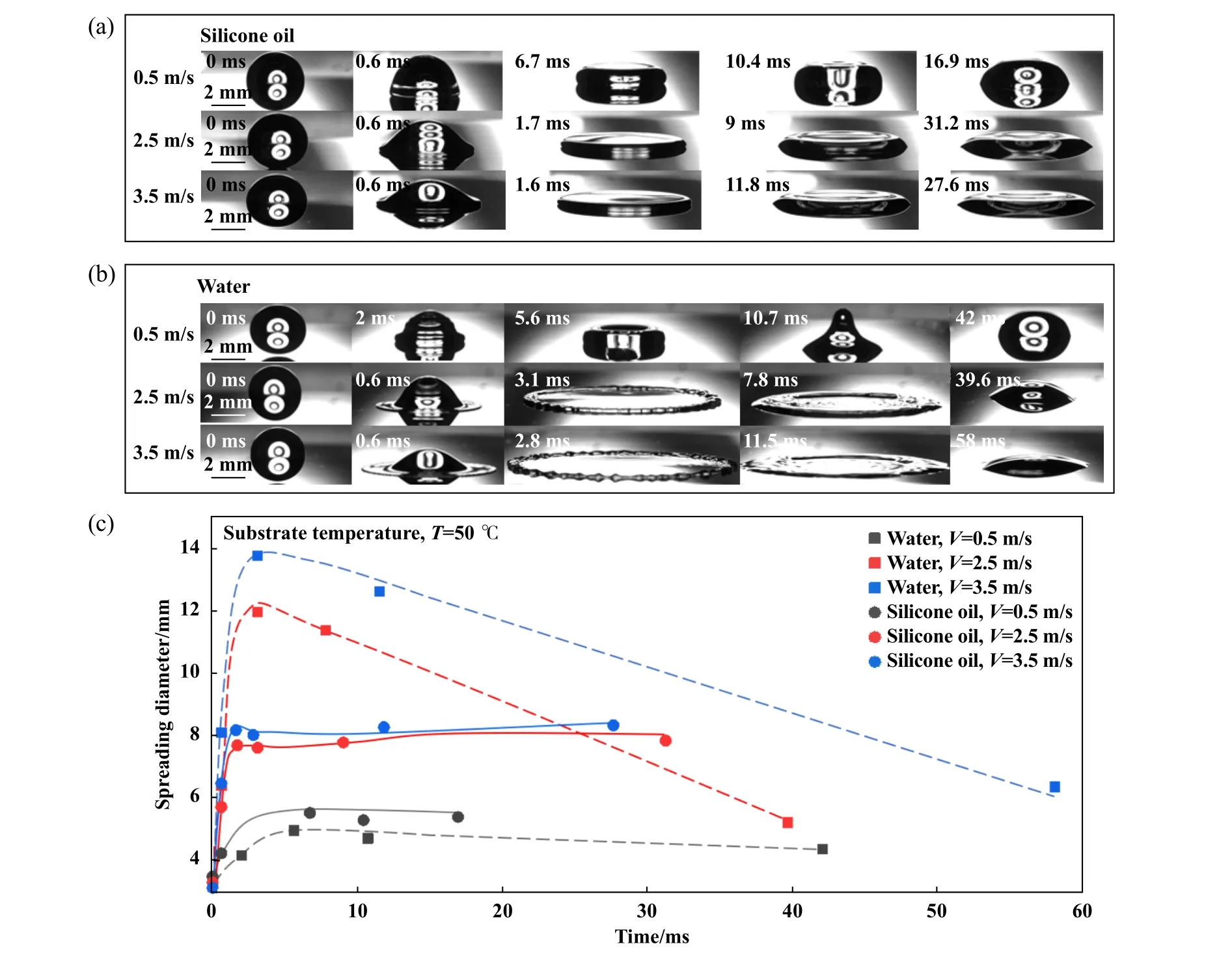
Fig.4 (a) Impact behavior of silicone oil droplets, (b) impact behavior of water droplets, (c) relationship between droplet spreading diameter and time which was measured experimentally图4 (a)硅油油滴的撞击行为,(b)水滴的撞击行为,(c)试验测得液滴铺展直径与时间的关系
本小节主要针对液滴的整体形貌变化进行讨论,由上文所述可知硅油的形貌变化较为稳定,且黏度类型多样,考虑到最大铺展直径Dmax是分析液滴铺展特性的重要指标,因此在下文中对影响硅油撞击特性的相关因素及Dmax集中开展对照试验进行研究.
3.2 硅油黏度对撞击行为的影响
为探究硅油黏度对其撞击行为的影响,选取黏度为100、500和1 000 mPa·s的硅油以3.5 m/s速度在50 ℃光滑不锈钢表面进行撞击试验,并利用软件对其撞击行为进行模拟,结果如图5所示.由试验结果可知,在铺展阶段,不同黏度硅油达到最大铺展状态的时间分别为1.7、1.2和0.6 ms,呈下降趋势.回缩过程中,μ=100 mPa·s的油滴顶部收缩较为明显,在24.6 ms到达稳定状态.而对于另外两种黏度的硅油,由于顶部无凹陷,仅铺展边界收缩后就到达了稳定状态[图5(a)].结合仿真结果也可看出油滴的撞击剧烈程度与黏度呈负相关[图5(b)],这再次印证了前文所述黏性力对液滴运动的抑制作用.
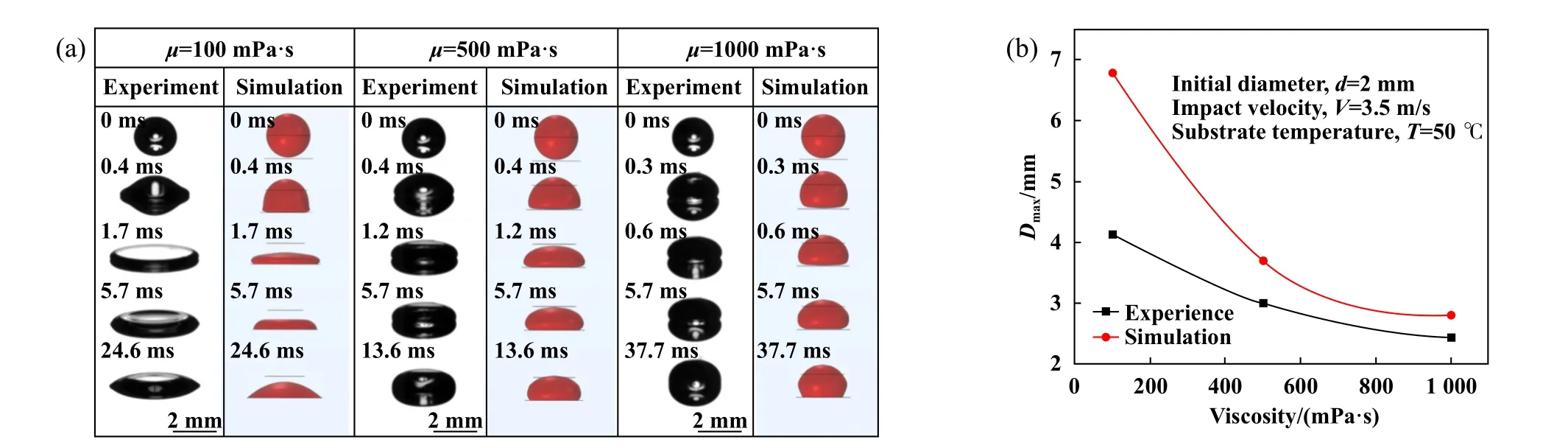
Fig.5 (a) Experiential and simulation results of silicone oils with different viscosities impacting on a 50 °C smooth stainless steel surface, (b) relationship between viscosity and maximum spreading diameter图5 (a) 不同黏度硅油撞击50 ℃光滑不锈钢表面的试验及仿真结果,(b) 黏度与最大铺展直径的关系
对于试验与仿真结果间的误差,综合考虑各条件后本文中作出如下解释:(1)接触角滞后效应会减慢油滴在基体上的铺展速度,但仿真中并未考虑该效应;(2)仿真中的二维模型与实际三维模型存在一定系统误差,建立三维模型虽可提升精度,但计算时间大幅增加;(3)仿真时所用表面虽由真实表面重构获得,但其与真实表面依然存在差异.因此,上述误差导致图5(b)中油滴在仿真时的铺展程度大于实际情况.
3.3 硅油初始直径及撞击速度对撞击行为的影响
图6(a)、(b)分别展示了不同初始直径(μ=100 mPa·s,V=3.5 m/s)、不同撞击速度(μ=100 mPa·s,d=2 mm)的硅油油滴在50 ℃光滑不锈钢表面的撞击现象.由图6(a)可知虽然初始直径不同,但撞击过程皆分为铺展阶段和回缩阶段,且在最大铺展状态时,油滴中部向下凹陷,四周隆起.不同的是,随着直径增大,油滴达到最大铺展状态的时间由1.7增至2.2 ms.相比于增大前,油滴的相对变形程度并没有大幅提升,这是由于动能增量并不能大幅抵消黏性耗散带来的负面影响,形貌变化依旧受限.由图6(b)可知,随着撞击速度的增加,最大铺展直径Dmax由3.9增至4.1 mm,液滴形貌变化相仿.

Fig.6 Impact behavior of oil droplets under different conditions: (a) different initial diameters;(b) different impact velocities图6 不同条件下油滴的撞击行为:(a)不同初始直径;(b)不同撞击速度
液滴撞击固体表面时,液滴物理性质、撞击条件对撞击行为的影响可以用一系列无量纲数,如惯性力与表面张力的比值——韦伯数(We)、惯性力与黏性力的比值——雷诺数(Re)、表面张力与黏性力的大小关系——奥内佐格数(Oh)来衡量[29-33]:
式中:ρ为液体密度,V为撞击速度,d为液滴初始直径,γ、μ分别表示液体表面张力及黏度.由式(16)可知,We、Re不仅涉及液滴自身物理性质,还与撞击条件有关,而Oh仅受液滴自身物理性质影响.因此除前文所探究黏度影响外,撞击速度及初始直径也是液滴撞击行为的重要支配因素.
为了进一步说明Oh、We、Re和Dmax间的联系,图7(a)所示为四种撞击条件下Re与Dmax、Oh与We间的对应关系,可以看出Dmax与Re呈正相关,且相比于增大撞击速度,增大液滴初始半径对提升Dmax的影响程度更大.当Re介于28.8~67.4时,其对Dmax影响较小,但介于67.4~101.1时影响程度陡增,这也对应着图6(a)中两液滴较大的形貌差异.Oh主要受液滴直径的影响,故与Dmax无直接相关性.图7(b)所示为整合试验与仿真中不同液滴初始直径与撞击速度下的最大铺展直径与相应We而绘制的散点图及拟合曲线.由该图可知固定黏度时,改变惯性力后Dmax/d与We呈线性正相关,但在We增幅较大的情况下Dmax/d增值很小,这说明We对Dmax的影响较为有限.图7(b)中的误差来源与3.2节所述相同,仿真结果虽然略大于试验结果,但是基本趋势与其相仿.
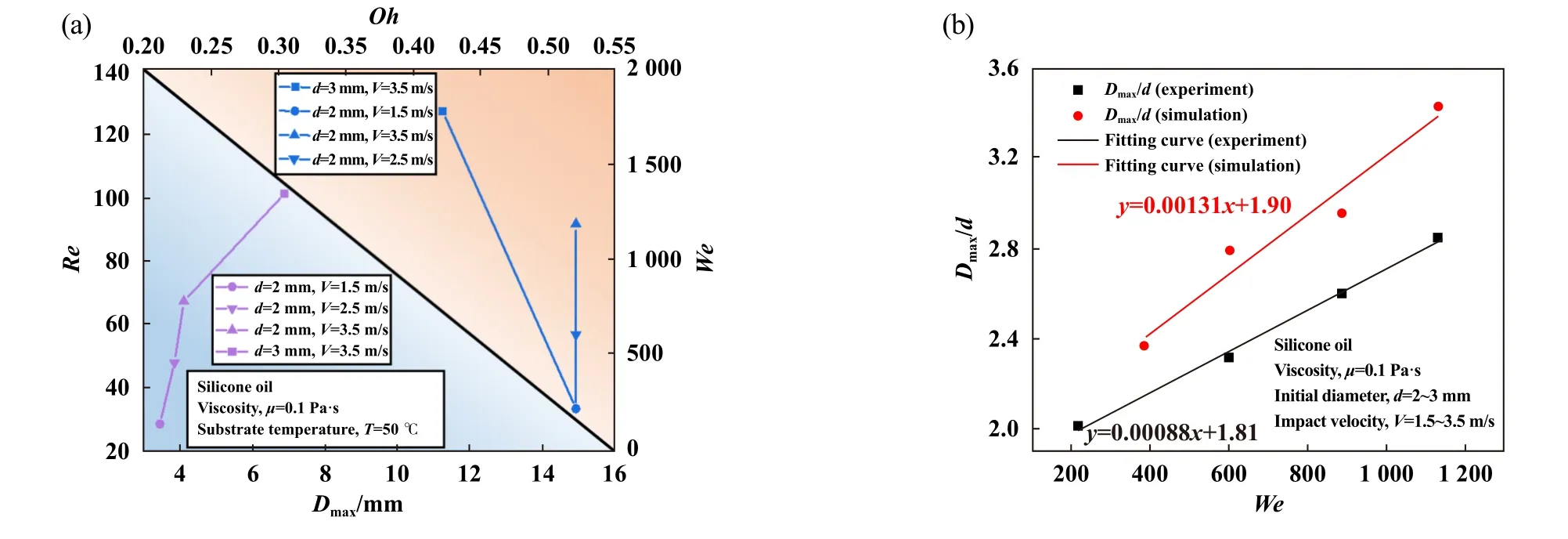
Fig.7 (a) Relationship between maximum spreading diameter of oil droplets and Oh, We and Re under different impact velocities and initial radiuses, (b) relationship between Dmax/d and We of oil droplets under different impact conditions图7 (a) 不同撞击速度、初始半径下油滴最大铺展直径与Oh、We、Re的关系,(b) 油滴在不同撞击条件下Dmax/d与韦伯数We的关系
图8(a~b)所示为图6(a)和(b)中油滴在0.0、0.2、0.4、0.6、1.0、1.5、2.0和3.0 ms及各自达到最大铺展时(对应时间分别为4.4、4.0和4.2 ms)的形貌仿真示意图,如图可知相同时间节点下d=3 mm时液滴的铺展速度更快,且前进端上扬幅度较低.图8(c)和(d)所示为对应图8(a)和(b)中油滴的前进端温度、单位面积的表面张力(γua)及铺展半径变化曲线图.由图8(c)可知,当油滴初始直径d=3 mm时,前进端温度浮动程度较大,这源于其撞击初期前进端单位面积的表面张力值较低,因此铺展速度较快[由图8(d)下部3条曲线在前期的斜率也可得相同结论]、边界液膜较薄,故而温度骤升;随着油滴进入稳定铺展阶段,边界液膜厚度适量增加,前进端与附近流体间的温差逐渐缩小.对于同初始半径,不同撞击速度的情况,结合图8(a)可知撞击速度越大,铺展速度即得到提升,前进端厚度越低,因此受热面积增大,升温较快.考虑到前进端某点的位置在油滴铺展时不断变化,故温度曲线并非呈单一变化趋势,且根据式(11),对比图8(c)和(d)即可看出图8(a)和(b)中所标出的前进端点对应的温度与单位面积表面张力呈负相关趋势.由图8(d)可知,当d=3 mm时油滴单位面积的表面张力值较低,结合铺展直径变化曲线斜率可知其铺展速度较快;当d=2 mm时,尽管撞击速度由2.5 m/s提升至3.5 m/s,但铺展直径的提升程度稍差于增大初始直径.
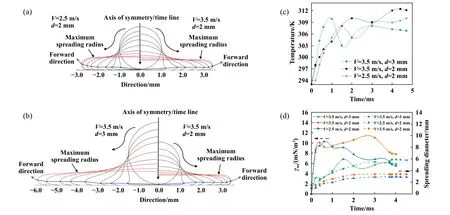
Fig.8 (a) Simulation comparison diagram of oil droplets spreading at each time point under different impact velocities, (b)simulation comparison diagram of oil droplets spreading at each time point under different initial diameters, (c) temperature change curves at the forward direction under different conditions, (d) variation curves of spreading radiuses and surface tension per unit area at the forward direction with time under different conditions图8 (a)不同撞击速度下油滴在各时间点铺展仿真对比图,(b)不同初始直径油滴在各时间点铺展仿真对比图,(c)不同条件下前进端温度变化曲线,(d)不同条件下前进端单位面积的表面张力及铺展半径随时间的变化曲线
3.4 基体表面温度对撞击行为的影响
为进一步探究基体温度对油滴撞击行为的影响,图9(a)和(b)分别展示了黏度μ=100 mPa·s,初始直径d=2 mm,撞击速度V=3.5 m/s的油滴在不同温度光滑不锈钢表面的撞击行为及其最大铺展直径与温度的关系.由图9(a)可知随着温度升高,在0~5.7 ms内,各油滴的形貌并未出现较大差异,但对比最终稳定状态可看出油滴边缘形貌由尖锐逐渐变得圆滑,即回流作用导致的残留尾迹现象越发明显.
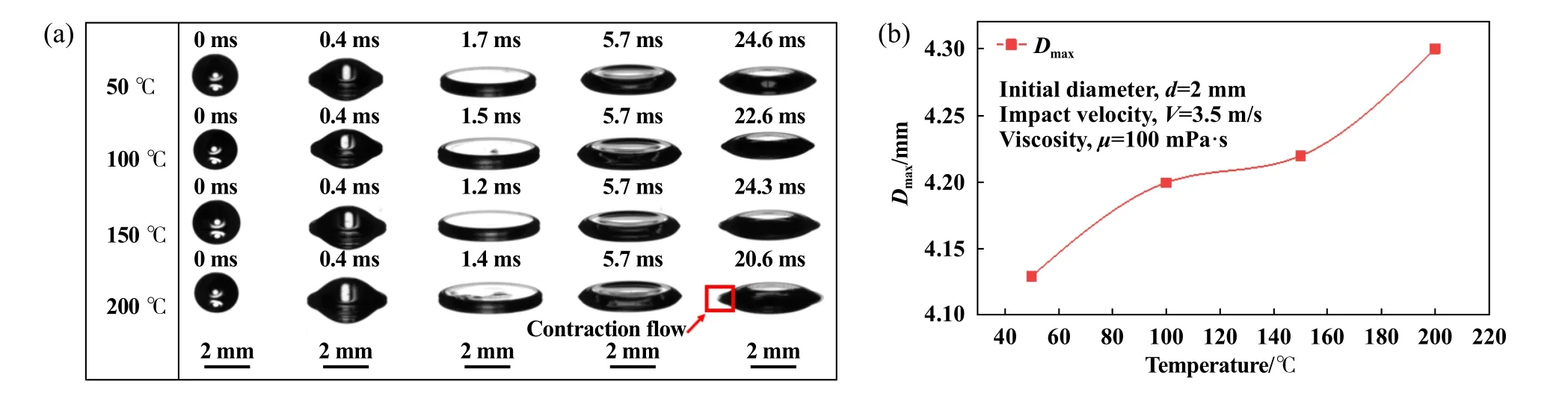
Fig.9 (a) Impact behaviors of oil droplets on smooth stainless steel surface at different temperatures, (b) relationship between maximum spreading diameter and temperature图9 (a)油滴在不同温度光滑不锈钢表面的撞击行为,(b)最大铺展直径与温度的关系
从图9(b)中可知基体温度对油滴最大铺展半径影响程度较低,而这主要是由固液间传热时间较短导致的.油滴与高温不锈钢表面接触后会产生热量交换,但其内部温度不会突变[34-35].固液传热时间是指固液从开始接触直到无温差所需要的时间.传热时间尺度τthermal可通过热扩散系数来估算:
式中:hl为液滴高度,κ为热扩散系数(硅油约为1.5 mm2/s).将最大铺展状态的油滴看作圆饼,根据液滴体积守恒则有:
式中:Dmax平均值约为4.2 mm;d为初始直径,τthermal约为60 ms.试验中各油滴在不同温度基体表面平均铺展时间约为1.5 ms左右,远小于传热时间尺度,故油滴撞击时热量来不及传递到内部便已达到最大铺展状态.因此,当基体表面温度从50 ℃上升到200 ℃时,油滴在表面的铺展速度以及最大铺展直径几乎一样.
总体而言,表面温度对液滴撞击的影响主要体现在回缩阶段.5.7 ms时,200 ℃下油滴顶部相比于50 ℃有着更小的顶部半径,这说明其回缩速度更快,且其回缩时间相比于50 ℃缩短了近4 ms.图10所示为50和200 ℃下油滴达到稳定状态时底部液体流动状态及内部仿真速度场,可明显看出200 ℃下油滴底部有较为显著的内缩现象且内部流速更大,并残留了尾迹.这是由于油滴内部不均匀的温度梯度导致其表面产生表面张力梯度,从而在内部产生由边缘向中心的Marangoni流动,进而促进回缩.因此,随着基体表面温度的增加,油滴收缩现象会更明显,但由于自身黏滞效应影响,边界液膜无法快速回缩,以至于产生尾迹.
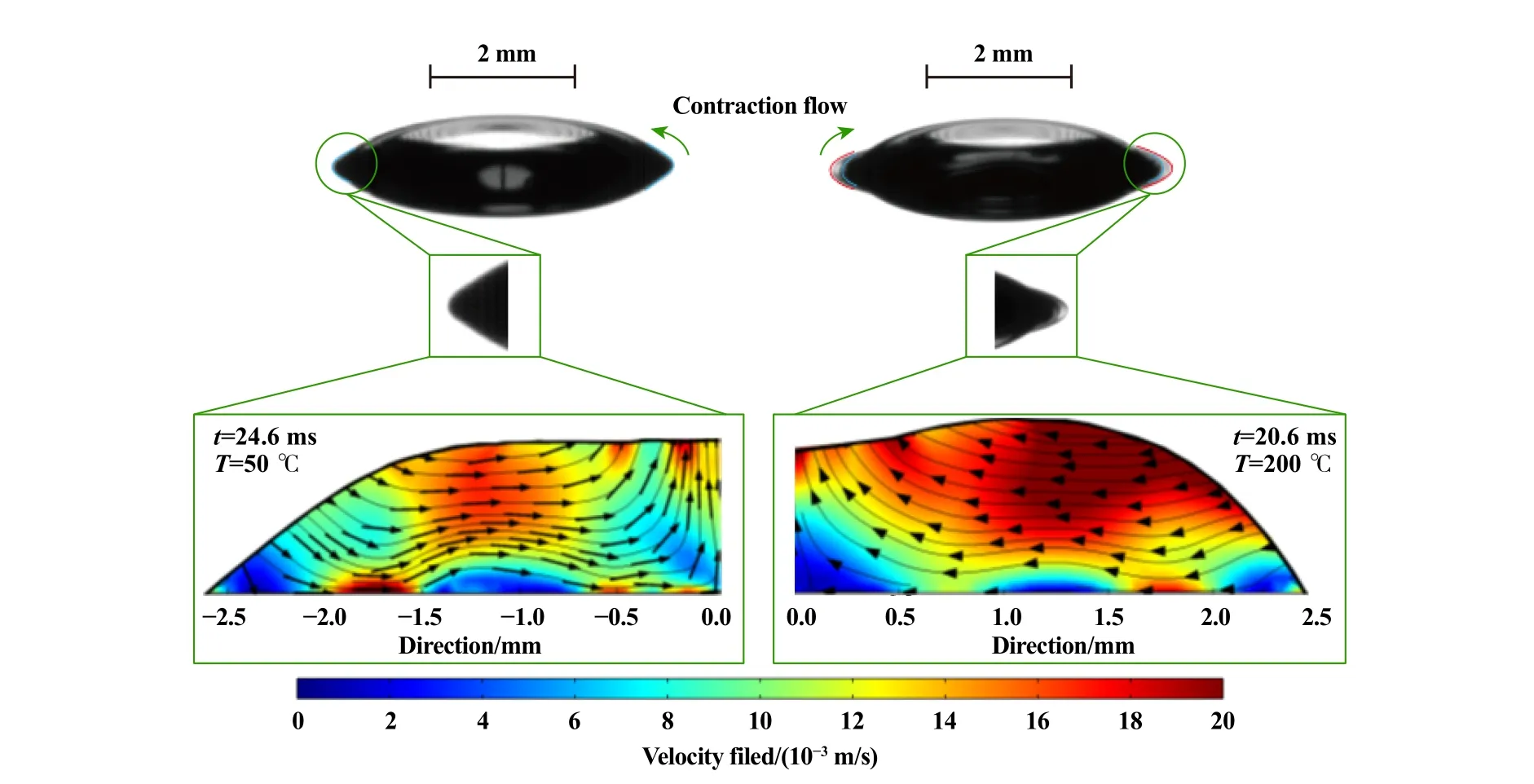
Fig.10 The bottom liquid flow state and internal simulation velocity fields of oil droplets when reaching 50 ℃and 200 ℃ stable states图10 50 ℃、200 ℃下油滴达到稳定状态时底部液体流动状态及内部仿真速度场
针对固液间热交换现象,图11所示为油滴(μ=100 mPa·s)以速度2.5 m/s撞击四种不同温度表面的仿真状态.对比可知,各时间节点下油滴内部温度分布较为均匀,相比于50、100、150和200 ℃时油滴内部表面张力矢量分布更为密集,表明内部温度梯度更大.结合图11(e)中各条件下前进端黏度的变化曲线可看出0.2~2 ms时黏度迅速降低,对应于图11(a~d)中此时间段内油滴内部较大的温度梯度;而2 ms时油滴已接近最大铺展状态,固液间温差较小,所以黏度衰减趋势开始变缓.因四种表面温度下油滴黏度变化均处于同一量级,故各条件下油滴最大铺展直径相仿.
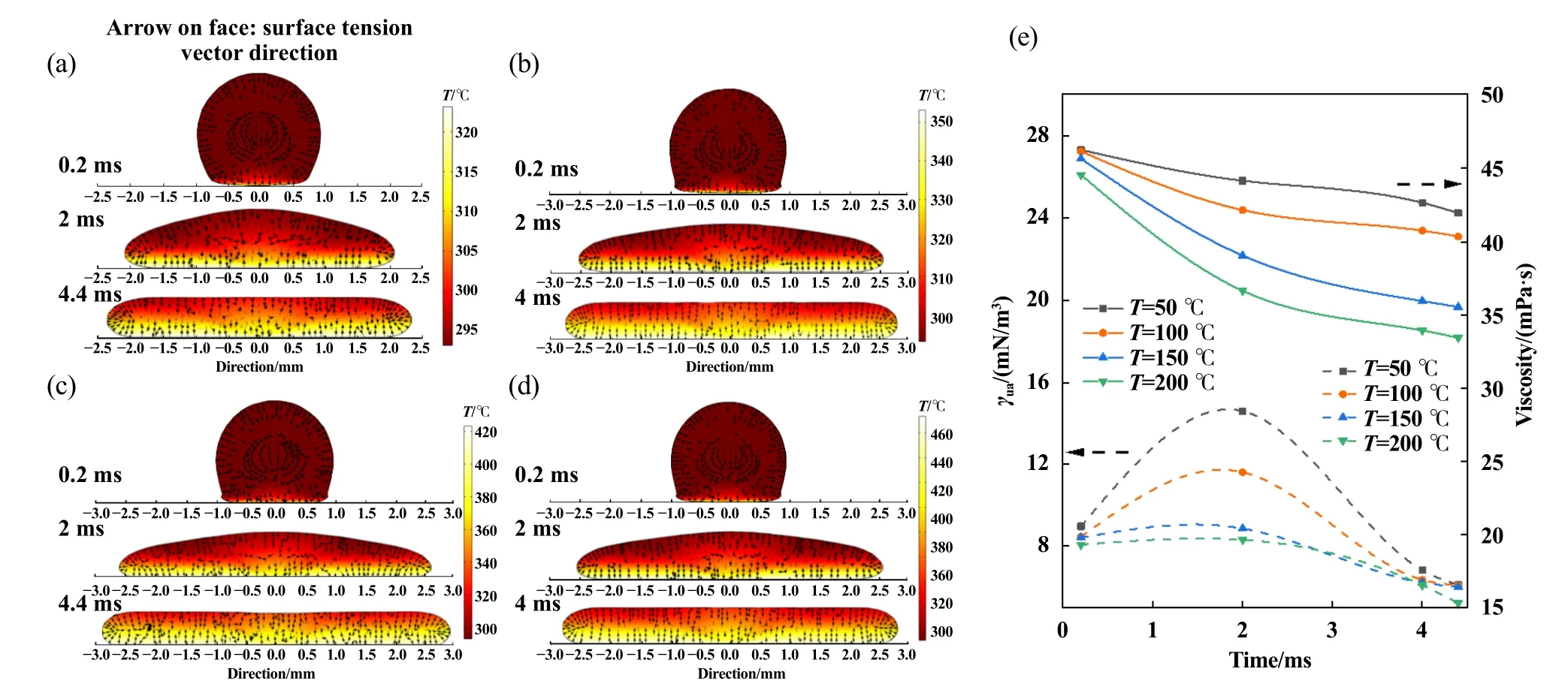
Fig.11 Comparison of impact dynamics and internal surface tension vector distribution of oil droplets on surfaces at different temperatures: (a) T=50 ℃; (b) T=100 ℃; (c) T=150 ℃; (d) T=200 ℃; (e) change curves of viscosity and surface tension per unit area at the forward direction when oil droplets impact on surfaces at different temperatures图11 油滴在不同温度表面的撞击动态及内部表面张力矢量分布对比:(a) 50 ℃;(b) 100 ℃;(c) 150 ℃;(d) 200 ℃;(e)油滴在不同温度表面撞击时前进端单位面积的表面张力及黏度变化曲线
3.5 基体表面粗糙度对撞击行为的影响
图12所示为硅油油滴(μ=100 mPa·s,V=3.5 m/s)在不同粗糙度不锈钢表面(T=50 ℃)的实际撞击行为及仿真结果.从时间上来看,油滴实际撞击平均铺展时间为2.46 ms,比光滑不锈钢表面要滞后0.76 ms左右.油滴平均回缩时间为6.14 ms,约为同条件下光滑不锈钢表面的1/4.随着表面粗糙度的增加,油滴的高度逐渐降低,底部铺展直径不断提升,而在最大铺展状态,随着表面粗糙度的上升,最大铺展直径呈小幅下降趋势,结合仿真结果也可验证此规律.

Fig.12 Actual impact behaviors and simulation results of oil droplets on stainless steel surfaces with different roughness图12 油滴在不同粗糙度不锈钢表面的实际撞击行为及仿真结果
图13更加直观地展示了油滴在0.0、0.2、0.4、0.6、1.0、1.5、2.0和3.0 ms及各自达到最大铺展(4.4、4.3、4.3和4.3 ms)表面粗糙度对油滴铺展行为的影响.在黏度μ=100 mPa·s、撞击速度V=2.5 m/s、基体温度T=50 ℃的条件下,由图13(a~b)可知随着表面粗糙度(Ra)增至6.3和12.5 μm,各时间段油滴前进端与底面的间距持续增加,而Ra=25 μm时呈现先增后减的趋势.在图13(c~d)中,除光滑表面外其余三种情况下油滴的前进端温度、铺展直径演变及最大铺展直径相仿,但与光滑表面相差较大.这种现象主要是由油滴在基体表面铺展时润湿状态的转变所引起.
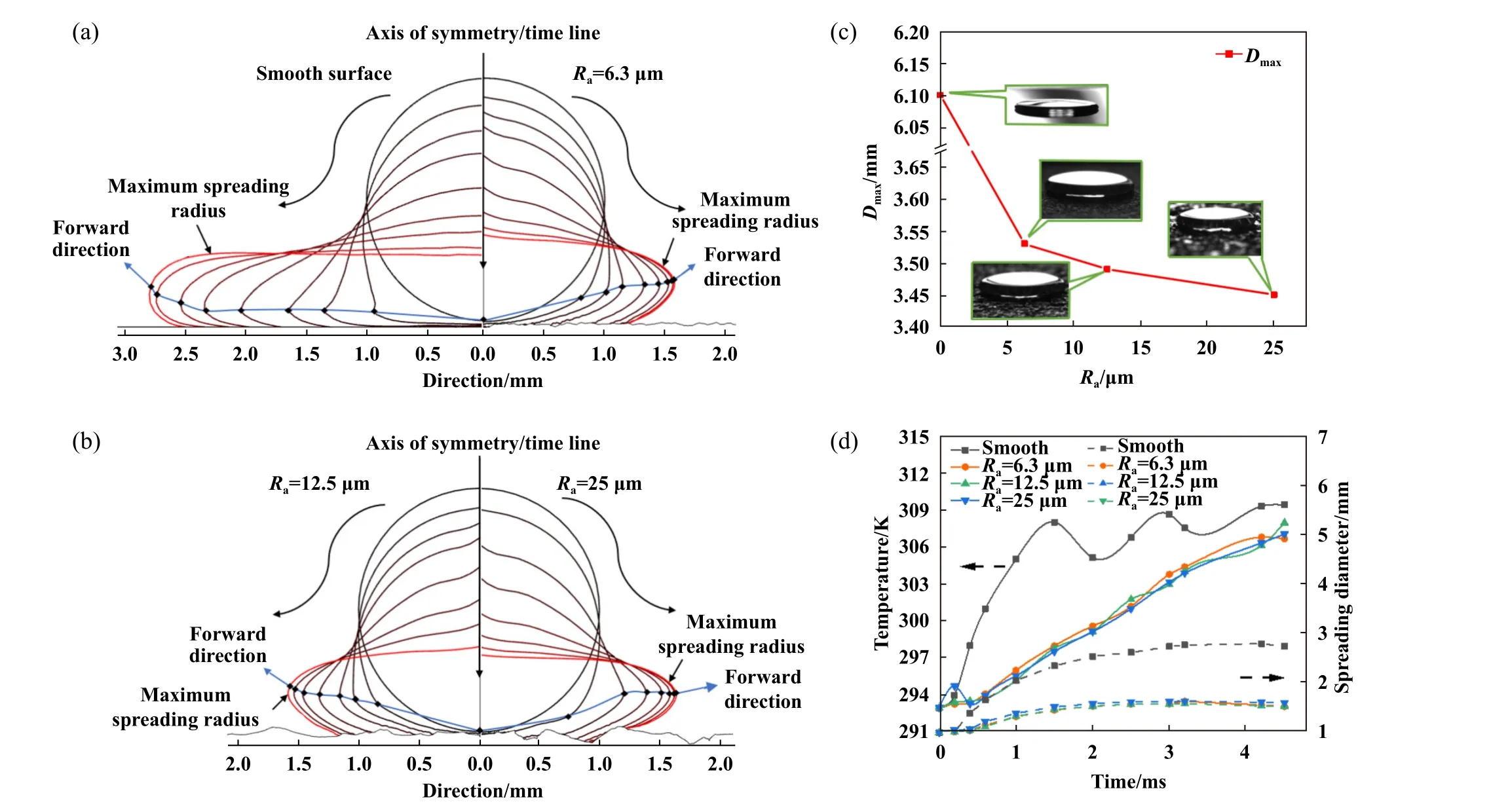
Fig.13 (a) Spreading simulation of oil droplets impacting on smooth surface and Ra=6.3 μm surface in each time period, (b)spreading simulation of oil droplets impacting on Ra=12.5 μm and Ra=25 μm surface in each time period, (c) the relationship between maximum spreading diameter and surface roughness, (d) the relationship between spreading radius, forward direction temperature of oil droplets and time图13 (a) 油滴在光滑表面与Ra=6.3 μm表面的各时间段铺展仿真,(b) 油滴在Ra=12.5 μm与Ra=25 μm表面的各时间段铺展仿真,(c) 最大铺展直径与表面粗糙度的关系,(d) 油滴扩散半径、前进端温度与时间的关系
研究表明,液滴在粗糙表面的润湿状态主要有两种,即Wenzel状态和Cassie-Baxter状态[36-38].液滴撞击到粗糙表面后,在粗糙结构的间隙中会拘禁部分空气,此时固液之间并未完全接触,呈现Cassie-Baxter状态.随着液滴继续向下运动,由于粗糙结构的阻碍,流体会在相邻粗糙结构之间形成弯液面,并继续向下填充间隙,直至填满.此时,固液界面完全接触,达到Wenzel状态,因此液滴在粗糙表面上的铺展行为就可以看作无数个弯液面向下移动将间隙填满的过程[39].这个过程往往伴随着能量消耗,而随着表面粗糙度增大,间隙变得越来越大,所以铺展所需的能量也随之增多[40-42].
从黏性力的角度来看,液滴铺展时固液接触线单位长度上所受的黏性力可以通过下式计算[43]:
式中:θ为稳定接触角,θadv为前进接触角.粗糙不锈钢表面呈亲油性,液滴稳定在Wenzel状态时存在θ=θw,且有:
式中:ζ为粗糙度因子,表示实际接触面积与名义接触面积之比,θY为杨氏接触角.因此对于图14(a)中的光滑表面,油滴具有较好的浸润性,在铺展过程中内部黏性力为阻碍其运动的主要因素;当液滴撞击到较粗糙表面[图14(b)]时,需要消耗部分体积来填充空间间隙以实现进一步铺展,且此时表面粗糙结构的分布对其铺展产生一定的阻碍作用;而面对粗糙表面[图14(c)]时,严重的体积耗散成为阻碍液滴铺展的主导因素,且不同形貌的粗糙结构导致油滴铺展时θ以及θadv不断变化,很大程度上对油滴铺展方向产生未知影响.由式(18)可知油滴所受黏性力随表面粗糙度的增大而增大,因此黏性耗散程度提升,进一步对油滴的铺展产生负面影响.
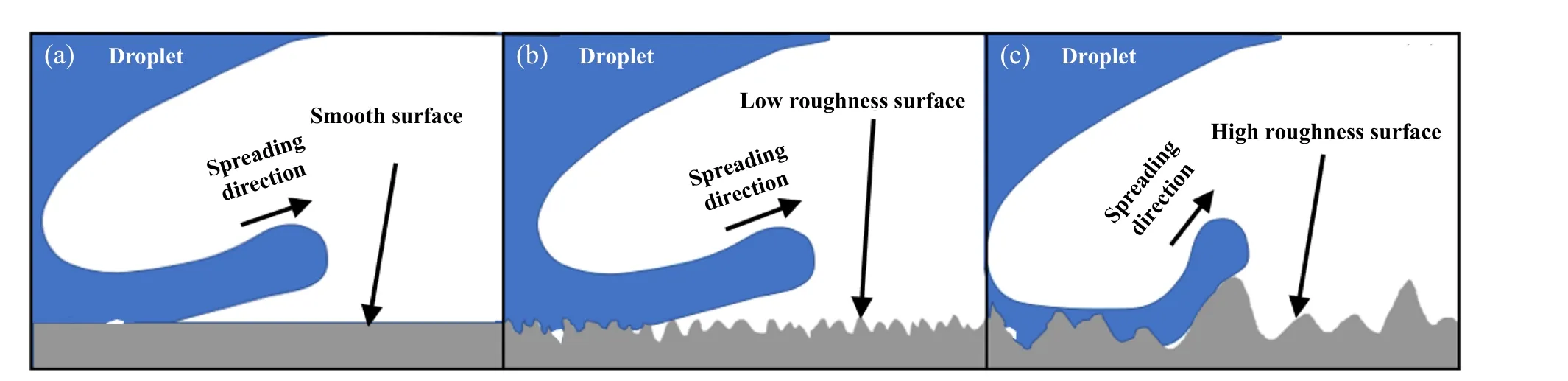
Fig.14 Wetting phenomena of droplets on different surfaces: (a) smooth surfaces; (b) low rough surfaces; (c) high rough surfaces图14 液滴在不同表面的润湿现象:(a)光滑表面;(b)较粗糙表面;(c)粗糙表面
4 结论
本研究探究了硅油在不同特性金属表面的撞击行为及差异,并予以理论分析.基于COMSOL Multiphysics多物理场仿真软件,着重分析了硅油黏度、撞击速度、液滴初始直径、金属表面粗糙度及温度对硅油撞击行为的影响.根据试验结果可得出以下结论:
a.相比于水滴,硅油油滴撞击光滑不锈钢表面时的变形程度较小,且随着硅油黏度的提升变形程度进一步减小.随着油滴直径增大,油滴在铺展和回缩阶段的直径均大幅增加,但达到最大铺展状态的时间小幅提升.
b.撞击速度的增大为油滴提供更多动能,因此在一定程度上促进了油滴的铺展.但由于黏性耗散的存在,导致油滴铺展、收缩过程中损失较多能量,因此不同油滴的撞击动态差异较小.
c.油滴在不同温度表面的撞击动态大体相仿,但尾迹残留现象随温度的升高而愈发明显.改变基体表面粗糙度(6.3~25 μm)对油滴的铺展行为影响差异较小,各时间节点铺展直径、前进端温度相似,但与光滑表面有一定差距.

