聚四氟乙烯真空摩擦学性能的分子动力学模拟

吕文静, 刘 建, 赵 盖, 王利涛*, 吕 美,*

(1.济宁医学院 药学院, 山东 日照 276826;2.中国科学院兰州化学物理研究所 固体润滑国家重点实验室, 甘肃 兰州 730000;3.南京航空航天大学 机械结构力学及控制国家重点实验室, 江苏 南京 210016)

随着空间科学的发展，聚合物空间摩擦学引起了人们广泛的研究兴趣.2010年，我国飞船舱外空间材料试验，发现空间环境对固体润滑材料的摩擦学性能产生明显影响.王齐华所在课题组利用地面模拟试验研究了空间环境对聚合物材料的影响，发现空间环境可以改变聚合物的微观结构、化学组成和表面形貌，进而影响其力学性能和摩擦学性能[1-8].尽管空间暴露试验和地面模拟试验的实际价值非常高，但其成本过高，限制了全面系统研究.理论研究者建立了可以预测环境因素与材料相互作用的理论模型，例如可以确定辐照粒子对材料损伤程度的Monte Carlo方法[9-13]，可以评估真空热循环效应的二维有限元模型[14]，可以预测原子氧辐照侵蚀的Banks掏蚀和量子力学模型[15-20]，以及可以从微观角度分析分子链内部的相互作用机制的分子动力学模拟[21-23].

郑菲所在课题组前期通过地面模拟装置研究了真空度对聚四氟乙烯(PTFE)和聚酰亚胺(PI)摩擦学性能的影响，发现两者摩擦系数随着真空度的增加逐渐降低，磨损率受真空度影响较小[24-25].本研究通过分子动力学模拟来研究真空度对PTFE摩擦学性能的影响，希望能为前期的试验结果提供一定的理论计算支持.

本研究中建立PTFE与铁原子层滑动摩擦的分子模型并进行模拟计算，获得了PTFE在不同真空度条件下的摩擦系数和磨损率，系统分析了摩擦过程中PTFE分子链和对偶铁原子层之间的径向分布函数、温度变化、相对浓度以及沿厚度方向的速度变化，揭示了不同真空度下PTFE分子和铁原子之间的内在机理，为研究聚合物材料的真空摩擦学性能提供技术指导和理论方法.

1 试验部分

1.1 材料模型的建立与优化

首先，利用分子动力学模拟软件Material Studio建立聚合度为50的C2F4重复单元，基于蒙特卡洛规则，选择10条分子链构建了43 Å×43 Å×43 Å的PTFE无定形模型，如图1所示.为了得到能量最低以及结构更加合理的PTFE材料模型，需要对初始模型进行几何优化和动力学平衡.采用COMPASSⅡ力场，该力场是第一个基于从头计算的分子力场，能够模拟有机、无机小分子以及高分子与金属等内部原子的相互作用，该力场已被证明适用于描述聚合物的摩擦学性能[26].

Fig.1 Molecules models of PTFE图1 PTFE的分子模型

模拟计算采用Forcite模块，具体操作步骤为首先对所建模型进行几何优化，精度设fine，采用Smart计算直到能量收敛精度不大于4.184×10-5kJ/mol；然后进行分子动力学退火Anneal处理，条件设置：温度为300～800 K，10次循环；选择退火后能量最低的一种PTFE构型，进行1 000 ps的NVT系综分子动力学平衡，条件设置：300 K，Nose控温；最后，对NVT得到的稳定结构进行1 000 ps的NPT系综分子动力学平衡，系统温度设置为300 K，改变系统压强设置以得到不同真空度下的模拟结果[27-28].系统压强分别为大气压(1.0×10-4GPa)、低真空(1.0×10-9GPa)和高真空(1.0×10-12GPa).最终得到PTFE模型尺寸为35 Å×35 Å×35 Å (图1)，密度分别是1.914、1.887和1.866 g/cm3，可见随着真空度的增加，PTFE的密度逐渐降低.

1.2 摩擦模型的建立与性能模拟

利用前面优化得到的PTFE模型作为中间层，以与PTFE大小尺寸相匹配的Fe原子层分别作为顶层和底层，建立1个3层的含有聚合物材料与铁的摩擦副模型，并赋予整个体系1.0×10-2GPa的正压力(图2).然后同时固定顶层和底层的铁原子，采用上述优化PTFE模型的方法对摩擦模型进行优化.优化结束后，取消对铁原子层的固定，以便对3层模型进行Confined shear.Confined shear的条件是：相对滑动速度为0.1 Å/ps，在NVT系综下运行1 000 ps，温度为300 K，系统压强设置分别为大气压(1.0×10-4GPa)、低真空 (1.0×10-9GPa)和高真空 (1.0×10-12GPa)，得到不同工况下材料摩擦磨损性能随时间变化的轨迹文件，从轨迹文件中分析提取摩擦系数、磨损性能、温度变化、相对浓度和沿厚度方向的速度变化等参数.

Fig.2 Configurations of the molecules models of pure PTFE sliding against Fe layer图2 PTFE与铁原子层的摩擦副模型

1.3 PTFE的摩擦磨损性能测试

不同真空度下PTFE的摩擦学性能试验是在中国科学院兰州化学物理研究所青岛中心空间环境模拟试验装置自带的球-盘摩擦试验机上进行，试验条件如下：摩擦对偶材料为9Cr18，直径为3.175 mm，法向载荷为1 N，温度为室温，转速设定为200 r/min，旋转直径是8.00 mm，测试压强分别为大气压(1.0×10-4GPa)、低真空 (1.0×10-9GPa)和高真空(1.0×10-12GPa).摩擦试验中磨损率的计算采用图3中公式：V代表磨损体积，r是摩擦对偶钢球半径，b是磨痕宽度，d代表旋转直径，K为磨损率，P指载荷，L代表指滑动距离.

Fig.3 Calculation for the wear rate图3 磨损率的计算公式

2 结果与讨论

2.1 摩擦磨损性能的模拟计算

为了研究PTFE的真空摩擦学性能，建立了铁原子-PTFE-铁原子3层摩擦模型，考察了这一模型在不同真空度下的摩擦系数和磨损率.通过公式μ=f/F可以求得摩擦系数，其中f代表摩擦力，F是正压力，μ是摩擦系数.不同真空度下PTFE摩擦系数随模拟时间的变化如图4所示，由图4可知，约200 ps后摩擦系数逐渐稳定，取200～1 000 ps摩擦系数的平均值，常压环境下(1.0×10-4GPa)，PTFE的平均摩擦系数为0.073，真空度为1.0×10-9GPa时，PTFE的平均摩擦系数为0.061，比常压时降低了16.4%；真空度为1.0×10-12GPa时，PTFE的平均摩擦系数为0.042，比常压时降低了42.5%.这说明随着真空度增加，PTFE的摩擦系数逐渐降低，这一结果与文献中的结果相一致[24,29].

Fig.4 The friction coefficient of PTFE with time under different vacuum degrees图4 不同真空度下PTFE的摩擦系数

为了更好地了解真空度对PTFE磨损机制的影响，提取了摩擦过程中PTFE在200、600和1 000 ps时的分子动力学摩擦快照，结果如图5所示.由图5(a～c)可以看出，初始阶段PTFE分子链在摩擦剪切作用下会发生大变形，经过继续滑动剪切，PTFE分子链变形更加严重，分子链被破坏并发生断裂[图5(d～f)]，在摩擦剪切的最后阶段[图5(g～i)]，三种工况下的PTFE分子链都发生断裂，值得注意的是在常压和低真空时模型中间出现大量断裂散落的分子链片段，而高真空时，分子链断裂后没有出现明显的分子链碎片，而主要发生的是材料向摩擦对偶的转移.这说明PTFE在常压摩擦剪切过程中容易产生磨损碎片，从而产生磨屑，而在高真空状态下，分子链断裂后，容易出现PTFE分子链向对偶面的黏着现象.

Fig.5 Molecular dynamics friction snapshot of PTFE at different time under different vacuum degree:(a～c) 200 ps; (d～f) 600 ps; (g～i) 1 000 ps图5 不同真空度下PTFE在不同时刻的分子动力学摩擦快照：(a～c) 200 ps；(d～f) 600 ps；(g～i) 1 000 ps

1973年，Fleisher提出能量磨损理论，摩擦过程中所作的功虽然大部分以摩擦热的形式散失，但是其中大约9%～16%的功以势能的形式储存在基体内部，随着摩擦过程的不断进行，当一定体积的材料积累的能量达到临界数值时，便以磨屑的形式从表面剥落，产生磨损量.聚合物分子容易黏附在对偶金属原子层表面，或者在摩擦过程中容易剪切断裂，通常，可以将离开聚合物基体的原子数除以聚合物基体总原子数求得磨损率.在本研究中提取了摩擦过程中1 000 ps时的磨损状态，如图5(g～i)所示，通过统计图中断裂原子个数可知，常压环境下PTFE的磨损率为45.2%，真空度为1.0×10-9GPa时PTFE的磨损率为54.3%；真空度为1.0×10-12GPa时PTFE的磨损率为57.6%.结果表明，随着真空度的增加，PTFE的磨损明显增加.

2.2 摩擦学机理分析

为了探讨真空度对PTFE摩擦磨损机理的影响，分别提取了摩擦模型在摩擦过程中沿厚度方向的温度和速度曲线分布图，如图6和图7所示.从图6中可以看出，对于常压下的PTFE，在沿模型厚度方向并未出现明显峰值，整个材料温度在300 K左右波动，说明材料在常压下的摩擦过程中没有明显的温升.当真空度是1.0×10-9GPa时，PTFE在沿模型厚度方向45 Å处出现了317 K的峰值，相比系统设定温度300 K，摩擦界面温度升高17 K；当真空度为1.0×10-12GPa时，PTFE在沿模型厚度方向45 Å处出现了325 K的峰值，摩擦界面温度升高25 K，这主要是由于真空环境中导热性差，使得PTFE分子与铁原子层的相互摩擦过程中产生聚集热，容易导致界面摩擦温度升高.

Fig.6 Temperature profiles of PTFE under different vacuum degrees in the thickness direction图6 不同真空度下PTFE模型内沿厚度方向温度分布

Fig.7 Velocity profiles of PTFE under different vacuum degrees in the thickness direction图7 不同真空度下PTFE模型内沿厚度方向速度分布

从图7的速度变化可以看出，PTFE在9.5 Å 处出现1个峰值，这是由于底层铁原子与聚四氟乙烯分子间的相互吸附作用造成的.在44 Å处摩擦界面，随着真空度的增加，峰值逐渐升高，而且高真空度(1.0×10-12GPa)下PTFE原子运动速度最大，这说明随着真空度的增加，摩擦界面温度升高，PTFE的分子运动速度加快，与对偶铁的相互作用变强，这与上述磨损率和界面温度增加的分析结果一致.

为了进一步探究不同真空度下材料的摩擦磨损机理，分别提取了材料在摩擦过程中沿厚度方向的原子相对浓度分布曲线，如图8所示.由图8可知，边界效应导致PTFE材料在下层接触界面和上层摩擦界面均出现相对原子浓度的峰值，随着真空度的升高，PTFE在界面处的相对原子浓度逐渐升高，说明在摩擦界面处PTFE分子链与对偶铁存在较强的相互作用，大量的PTFE分子吸附在对偶铁表面，这也是造成黏着磨损的主要原因.

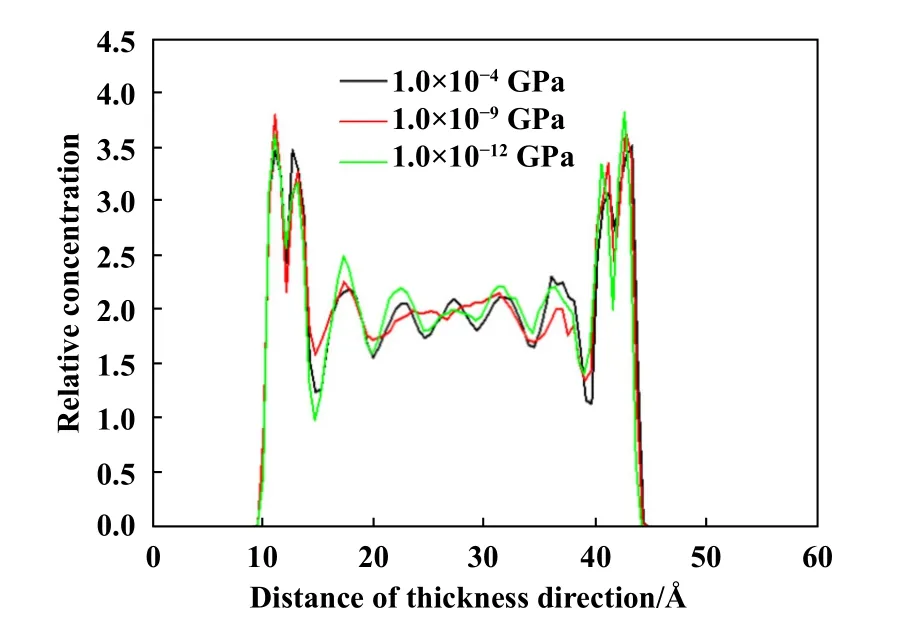
Fig.8 Relative concentration profiles of PTFE under different vacuum degrees composite in the thickness direction图8 不同真空度下PTFE模型内沿厚度方向原子相对浓度

为了进一步分析材料与对偶铁之间的相互作用强弱，提取了铁原子与氟原子之间的径向分布函数，如图9所示.从图9中作用曲线可以看出，随着X方向上滑动距离的逐渐增大，径向分布函数(RDF)值呈现出逐渐增加的趋势，这说明由于范德华力、静电吸附和其他相互作用力，在一定载荷条件下，在摩擦过程中更多的聚四氟乙烯分子与对偶铁原子发生相互作用.而且，随着真空度的升高，RDF的平均值越高，说明真空度增加，在滑动过程中更多的PTFE分子向对偶铁原子移动.

Fig.9 RDF values of Fe atoms and F atoms of PTFE during the process of wear图9 PTFE模型内氟原子与铁原子径向分布函数

2.3 摩擦磨损性能的试验验证

图10所示为不同真空度下PTFE摩擦系数随时间的变化曲线和磨损率.随着摩擦时间延长，PTFE的摩擦系数逐渐增大，在600 s时，摩擦系数趋于稳定.比较600～1 800 s的摩擦系数的平均值，常压环境下(1.0×10-4GPa) PTFE的平均摩擦系数为0.17，真空度为 1.0×10-9GPa时PTFE的平均摩擦系数为0.158，比常压时降低了7.1%；真空度为 1.0×10-12GPa时PTFE的平均摩擦系数为0.139，比常压时降低了18.2%.说明随着真空度增加，PTFE的平均摩擦系数逐渐降低.真空度为1.0×10-9GPa时，PTFE的磨损率为 16.8×10-3mm3/(N·m)；真空度为1.0×10-9GPa时，PTFE磨损率为 15.5×10-3mm3/(N·m)；真空度为1.0×10-12GPa时，PTFE的磨损率为11.5×10-3mm3/(N·m).由此可以得到结论，真空度增加，PTFE的磨损率升高.这一结果验证了前面的分子动力学计算的结果.

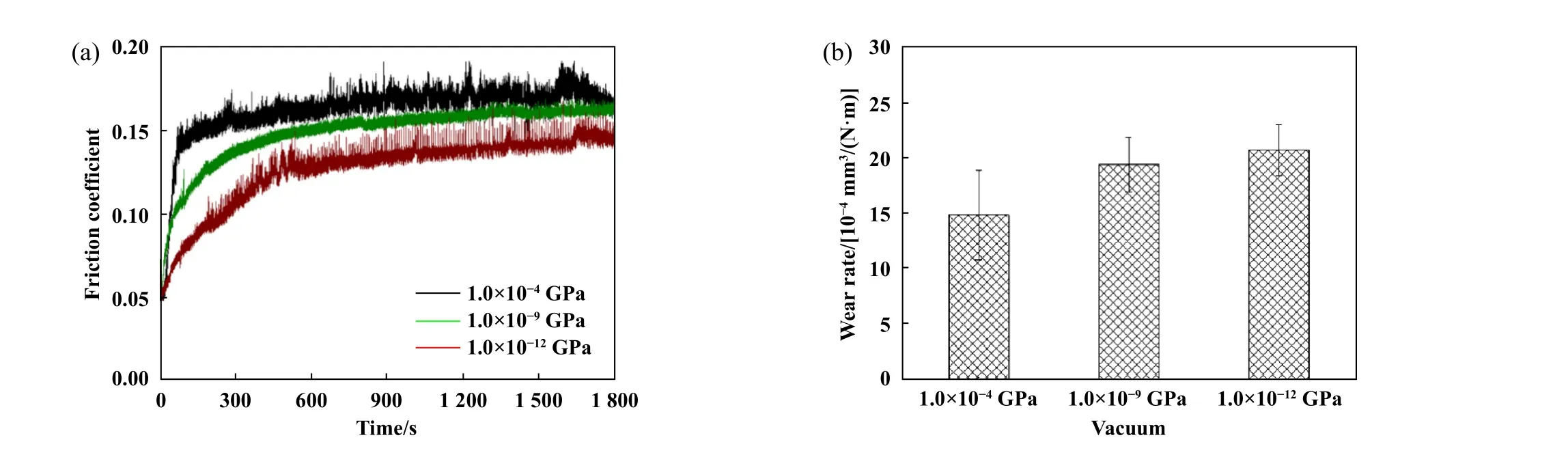
Fig.10 (a) The friction coefficient and (b) wear rate of PTFE under different vacuum degrees图10 不同真空度下PTFE摩擦性能表征：(a)摩擦系数；(b)磨损率

3 结论

在本研究中，利用分子动力学模拟来研究聚四氟乙烯在不同真空度下的摩擦磨损行为，从原子水平探索聚合物与金属铁原子的内在作用机理，主要结论如下：

a.利用分子动力学模拟发现，常压环境下PTFE的平均摩擦系数为0.073，随着真空度的增加，摩擦系数逐渐降低，当真空度为1.0×10-12GPa时，PTFE的平均摩擦系数为0.042，降低了42.5%.

b.摩擦剪切的初始阶段PTFE分子链会发生大变形，随着时间的延长，PTFE出现了分子链的断裂破环，从而造成分子链的断裂，产生材料的磨损.在大气压时摩擦剪切过程中容易产生磨损碎片，高真空状态下，容易发生PTFE分子链向对偶面的黏着.随着真空度的增加，PTFE的磨损明显增加.

c.从摩擦界面微观分析发现，真空度升高，更多的PTFE分子链与对偶铁原子进行摩擦作用，摩擦界面温度升高，原子受到温度的影响，运动速度加快，在滑动过程中更多的PTFE分子向对偶铁原子移动，导致磨损量变大.

d.不同真空度下PTFE的摩擦试验结果表明，随着真空度的增加，PTFE的摩擦系数逐渐降低，磨损率变大，试验结果与理论计算结果相一致.