密里根油滴实验的理论分析和测量结果讨论
陈学文,张家伟,方 旺,向思璇,谢腾辉,张欣笛
(重庆科技学院 数理与大数据学院,重庆 401331)
1 关于密立根油滴实验
电荷不连续性的发现和电子电量的精确测定推进了人们对微观结构的认识。密立根油滴实验是由实验物理学家密立根首先设计并完成的,在近代物理学的发展史上是一个十分重要的实验。它证明了任何带电体所带的电荷都是某一最小电荷——基本电荷的整数倍;明确了电荷的不连续性;并精确地测定了基本电荷的数值,为实验上测定其他一些基本物理量提供了可能性[1]。密立根从1906年开始致力于微小油滴带电量的测量,用了11年时间,经过多次重大改进,终于以上千颗油滴的确凿实验数据无可辩驳地证实了电荷的量子性,并测出基本电荷的电量e=(1.5924±0.0017)×10-19C,现代精确值为1.602×10-19C。而在当前实验条件远比密立根时期好的情况下,当代大学生能否“重复密立根的故事”?这是一个值得思考的问题。
密立根油滴实验是理工科大学物理实验中一个十分重要的近代物理实验,目前已有很多文献从不同方面对该实验作了分析讨论。文献[2]分析了密立根油滴实验测量结果的不确定度;文献[3]讨论了基于大数据分析思路的油滴实验数据处理方法;文献[4]—[5]分别借助Origin软件和Mathematica软件讨论了密立根油滴实验的数据处理;文献[6]—[8]讨论了密立根油滴实验中油滴的选取原则等。由于大学物理实验课时的限制,在实际测量时一般要求学生选择5颗不同的油滴进行测量,或者只选择1颗“合适”的油滴,对该油滴测量5次平衡电压和下落时间。针对测量得到的油滴带电量,采用“倒过来验证法”来确定该油滴所带基本电荷的“量子数”,进而计算基本电荷量。
密立根油滴实验是测量微小油滴的带电量,而不是电子的电荷。该实验通过对宏观量的观测来揭示微观量本身所具有的属性,所以必定要通过对大量观测数据的计算和统计。只有测量足够多数量的油滴,找出油滴带电量分布,才能深刻体会电荷量子化的内涵。在“大学物理实验”课堂实际测量过程中,学生往往有以下三个困惑:①为何要求平衡电压介于150 V到400 V之间,下落时间控制在15 s到30 s之间?②“静态平衡法”测量过程中为何可将油滴看作“匀速下落”?③如何通过1颗或5颗油滴的带电量得出“电荷量子化”的结论?
本文针对学生在做密立根油滴实验中存在的三个主要困惑,首先结合油滴带电量、平衡电压和下落时间三者之间的关系,从理论上分析选择合适平衡电压和下落时间的原因;进而从力学角度分析在测量过程中油滴“匀速”下落的合理性;最后基于312颗油滴的测量数据,按照油滴的带电量进行分类,发现当电荷量不超过5 e时,可明显看出电荷分布的量子化,但当电荷量大于5 e时,量子化现象不明显。
2 油滴电量、平衡电压和下落时间之间的关系
在实验中,经雾化后的油滴的大小和电荷具有随机性,必须选择平衡电压和匀速下落时间合适的油滴,才能满足验证物体带电量不连续和提高实验结果精确度的要求。本文首先通过不同带电量油滴下落的U-tf关系讨论如何选择合适的油滴。在平衡法中,油滴所带的电量由下式给出[9]:


表1 实验所用的参数值
将各物理量的具体数值代入r0的表达式和式(1)可得:

若已知油滴的电荷量q,由式(3)可得平衡电压和下落时间的关系满足:
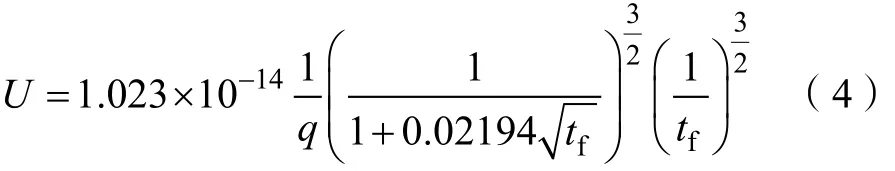
图1基于式(4)给出了油滴取不同电荷量时,平衡电压与下落时间的关系。从图1可以看出,当平衡电压取150~400 V,下落时间取16 s以上时,油滴的带电量理论上不超过 5 e;若将平衡电压控制在200~400 V,下落时间在20 s以上时,油滴的带电量理论上不超过3 e。结合式(2)和图1还可以看出,当油滴下落s(s=1.6 mm)距离所用时间tf<16 s时,油滴半径大于0.93μm,油滴质量较大,在相同平衡电压情况下,携带的电量必然也大;当tf>45s时,油滴半径小于0.55μm,此范围内的油滴将受到较强的布朗运动的影响[10]。因而实验时一般要求平衡电压取150~400 V,下落时间约为20 s[9]。在实际测量中,选择平衡电压 U ∈ [1 50,400](V)、下落时间 tf∈[20,30](s)的油滴进行测量,所测油滴带电量大多为2 e或3 e,此情况下的测量结果最为理想。文献[11]从不确定度的角度分析了油滴的选取范围:对于平衡法,若所选油滴的平衡电压范围取下落时间则电荷不确定度

图1 不同电量下密立根油滴下落时间与平衡电压的关系
3 油滴下落的动力学分析
从喷油嘴喷发出来的油滴在摩擦力的作用下,带大小不等、正负随机的电荷。根据实验仪器给出的相关参数,带电油滴半径一般在微米量级。为了从理论上计算油滴的运动速度,本文把小油滴近似看成小球,把空气近似看作流体,在没有外加电场的条件下,油滴下落过程中受到重力与空气粘滞阻力的共同作用,并在一段时间之后达到匀速(见图2)。

图2 油滴受力情况示意图
实验中,首先通过预设一个平衡电压U来筛选合适的油滴。加上预设的平衡电压后,油滴若在重力、浮力和电场力的作用下受力平衡,则在两带电平板之间静止(如图2中O点)。待油滴平衡后,将仪器从“平衡”调至“工作”状态,此时电压增加到200 V,油滴加速上升并迅速达到某一匀速v0。油滴上升到P点后,再将仪器从“工作”调至“平衡”状态,此时油滴“相当于”只受空气粘滞阻力的作用。油滴所受的粘滞阻力为[12-13]:

式中,ρ为空气密度;s为油滴截面积;C为阻力系数,与空气(流体)的雷诺数Re有关。R是一种用来表征流体流动情况的无量纲数,其中η为流体的粘滞系数,D为球形油滴的直径。C与Re的关系可近似为:

实验中油滴速度v很小, Re≪ 1 ,式(6)中第二、三项可忽略,代入式(5)后得到:



当油滴的速度达到0.9999vm时(vm为油滴下落的极限速度),认为油滴运动为匀速运动,从式(9)可得到油滴从静止加速到0.9999vm所需的时间为t = 9.21s gtf。表2给出了tf取不同值时油滴达到匀速所需的时间及下落的距离。从表2可以看出,油滴在极短时间内就近似达到了极限速度,因此对于匀速区域的选取并不需要特别说明,实验本身的设计是十分合理的。

表2 不同下落时间情况下油滴达到匀速的运动距离l
4 实验测量结果分析
密立根油滴实验需要通过对大量观测数据的计算和统计,找出油滴带电量分布,才能“看到”油滴电荷分布的“量子化”现象,才能深刻体会电荷量子化的内涵。为此,本文基于312颗油滴的测量结果,给出了这312颗油滴带电量随平衡电压和下落时间的分布(见图 3)和不同油滴所对应的平衡电压和下落时间的关系(见图4)。可以看出,在误差范围内油滴电荷分布为基本电荷量(191.6× 10 C)的整数倍,这充分说明油滴电荷确实是“量子化”的。
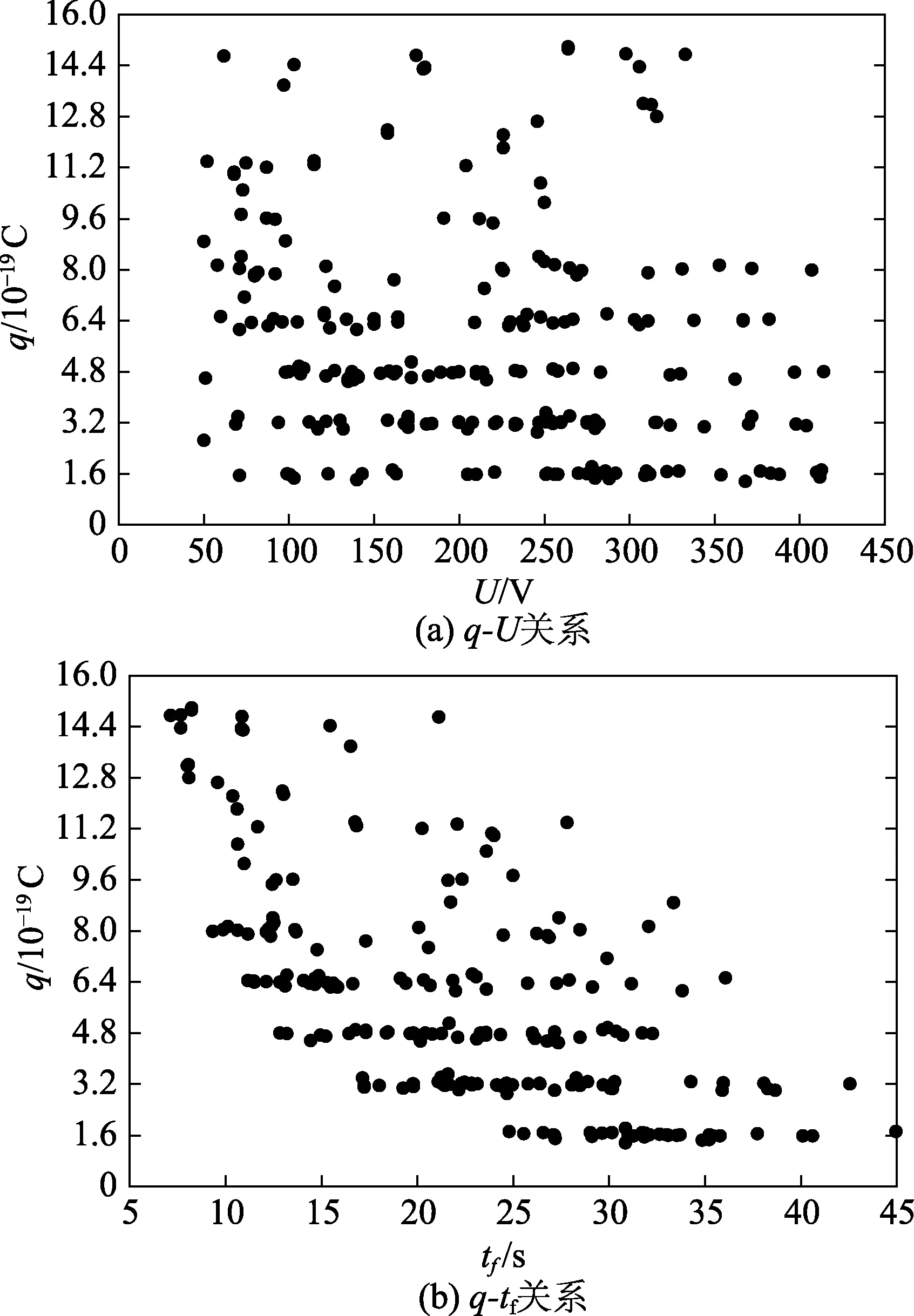
图3 不同平衡电压和下落时间时的油滴电量分布

图4 不同油滴所对应平衡电压和下落时间的关系
从图3可以看出,当油滴带电量q≤5e时,电荷的“量子化”现象明显,而当q>5 e时,电荷的“量子化”现象不明显;当平衡电压U< 1 00 V 时,所得到的油滴带电量大多分布在q≥4 e区间;当下落时间小于10 s时,所得到的油滴带电量大多分布在q≥5e区间。从图4可以看出,若油滴带电量q=e,相对误差偏大;若油滴带电量为2~4 e,实验得到的数据基本上和理论值在同一条曲线上;若带电量在5 e及以上时,相邻电荷之间的油滴带电量偏离“电荷量子化”,没有明显的“分界”。
5 结语
本文从静态平衡法完成密里根油滴实验的原理出发,首先从实验的理论分析着手,分析了不同半径和带电量的油滴与平衡电压和下落时间的关系,解释了选取合适油滴的原因;进而从力学角度推导了油滴下落过程中速度与时间的关系,发现油滴只需经过约0.1 ms或更短时间便可达到匀速,远低于人的反应时间,因而实验设计是合理的;最后基于大数据的实验测量结果,直观显示了油滴电荷分布在误差范围内为基本电荷量的整数倍,证实了电荷的量子性。
通过本实验,学生最重要的收获是通过测量密立根油滴电荷量来深刻体会电荷量子化。在“大学物理实验”课堂中,若能清楚阐述本文的内容,学生则能深刻理解密里根油滴实验的精妙之处,深刻理解实验的精髓,而不是仅仅为了测量而测量。

