能耗最优下轮式移动机器人作业路径规划的最优节点A＊算法

江磊，贾文友，刘莉，梁利东，魏文涛

（安徽工程大学 机械工程学院，安徽芜湖 241000）

随着科技的发展，机器人的应用也越来越普遍，其中，轮式机器人[1-3]是目前科学技术发展最活跃的领域之一[4]，国内关于轮式移动机器人路径规划方法的文献目前仍处于增长的状态[5]。任建华等分别从传统路径规划和现代路径规划两个方面对路径规划方法展开了研究，以A*算法和蚁群算法为例进行了仿真实验[6]；关泉珍等提出采用高精度地图构建技术还原路况信息，结合A*算法，在标记为有障碍的栅格模型中，为机器人寻找一条恰当的从起始点到目标点的运动路径[7]，但是从仿真结果看出，该路径可进行进一步的优化；康靖等提出了一种改进的蚁群算法，为轮式机器人在复杂地形中探索并规划出一条最省能量的行走路线[8]；刘贵杰等通过建立AUV 运动的速度模型和能耗模型获得AUV 规划路径的总能耗，并采用蚁群算法，对降低水下机器人能耗、提高续航能力有一定的优势[9]；张浩杰等兼顾考虑机器人对降低能耗和路径规划效率两方面的需求，提出了一种基于改进AD*算法的移动机器人低能耗最优路径规划方法[10]；Zhang 等针对差分转向，阿克曼转向，滑移转向和全向转向轮式机器人的节能运动规划问题进行了综述研究[11]；Krimsky 等介绍了能量回收执行器，使用一系列弹簧和离合器来捕获并带回与电动机并联的弹性势能，以达到减少能量消耗的目的，然而仅在特定的情况下才可节能[12]；Datouo 等将新的代价函数和启发式函数集成到传统的A*算法中，考虑了地面摩擦、转弯、速度及功率造成的能耗，但是并未考虑到势能变化造成的能耗[13]；Mauricio 等提出了一种两轮差速驱动移动机器人的功率模型，考虑了机器人及其电机的动力学参数，预测了不同加速度和不同有效载荷下的运动轨迹的能量消耗[14]。综上，基于电机效率、地面摩擦、地面起伏、速度变化、转弯等多因素，构建能耗模型，利用改变搜索方式，提出能耗最优下轮式移动机器人避障路径规划的最优节点A*算法（简称ONA*），实现轮式移动机器人在单位能耗最优约束下以更少的时间规划出理想作业路径。

1 A＊算法简介

A*算法是一种静态路网中求解最短路径最有效的直接搜索方法，是一种典型的启发式搜索算法，其对每一个搜索的节点进行评估，得到最好的节点，再从这个节点进行搜索，直至搜索到目标。对于评估节点n的估价函数f（n）为

式中：f（n）为从起始节点到n节点的实际代价；g（n）为从n节点到目标节点的预估代价。

A*算法在搜索过程中，拥有open 表和close 表，其中open 表中存储待被搜索的节点，close 表中存储已被搜索过的节点。g（n）表示搜索的广度的优先趋势，计算当前点周围相邻的各个n节点（共8 个）的实际代价，在每次计算之后记录n节点的父节点；h（n）是在对一个节点估价时的约束条件，如果约束条件越多，则排除的节点越多，估价函数越好，如果h（n）精确地等于从n移动到目标的代价，则A*将会仅仅寻找最佳路径而不扩展别的任何节点，则运行最快；f（n）表示评估节点n的重要程度，在open 表中所有已评估过的节点中，最优的节点将被下次搜索选中作为当前点，然后从当前点继续搜索，直至目标节点。在搜索到目标点后，回溯查找其父节点、父节点的父节点，直至起点，即为最优路线。

2 轮式移动机器人能耗模型构建

轮式移动机器人在作业过程中，能耗受约于多因素，主要包括电机效率损失的能量（记为Ep）、地面起伏时的势能（记为Eh）、滚动摩擦阻力消耗的能量（记为Ef）、速度变化和转弯消耗的能量（记为Ek）等方面。本文采用两轮驱动轮式机器人，图1 是机器人匀速转弯时的示意图。

图1 轮式机器人转弯示意图

式中：r为机器人驱动轮半径；B为机器人左右两侧轮距。

2.1 电机效率损失的能量

电机对外做功时，会有转化效率问题，其对外输出并不能百分百转化出去，效率而损失的能量，计算公式为

式中：η为电机效率；P为电机功率；Scn为从n节点的父节点到n节点之间的路程；vn为机器人在n节点平移的速度；vn−1为机器人在n节点的父节点平移的速度。

2.2 地面起伏时的势能

轮式移动机器人运动时，地面是非平整的，会有爬坡和下坡。下坡时，小型电机不能很好的将能量回收，而是以热量的形式耗散掉，故不考虑下坡时的能量回收。爬坡时，能耗为

式中：m为轮式移动机器人的质量；g为重力加速度；Δh为当前点到下个点的高度差。

2.3 滚动摩擦阻力消耗的能量

轮式机器人在向目标移动时，克服轮胎与地面的摩擦阻力需要消耗能量，则

式中：μ为滚动摩擦因数；θ为坡道与水平面之间的夹角。

2.4 速度变化和转弯消耗的能量

加速时，需要电机对外做功；减速时，能量转化为热能消耗掉，转弯同样要消耗能量，计算公式为

式中：I为转动惯量；ω为机器人转弯时的角速度。

根据式（3）～ 式（6），轮式移动机器人在运动过程中的总能耗记为E，构建能耗模型为

3 轮式移动机器人能耗最优约束下A＊算法的改进

3.1 节点的估价函数推导

基于A*算法的能耗最优路径规划的路径搜索过程中，节点的评估函数f（n）是关键。根据轮式移动机器人在运动过程中的总能耗式（6），其为节点的实际代价，即

对于n(x1,y1,z1)节点和目标节点ngoal(x2,y2,z2)，两者之间的预估距离采用对角线距离，即S（n），则：

式中Sdiagnol（n）和Sstraight（n）分别表示沿着对角线移动的距离和曼哈顿距离；非爬山路况中，因路线往竖直方向变动的趋势很小甚至没有，故Sdiagnol（n）和Sstraight（n）不计入竖直方向上的差，式（9）和（10）分别简化为：

则采用A*算法时，在能耗最优路径规划下的预估代价h（n）为

综上，能耗最优下轮式移动机器人路径规划的最优节点 A*算法，由式（1）得能耗最优策略下节点的估价函数f（n）为

3.2 能耗最优下轮式移动机器人作业路径规划的最优节点A＊算法（ONA＊）

在搜索过程中，当前节点放入close 表中，并把当前节点的8 个邻节点中未被放入open 表中可通行的节点放入open 表中；在下次循环中，再在open 表中搜索到f（n）值最小的节点作为当前节点，再从该节点进行搜索。当轮式机器人作业的地图较大，从搜索过程需要花费较长时间。

为此，提出一种新的搜索最优点方式，在把当前节点的8 个邻节点中未被放入open 表中的可通行节点放入open 表后，再将其放入每次寻找新的当前节点后都会被清空的cacu 表中，同时把已在open 表中，但g（n）值更低的节点也放入cacu 表中，再从cacu 表中找到f（n）值最小的节点作为预选节点np。判断该预选节点是否在障碍范围内，若在，则找出障碍范围内f（n）值最小的节点与np的f（n）值相比，较小者作为当前节点；若不在，预选节点np直接作为当前节点，从而避免局部最优的情况出现。若cacu 表为空，再在open 表中找f值最小的节点作为当前节点。在此情形下，大多数是最多会从8 个点中找到最优节点，而不是从open 表中找到最优节点，从而提高算法的运行速度。

综上，ONA*算法流程图如图2 所示。

图2 ONA*算法流程图

步骤1 如果是首次循环，则起点作为当前节点n，跳转至步骤五，否则继续往下执行。

步骤2 如果cacu 表是空表，从open 表找到离目标点最近的f（n）值最小的节点作为当前节点n，跳转至步骤5，否则继续往下执行。

步骤3 找到cacu 表中f（n）值最小的节点，将该最小节点作为预选节点np。

步骤4 判断预选节点np是否在障碍范围内，若在，找出障碍范围内f（n）值最小的节点n' p，与np的f（n）值比较，若小于np的f值，将n' p作为当前节点n，否则将np作为当前节点n；若不在，则np作为当前节点n。

步骤5 将当前节点n放 入close 表中，之后的循环中，该节点将不会再被当作当前节点。

步骤6 设置空表cacu 表。

步骤7 若当前节点n是目标节点（则寻路成功）或open 表已为空表（则寻路失败），算法结束，否则继续往下执行。

步骤8 搜寻点n的8 个邻节点，如有不可越过的节点，放入close 表中。

步骤9 如果某邻节点，既没有在open 表，也不在close 表中，将其放入open 表，计算出该邻节点的f（n）值，并设父节点为n。如果已在open 表中，判断其g（n）值是否更小，若是，则用更小的g（n）值替换原来的g（n）值，同时在预估代价值h（n）前引入比例因子α，重新计算f（n）值，并设父节点为n，否则查看其它邻节点，将f（n）值更新的邻节点放入cacu 表中。

步骤10 所有邻节点查看完毕后，跳回步骤2。

4 仿真实验验证及应用案例

4.1 轮式移动机器人相关参数确定及作业环境地图搭建

为了验证上述提出ONA*算法的有效性，采用MATLAB R2016a 进行寻路的仿真验证，仿真所用计算机为Lenovo R7000，CPU 型号为AMD Ryzen 7 4800 H with Radon Graphics，主频为2.90 GHz。轮式移动机器人的相关参数如表1 所示,仿真实验关键参数如表2 所示，其余未给出具体数值的参数，在移动机器人移动过程中会有变化，需由已给出的参数实时计算。

表1 轮式移动机器人相关参数

表2 仿真实验关键参数

当再次计算某个节点时，预估代价值h（n）前引入比例因子α确定，经实验验证，取值α 较小时，仿真速度慢；α较大时，仿真误差大。本验证实验取α=10。

轮式移动机器人在平地上时，单个轮子所受到的转矩为

轮式移动机器人在爬坡时，单个轮子所受到的转矩为

由式（16）和式（17）可推出轮式移动机器人在平地上和在爬坡时的功率关系为

在转向时，电机需要消耗额外的功率，参考康亚彪[15]对野外无人车转向的研究，转向时机器人单个轮子的功率表示为

轮式移动机器人作业环境地图平面尺寸为192 × 192，具有凹凸不平整特性，不可越过的区域设为红色；设置起点坐标为（3，3，0.2），终点坐标为（183，168，0.2），MATLAB 生成的具体地图如图3 所示。

图3 尺寸为192 × 192 的轮式移动机器人作业环境地图

4.2 ONA＊算法实验结果分析

ONA*算法以能耗最优为目标，距离是其中一项重要参数，为此对比能耗最优约束下A*算法（A*algorithm with optimal energy，OEA*）和距离成本最优约束下A*算法（A* algorithm with optimal distance，ODA*），采用相同的轮式移动机器人的相关参数和仿真实验参数在MATLAB 中进行规划寻路，仿真结果分别如图4～图6 所示。

图4 ONA*算法下轮式移动机器人作业规划寻路仿真结果

根据图4～图6 的仿真结果，从路径长度、能量消耗、单位距离能耗和算法寻路时间等进行对比分析，具体结果如表3 所示。

表3 三者的实验结果对比

对比ONA*算法和OEA*算法，由图4、图5 和表3 可知，ONA*算法和OEA*算法所寻路径长度基本一致，但ONA*算法所寻路径转弯次数有所减少，且单位距离能耗降低了近6.4%，算法寻路时间降低了86.9%；对比ONA*算法和ODA*算法，由图5、图6 和表3 可知，ONA*算法能避开ODA*算法不必要的爬坡，ONA*算法中单位距离能耗降低了17.5%，寻路时间也降低了30.4%。可见，ONA*算法具有良好综合效果。

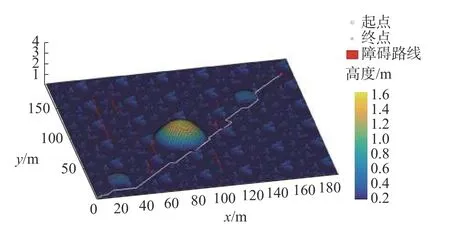
图5 OEA*算法下轮式移动机器人作业规划寻路仿真结果

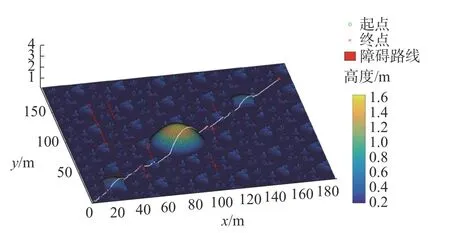
图6 ODA*算法下轮式移动机器人作业规划寻路仿真

4.3 ONA＊算法应用案例

ONA*算法既能够适应于不同广域的作业环境地图案例，平面尺寸可从32 × 32 小地图（如图7 所示）到192 × 192 大地图（如图8 和图9 所示）；又能机器人从作业环境地图不同方向进行作业寻路案例，可从作业环境地图的ONA*算法下轮式移动机器人在小地图中作业避障寻路应用寻路（如图7 所示）或从作业环境地图的左下角到右上角寻路（如图8 和图9 所示）。

图7 ONA*算法下轮式移动机器人在小地图中作业避障寻路应用

图8 ONA*算法下轮式移动机器人起点在左上角的大地图中作业避障寻路应用

图9 ONA*算法下轮式移动机器人起点在右上角的大地图中作业避障寻路应用

由图7～图9 可得出，ONA*算法在寻路过程中，能够在多种避开不必要的爬坡同时，选择一条理想的路，进一步验证了ONA*算法有效性。

5 结论

因轮式移动机器人每次作业携带的能源有限，提出了能耗最优下轮式移动机器人避障路径规划的最优节点A*算法（ONA*），通过与能耗最优约束下OEA*算法和距离成本最约束下ODA*实验验证对比，ONA*算法不论在单位距离能耗，还是在算法作业规划寻路时间，都有较大缩短，综合效果好；ONA*算法适用案例既不受约于作业环境地图规模大小、障碍密集程度，又不受约于机器人作业方向，能为轮式移动机器人规划出一条单位距离能耗优的理想作业路径。