折叠突变的列车脱轨理论研究与仿真

刘雨梦，刘学文，张文静

（上海工程技术大学 机械与汽车工程学院，上海 201620）

随着道路交通的快速发展，列车逐渐成为人们频繁使用的交通工具，从最初的火车到现在的高铁，列车速度提升的同时，其运行安全性也被大家重视起来。近些年来，列车脱轨事故时有发生，对人们的生命安全和财产安全造成了极大的威胁，许多专家学者[1-2]对事故分析研究，针对事件制定防范措施，避免类似事故再次发生。

最早研究列车脱轨理论的是法国工程师Nadal，他提出了著名的Nadal 理论[3]，即用轮轨处于点接触时车轮开始悬浮时的脱轨系数，作为判定脱轨的标准。国内外对此理论均表示赞同，并应用此理论进一步研究列车脱轨，取得了一系列成果。韩梅等[4]推导出横向力作用下脱轨系数的计算公式，分析列车在不同工况下的脱轨系数与重车重心高度的关系。冯陈程等[5]研究货物重心横向偏移对于列车通过曲线时影响，根据脱轨系数和轮重减载率可以判断重心横向偏移量越大，车辆越容易发生危险。Koo 和Cho[6]通过在没有轮轨接触的情况下应用脱轨系数理论等，预测在该虚拟测试模型的脱轨；Wu 等[7]描述了脱轨系数，运动稳定性理论和能量随机分析理论，总结了列车脱轨的主要原因及相应的预防措施。Chen 等[8]考虑了线性和非线性蠕变力和各轮对和转向架的横向位移、垂直位移、横摆角和偏航角。得出：随着悬挂参数的增大，转向架系统的脱轨系数普遍降低；Ling 等[9]建立了高速列车与轨道耦合的动态脱轨分析的三维动力学模型，研究了高速列车通过带扣轨道时的动态脱轨响应。唐语等[10]针对中低速悬浮道岔，建立数学模型，运用联合仿真分析，为高速悬浮列车设计提供基础。

车辆脱轨是一个复杂的动力学过程，影响因素很多，很难从理论上详细描述脱机理。列车的在轨安全运行到完全脱轨可以看作是一个状态突变的过程，因此可以采用突变理论研究脱轨。李竹文和戴焕云[11]考虑脱轨系数和冲角两个因素，建立列车脱轨尖点突变模型，仿真得出：减小冲角，可以减少危险区域，有利于防止列车脱轨；刘文辉和戴焕云[12]运用初等突变里的燕尾突变，主要考虑脱轨系数、冲角和脱轨系数超限时间对列车脱轨的影响，建立突变模型。并利用Simpack 仿真得出：当以上3 个因素同时满足条件时，车辆就会发生脱轨；Wang 等[13]采用尖点突变模型，描述了运行阶段轨道交通系统安全动态变化过程的规律。利用该模型，构建了铁路系统风险分析框架，并对铁路系统安全风险领域提出了一些设想。

然而现有的运用突变理论研究列车脱轨都是直接使用突变模型的势函数方程，并没有指出这个突变势函数的数学推导过程，以及该势函数可以用来评判列车脱轨的原因。因此，本文将折叠突变理论应用于列车脱轨研究，运用数学的方法，根据列车临近脱轨时的受力分析，推导出折叠突变的势函数方程，进而研究列车脱轨。

1 突变理论

突变理论起源于光滑映射的奇异性理论和动力学系统的分叉理论。其核心内容是用来说明系统对于光滑变化的外部条件的突如其来的反应，而产生的突发变化[14]。

突变理论的数学渊源可以追溯到Poincare[15]，他指出常微分方程的解有3 个要素：结构稳定性、动态稳定性和临界集。1930 年出现的Morse 引理，对于突变理论的数学基础是一个重要贡献。突变理论的创始人Thom 在19 世纪50 年代引入横截性概念，之后又用这个概念对梯度系统的奇点进行分类，提出了分类定理，在控制变量不大于5 个时，对结构的初等突变进行分类。本文所涉及到的突变模型势函数为

式中：x为状态变量；u为控制变量。

平衡曲面（突变流形）M 表达式为

2 列车脱轨突变模型建立

在众多的列车脱轨事故中，其中有的列车经过长时间运行均未脱轨，而恰好在某处线路处脱轨，则可能该处线路有问题；但是该处线路通过了许多列车均未发生脱轨事故，唯独该趟列车脱轨，又可能说明该趟列车有问题。所以事实表明，列车脱轨事故的产生是各种不利因素综合作用的结果。

为此，本文研究的是列车在直线上运行发生脱轨，从脱轨关系角度分析来看，直线区段列车发生脱轨时,主要是存在爬轨现象。虽然列车在直线上脱轨发生的概率很小，但是风力过大、货物偏心装载、货物超限装载、货物装载加固不良等引起列车横向中心偏移，也是可能引起列车在直线上脱轨。

2.1 折叠突变模型势函数建立

本文主要考虑列车在直线运行时受到横向振动加速度的影响，因此采用折叠突变模型分析列车运行状态。对直线上列车临近脱轨时受力分析，建立列车脱轨事故的势函数方程。

当列车在直线运行发生脱轨现象，主要受车体横向振动加速度影响，车辆在直线上受到重力、风力、横向惯性力、轨道垂向支反力和横向支反力共同的作用。当风力以及列车重心偏转角过大时，在横向振动加速度的作用下，列车有可能脱离轨道，发生严重的事故，造成人力与物力的严重损失。列车发生事故时的受力分析如图1 所示。

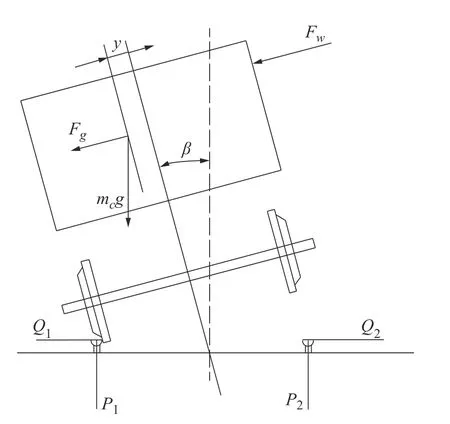
图1 列车脱轨时受力分析

本文在静力学建模中，忽略次要因素的影响，作如下假设：

1）忽略车体重心垂向位置的变化；

2）忽略车辆的垂向惯性力；

3）忽略簧下质量；

4）忽略簧下质量的横向惯性力；

5）忽略簧下部分所受的风力。

图1 中：β为重心偏转角，当 β超过一定数值时，列车脱轨。由图1 受力分析可得列车脱轨时所受的沿车体水平方向的力之和为

根据势能原理和力矩平衡可得到：

对式（5）进行变换可得

其中，当 β较小时，sinβ ≈tanβ ≈β，整理式（7）得到列车脱轨时的势函数表达式为

对势函数求导，得突变流形，其平衡曲面M 表达式为

对平衡曲面M 方程求导得非孤立奇点集为

联立式（9）和式（10）可得：

消去β 得到分叉集，表达式为：

2.2 实际列车模型

2.2.1 实际列车模型参数选择

选择 C64k 型敞车（转 K2 型转向架）为研究对象，其计算参数如表1 所示。

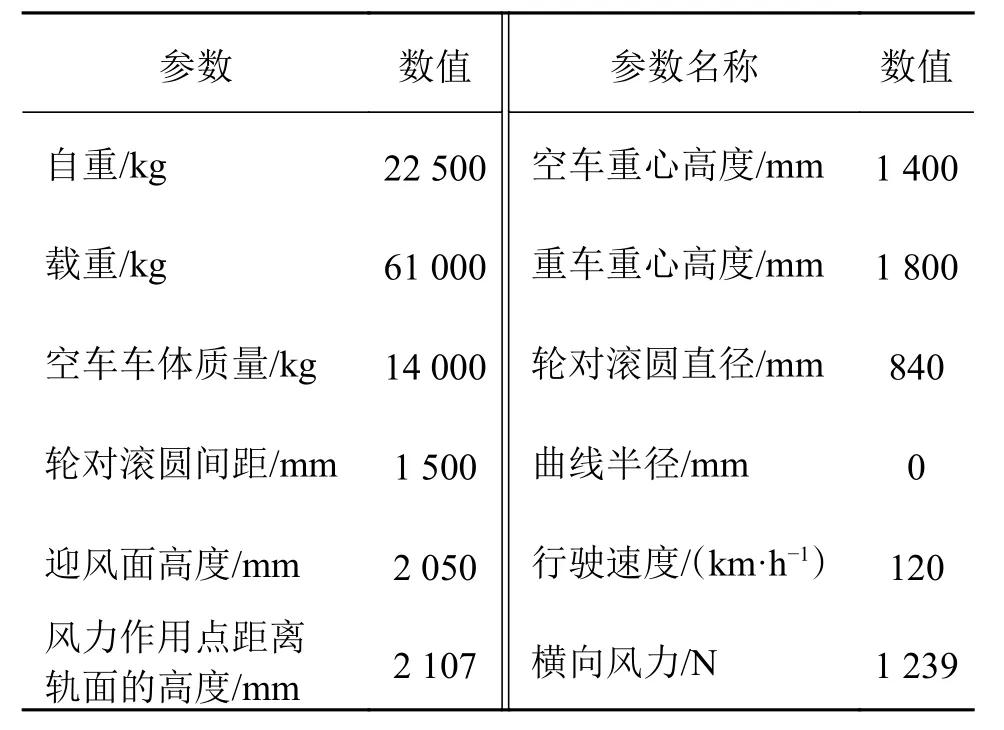
表1 C64k 型敞车计算参数

由于列车直线运动，内外轮轨道的横向支反力，因此代入势函数方程得P1=P2

2.2.2 折叠突变模型应用与分析

由此可画出列车脱轨时的折叠突变模型如图2所示。

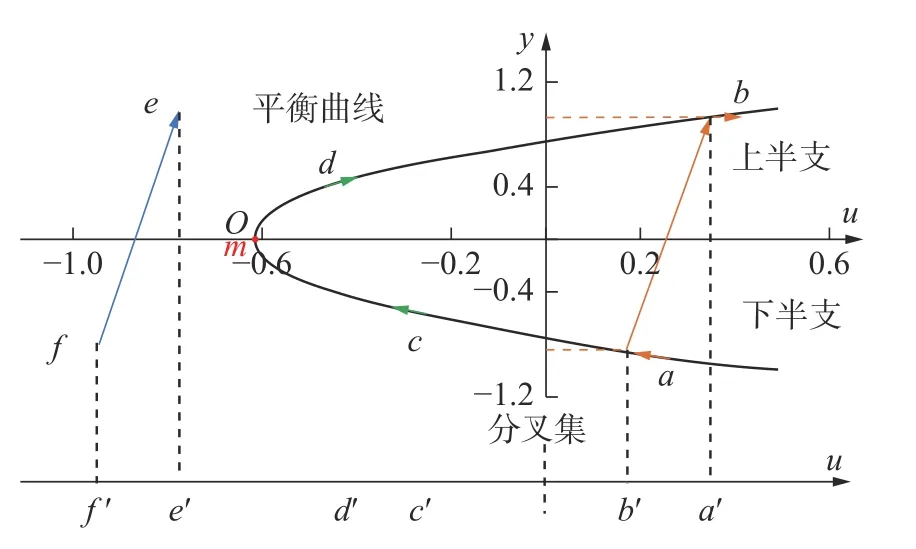
图2 不同路径分析示意图

由图2 可知：控制空间由分叉集分为两个区域，当系统处于左侧区域时，u＜m，平衡方程无实数解，折叠突变势函数无实数解，无论a如何改变，系统始终保持稳定；当系统处于右侧区域时，u＞m，方程存在两个实数解，即存在一个稳定平衡点一个不稳定平衡点，所以该区域为不稳定区域。

按不同路径分析：

路径f→e，系统处于稳定区域，不会发生失稳；

路径c→d，系统处于不稳定区域，平衡点由下半支的稳定区域经过O点，上升到上半支的非稳定区域，该过程系统一直处于渐进变化，未发生突变；

路径a→b，整个系统处于非稳定区域，且平衡点从稳定的下半支跃升到非稳定的上半支，系统产生突变。

3 仿真分析

3.1 车辆-轨道耦合模型的建立

通过上述可知，本文基于初等突变理论建立了折叠突变模型，并根据分叉集给出了列车在直线区段由于路面不平顺而引起的列车运行不稳定。现选用C64k 车辆的各项基本参数，其中包括车体质量、质心位置、悬挂参数等，利用SIMPACK 软件建立车辆-轨道耦合模型，通过仿真分析得出实验结论，验证突变模型的正确性与实用性，具体过程如下：

选择C64k 型列车，根据车辆的基本参数，建立车辆系统动力学仿真模型，如图3 所示。

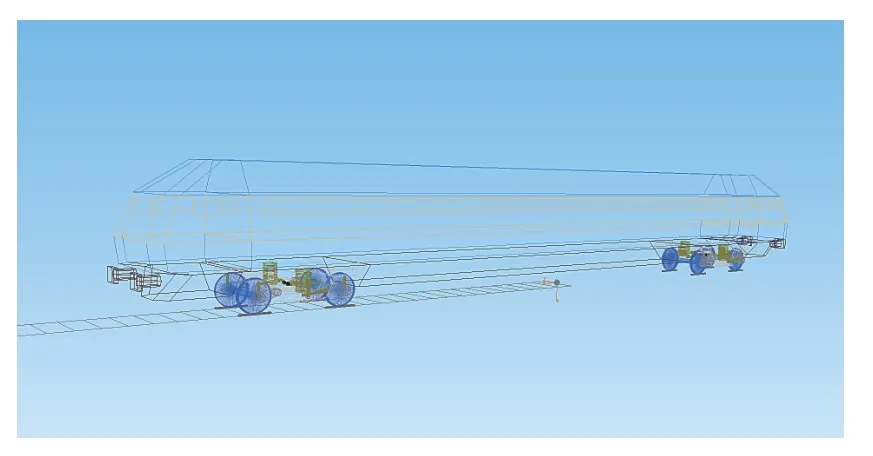
图3 车辆-轨道耦合模型

在实际线路上存在的轨道不平顺，是由不同波长、不同相位以及不同幅值的随机不平顺波叠加而成。轨道随机不平顺的统计特征只能依靠线路实地测量获得。以下是国内外典型的轨道谱，经过分析比较其特征，选取美国五、六级轨道激励谱，本次仿真选用的部分激励谱，如图4 所示。

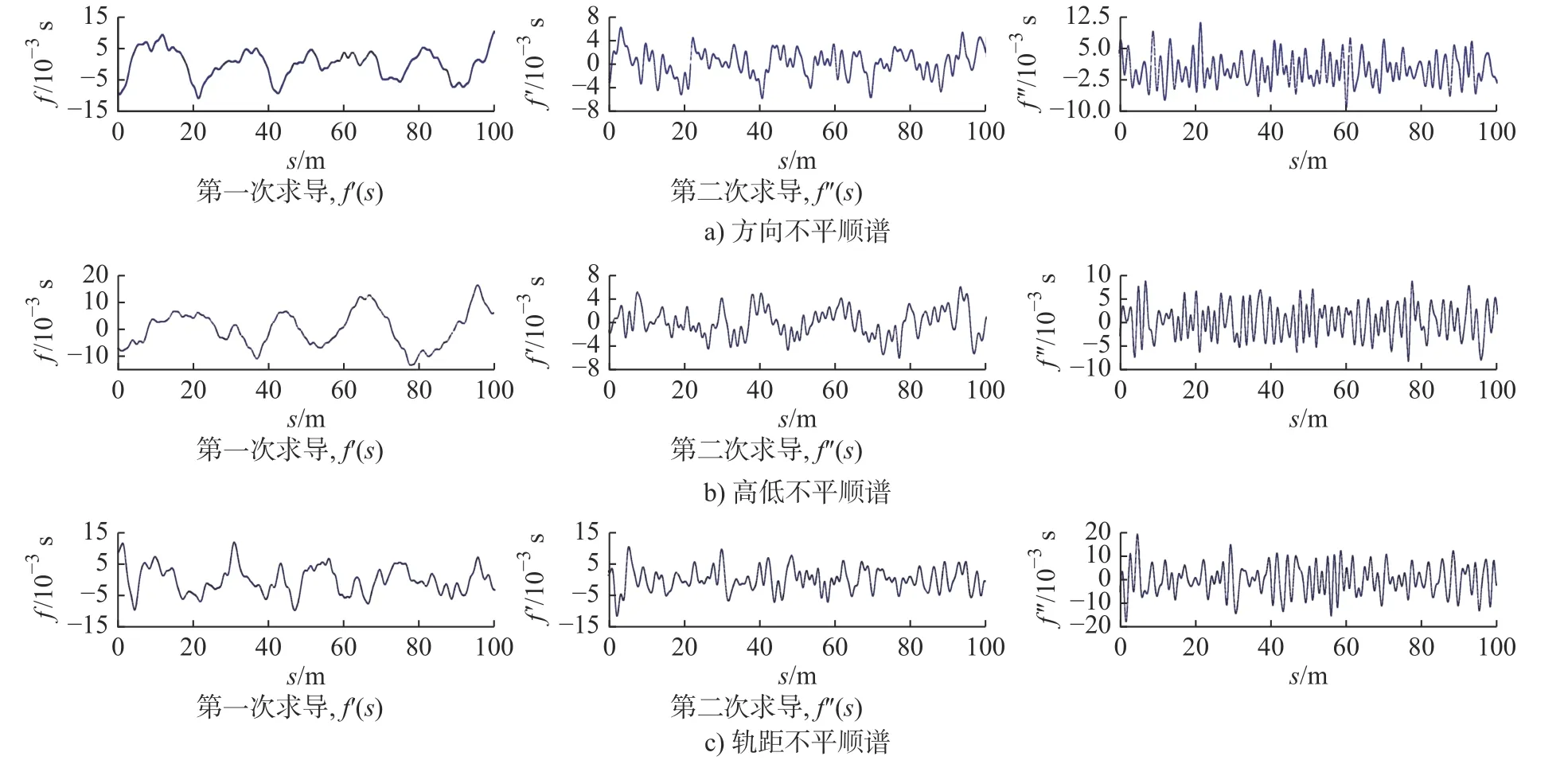
图4 美国五级轨道激励谱

将激励谱加载到轨道上，以不同级别的激励来使列车在行驶过程中得到不同的横向振动加速度，得到仿真数据，进一步分析。

3.2 数据分析

对轨道施加不同级别的路面不平顺谱，作为激励；分析不同等级的路面谱对列车运行状态的影响，以及各变量之间的关系。工况一、二分别对应激励谱：美国谱五级和六级，速度均为120 km/h，各工况车体重心偏转角时间历程、横向振动加速度时间历程和脱轨系数时间历程如图5 和图6 所示。

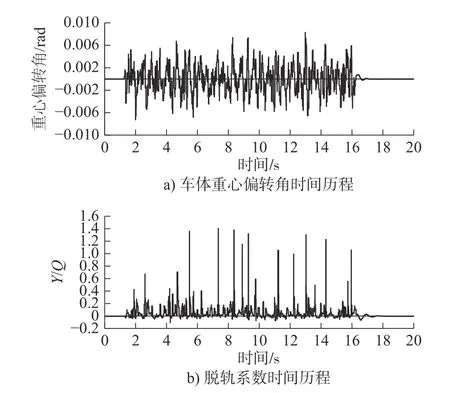
图5 工况一

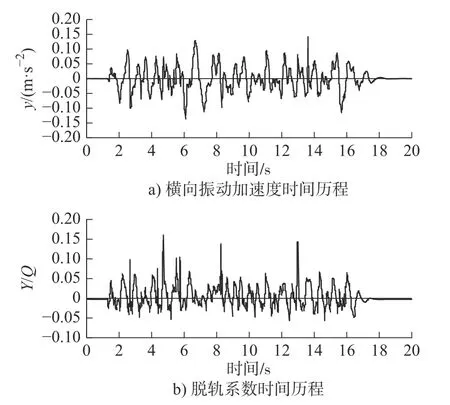
图6 工况二

由图5 和图6 可知：五级轨道激励谱较于六级，在列车运行中对横向振动加速度影响较大，部分时段的脱轨系数已经超过1.5，由于持续时间较短，已有脱轨趋势但并未造成列车脱轨。车速一定时，路面谱的等级越高，脱轨系数峰值越小，说明列车脱轨的可能性越低，运行越稳定，所以提高轨道平顺性可以减小脱轨系数，降低脱轨的可能。

由图7 和图8 可知：在不同路面激励谱下的车体重心偏转角以及横向振动加速度与脱轨系数的关系，得到横向振动加速度、车体重心偏转角与脱轨系数变化趋势相同，横向振动加速度越大，车体重心偏转角越大，脱轨系数越大，即列车脱轨的可能性增大。为了验证突变理论，做出工况一的仿真数据横向振动加速度与重心偏转角关系图。如图9 所示，当横向振动加速度由负值到正值时，此时段的脱轨系数即出现一个峰值，结合折叠突变平衡曲线与分叉集如图2 所示，首先工况二中横向振动加速度的极值分别为0.36 和−0.47，均在不稳定区域，负值到正值即为路径a→b，路径a→b为系统产生突变的路径，所以当系统横向振动加速度方向变化导致重心偏转角方向变化时，脱轨系数增大，直线运行的列车才有可能发生脱轨事故。

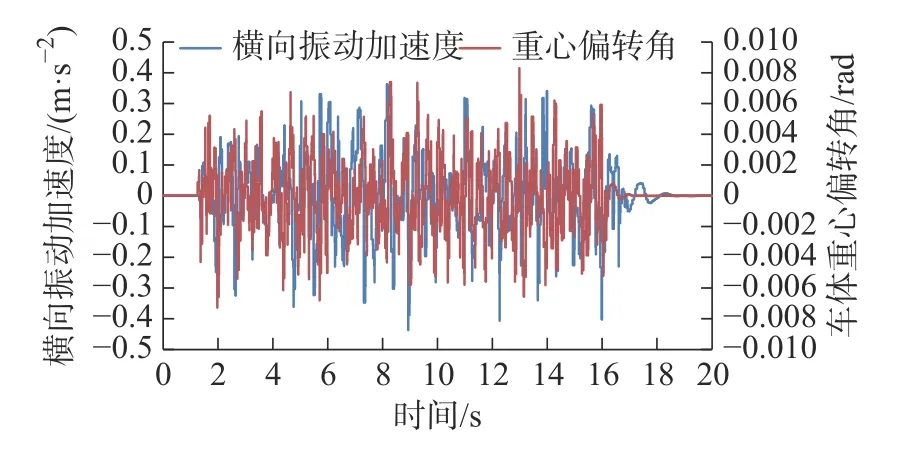
图7 工况一横向振动加速度与重心偏转角关系图

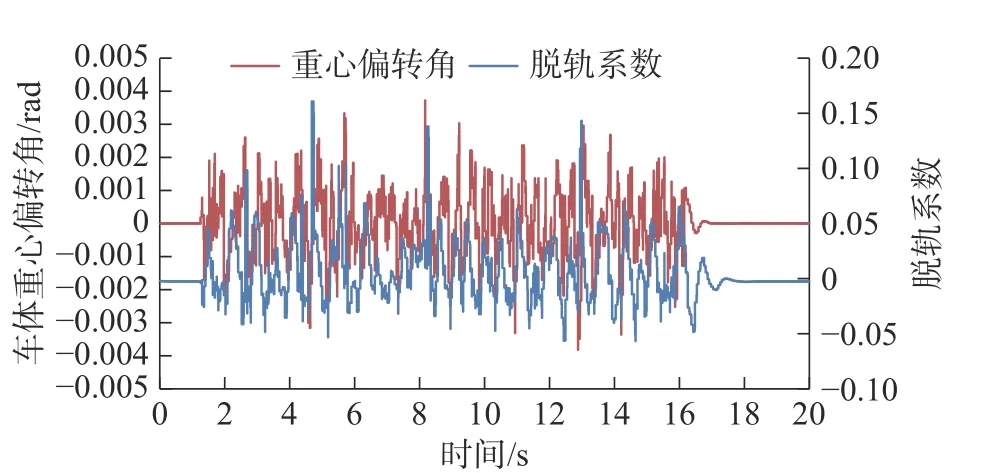
图8 工况二重心偏转角与脱轨系数关系图

图9 工况一横向振动加速度与脱轨系数关系图

4 结论

1）本文根据列车脱轨瞬间受力情况，推导出侧倾势能符合初等突变中的折叠突变模型，并通过Simpack 软件建立的仿真模型进行仿真试验研究，得到折叠突变理论可以用于列车在直线段脱轨情况的研究。

2）根据理论推导以及仿真分析得到：列车在直线段脱轨，当列车横向振动加速度增大到极值，列车重心偏转角也达到峰值，所以此时列车脱轨。横向振动加速度与重心偏转角为正相关。

3）列车脱轨问题十分复杂，影响列车脱轨的因素较多，建立更完备的列车脱轨体系以及更准确的预警方法是以后的研究重点。