一类碰撞振动系统混沌运动的QPSO-RBFNN 控制

卫晓娟，周方伟，李宁洲，丁旺才

（1.上海应用技术大学 轨道交通学院，上海 201418；2.兰州交通大学 机电工程学院，兰州 730070）

在机械设备、机车车辆等实际工程系统中由于间隙的存在，使得该类系统在外激励作用下会产生混沌振动[1]，导致机械部件磨损或引起噪声。因此，为保证机械系统的运行安全以及对噪声进行有效的控制，使得对混沌运动的控制就显得尤为重要。

国内外研究者从解析方法和数值模拟方面对碰撞振动系统混沌运动形成机理及控制问题进行了广泛的探索和研究[2-6]。田亚平等[7]用改进的OGY 方法，实现了含齿侧间隙和轴承支承间隙的单级齿轮系统混沌吸引子内部不稳定周期轨道的稳定化。张曹辉[8]采用经PSO 优化的SVM 方法，分别对含间隙单自由度刚性碰撞振动系统及弹性碰撞振动系统的混沌进行控制。李松涛等[9]采用脉冲控制方法实现了混沌运动控制，最终控制为稳定的周期运动。林何等[10]以轴承预载荷为摄动激励实施微扰控制，以实现多间隙齿轮-轴承系统的混沌吸引子向多种不同周期路径上的迁移控制。Lee 等[11]提出了一种依据反馈控制思想的策略，从而实现了对一类碰撞振子位置进行控制。杜伟霞等[12]采用间歇控制方法实现了两自由度弹碰系统混沌运动的控制。Shen 等[13]采用实时离散时间反馈控制策略，将擦边引起的混沌抑制为1/n周期运动。张惠等[14]采用RBFNN 方法实现了单自由度弹碰系统的分岔及混沌的控制。卫晓娟等[15]采用动态多子群引力搜索算法优化的脊波神经网络实现了混沌运动控制。

文献[16]提出一种基于AHGSA 算法优化径向基函数神经网络（Radial basis function neural network，RBFNN）的混沌控制方法，虽然取得了较好的控制效果，但是控制器参数优化算法（AHGSA 算法）需要进行混沌初始化及变异操作，其算法结构相较复杂，且AHGSA 算法本身的控制参数较多（有3 个控制参数），所以该方法在控制器参数优化算法配置方面还有改善的空间。因此，本文采用结构相较AHGSA 算法更为简单、控制参数也仅有一个收缩-扩张系数β的QPSO（Quantum particle swarm optimization）算法[17]，提出一种基于QPSO 优化RBFNN 的参数反馈混沌控制方法:将最大Lyapunov 指数、Poincaré截面上相邻两点间的距离、以及控制器输出量一起作为加权项，构建适应度函数以引导QPSO 算法完成控制器参数的优选，并对β采用了非线性自适应调整策略来进一步提升QPSO 算法的寻优效率。仿真实验结果验证了该控制方法的可行性及有效性。

1 系统力学模型及混沌运动

本文研究图1 所示系统的混沌控制问题。图1中，水平支撑面为光滑平面，质量块在简谐激振力Psin(ΩT+τ)作用下振动，运动的位移用X表示，当质量块位于平衡位置时，其与右侧刚性约束的间隙为H。图1 中：M为质量（质块）；C为阻尼系数（线性阻尼器）；K为刚度（线性弹簧）。

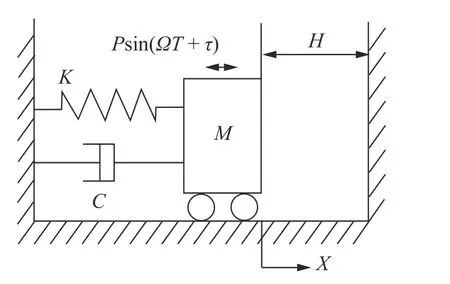
图1 含间隙单自由度刚性碰撞振动系统力学模型

当质块M与右侧刚性约束发生碰撞时，其运动位移为H。若碰撞持续时间忽略不计，则图1 系统运动微分方程为:

为揭示一定参数条件下图1 系统的混沌运动产生机理，选择碰撞后瞬时的 σ截面（即σ=其中θ=ωtmod(2π)）为Poincaré截面。分别在①ζ=0.20，R=0.80，h=0.05，②ω=2.65，R=0.80，h=0.05 条件下，研究混沌运动与系统参数（简谐激励力频率ω、阻尼比ζ）之间的关联关系及表现特征。图2 为在Poincaré截面上质块速度随ω和ζ变化的分岔图及Lyapunov指数谱图。由图2a）可知，当ω∈[2.50，2.56]时，系统具有稳定的周期1-1 运动（符号n-p中n代表激励周期数，p代表碰撞次数），随ω逐渐增大，系统由周期1-1 运动经历倍化分岔序列，演变为周期2-2运动、4-4 运动、···、直至混沌；但当ω继续增大，混沌运动又退化为周期运动。由图2b）可知，当ζ∈[0.2，0.43]时，系统为混沌运动，当ζ∈（0.43，0.56]时，系统退化为周期4-3 运动，当ζ>0.56 时，系统为周期2-1 运动。Lyapunov 指数作为一个定量指标[18]，在图2 中也直观地表明了系统运动形态变化与ω、ζ之间的关系。图2 中，最大Lyapunov 指数用 λ1来表示。当λ1<0时，该系统为稳定的周期n-p运动；当λ1>0时，该系统为混沌运动；当λ1=0、而λ0<0时，系统发生倍化周期分岔。

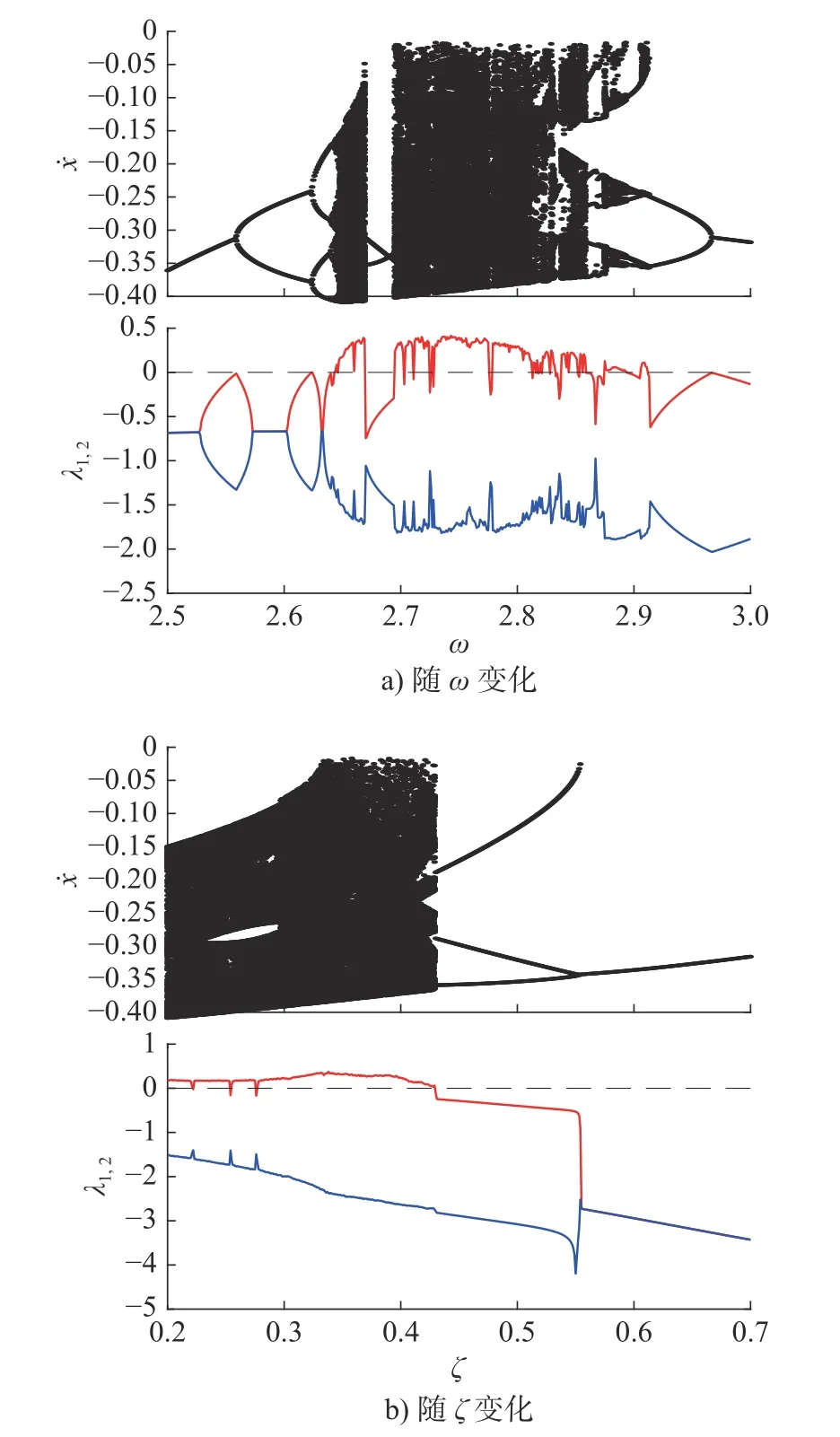
图2 系统分岔图和Lyapunov 指数谱图

图3 为当ω=2.65，ζ=0.2，R=0.8，h=0.05 时的混沌吸引子和相平面图。由图3a）可看到，在Poincaré截面上为成片的散落点集，且有层次结构；由图3b）也可以看到，此时系统相平面图非常复杂且不重复；图3a）和图3b）均揭示了该系统运动为混沌运动。

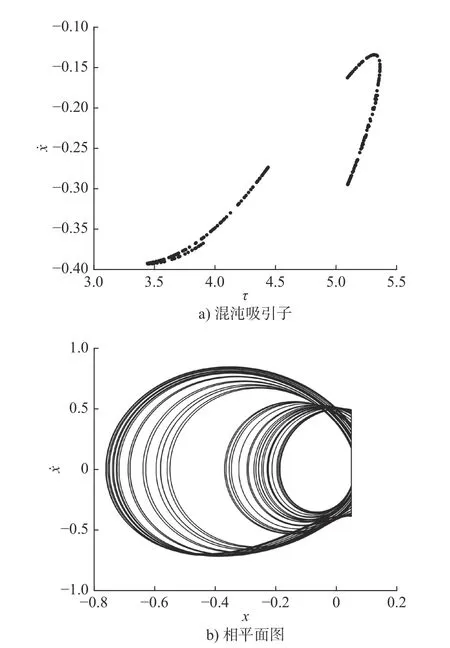
图3 混沌吸引子和相平面图（ω=2.65）

2 RBFNN 混沌控制器设计

现有的一些碰撞振动系统混沌运动控制方法需要获知系统模型信息，在受控系统模型未知或难以精确得到时将很难适用。而工程实际中，混沌系统极其复杂，模型信息通常未知或难以精确得到。为此，本文基于RBFNN 设计混沌控制器，在控制器设计时不使用被控系统数学模型信息（文中利用系统模型仅为了产生I/O 数据），也即控制器设计与系统模型的阶次、结构及参数等无关。

本文所设计的混沌控制器结构如图4 所示。将能够反映系统趋近于稳定周期运动趋势的相邻两次迭代后Poincaré截面上的投影点间的距离（即d(k)=∥X(k)−X(k−1)∥,d(k)=∥X(k−1)−X(k−2)∥；X（k）为第k次迭代后被控系统状态变量X=[,τ]的值）作为控制器输入。

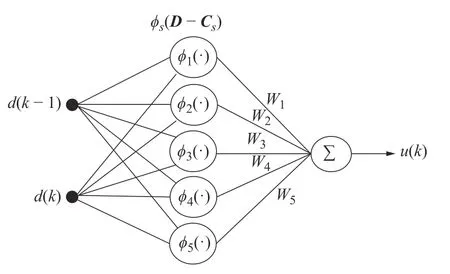
图4 控制器结构

3 QPSO 优化控制器参数

混沌控制器的参数选择不同，导致控制效果产生较大差异，从而影响其控制性能。控制器参数的选择方式也会影响控制系统设计效率。现有方法中，控制器参数主要依靠人工经验进行选定。本文采用QPSO 算法优化选择控制器的参数，减少了设计控制器时对主观经验知识的依赖，有助于提高控制系统设计效率。

QPSO 算法中只有一个控制参数β，结构简单，且为提高算法全局探索能力，引入粒子平均最好位置。使得各个粒子在搜索过程中存在等待效应，提高了粒子间协同搜索能力。因此，本文所设计的混沌控制器的参数优化选择采用QPSO 算法。

3.1 适应度函数的构建

适应度函数可引导QPSO 算法优选控制器参数，同时也可定量评价混沌控制器的控制能力。本文选定最大Lyapunov 指数及相邻两次迭代后Poincaré截面上投影点间的距离作为判断依据。考虑对混沌运动进行控制时控制能量消耗最小（实际系统中，控制器输出能量总是有限的），构建控制器参数优化选择时所应满足的适应度函数为

式中：αr为相对权重，r=1，2，3；X（k）为受控系统状态变量X在k时刻的值；η为在区间（0，1）上均匀分布的随机数；u（k）为控制器输出；d∗为Poincaré截面上相邻两点距离的期望值。

3.2 QPSO 优化控制器参数步骤

采用QPSO 算法使适应值函数取得相对最小值的全局最优解，即是混沌控制器的最优参数。该算法的参数设置为：种群规模m=30，粒子最大搜索次数为100 次，收缩-扩张系数β=0.8 − 0.2*sin（π*itercur/itermax）（itercur为粒子当前搜索次数；itermax为粒子最大搜索次数）。第i粒子的第j维的t时刻位置表示为Xi,j(t)，个体最好位置表示为Pi,j(t)，群体的全局最好位置表示为Gj(t)。QPSO 算法中粒子位置更新方程为：

QPSO 算法的执行过程如图5 所示。

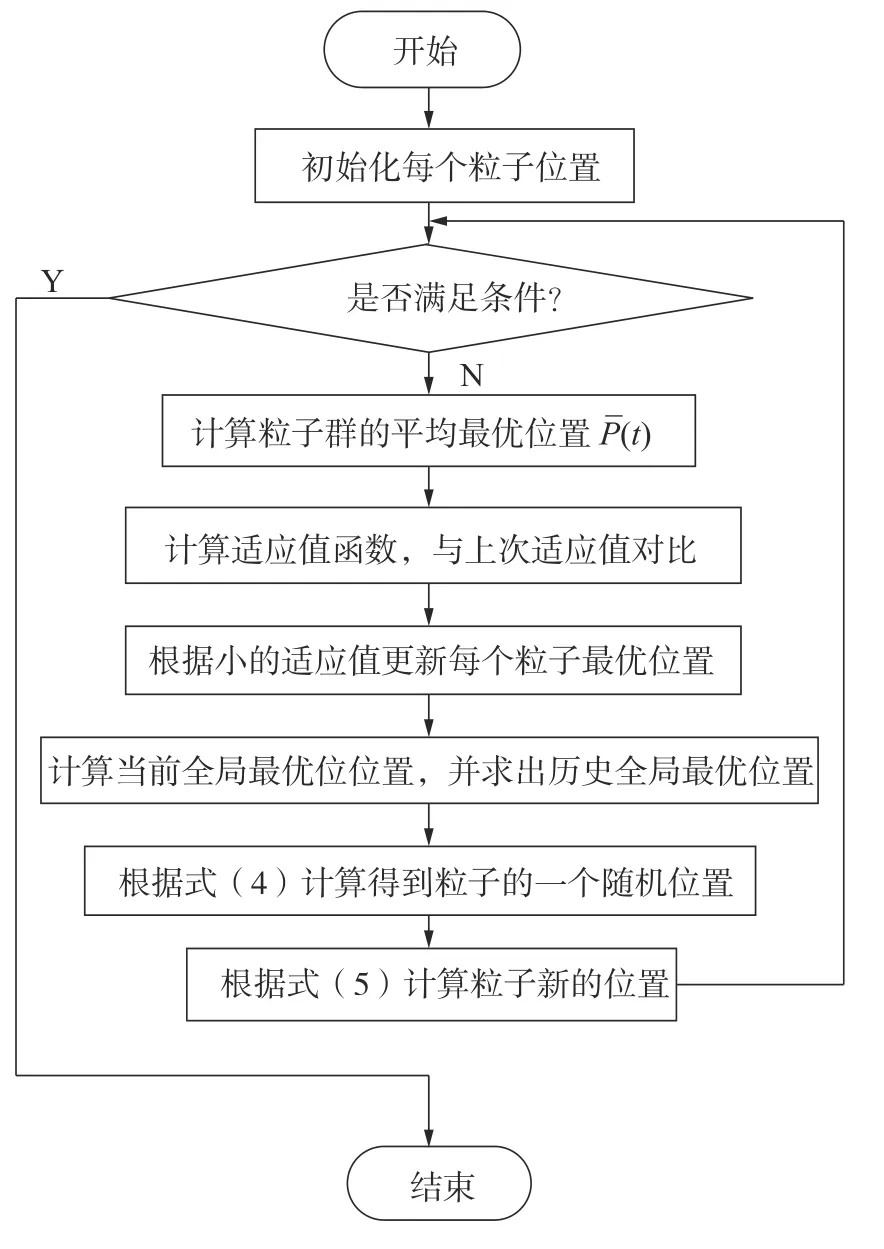
图5 QPSO 算法流程

4 仿真研究

4.1 混沌运动的控制结果

采用QPSO-RBFNN 方法对图3a）所示的混沌吸引子进行控制。控制器设计不依赖于系统模型信息，仅利用系统模型产生I/O 数据。针对系统可控参数ω（激励频率）或ζ（阻尼比），对其施加微小扰动，从而将混沌运动控制为目标周期1-1 运动及周期2-2 运动。为了呈现该控制器对混沌的控制效果，在系统迭代400 次时施加控制。

图6 为u（k）=Δω时混沌运动仿真结果图。由图6a）～ 图6d）可知，混沌运动迅速被控制为周期1-1 运动，相图为一条封闭曲线，且此时 λ1从正值（系统运动为混沌运动）逐渐变为负值（系统运动为稳定的周期运动）。由图6e）～ 图6h）可知，混沌运动迅速被控制为周期2-2 运动，相图为两条封闭曲线，λ1从正值逐渐变为负值。

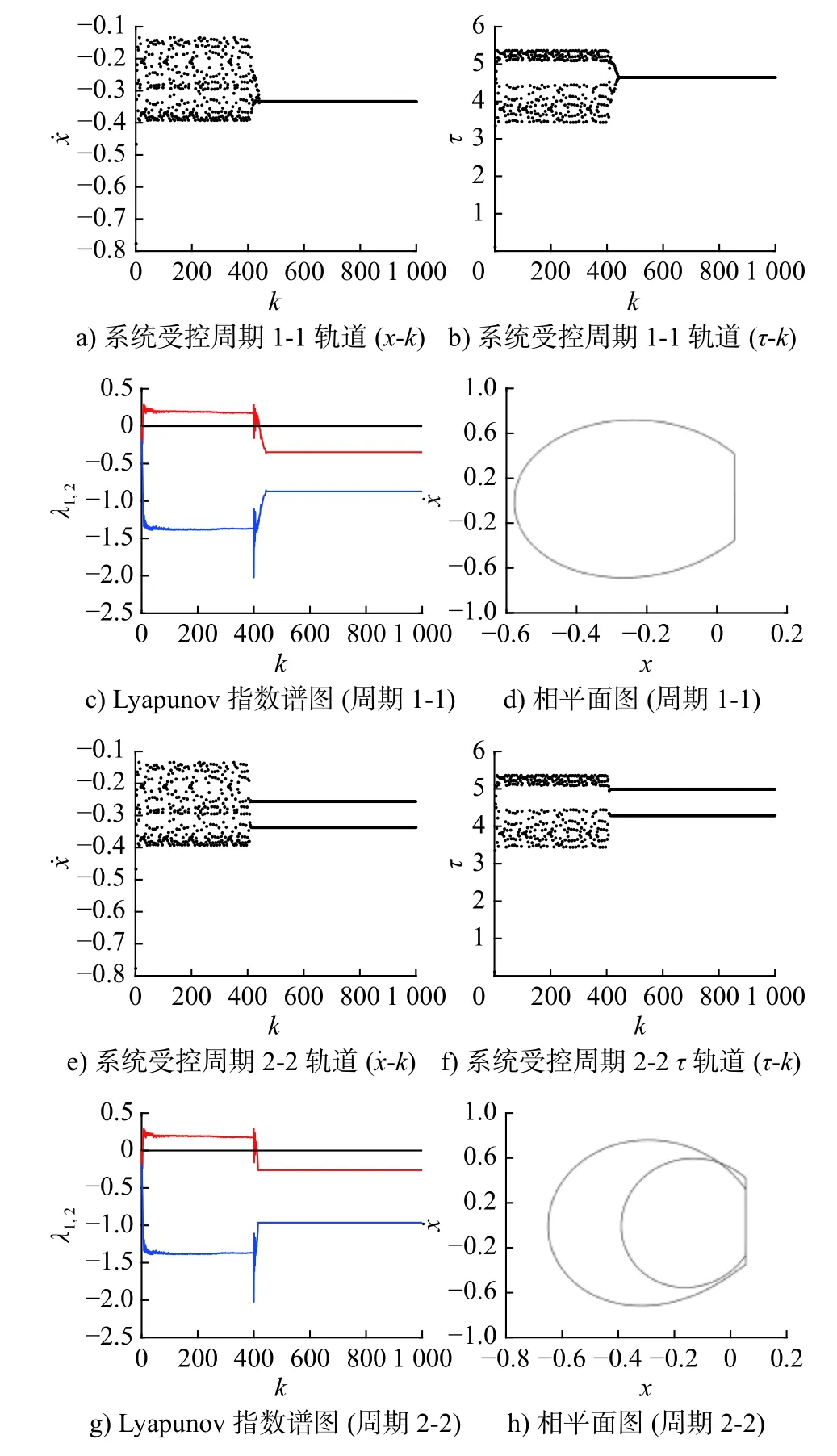
图6 u（k）=Δω 时，系统的受控周期运动

表1 和表2 分别为周期1-1 和周期2-2 中QPSO 算法优化后的混沌控制器的参数。

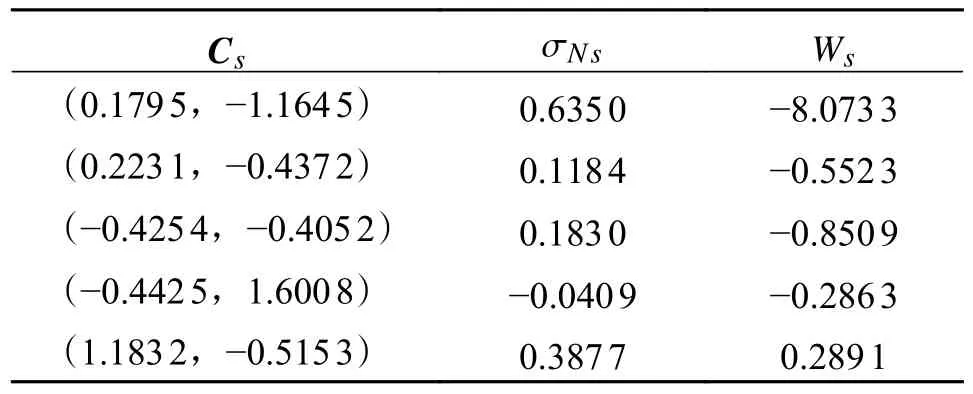
表1 混沌控制器参数（周期1-1）

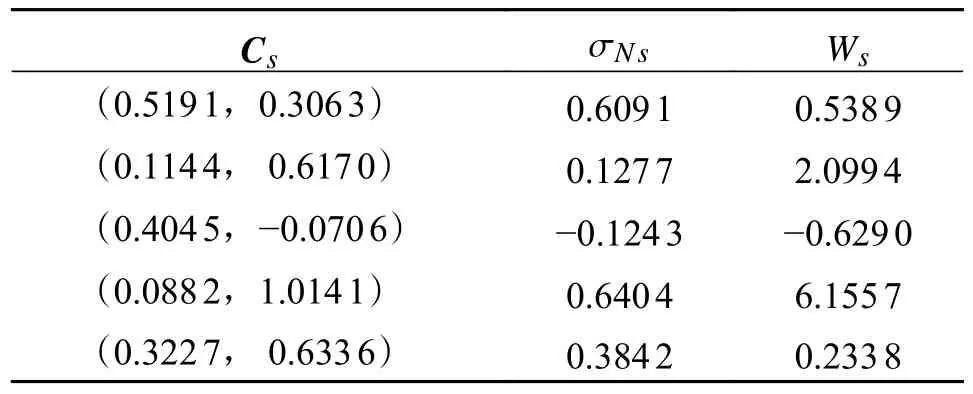
表2 混沌控制器参数（周期2-2）

由上述仿真结果可知，本文所设计的控制器有效的控制了图1 系统中的混沌运动，并实现了混沌运动控制预期目标为周期1-1 运动以及周期2-2 运动。由图2 中的分岔图可知预期控制目标可以为其他周期轨道，但出于篇幅的考虑，其余周期轨道不再赘述。

图7 为u（k）=Δζ时混沌运动仿真结果图，结果表明混沌运动很快被控制为周期2-1 运动、周期4-3 运动，相图和Lyapunov 指数谱图也表明混沌运动被控制为稳定的周期运动。

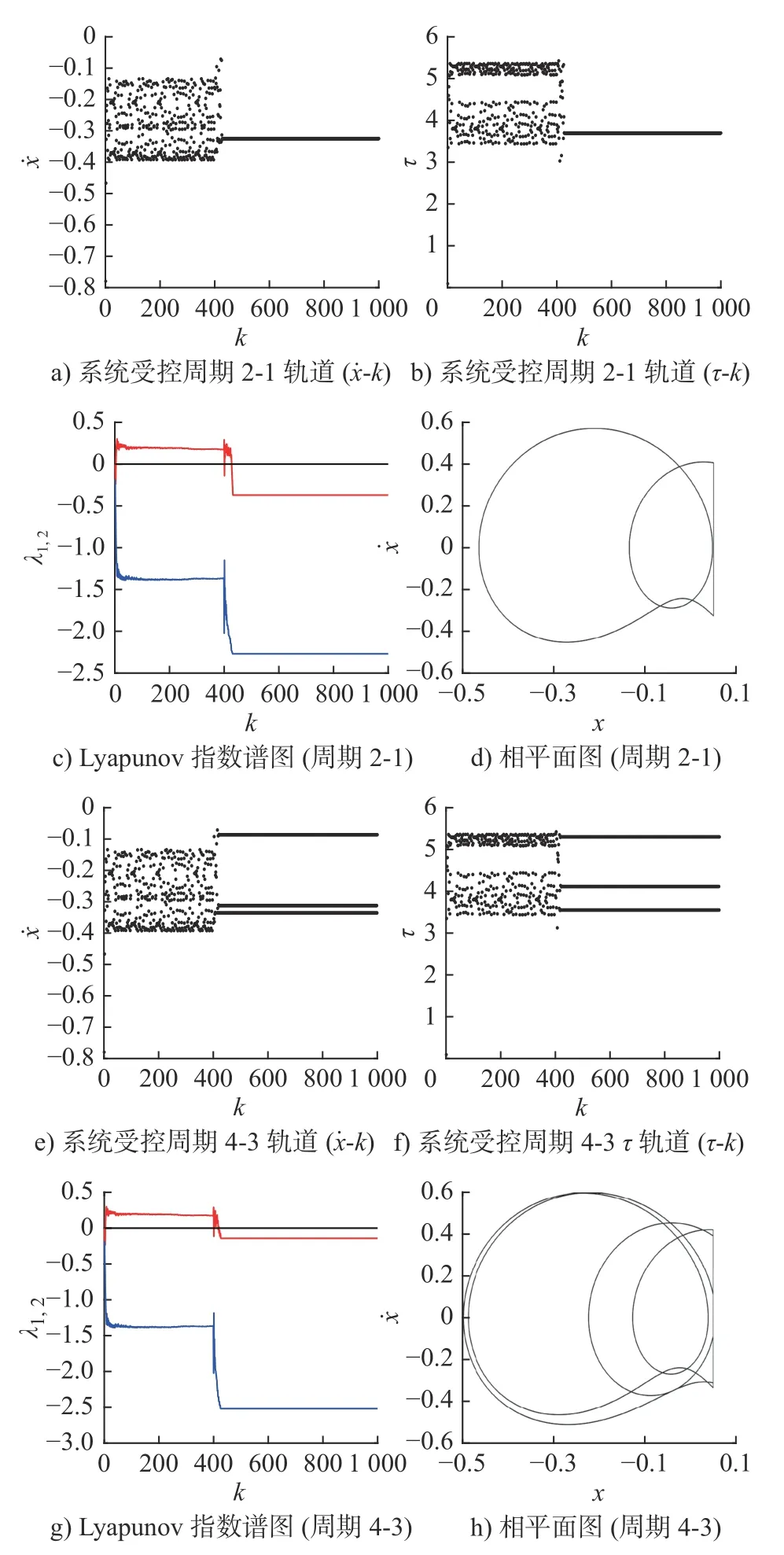
图7 u（k）=Δζ 时，系统的受控周期运动

采用QPSO 算法优化后的混沌控制器参数如表3（周期2-1）、表4（周期4-3）所示。

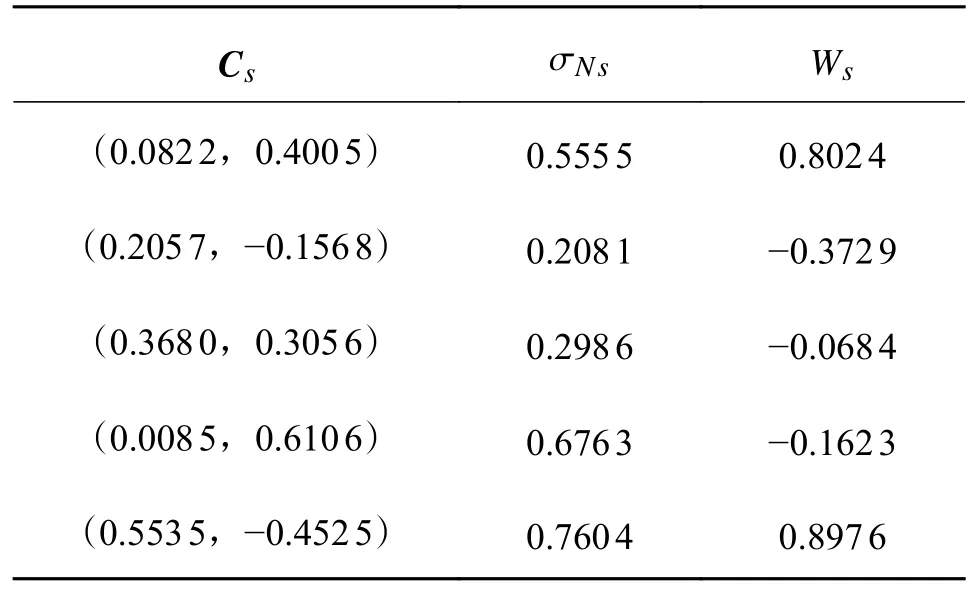
表3 混沌控制器参数（周期2-1）

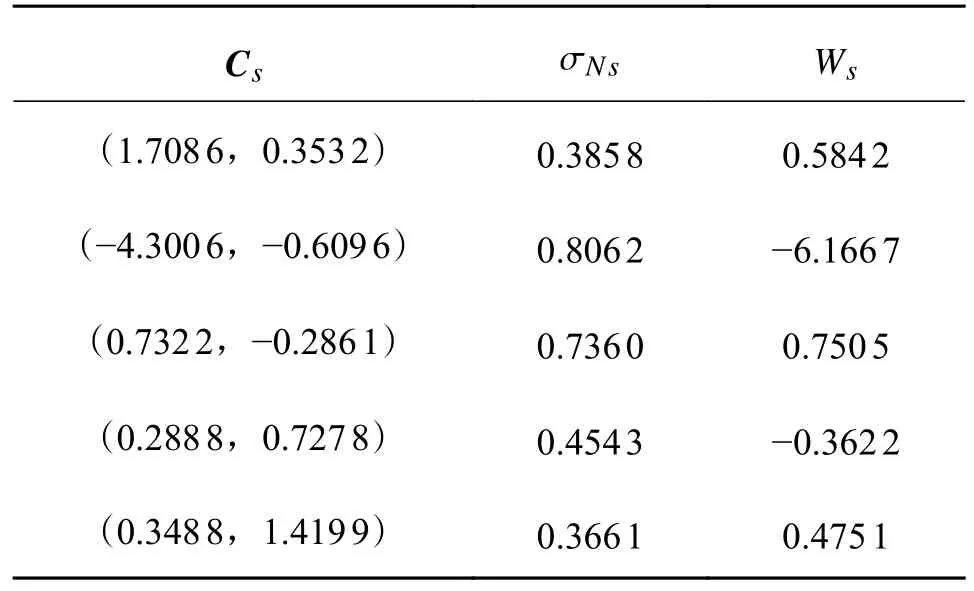
表4 混沌控制器参数（周期4-3）

4.2 QPSO 中的β 取值对控制效果的影响分析

收缩-扩张系数β作为QPSO 算法中的唯一参数，其不同的取值方式对算法的寻优能力产生较大影响。在QPSO 算法中，β取值越大，算法的全局探索能力越强，且收敛快；β取值越小，算法局部开发能力越强，但收敛慢。为了实现全局探索和局部开发能力的平衡，本文选用3 种确定β取值的方法（固定取值法、线性递减取值法、非线性取值法）进行实验：β=0.6或0.8 ；β=0.8−0.3∗itercur/itermax；β=0.8−0.2sin(π∗itercur/itermax)。实验目的为将图3a）所示混沌吸引子控制为稳定的周期1-1 运动，且控制器输出均为u(k)=∆ω。3 种不同β取值下仿真结果如图8 所示，仿真结果的描述如表5 所示。

表5 β 不同取值下的系统运动描述

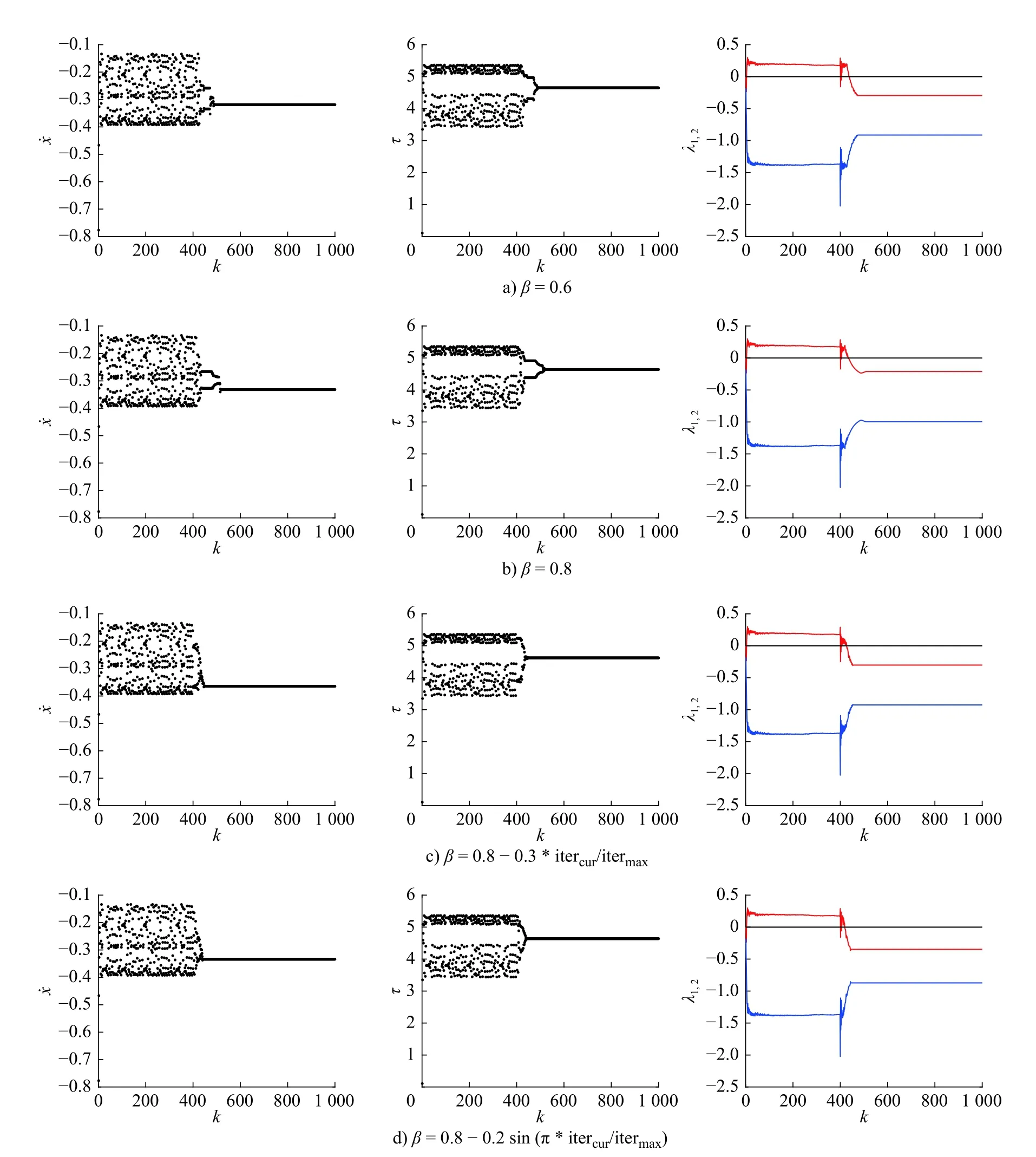
图8 收缩-扩张系数β 的3 种不同取值方法下的轨道图及Lyapunov 指数谱图

由图8 和表5 可知，β的3 种取值方法均可保证达到预期的控制目标，但相较而言，β为非线性取值时，控制更为快速高效，说明此时QPSO 算法寻优效率相较更高，搜索到的控制器参数确保了混沌控制器能够很好地学习被控系统的非线性特性，从而使得系统能够在相较更短的时间内即可自动搜索到预期的稳定周期轨道。

5 结论

本文提出了一种基于QPSO 优化RBFNN 的混沌控制方法。通过对Lyapunov 指数谱图、Poincaré截面图等结果分析，获取了分岔及混沌的参数分析判据以确定控制器输入/输出变量，并据此建立了适应度函数以实现对控制品质的量化评价（适应度函数值的变化反映了混沌控制效果）。仿真结果表明，所建立的适应度函数能够很好地引导QPSO算法搜索到相对最优的控制器参数，且β为非线性取值时QPSO 算法寻优效率相较更高，搜索到的控制器参数确保了混沌控制器能够很好地学习被控系统的非线性特性，使得控制更为快速高效。