油气管道智能封堵机器人新型双球面连接器研究

唐洋，刘祥，吴杰，王远，熊浩宇

（1.西南石油大学 机电工程学院，成都 6 105002；2.南方海洋科学与工程广东省实验室，广东湛江 524088）

油气能源是国家战略性能源储备的必要能源之一，其重要性不言而喻[1-3]。油气输送则是油气开采环节中必不可少的，管道机器人是管道作业中重要工具，在狭窄的管道作业中，若机器人设计为一个整体，对尺寸要求会极其严苛。若设计尺寸不合理，在管道过弯和焊缝等内径突变处容易卡堵，影响管内的流体输送，直接或间接造成重大的经济损失。长度较长的管道机器人会被拆分成若干个单元节，每节一般采用柔性、刚柔耦合的零部件进行连接[4]，图1 为管道智能封堵机器人且采用新型过线连接器连接。

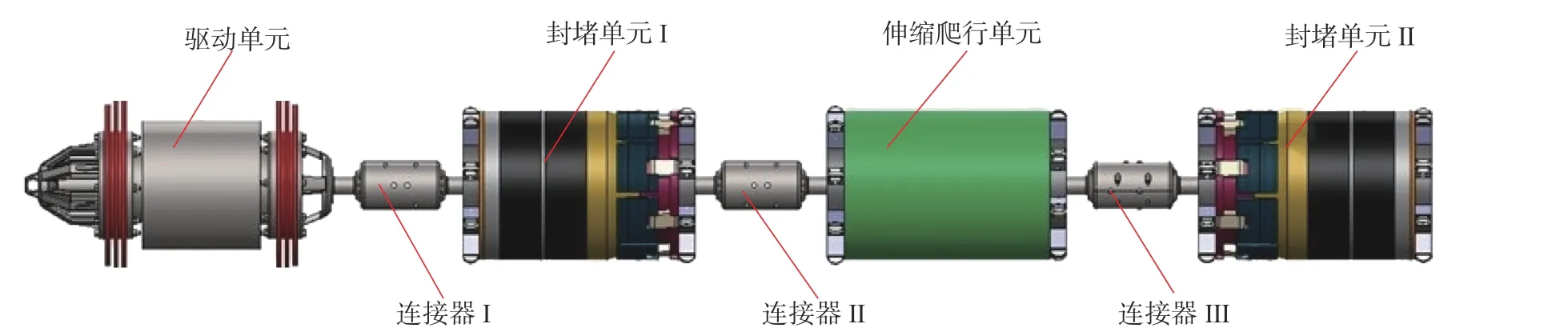
图1 管道智能封堵机器人

现有的管道机器人中都是用的传统连接形式，如用十字轴向连接器、虎克铰和球铰等连接[5-8]。这些连接形式广泛运用于铁道车辆，RPC 球铰应用于大吨位桥梁转体及墩顶转体[9-10]、航空机构连接和机器人拇指和手掌关节，增强了手指弯曲转动的灵活性及医疗器械等机械装置的连接中[11-13]。颜惠华等[14]推导了球铰摩阻力矩和静摩擦系数计算公式，进行静摩擦系数与实际牵引力反推计算得到的静摩擦系数吻合较好。范剑锋等[15]基于非赫兹接触理论来进行球铰磨心二维及三维状态下接触应力的计算，并通过与实际测量结果及实际工程数据的比较，得出相对于现行规范的简化算法。张玺等[16]采用基于赫兹接触理论分析了柱塞与导向套接触状况，研究了球铰允许摩擦圆半径的计算方法，根据球铰摩擦圆半径与球铰结构的关系，提出球铰结构参数的确定方法。宋海生等[17]提出了一种基于微动滑移摩擦理论的后视镜球铰能量耗散模型，并推导出球铰微滑移干摩擦产生的能量耗散公式。张亮亮等[18]搭建了试验台，对俯仰摩擦阻力矩进行实验测试，推导了力矩与摩擦因数的关系，求得了球铰的实际摩擦因数。

前者已对单球铰的接触或动力学有了一定的研究，但是缺少此类连接器的创新设计，同时更没有学者对多重球面抱合、内部过线的此类连接器开展研究。本研究创新出双球面抱合的球铰连接器，可解决单球面接触下磨损严重问题，同时提高转动灵活性，具有过线功能。同时进行动力学仿真，分析连接器轴向载荷对转动角速度的影响。进行转动实验，来验证装置样机的转动性能、过线性能和内部过线的损伤情况。

1 双球面球铰接触模型

与平面接触相比，球面接触计算更加复杂，对于球铰关节内的接触力，它会影响构件之间的接触和摩擦状态，从而决定球转动的效率[19]，设计方案及相关参数如表1 和图2 所示。

表1 45 号钢连接器尺寸

对球铰摩擦接触模型进行假设：接触区发生小变形；接触面呈椭圆形；相接触的物体可被看作是弹性半空间；接触面上只作用有均布的垂直压力；间隙为无穷小，碰撞效应可以忽略；整个球面润滑情况相同，即摩擦表面的摩擦因数处处相等。

1.1 接触应力理论模型

由于连接器球铰的上下球铰半径非常接近，采用赫兹接触应力方法进行分析时，发现计算得到的Rm值近似于0，因此球在球座中的应力不再适用于连接器球铰，由弹性力学知识可知[20]，半平面体在边界上作用集中力时，径向应力的表示式为

式中R为接触球面半径，mm。

半平面体在边界上作用集中力时，径向应力与cosθ成正比，因此参考上述结论，连接器球铰接触面上 的正应力与cosθ成正比，如图3 所示。

图3 转向连接器受拉和受压情况下端球铰处接触应力

应力可表示为

式中：Rm为接触圆面半径，mm；P为外部压力，N。

径向应力的竖向分量沿球面积分为上部结构荷载P，本方案的模型的接触球面为弧形带，因此φ的取值范围为β∼π/2。

1.2 转动摩擦理论模型

建立坐标系，原点与球壳体的中心点重合，XY平面为过球铰中心的水平面，Z轴竖直向上。对应XYZ坐标系建立相应的球坐标系，分别将球坐标θ、β、θ1和β1等分，将球面离散，如图4a)所示。球面上任意一点与回转中心X轴的关系如图4b)所示。

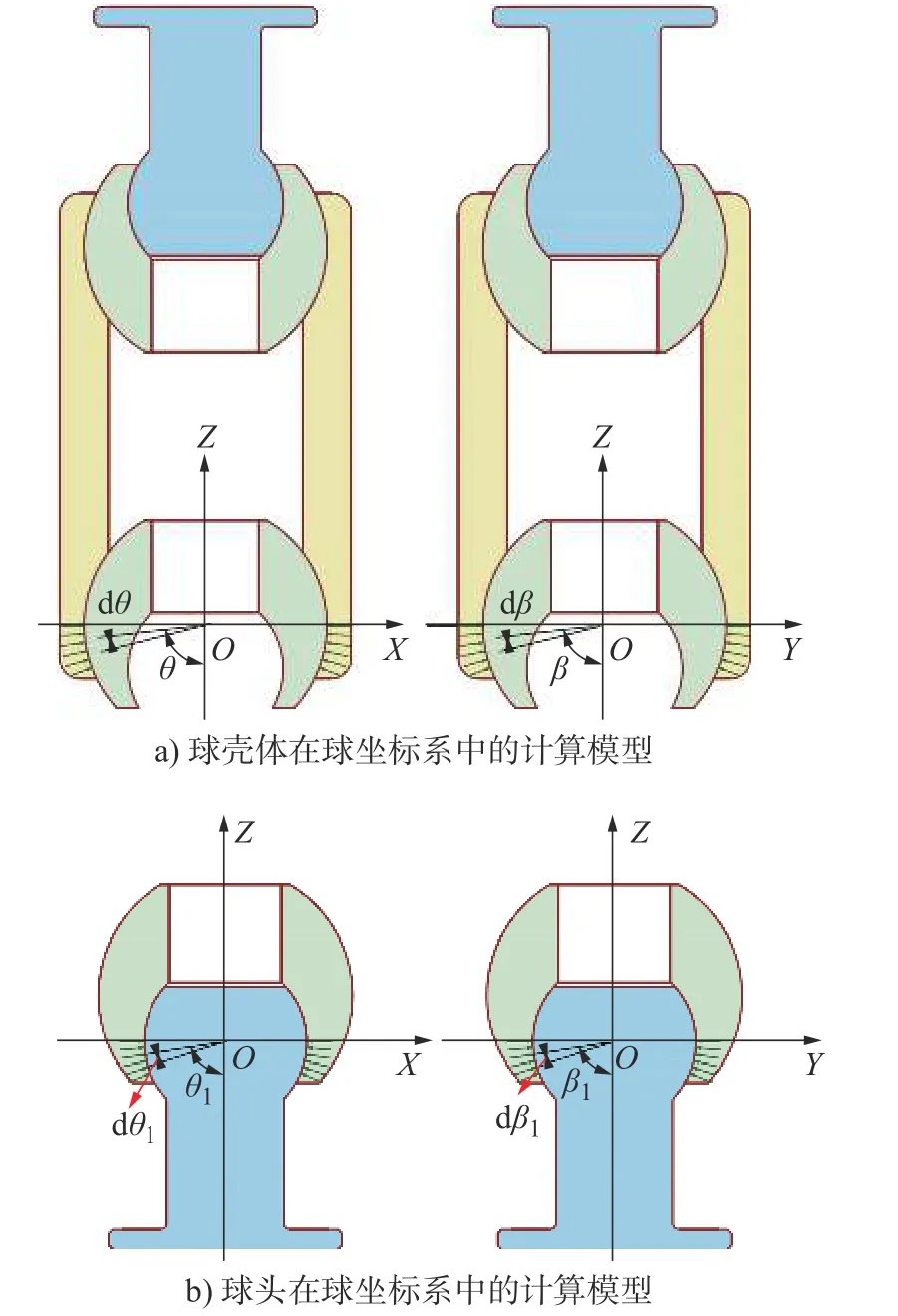
图4 连接器转动摩擦模型

在计算模型中，取微圆XOZ平面上，取夹角值为 dθ，所得到的弧长值为rdθ。此时，此弧长的接触线也是一个圆弧，在其上取微夹角 dβ，夹角对应的旋转半径为rsinθ，对应的弧长为rsinθdβ，接触面所得到的微单元面积A=rsinθdβ×rdθ。

球铰接触面在安装前充分研磨，保证球面接触率不低于75%[21]。P0为沿法线方向上的接触应力，当 θ=90°时，P0刚好为最高点处的接触力。所以当微单元面沿法线方向上的正应力为

式中r为球铰半径，mm。

根据实际工况，球铰模型简化为以过球心的水平面为基准面，当受到拉力时：转动运动中基准面下方的球面受到正压力和摩擦力，基准面上方的球面不受力；当受到压力时：转动运动中基准面上方的球面受到正压力和摩擦力，基准面下方的球面不受力。由此 θ的取值范围[α∼π/2]，β的取值范围[0∼2π]，为圆弧中心角余角，积分得到

式中α 为球铰中心角之半，（°）。

在计算球铰转动摩擦力矩时，球铰沿X轴旋转，设球铰半径与旋转半径夹角为ϕ，于是可以得到摩擦力的力臂L=rcosϕ，正应力在力臂上的分力为dFNcosϕ，摩擦力dFf=µFNcosϕ，可推出球铰上任意一点摩擦力对X轴的摩擦力矩为

式中:Mf为球铰转动力矩；FN和Ff分别为法线竖直方向的正压力和微元表面摩擦力，N；L为摩擦力力臂，mm；µ为球铰静摩擦因数。

球铰受到两部分摩擦力：上端与上凹面接触摩擦；下端与下凹面接触摩擦。由于球铰半径与旋转半径夹角ϕ=θ，摩擦力矩的积分范围与正应力的方向相同，所以积分得到一对接触面的摩擦力矩为

2 新型双球面连接器转向多体动力学分析

对连接器进行动力学分析，测量转动角速度等重要参数，以此来评价连接器的转动灵活性，模拟实际工况中，连接器两端连接设备过弯。仿真计算过程中，设置步数500，计算时间0.8 s。每个接触对的接触和摩擦参数（如接触刚度、力指数和摩擦因数）是输入参数，径向作用力（输出扭矩）和轴向力施加到两端的球头杆端面作为输入，然后可以获得球头杆的转动角速度、角加速度和偏转角度，壳体的转动速度和偏转角。

2.1 仿真结果及分析

多体动力学仿真，添加−10 N 的轴向力，以恒定2 N 的切向力进行计算。过线转向连接器运动主要分为两个先后的过程：其一，在切向力的作用下球头杆先被推动转动到极限位置，球头杆撞击到球壳体速度降低；其二，球头杆和球壳体共同转动，到0.4 s时两者到达极限位置接触到上下壳体后停止转动，如图5 所示。

图5 过线转向连接器运动过程

仿真结果表明的连接器工作过程中，球头杆小球面接触面转动阻力小于球壳体大球面转动阻力，出现了先后转动的情况，相较于单球面的球铰，此连接器可以满足小转角的弯管段，同时需要的转动力矩也会相对较小，转动灵活。

2.2 轴向载荷影响

机器人在管道内运行通过弯管段时，新型双球面连接器前端部分会受弯管影响速度降低，装置后端部分速度还保持原始的速度，此时新型双球面连接器受到后端部分的轴向推力。因此，仿真分析中考虑轴向力，仿真模型两端加入−5 N、−10 N 和−15 N的轴向力。

对于球头杆的转动影响较小，在0.19 s 时，球头杆转动极限位置，开始推动球壳体转动。轴向力为−5 N 时，角速度最大，新型双球面连接器在0.35 s转动极限位置；轴向力为−10 N 时，新型双球面连接器在0.45 s 转动极限位置；轴向力为−15 N 时，角速度最小，新型双球面连接器在0.55 s 转动极限位置，如图6 所示。在轴向不同载荷的加载下，连接器克服阻力转动，初始的转动力矩分别为：0.3 Nm、0.58 Nm 和0.7 Nm。在载荷15 N 的时候，最大阻力矩峰值为1.5 Nm。由于仿真中，当球头杆转动由于惯性作用撞击到球壳体，此时球头杆推动球壳体整体转动，测量值出现波峰，导致转动过程中阻力大小波动幅度较大稳定性较差，但仿真结果的整体趋势和参数较为准确且符合设计要求，如图7 所示。在0.5 ～ 0.2 s 时间段的曲线，很好的反映了载荷工况下的转动力矩影响规律。

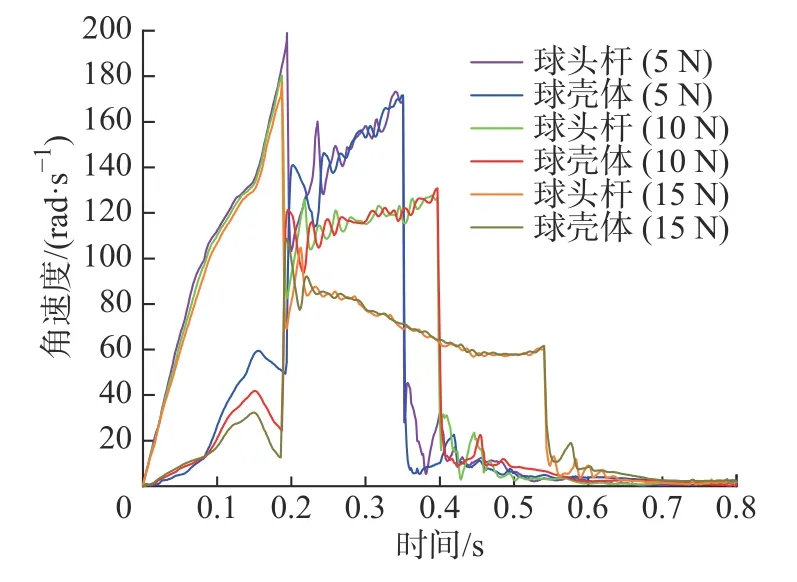
图6 球头杆和球壳体角速度

图7 不同载荷下转动力矩变化情况

3 新型双球面连接器加工与性能实验

新型双球面连接器采用双层球面，可以施加很小的力矩推动球头杆完成最大限度的偏转角度。因此对于新型双球面连接器的转动力矩的测量是十分有必要的，可以判断新型双球面连接器转动的灵活性，如图8 所示。

图8 连接器转向角度对比

推拉力计连接电脑测量实时拉力大小，圆头支撑杆在绝对的钢板上滑动，忽略摩擦力的影响，如图9 所示。

图9 实验过程

实验中，用推拉力计以恒定的速度，平缓拉动施力钢杆直到新型双球面连接器转动到极限位置，同时观察电脑上的实时拉力大小，多次重复上述实验，直到出现较为稳定且合理的测量拉力大小，如图10所示。拉力大小变化主要分为两个阶段，2.40～ 5.7 s，推拉力计拉着球头杆先运动，此时的拉力大小从0.5～1.4 N 逐渐增加；5.7～ 8.8 s，球头杆到达极限位置后推动球壳体一起转动，此时的拉力峰值为2.1 N；8.8 s时，新型双球面连接器转动到极限位置。实时拉力曲线与仿真的结果对比，看出连接器转动到极限位置的整个运动过程是相对应的。

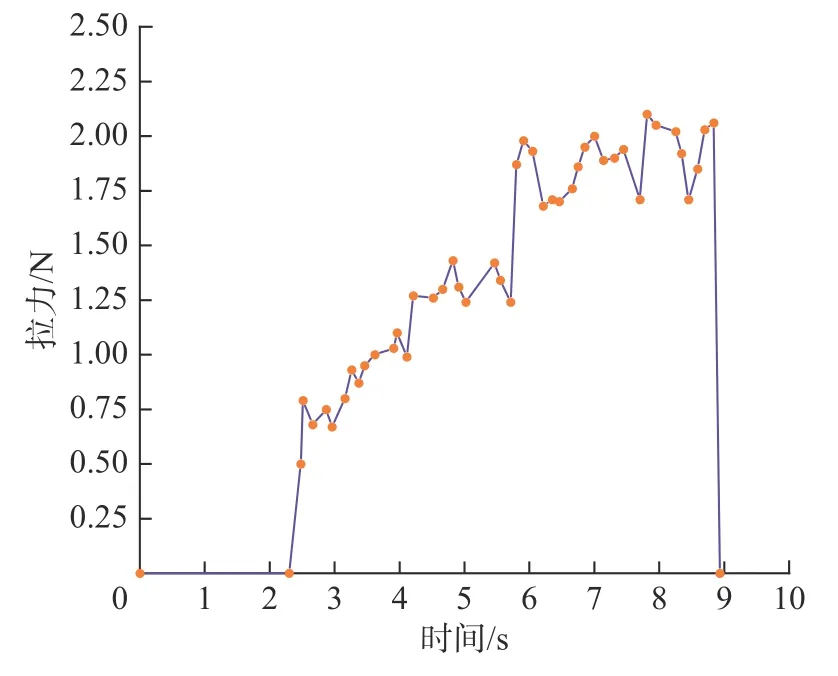
图10 实时拉力曲线

4 结论

1）新型双球面连接器具有内部走线通道，避免液压管线和电缆暴露在外部；设置限位销钉可以避免压瘪或剪断液压管线和电缆；任意方向上0～80°的偏转角度，提高机器人过弯能力；承受较大的轴向载荷，转动灵活，抗冲击性能好。

2）新型双球面连接器工作流程：球头杆先转动到极限位置后接触到球壳体，然后球头杆和球壳体共同转动到达极限位置。分析了轴向载荷为5 N、10 N 和15 N 这3 种不同工况下对转动角速度的影响规律。随着轴向载荷的增大转动角速度逐渐减小；随着轴向载荷的增大，所需要的转动力矩相应增加。

3）进行转弯实验，设计理论偏转角度为85°（中心线夹角105°），样机的实际偏转角度为80°（中心线夹角110°），由于加工和安装精度低，产生了5%的误差。转动实验所测的力矩与理论计算值接近。

4）由于连接器功能的独特性，可以促进管道智能封堵机器人这类管道内机器人连接零部件的多样化选择，提高这类的机器人完整性与安全性，促进相关机器人的发展。同样，本连接器球壳体和外壳体都是拆分的单个零件通过螺栓连接，对于转动力矩视情况而定，螺栓连接的松紧也会对转动力矩有影响，需要后续学者进行进一步研究。