一种可变径轮腿式越障机器人的设计与研究

丁冬冬，张守京

（1.西安工程大学 机电工程学院，西安 710048；2.西安市现代智能纺织装备重点实验室，西安 710600）

近年来，小型移动机器人在灾难救援、反恐、情报侦察等特殊任务中发挥了很好的作用，并且机器人可以代替人类在危险和狭窄的环境中执行搜救和排爆任务[1-3]。使用机器人代替人类好处颇多，不仅可以减少伤亡，而且效率也比较高[4]。现有的移动机器人主要分为轮式、履带式和仿生腿式[5-7]：轮式机器人在结构化的环境里可以快速高效地运行，但在非结构化的环境中适应性和越障能力较差；履带式机器人的优点是环境适应性好，并且其越障能力强，不足体现在速度和效率较低；仿生腿式机器人的优点是越障性能好，但结构和控制复杂[8]。显然，具有单一运动机构的移动机器人不能满足上述要求。因此，多运动混合式机器人成为研究热点。

目前，许多学者围绕机器人在非结构化地形中的稳定性和高越障性进行了大量研究。Jehanno 等[9]研制了六足轮腿混合移动机器人，它的每条腿上有5 个驱动关节，通过在每条腿的末端安装轮子，可以实现轮−腿混合运动。Ning 等[10]研制了一种四轮腿式移动救援机器人，该机器人主要应用于复杂的灾害现场，具有较高的承载能力和较强的越障能力等优点。Qiao 等[11]设计了一种具有活动腰部关节的轮腿机器人，通过在腰部增加可活动关节模块，使其可以在弯曲狭窄的通道中正常工作，且可以同时进行轮式和仿生足式的直线运动和转弯运动。Kim 等[12]研制了一种弯曲轮辐式三轮机构移动机器人，在轮与轮之间添加了止动机构，以此实现快速、稳定攀登楼梯的目的。Ryu 等[13]研制了一种用于高速攀爬的变形轮式机器人，其车轮可以通过在高速运动中的离心力使变形机构动作打开轮辐，使机器人可在非结构化地形中工作。张明路等[14]提出了一种轮-履复合被动自适应机器人，该机器人可进行正向和反向的越障工作，使其能在复杂的非结构化地形中正常工作。Torisaka 等[15]为了提高月球探测车的运行性能，提出了一种可以延长腿的车轮设计来增加驱动力，比较了车轮状态和腿部状态下的驱动力，结果表明，腿部状态比普通圆轮具有更大的驱动力。Sun 等[16]研制了一种可变形轮腿移动机器人，通过设计一种轮腿转换机构，将轮式的滚动和腿式的越障相结合，实现机器人既可应用于平坦的地形，也可应用于崎岖的地形。Ning 等[17]提出了一种具有较强环境适应性的轮腿救援机器人设计方案。该设计旨在帮助救援人员快速准确地完成环境和人员搜索等任务，实现了结构简单、易于控制、占用空间小、运动范围广的优点。魏军英等[18]研制了一种基于四杆机构的八轮式爬楼机器人，在一定程度上实现了机器人越障要求。以上文献研究发现，目前针对移动机器人在非结构化地形中的越障能力进行了不同程度的研究，无论是多运动混合机器人，还是开放的轮辐式机器人都在一定程度上增加了机器人对复杂非结构化环境的适应性和越障能力，但同时也造成运动效率低、运动稳定性差等问题。

基于上述问题，本文提出一种可变径轮腿式越障机器人设计方案，在变径机构的作用下车轮由轮式模式变换为轮腿式模式。使其同时具有轮式高效移动性和腿式较强的越障能力。

1 具有变径轮机构移动机器人的机械结构设计

1.1 变径轮结构设计

图1 是具有可变径轮腿式越障机器人的机械结构，它主要由两个具有变径机构的变径轮和矩形车身组成，采用左右对称布置的方式。通过变径机构实现轮式和轮腿式两种模式的转换，从而实现移动机器人的轮式纯滚动和轮腿式移动。矩形车身是为了搭载直流伺服电机和传动机构等其他硬件。变径机构设计如图2 所示。

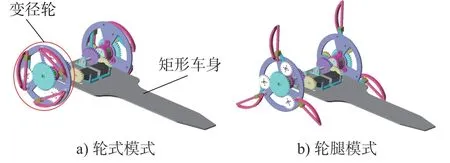
图1 具有变径轮机构的移动机器人3D 模型

图2 变径轮结构示意图

变径轮机构主要由以下几个部件组成：轮毂、电机、两个驱动齿轮、主轴、直流电机、滑块、3 个弧形腿、3 个曲柄和变形齿轮。如图2b）所示，为轮式模式，3 个弧形腿收缩在轮毂内，轮毂由主轴控制，通过接收直流伺服电机提供的动力，使机器人以恒定的速度运动。如图2c）所示，为轮腿式模式，由电机向变形齿轮提供动力，通过连杆使三个弧形腿向外展开，从而达到变径目的。同时为了增加车轮与地面之间的摩擦力，在弧形腿的弧面边缘上均匀的使其附着上橡胶。图2b）和图2c）中的r为轮式模式下车轮的半径，r′为轮腿式模式下弧形腿展开的最大半径。

综上所述，机器人在结构化的环境中，以轮式模式进行运动，此时直流伺服电机工作驱动机器人工作；在非结构化的道路上，机器人会以轮腿模式进行运动，此时直流伺服电机和电机同时工作，前者是为机器人提供前进的驱动力，后者是为变径机构的变形提供动力。这种简单紧凑的可变径结构使机器人可以自由切换工作模式，极大地提高了机器人的环境适应性。

1.2 变形比分析

变形比是可变形机构的一种设计参数[19]，是机构在发生变形后的半径和未发生变形时的半径的比值。变形比既能直接地反映变形机构变形能力的强弱和大小，又可以间接的反映其越障能力。本文所设计的变径轮的变形比为轮腿式模式时的半径r′与轮式模式时的半径r的比值。

在复杂路面上，机器人以轮式模式无法越过障碍，此时就由轮式模式变换为轮腿式模式，当其为轮式时的半径为r，为轮腿式时的半径为r′。

由结构设计可知，r=45 mm，r′=96.5 mm，则变形比为

通过计算可知，此变径机构具有较大的变形比，表明该机构可以为机器人提供较强的越障能力。

2 变径轮机构的分析

如图3 所示为变径机构运动简图，将该机构放置在笛卡尔坐标系中。以AB为原动件做转速为ω的匀速周转运动，且AB的长度为l1。杆OC为从动件，其运动规律为绕O点做摆动运动，且l2为其回转中心点O与原动件AB回转中心点A的中心距。滑块B为从动件，其运动规律不仅可以随着原动件AB做转动，而且还可以杆OC上做滑动。各个杆件的长度、相对位置以及原动件角速度ω均是已知的。图3 中的双点划线是变形齿轮，虚线是导杆OC的运动轨迹。变径机构工作时，原动件做圆周运动，带动弧形腿做展开和收缩运动，从而达到将圆轮转换为三辐条状进行越障的目的。

图3 变径机构运动简图

2.1 位移分析

由图3 可知，△ABO组成封闭矢量三角形，且矢量和为0，在ABOA封闭矢量环如为

建立投影到X、Y轴方向的位移方程如下：

式中：θ1、θ3、l3分别为曲柄AB的方位角，导杆OC的方位角，以及滑块B的运动行程。由式（3）计算可得：

2.2 速度分析

由式（5）可得该变径机构的速度方程为

2.3 加速度分析

由式（8）解得该变径机构的加速度方程

2.4 运动学仿真

在变径机构中，已知曲柄AB 的长度l1=27.5 mm，AO的长度l2=20 mm，原动件AB的方位角θ1沿顺时针转从初始位置90°至终点位置−250°，且角速度ω=10 rad/min。在SolidWorks 建立Motion 分析。

图4 为滑块在Motion 分析的结果曲线。由图4可知，变径轮机构从轮式模式变形为轮腿式模式仅用约2.7 s，图中所示的滑块运动特性曲线变化连续光滑，说明所设计的变径轮机构变形时比较平稳，有利于降低机构的冲击，可以提高变形时机器人的稳定性。

图4 滑块的位移、速度和加速度曲线

3 越障过程分析

越障机器人的越障能力主要由自身结构和外部地形环境等因素的影响。为验证变径机构的越障能力，对其两种不同的越障模式进行分析：当障碍物高度小于轮式模式半径r时，变径轮以轮式模式进行越障运动，可实现机器人快速高效运动；当所遇到的障碍物高度大于轮式模式半径r时，车轮通过变径机构变换为轮腿式模式，从而进行越障运动。对机构在两种不同模式下通过不同障碍物高度进行受力分析，从而得到机器人在不同模式下的极限越障高度。

3.1 轮式模式越障

当障碍物高度小于车轮半径r时，如图5 所示，机构以轮式模式进行越障运动，其运动性能可以通过对轮式模式下建立动力学模型分析得出。

图5 轮式模式越障受力分析

此时，轮式模式下的变径轮所受到的水平方向的力是由变径轮与地面的摩擦所产生的，该机构处于平衡状态，其力和力矩平衡式为：

式中：M为电机的转矩；G为自身的重力；FN1为地面的支持力；FN2为台阶接触处对弧形腿的支持力；f1为地面对弧形腿的摩擦力，f1=μFN1；f2为台阶接触处对弧形腿的摩擦力，f2=μFN2；α为台阶接触处的支持力与地面之间夹角，α=arcsin[(r−h)/r]，h为障碍物高度。

由几何关系可得

当α=0°时，轮式机构处于临界稳定状态，即FN1=0，除重力作用外，轮式模式不受水平外力，此时机器人在电机的驱动下，依靠其自身的旋转运动继续前进，可得轮式模式的最大越障高度，即

移动机器人以轮式模式进行运动时，当所需越障高度h小于轮式模式半径r时，则在电机的驱动下，依靠机器人自身的旋转运动可越障前进；当所需越障高度h等于轮式模式半径r时，则机器人需要在水平外力的帮助作用下才能顺利越障；当所需越障高度h大于轮式模式半径r时，则机器人不能越过障碍，此时机器人通过变径机构将轮式模式变换为轮腿式模式进行越障运动。

3.2 轮腿模式越障

在复杂非结构化的地形上，机器人通过变径机构使轮式模式变换为轮腿式模式进行越障。为研究机器人在越障过程中的受力情况，对轮腿式模式下的越障情况进行力学分析，各力的状态，如图6 所示。

图6 轮腿式模式越障受力分析

由力平衡条件得关系式如下：

式中：F1为重力对弧形腿的水平分力；F2为重力对弧形腿的竖直分力；f为台阶接触处对弧形腿的摩擦力；FN为台阶接触处对弧形腿的支持力；γ为台阶接触处的上平面与弧形腿的切线的夹角；μ为静滑动摩檫力因数；Mf为力f的力矩；MFN为力FN的力矩；T为动力系统驱动力矩。

当变径轮与台阶下表面接触的弧形腿1 即将脱离，且与台阶立面接触的弧形腿2 处于临界滑动状态时，此时弧形腿2 与立面接触点的摩擦力f和支持力FN存在的关系为

将式（15）代入式（14）中解得

若式（16）中，取临界值F1=0，轮腿的橡胶面与台阶面的静滑动摩擦因数μ=0.6，则

则由式（17）可得临界角，即

实际情况下，机器人在越障的整个过程中，其台阶接触处的上平面与弧形腿的切线的夹角 γ是不断发生变化的。当 γ ≤ 31°时，变径轮的弧形轮腿1 即将脱离接触台阶的下表面，这时可以利用弧形腿2 与接触台阶立面的摩擦力顺利翻越台阶；当 γ >31°时，变径轮的弧形轮腿1 支撑在接触台阶的下表面，此时依靠弧形腿2 的橡胶面纹理与接触台阶的立面棱角的抓力也可以使机器人顺利越障。

3.3 轮腿模式的最大越障高度

图7 为轮腿式模式下机器人的极限越障状态。

图7 极限越障状态

在图7 中存在的几何关系中，可以求出越障机器人的理论极限越障高度，即

式中l为弧形腿和台阶立面的切点与变径轮中点O的距离。

化简式（19）可得

由图7 可见，变径轮机构的其它部位不会与台阶立面发生接触，此时轮腿式模式在越障极限位置时的状态为，弧形腿1 与台阶立面和台阶地面相接触，弧形腿2 与台阶立面是相切关系，则根据其几何关系计算可得：

联立式（20）和式（21）求解可得

因此，变径轮机构的越障极限高度约为轮腿模式半径的1.72 倍。又由前文中所提出变径轮变形前后的的变形比为2.14，所以其越障高度约为轮式越障半径的3.69 倍。

4 变径机器人仿真分析

为测试越障机器人的稳定性和越障能力，运用ADAMS 软件对机器人在非结构化地形中进行仿真实验。在仿真环境中，添加弧形腿与地面的接触，并采用冲击函数模型，弧形腿与地面为库仑摩擦，具体的环境参数如表1 所示。

表1 环境参数

因为在非结构化地形中障碍物是具有多样性的，所以在仿真时将障碍物分为3 种情况：单台阶、连续台阶和复杂路面，分别进行仿真实验。

4.1 单台阶越障

单台阶越障如图8 所示，按照前文所叙述的情况本文将单台阶障碍物设计高度为最大（理论计算值），机器人处于极限越障状态，且将驱动电机的转速均设置为38 °/s，验证其越障性能的合理性及优越性。

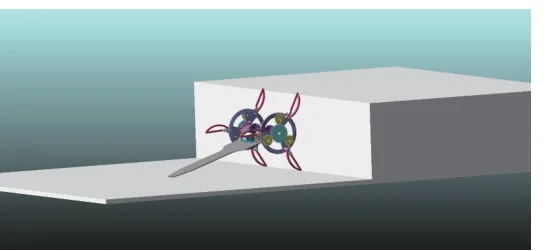
图8 单台阶越障仿真

仿真结果如图9 所示，在6.5 s 内机器人可以成功翻越理论计算值的台阶，机器人质心位移曲线表明在爬升过程中整体趋于稳定，且质心没有较大的波动，没有出现明显的卡顿；由机器人质心速度和加速的曲线可知，移动机器人在越障过程中整体速度保持在65 mm/s，加速度近似保持为0，在0.1 s 至3.2 s 速度为下降趋势，体现出此时变径轮正在翻越台阶，随后又恢复正常水平。在约3.4 s 时，速度与加速度均有一个突变，由此可以推断是由于弧形腿与台阶面产生了相对滑动。

图9 单台阶越障仿真位移、速度、加速度曲线

4.2 连续台阶越障

连续台阶越障如图10 所示，将驱动电机转速均设置为38 °/s，相似的，在ADAMS 的Postprocessor模块可以得到移动机器人在连续越障运动过程中的仿真数据。仿真结果如图11 所示，机器人质心位移曲线显示出近似为对称曲线，说明在81.5 s 内机器人可以成功上下连续台阶，且在上下台阶过程中整体趋于平稳，质心波动较小；由机器人质心速度和加速的曲线可知，移动机器人在上下连续台阶过程中整体速度保持约在65 mm/s，加速度几乎为0。在接近55 s时，速度与加速度均有一个明显的突变，由此可以推断在下台阶时弧形腿与台阶面会产生相对滑动。

图10 连续台阶越障仿真

图11 连续台阶越障仿真位移、速度、加速度曲线

4.3 复杂路面越障

机器人在复杂路面越障如图12 所示，驱动电机转速为38 °/s，同样的可以得到移动机器人在复杂路面越障运动过程的仿真数据。

图12 复杂路面越障仿真

仿真结果如图13 所示，由机器人质心位移曲线可知，在此工况下质心的位移与障碍物的高度大致吻合；由机器人质心速度和加速的曲线可知，移动机器人在穿越复杂路面过程中整体速度保持约65 mm/s，加速度接近为0。在大约55 s 前后，速度与加速度均有一处明显的突变，随后又迅速恢复到正常值，此时为机器人的弧形腿抬起后又迅速落到地面导致，与仿真中相符合。

图13 复杂路面越障仿真位移、速度、加速度曲线

由上述仿真实验可知，该具有变径轮机构的地面移动机器人对地形具有良好的适应性和较强的越障性，且结构合理、紧凑，具有良好的灵活性。

5 结论

1）本文提出了一种新型的具有变径机构的越障机器人方案，该机器人通过变径机构实现轮式和轮腿式两种工作模式的转换，与传统的机器人相比较，机构紧凑，自由度较少，便于控制。

2）对所设计的机器人在轮式和轮腿式两种模式下的越障性能进行了分析，得出在轮式模式下，当障碍物高度小于轮式半径式机器人可以依靠驱动电机顺利翻越障碍物，反之则通过变径机构使机器人转化为轮腿模式来越障，且最大越障高度可达到轮腿模式半径的1.72 倍，轮式越障半径的3.69 倍。

3）运用ADAMS 软件对该机器人在轮腿模式下翻越单台阶、上下连续台阶以及复杂地形的越障过程做了仿真分析，仿真结果与前文所述的理论计算值符合度较高，验证了具有变径机构的越障机器人方案的合理性，以及对不同地形有着良好的适应性和较强的越障能力。