年龄结构SI传染病模型行波解的有界性
李 竹,张天然
(西南大学 数学与统计学院,重庆 400715)
文献[1]研究了具有年龄结构的SI传染病反应扩散模型
(1)
其中,Π表示易感人群的输入率,γ表示死亡率,dS、dI分别表示易感人群和感染人群在空间中的扩散系数.除此之外,β(a)代表随年龄变化的感染概率,μ(a)表示由于疾病导致的死亡率.
本文假设下列条件成立:
(A1) Π、γ、dS和dI都是正常数;

定义基本再生数为
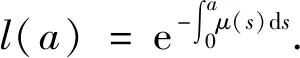
注意到,当R0>1时系统(1)有一个无病平衡点
和一个地方病平衡点
记α*>0是方程
λ2-cλ+α*=0
(2)
的最小根,此根必然是正的.
文献[1]证明了定理1.
定理1假设dS≥dI>0, 那么下面三条结论成立:
(ⅰ)如果R0≤1,那么系统(1)没有行波解;
(ⅱ)如果R0>1且c (ⅲ)如果R0>1, 那么对任意波速c>c*,系统(1)有一个行波解. 此外,如果行波解存在,则行波解在空间L1(0,∞)中满足 注意到定理1中对扩散系数添加了限制dS≥dI>0.文献[1]指出,对扩散系数的限制条件是为了保证证明过程中的行波解是有界的.如果此条件不成立,则文献[1]中的证明过程不再适用,从而无法得到定理1中的结论. 本文将引入新的方法证明定理1中的条件dS≥dI是多余的,去掉这个条件,定理结论仍然成立,从而使得定理更加完美. 系统(1)是非合作(或者非单调)的,因而单调动力系统的理论方法无法应用到此系统.近些年,对非合作反应扩散系统(包括传染病模型及捕食者-食饵模型)行波解存在性的研究获得了较大进展,主要方法有Schauder不动点定理[1-9]及几何方法(打靶法[10]).如果疾病发生率关于染病者是有界的或者捕食者相互作用项关于捕食者是有界的[3,7-8],则可以直接应用Schauder不动点定理得到行波解的存在性和有界性;如果疾病发生率是线性的或捕食者功能反应是HollingⅠ~Ⅲ类型,则行波解的有界性问题不易解决.文献[4-5]用Rescaling方法解决了此种行波解的有界性问题,而文献[10]使用几何方法得到了行波解的有界性.由于系统(1)带有年龄结构,则生成的动力系统是无穷维的,故文献[10]中的方法无法直接应用到模型(1);由于同样的原因,文献[4-5]使用的Rescaling方法也无法直接应用到本文的模型.本文将克服年龄结构所带来的困难,创造性地发展文献[1,4-5]中的方法以解决模型(1)行波解的有界性问题. 假设(A1)和(A2)总是成立的,则本文的主要结论如下: 定理2下面三条结论成立: (ⅰ)如果R0≤1,那么系统(1)没有行波解; (ⅱ)如果R0>1且c (ⅲ)如果R0>1,那么对任意波速c>c*,系统(1)有一个行波解. 此外,如果行波解存在,则行波解在空间L1(0,∞)中满足 在定理2中,去掉了原定理1的限制条件dS≥dI>0, 结论保持不变.因此,定理2的适用范围更广.为了说明我们的证明方法,下面先把文献[1]中已有的定理叙述出来,然后再说明我们进一步的处理步骤. 根据文献[1]第二节中的内容可知,经过适当的变量变换,总可以假设 dI=1,Π=γ,μ=0 (3) 成立.在此假设下,为了研究模型(1)的行波解的存在性,只需研究如下系统 (4) 假设式(3)成立,此时无病平衡点和地方病平衡点变为 SF=1,iF=0 为了后续证明的需要,把文献[1]中的命题2.5叙述为 引理1假设式(3)成立,则系统(4)有解 且满足 0 (5) 注释1由文献[1-2]的证明过程可知,解(S,i)是古典解. 由文献[1]的证明可知,条件dS≥1=dI只被用来保证文献[1]中的引理2.6成立.因此,本文需证明在没有限制条件dS≥1=dI的情形下,引理2.6的结论仍然成立.去掉限制条件dS≥1=dI的引理2.6叙述如下: 引理2假设式(3)成立,则引理1的解(S,i)满足 (a)存在常数M>0,使得对任意的a≥0和x∈R,有i(a,x)≤Me-γa; (b)存在常数ε0,使得infRS>ε0. 为了完成引理1的证明,只需证明引理2即可. 证明引理2(a)定义 将模型(4)关于变量a在区间(0,∞)上积分得 (6) 步骤1如果存在xn→+∞,使得I(xn)→+∞,则在Cloc(R)中S(x+xn)→0,即S(x+xn)在x∈R上局部一致收敛到零. 由Harnack不等式(见文献[4]中的引理2.1)可知,n→∞时, 其中,L是固定的正常数. 由假设(A2)可知,对任意的x∈R有 从而有 (7) 结合式(7)易知,当n充分大时, 令ω(x)=U(x)-S(x+xn),则有ω(±l)≥0.进而 步骤2不可能存在xn→∞,使得 I(xn)→+∞,I″(xn)≤0 (8) 用反证法,假设式(8)成立.令 则In(0)=1,且有 (9) 由假设(A2), V″(x)-cV′(x)-γV=0 (10) 的非负解,这里用到了步骤1的结论.由非负性可得 V(x)=a1eλ1x+a2eλ2x 其中,a1≥0,a2≥0,a1+a2=1,且λ1<0<λ2是特征方程λ2-cλ-γ=0的两个根.由于 从而当n充分大时 与假设矛盾. 步骤3对充分大的x≫1,I(x)是单调递增的,且x→∞时,有I(x)→∞.此结论可由步骤2的结果直接推出来. 任取序列xn→∞,令 由步骤2证明可知In(x)→V(x),其中,V(x)=a1eλ1x+a2eλ2x,且a1、a2、λ1、λ2满足步骤2中的条件. 步骤3说明对充分大的x≫1,I(x)是单调递增的,故a1=0,a2=1,V(x)=eλ2x.由序列xn的任意性,存在M1>0,使得对充分大的x有 注意到λ是方程(2)的最小根,因此λ<λ2. 由定理2可知 当x足够大时得出矛盾.由此,已经证明了I(x)在R上有界.记M3=supRI(x). 下面进一步完成引理2(a)的证明. 注意到i是下面问题的解 由文献[1]中的引理2.7知 是椭圆算子∂xx-c∂x-γ的Green函数.进而i可以表示为 Me-γa 和 引理2(a) 证明完成. 因为S*(0)=0=S*′(0),S*″(0)≥0,所以γ=0,这与γ的定义矛盾,假设不成立.证毕. 本文运用Rescaling方法和比较原理得到了行波解的有界性.相较于文献[1]中的证明,本文不仅去掉了对扩散系数的限制,并且证明过程更加简洁易懂.阅读文献[1]中的其他定理,对带年龄结构的传染病模型行波解相关性质的认识将会更加清晰.1 主要结论及证明
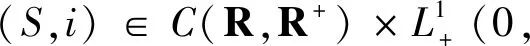




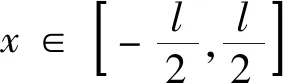


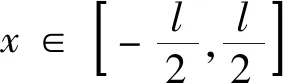
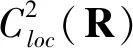


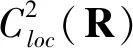

2 结语

