资源有限下具有抗药性发展的害虫综合治理切换模型研究

金佳妮,齐加齐,刘 兵

(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

害虫是农业生产的主要危害之一.化学控制和生物控制是最常用的害虫控制方法,在实际应用中,通常将两种控制策略结合起来综合治理害虫.国内外很多学者利用数学模型研究害虫控制问题:有学者假设杀虫剂瞬时成比例杀死害虫[1-3],实际上,杀虫剂的作用并不是瞬时完成的,而是具有一定的残留及滞后效应;也有学者引入杀虫剂作用函数来模拟杀虫剂产生的残留与滞后效应[4-5].文献[1-5]中均假设天敌投放量为常数.事实上,由于天敌资源的有限性,天敌的投放量需要依赖现有天敌的数量,非线性地释放天敌[6].考虑多次重复使用同一种杀虫剂将导致害虫对杀虫剂产生抗药性,学者们进一步研究了具有抗药性发展的害虫综合治理模型[7-8].基于上述研究背景,本文建立并研究一类资源有限下具有抗药性发展的害虫综合治理切换模型.

1 模型的建立

本文考虑资源有限条件下天敌的投放量依赖于现有天敌的数量,假设在每个年度周期内,只在害虫爆发的时间内使用杀虫剂,在使用杀虫剂和不使用杀虫剂的不同时段,天敌对害虫的捕食率函数、转化率不同,考虑杀虫剂的残留作用,建立资源有限的害虫综合治理切换模型

(1)

bi(t)=mie-δi(t-(n+l)T-kTp),(n+l)T+kTp≤t≤(n+l)T+(k+1)Tp,k=1,2,…,p

其中,mi>0(i=1,2)分别表示杀虫剂对害虫和天敌的非瞬时杀死率,δi>0(i=1,2)分别表示杀虫剂对害虫和天敌的衰减率.

本文将害虫种群分为两类:一类是对杀虫剂敏感的害虫xs(t),另一类是对杀虫剂具有抗药性的害虫xr(t).设在t时刻敏感害虫xs(t)的比例为q(t),即

则抗药性害虫xr(t)的比例为1-q(t).设初始时间敏感害虫的比例为q(0)=q0,并且假设不喷洒杀虫剂时,即t∈(nT,(n+l)T]时,害虫的抗药性不发展.

因此,当t∈((n+l)T,(n+1)T]时,敏感害虫xs(t)和抗药性害虫xr(t)分别满足方程

这样,当t∈((n+l)T,(n+1)T]时,害虫种群增长模型就变为

通过计算,得到

(2)

所以,可以得到资源有限下具有抗药性发展的害虫综合治理切换模型

(3)

其中,q(t)满足式(2).

通过计算,q(t)在任意区间(nT,(n+1)T](n∈N)的解析解为

(4)

其中,

2 害虫灭绝阈值的分析

首先,考虑系统(3)的子系统

(5)

可以得到如下定理:

定理1如果θ≠0,子系统(5)有一个全局渐近稳定的周期解

(6)

其中,

证明通过对系统(5)中的方程进行积分,并将所得到的式子进行迭代计算,可得

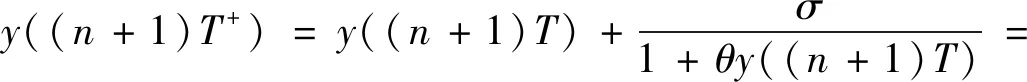
令

Yn=y(nT+)

有

(7)

当θ≠0时,方程(7)有唯一的正不动点

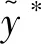
那么

同时

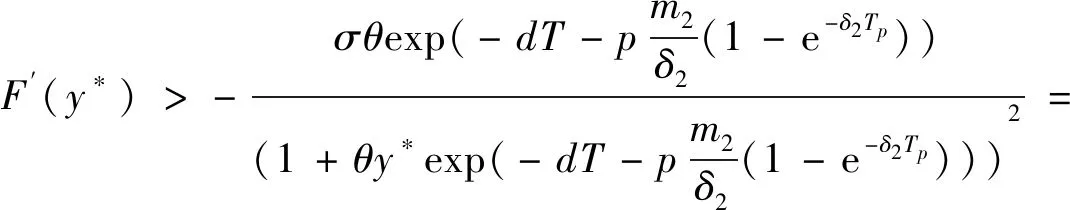
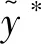
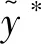
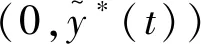
证明因为Rn<1,所以存在充分小的ε,且ε>0,使得

由于t∈(nT,(n+1)T]时,

因此, 当t→∞时,x(t)→K+ε.

又由系统(3)可得

考虑如下脉冲微分方程

为方便起见,不妨假设上式对所有t≥0均成立,则有

由脉冲微分方程比较定理,当t∈(nT,(n+1)T]时,有

x(nT+)χ

x(nT+)≤x(0+)χn

由于χ<1,进而,当n→∞时,x(nT+)→0,因此,当t→∞时,x(t)→0

对于两个不等式的左端由脉冲微分方程比较定理可得,当y(t)≥N(t),且t→∞时,N(t)→y*(t).对于上面两个不等式的右端,考虑如下脉冲微分方程

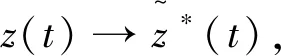
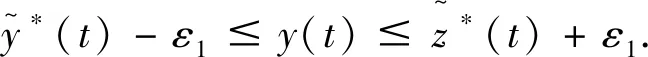
3 数值模拟与结论

本文研究了一类资源有限下具有抗药性发展的害虫综合治理切换模型,通过理论分析得出害虫灭绝的阈值,证明了害虫灭绝周期解是全局吸引的.下面通过数值模拟研究模型中关键参数对害虫灭绝阈值的影响.

由定理2可知,害虫灭绝的阈值依赖于许多参数,将其中的参数取值为r=0.5,K=10,α1=0.2,α2=0.25,d=0.05,m2=0.25,σ=10,θ=15,δ1=0.1,δ2=0.25,q0=0.99,l=0.1,p=2,ω=2,x0=8,y0=5,c1=0.1,c2=0.1, 其他参数如图1、图2所示.

图1 T=2时Rn随着n的变化趋势图 图2 T=2,m1=0.6时害虫、天敌的时间序列图

图1模拟了杀虫剂对害虫的非瞬时杀死率m1取不同数值的情况,控制策略次数n对害虫灭绝阈值Rn的影响.可以看出,Rn是关于n的递增函数.当施行控制次数较少时,害虫没有产生抗药性,此时杀虫剂对害虫的非瞬时杀死率m1越大,杀虫剂对害虫起的作用越强.但是,随着施行控制次数的增多,害虫的抗药性逐渐发展,并且m1越大,抗药性发展得越快,最终Rn的值将大于1,即害虫最终会爆发(见图2).

研究发现,多次喷洒同一种杀虫剂会使害虫产生抗药性,并导致害虫种群爆发.因此,在以后的研究中,可以讨论如何切换杀虫剂或弹性释放天敌来控制害虫.