双腔室自振脉冲喷嘴空化射流数值模拟
于海涛, 徐艳, 刘海水, 王佳祥
(东北石油大学 机械科学与工程学院,黑龙江大庆 163318)
空化是指当流体内的压力低于其饱和蒸气压时,流体中的空化核析出、发展、溃灭的过程。由于空化核在溃灭过程能对固体表面产生强大的破坏作用,因此,Johnson等[1]提出将空化与水射流技术结合产生空化水射流能极大提高射流的冲蚀能力。空化水射流技术在石油钻井、清洗除锈、金属喷丸等领域有着广泛应用[2-5]。Yang等[6]利用高速摄像研究了角形空化喷嘴的扩散角对空化云的非定常流动特性的影响,并对靶面的冲蚀机理进行分析。Liu等[7]实验研究了倾斜表面上空化射流的冲蚀及其自激振荡行为,分析了冲蚀形貌与射流振荡频率随角度的变化规律。张坤等[8]对自激脉冲喷嘴采用4种湍流模型进行数值计算对比,并分析了谐振腔一个振荡周期内空化初生、发展的演变过程。Fujisawa等[9]采用高速摄像对空化云的溃灭形态进行观测,并对靶面冲蚀坑深度及数量进行了分析。王萍辉等[10]对射流振动信号进行分析,研究了喷嘴自激振动频率特性,得到了实验工况下最佳喷嘴结构。李根生等[11]利用水声学原理和瞬态流理论对风琴管喷嘴的工作原理进行分析,得到了谐振腔结构的基本设计模式。戚美等[12]对双腔室自振空化喷嘴的内流场进行仿真计算,分析了来流雷诺数、腔长比和腔径比对空化流场的影响。邓嵘等[13]利用Fluent优化了双腔室自振喷嘴的二级谐振腔结构,并与单腔室自振空化喷嘴的射流打击力进行了对比分析。为了提高喷嘴的空化射流能力,相关学者对单腔室喷嘴的射流机理、结构尺寸等方面做了大量研究,但对双腔室自振空化射流喷嘴的相关研究较少。因此,本文基于风琴管喷嘴串联一个二级谐振腔形成双腔室自振空化喷嘴,利用fluent对其内外流场展开研究,分析谐振腔的腔长比、腔径比和射流靶距对空化射流效果的影响,旨在提高喷嘴的清洗效率。
1 计算模型
1.1 物理模型
根据蔡腾飞等[14]和唐川林等[15]研究的喷嘴结构为主,建立的双腔室自振脉冲喷嘴由风琴管喷嘴与二级谐振腔两部分构成,其结构尺寸如图1所示。
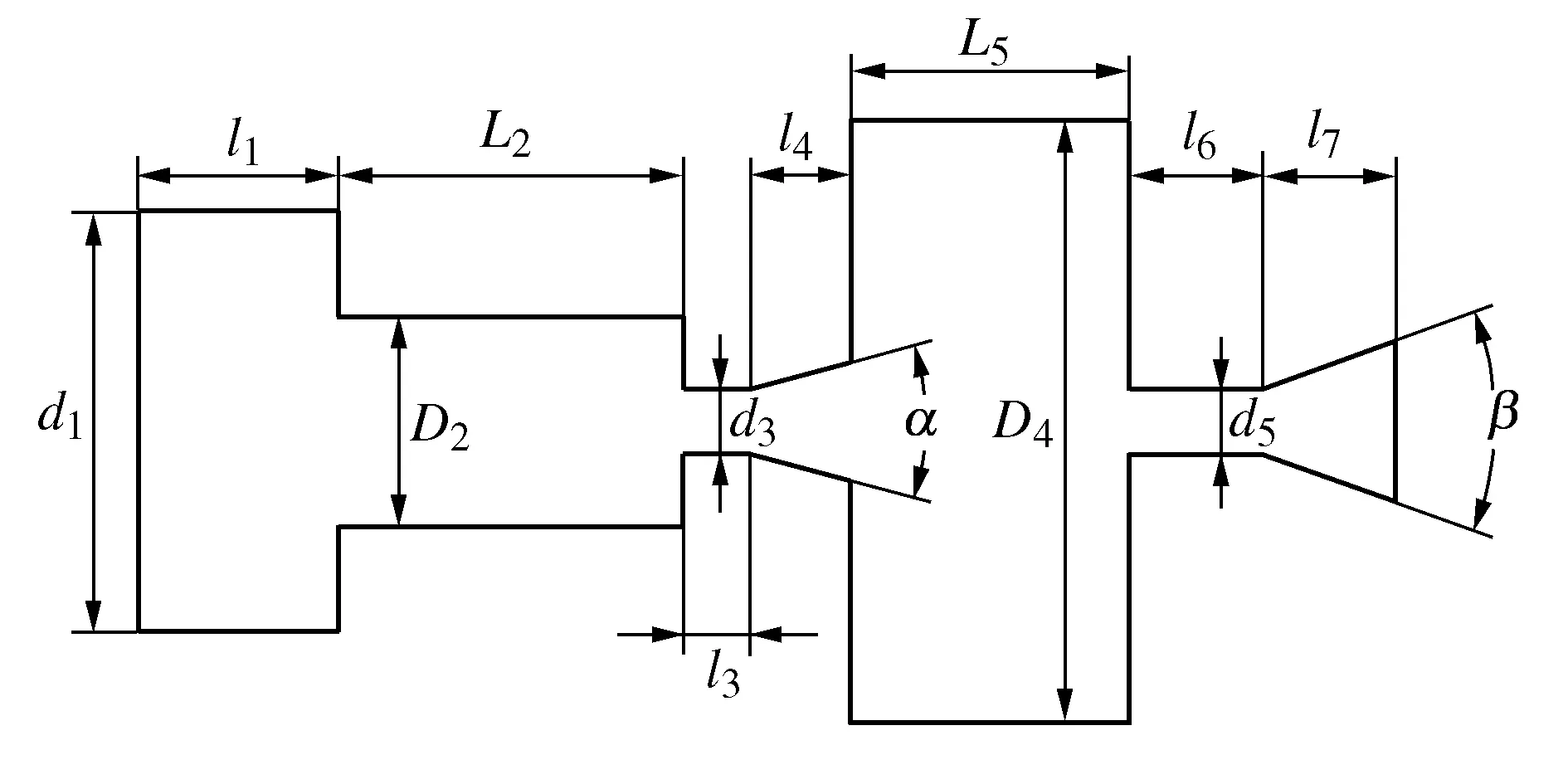
图1 喷嘴二维示意图
双腔室喷嘴中风琴管喷嘴段尺寸:入口腔直径d1=6.4 mm,谐振腔直径D2=3.2 mm,圆柱段直径d3=1 mm,入口腔长l1=3 mm,谐振腔长L2=5.2 mm,圆柱段长l3=1 mm,扩散段长l4=1.5 mm,扩散角α=30°。二级谐振腔段尺寸:谐振腔长L5=4 mm,谐振腔直径D4=8.4 mm,出口圆柱段直径d5=1 mm,圆柱段长l6=2 mm,扩散段长l7=2 mm,扩散角β=40°。来流经风琴管喷嘴谐振腔产生自激振荡后进入二级谐振腔,在二级谐振腔的作用下射流自激振荡得到加强,使空化射流效果得到进一步提高。
1.2 数学模型
时均后的Navier-Stokes方程如下:
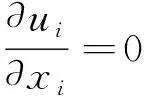
(1)
(3)
式中:ui、uj、p略去平均号“-”,表示平均速度分量、平均压力;μ为流体动力黏度;ρ为流体密度;τij为雷诺应力,需要对其建立湍流模型对方程进行封闭。
RNGk-ε模型输运方程:
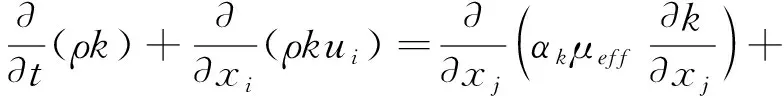
Gk+Gb-ρε-YM+Sk
(4)
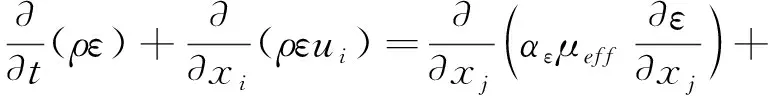
(5)
式中:Gk为速度梯度产生的湍动能项;Gb为浮力产生的湍动能项;YM为湍流脉动膨胀对总耗散率的贡献项;αk、αε为湍流Prandtl数;C1ε、C2ε、C3ε为常数项;Sk、Sε为自定义源项。
Schnerr-Sauer空化模型[16]为
(6)
式中:α为汽相体积分数;ρv为汽相密度;ρl为液相密度;ρ为混合相密度;vv为汽相速度。
1.3 网格的划分与边界条件的设定
对计算域采用ICEM进行网格划分。为了提高计算精度,对网格局部加密,并进行网格无关性分析,当网格数为45 176时可满足计算要求。由于喷嘴计算域为轴对称结构,取二维模型的一半进行数值计算。在距离喷嘴出口20 mm处设置射流冲击靶面。喷嘴的网格划分如图2所示。
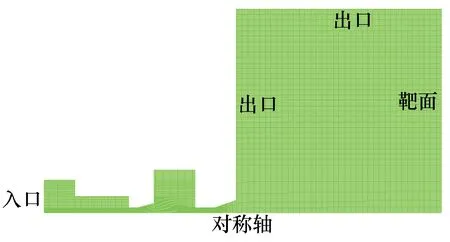
图2 计算域网格划分
喷嘴入口条件设为pressure-inlet,压力值设为20 MPa。喷嘴出口条件设为 pressure-outlet, 压力值设为101.325 kPa。求解器采用压力速度耦合算法,采用2阶迎风离散格式,用壁面函数法对近壁区处理。
2 计算结果分析
2.1 谐振腔腔长比对空化流场的影响
谐振腔尺寸会对射流自激振荡产生显著影响,进而改变空化射流效果。本文定义谐振腔腔长比为X=L5/L2,通过改变L5,腔长比X分别取0.58,0.77,0.96,1.15得到图3所示流线图。
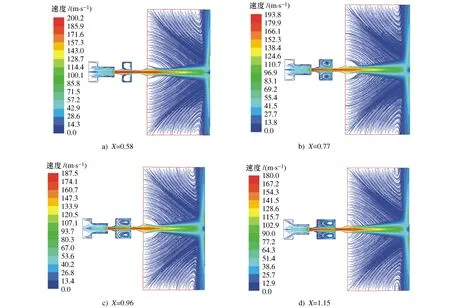
图3 腔长比X不同时的流线图
由图3可知,当腔长比为0.58时,二级谐振腔内无明显涡环结构产生。当腔长比增加到0.77时开始出现明显的涡环结构流线,且对称性较好。随着腔长比X增加,过大的腔长比减弱了谐振腔碰撞壁对射流的反馈作用,降低了自激振荡效果,导致涡环结构对称性变差。涡环结构对称性变差使射流剪切及压力分布受到影响,进而影响到能量的耗散及空化核的发育。图中可见,不同腔长比喷嘴其最高射流速度分别为200.2 m/s,193.8 m/s,187.5 m/s,180 m/s,随着腔长比增加,射流速度降低,这是因为随着谐振腔长度增加,涡环结构对称性变差,射流能量耗散增大引起的。
图4为不同腔长比喷嘴其轴向含气率分布曲线图。
图4中横坐标是以喷嘴入口为原点的轴向位置坐标。图中可见,当腔长比为0.58时,轴向含气率峰值远低于其他喷嘴结构。结合图3可见,这是因为二级谐振腔尺寸过小无法产生有效的自激振荡,使来自一级谐振腔的射流无法得到进一步加强,因此空化效果较差。因二级谐振腔无法产生自激振荡,射流高速穿过二级谐振腔时产生负压,使得二级谐振腔处产生了空化,因此在轴向10 mm处出现气相分布。当腔长比为0.77时含气率最高,随着腔长比增加含气率下降,这是因为随着腔长比增加,涡环结构对称性变差,对射流的增强作用减弱,进而影响到气相的生成。由上述分析可知,当腔长比为0.77时,射流流速较高,涡环结构对称性好,含气率高,因此对腔长比为0.77的喷嘴展开进一步研究。
2.2 谐振腔腔径比对空化流场的影响
以腔长比为0.77的喷嘴作为研究对象,定义腔径比Y=D4/D2,改变D4,腔径比Y取2.0、2.6、3.2、3.8的流线分布如图5所示。
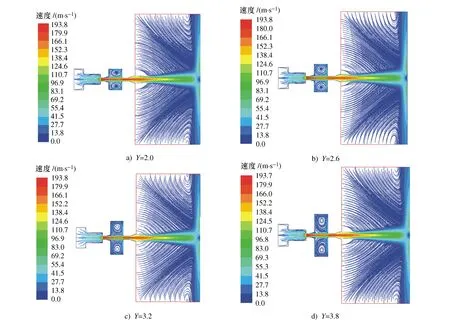
图5 腔径比Y不同时的流线图
由图5可见,当腔径比为2.6时涡环结构对称性最佳,继续增加腔径比,涡环结构对称性变差。
图6为喷嘴轴向含气率分布曲线图。图6中可见当腔径比为2.6时轴向含气率最高,可产生较好的空化射流效果。继续增加腔径比含气率下降。综上,当二级谐振腔腔长比为0.77,腔径比为2.6时,谐振腔涡环结构对称性好,射流速度较高,轴向含气率高,可产生较好的空化射流效果,有利于射流清洗效率的提高。
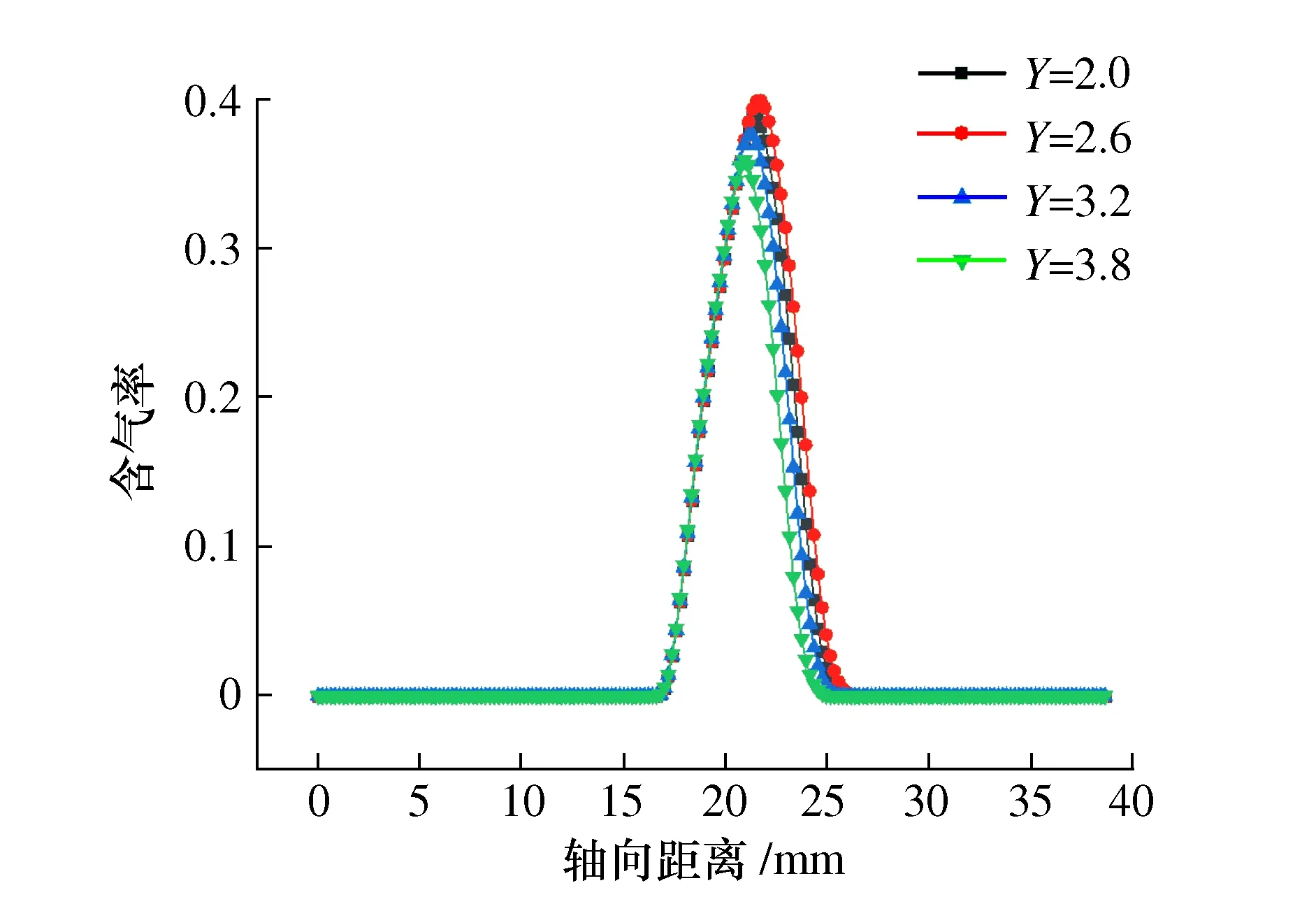
图6 喷嘴轴向含气率分布图
2.3 靶距对空化流场的影响
对二级谐振腔腔长比为0.77,腔径比为2.6的喷嘴,其射流靶距分别取10 mm、15 mm、18 mm、20 mm,观察射流靶距对空化效果的影响。
由图7可见,当靶距为10 mm、15 mm时二级谐振腔未产生涡环结构,当靶距增加到18 mm、20 mm时涡环结构出现,说明靶距会对二级谐振腔的内流场产生影响。
图8是以喷嘴入口为原点的轴向含气率分布曲线图,当射流靶距取10 mm、15 mm、18 mm、20 mm时,靶面位置坐标分别为28.7 mm、 33.7 mm、 36.7 mm、 38.7 mm。
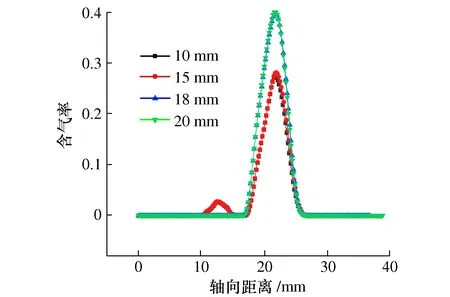
图8 喷嘴轴向含气率分布图
由图8可见,当靶距为10 mm、15 mm时,含气率较低,且在二级谐振腔附近(大于10 mm处)出现气相分布,结合图10可知,这是因为二级谐振腔未产生有效的自激振荡,射流高速穿过二级谐振腔时产生负压导致空化的产生。当靶距增加到18 mm时,含气率明显提高,且二级谐振腔处气相分布消失,这是因为在该靶距下二级谐振腔产生了自激振荡,使来自一级谐振腔的射流振荡得到加强,提高了空化射流效果。继续增加靶距至20 mm,含气率无明显变化。
图9为冲击靶面的滞止压力分布曲线图,其中,横坐标是以靶面中点为坐标原点,压力沿靶面垂直方向分布,靶面顶端坐标为20 mm。
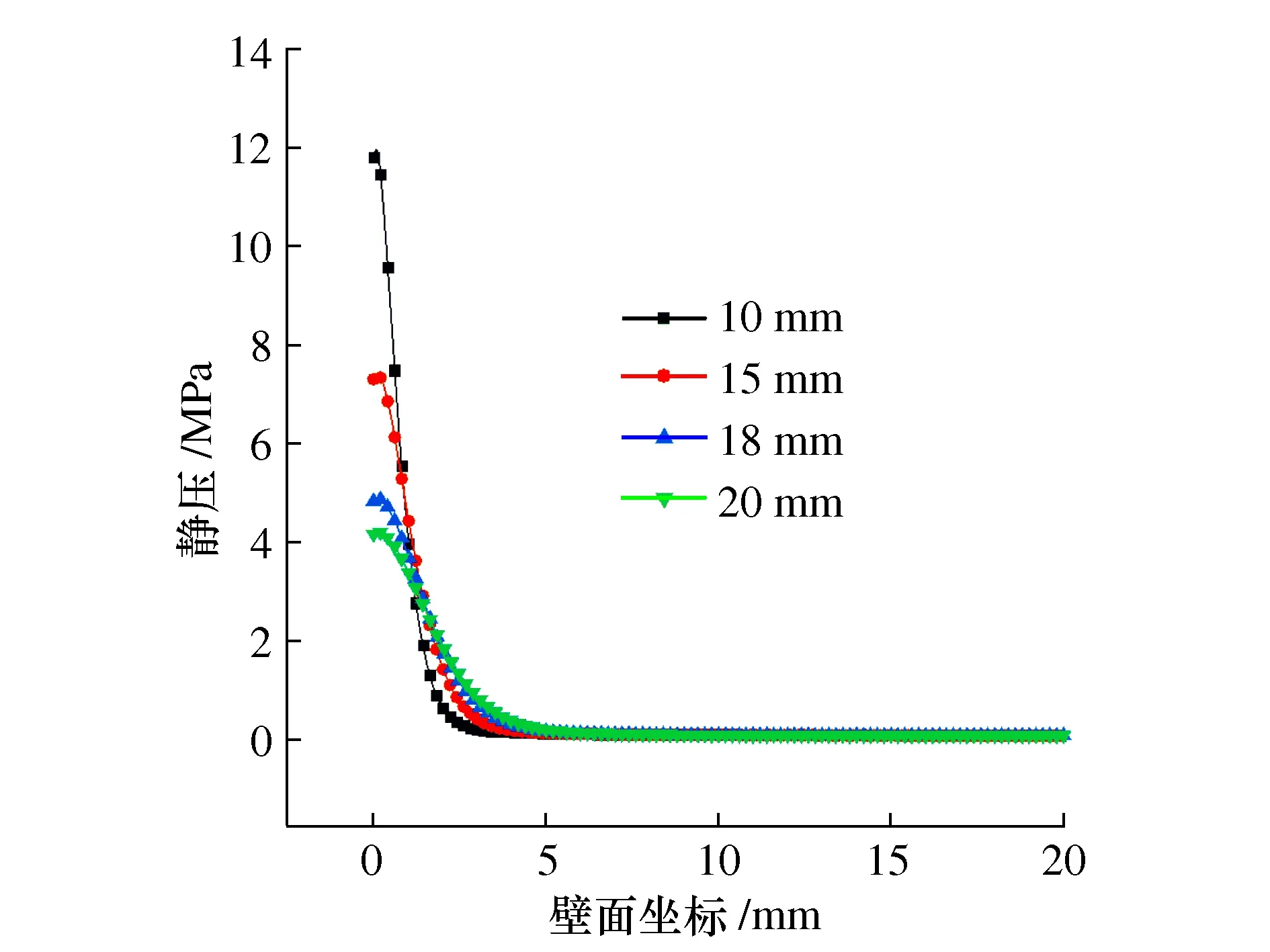
图9 壁面滞止压力分布图
图10为不同靶距下的静压分布云图,为了观察滞止压力对空化作用的影响,将所显示的最高压力设置为1 MPa。由图10中可见,靶面滞止压力能对轴向静压产生较大影响。结合图9可见,随着靶距减小靶面中心滞止压力迅速升高,当靶距从18 mm减小至15 mm时,滞止压力约有2.1 MPa的升高,由此可知,当靶距从18 mm减小至15 mm时,靶面产生的滞止压力过高,抑制了二级谐振腔涡环结构的产生,从而导致含气率降低。图中可见,随着靶距增加,靶面滞止压力梯度降低,分布范围增加。综上可知,射流靶距应至少18 mm才可产生较好的空化射流效果,但靶距的增加会降低射流到达靶面的动能,因此最佳清洗靶距应取18 mm。
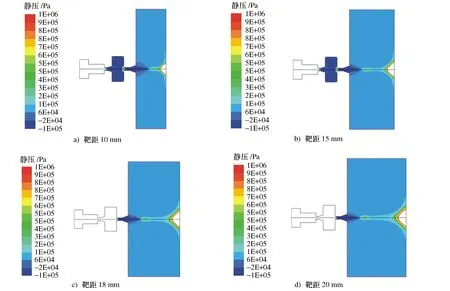
图10 不同靶距的静压分布云图
3 结论
1) 将双腔室喷嘴二级谐振腔腔长比分别取0.58、0.77、0.96、1.15的数值计算结果表明,当腔长比为0.77时,二级谐振腔内涡环结构对称性较好,射流速度较高,轴向含气率高,利于增强空化效果。
2) 以腔长比为0.77的喷嘴为研究对象,腔径比分别取2、2.6、3.2、3.8的计算结果表明,当腔径比为2.6时,二级谐振腔内的涡环结构对称性最好,轴向含气率高,该喷嘴结构可产生较好的射流清洗效果。
3) 射流冲击靶面产生的滞止压力随靶距的减小而迅速升高。当靶距较小时,在靶面滞止压力的作用下二级谐振腔的自激振荡受到抑制,进而影响到气相的生成。当靶距达到18 mm时,滞止压力大幅降低,对谐振腔的影响减弱,射流含气率提高。因此,为减少靶面滞止压力对空化效果的影响,射流靶距应至少取18 mm。但随着靶距的提高射流到达靶面的动能会降低,因此最佳清洗靶距应取18 mm。

