利用聚类分析的宏细观多尺度并行拓扑优化设计方法研究

舒定真, 郭伟超, 苏力争, 任鹏飞, 刘永, 李言

(1. 西安理工大学 机械与精密仪器工程学院,西安 710048;2. 西安电子工程研究所,西安 710100)

结构拓扑优化是用来寻找给定设计域最优结构材料分布的一种方法,被广泛应用在航空航天[1-2]、汽车[3-4]、医学[5]等领域。近年来已开发出许多不同的拓扑优化方法,例如均匀化方法、变密度法、进化结构法、水平集法等[6]。随着现代工业产品对结构性能要求的日益提升,传统拓扑优化已无法满足这样的需求。由微结构组成的多孔结构具有出色结构性能的同时结构质量更轻,例如具有更高的比刚度和比强度[7-8],更好的能量吸收率[9-10],更强的热传导能力[11-12]等性能。传统的蜂窝夹层结构由于其制造简单,已在航空航天、汽车、船舶等领域得到广泛的应用[13-15]。增材制造(Additive manufacturing, AM)技术的出现极大的增加了结构设计、制造方面的自由度,具有复杂构型的多孔结构制造已不再是难题。使用拓扑优化的方法可以对微结构进行设计,得到性能优异的多孔结构。

考虑微结构的拓扑优化方法主要可以分为单尺度拓扑优化与多尺度拓扑优化。单尺度拓扑优化只考虑微结构的性能,从而得到具有特定性能的微结构,例如设计具有负泊松比[16]、最大体积/剪切模量[17]、特定热传导率[18]等性能的微结构。这种方法主要集中在材料的细观结构设计上,为了追求性能更高的结构,应同时考虑材料的细观结构及宏观边界条件,因此多尺度拓扑优化的需求变的越来越强烈。

从结构性能最大化的角度上看,应该对每个微结构进行设计,但这样设计变量的数目就会变的十分庞大,计算成本令人难以接受[19-20]。为了将计算量降到可接受的程度,同时又得到整体性能较好的结构,目前大多数多尺度拓扑优化方法是假设宏观结构被划分为有限个区域,同一区域具有相同的微结构,以此实现结构性能与计算效率并重的目的。Gao等[21-22]基于水平集的方法研究了具有多区域微结构的多尺度拓扑优化,采用自由材料分布的优化方法得到不同微结构的区域来限制微结构的位置,再采用并行优化得到微结构的构型和分布。杜义贤等[23]研究了具有吸能和承载特性的多尺度优化结构,采用聚类的方法划分宏观区域,再根据聚类后的结果进行了微结构设计。Liu等[24]采用基于聚类的优化方法进行了防撞结构设计,通过模型全局优化、聚类、微结构设计等步骤对2维和3维结构进行优化设计验证了方法的有效性。Kumar等[25]提出K均值聚类的微结构拓扑优化方法,在优化流程上使用非并行多尺度优化,首先对宏观结构进行拓扑优化,根据宏观优化结果使用聚类方法划分微结构的区域,之后对每个区域内的微结构进行优化分析,同时通过引入转动自由度解决了微结构之间的连接性问题,得到连接性能良好的结构。

目前采用聚类的多尺度拓扑优化方法没有考虑微结构构型对宏观聚类结果的影响,微结构构型优化与宏观优化是分开进行的,属于非并行的优化。本文提出了一种新的基于聚类方法的多尺度并行拓扑优化方法,针对宏观优化结果,采用聚类的方法进行微结构区域划分,得到微结构的体积及宏观位置分布;再进行细观的微结构拓扑优化,得到微结构的构型;之后将优化结果反映在宏观上,指导下一步的宏观优化,依次循环,直到得到最佳微结构构型及位置分布。这种方法根据每步优化的结果及时更新微结构的位置及体积,增加了设计的自由度。

1 利用聚类分析的多尺度并行拓扑优化模型

多尺度拓扑优化需要根据宏观的优化结果指导细观微结构优化的进行。变密度法能产生丰富的中间密度单元,以中间密度单元作为微结构的体积约束,可以十分便利的进行多尺度优化,因此本文选取变密度法作为多尺度并行优化方法。固体各向同性材料惩罚模型(Solid isotropic material with penalization model, SIMP)是变密度法的最常用模型,主要原理是通过引入惩罚因子,建立单元相对密度与材料属性之间的显示表达式,其作用是对相对密度在(0,1)之间的单元进行惩罚,使其向0或1靠近,即

(1)

式中:E0为单元相对密度为1时的弹性模量;Ei为单元i的弹性模量;xi为单元i的密度;p为惩罚因子。当p>1时对单元有惩罚的作用,当p=1时对单元无惩罚作用。为了产生丰富的中间密度单元来设计微结构,宏观优化的p=1,一般的,细观微结构优化的p≥3。

在给定优化设计模型的前提下,以结构最大化刚度(柔度最小)作为设计目标,建立并行设计的宏观优化及细观微结构优化的数学模型为:

j=1,2,…,Nm)

(2)

宏观优化的惩罚因子为pM=1得到数量众多的中间密度单元,为减少设计变量提升计算效率,需将密度划分为数个区域,同一区域密度值相同。在多尺度优化中,其设计变量数目为(NM+NMNm)。采用聚类策略,将多个宏观单元映射到同一个微结构,共享同一组设计变量,其设计变量数目减少为(NM+θNm),由此可见聚类方法可以有效地提升多尺度优化计算效率。

常用的聚类方法有模糊C均值聚类、K均值聚类、层次聚类等方法。在对宏观优化结果进行划分时,采用模糊C均值聚类法得到的结果较稳定,故本文采用模糊C均值聚类法对结构进行聚类分析。

在对宏观单元进行区域划分时,可以采用均匀密度划分方法将0-1分布的密度分为θ等份,也可以采用聚类策略将宏观单元密度分为θ区域。如图1a)所示为宏观优化结果,对宏观优化结果进行均匀密度划分。

图1 宏观单元密度划分

将0～1之间的密度均匀的分为5类,当单元密度属于[0,0.2)时,假定单元密度为0.1;当单元密度属于[0.2,0.4)时,假定单元密度为0.3;当单元密度属于[0.4,0.6)时,假定单元密度为0.5;当单元密度属于[0.6,0.8)时,假定单元密度为0.7;当单元密度属于[0.8,1]时,假定单元密度为0.9,得到均匀密度划分的结果如图1b)所示。采用模糊C均值聚类的方法对宏观单元进行划分,聚类数目为5类,划分后的单元密度分别为[0.08,0.32,0.45,0.63,0.98],结果如图1c)所示。

根据均匀密度划分和聚类划分的结果进行微结构优化设计。优化的目标函数迭代曲线如图2所示。采用均匀密度划分最终迭代的步数为200步,结构柔度为57.16;采用聚类划分最终迭代的步数为202步,结构柔度为52.30,与均匀密度划分方法相比性能提升了8.5%。由此可以看出采用聚类方法划分宏观单元的分布更为合适。

图2 目标函数迭代曲线

2 宏细观灵敏度分析

为了求解上述包含多类微结构的多尺度并行优化模型,需要对宏观优化及细观微结构优化的目标函数进行敏度分析,即目标函数对设计变量的偏导,作为设计变量的迭代更新的依据。

宏观优化模型的敏度为:

(3)

式中ci,j为第i个宏观单元内包含的第j个微结构单元的应变能。

细观微结构优化模型的敏度为:

(4)

在并行优化的后期阶段,由于聚类方法的加入,处于两聚类范围边界的密度值的划分会出现跳动现象,会极大的增加优化时间,所以本文建立聚类结果改进模型,方法为:

(5)

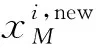
将聚类结果改进模型加入多尺度并行优化模型中,优化的目标函数迭代图变化如图3所示。

图3 聚类结果改进模型比较

从图3中可以看出,在加入聚类结果改进模型后,目标函数在迭代70步以后变得平稳,能更快速的进入收敛,且目标函数最优值变化的很小,证明了改进模型的有效性。

3 多尺度并行拓扑优化设计流程

在确定宏观结构尺寸、单元数量、惩罚函数、聚类数,细观微结构尺寸、单元数量、惩罚函数后,采用模糊C均值聚类的方法对宏观密度进行聚类,得到微结构的密度及位置分布。为了减少聚类边界密度值的跳动现象,使用聚类结果改进模型对聚类后的密度进行修正,对修正后的模型进行宏细观有限元分析,求解宏观结构及细观不同构型微结构的灵敏度。在得到灵敏度信息后,采用优化准则法(Optimality criteria, OC)进行宏细观设计变量的更新,直到目标函数收敛后输出宏观整体结构及细观不同微结构的构型。具体求解流程如图4所示。

4 数值算例及结果分析

在本节中,采用上述构造的“基于聚类的宏细观多尺度并行拓扑优化模型”,针对拓扑优化中经典的悬臂梁、MBB梁、Michell结构问题进行讨论分析,验证构建模型的有效性。在所有模型案例中,结构的边界条件和材料属性都采用无量纲形式,假设杨氏模量为1,泊松比为0.3,为避免刚度矩阵的奇异,令孔洞部分的杨氏模量为1×10-9。

4.1 并行与非并行优化结果分析

基于聚类方法的多尺度非并行优化的主要思想是采用聚类方法对宏观优化后的结果进行聚类,以宏观聚类结果指导细观微结构优化,在细观微结构优化时宏观形状不再改变。与并行优化相比,非并行优化实现较简单,收敛速度较快,但最终得到的结构性能较并行优化得到的结构性能差。

如图5所示,优化模型为悬臂梁结构,几何尺寸L和H分别为300、200 mm,宏观结构设计域离散为30×20个有限单元,每个单元尺寸为10 mm。细观微结构的几何尺寸为10 mm×10 mm,离散为50×50个有限单元,一个宏观单元包含一个微结构。宏观结构左侧全约束,宏观载荷采用无量纲形式F=1,施加在右侧边界的中间位置,优化目标为最大化结构刚度,体积约束为整体结构体积的50%。

多尺度非并行拓扑优化首先需要对宏观结构进行拓扑优化,令惩罚因子pM=1,结果如图6a)所示。采用模糊C均值聚类,聚类数为5。聚类后小于0.1和大于0.9的密度,其微结构会出现极细的杆或极小的孔洞,制造会是个难题,所以当聚类密度属于[0,0.1]时,假定其密度为0,当聚类密度属于[0.9,1]时,假定其密度为1。聚类值为[0,0.32,0.46,0.64,1],结果如图6b)所示。

图6 宏观优化及聚类结果

根据宏观聚类结果进行细观微结构优化,惩罚因子pm≥3即可,在本算例中取pm=3.5,得到的微结构较清晰,过滤半径r=1.5,微结构优化结果如表1所示,包含了体积百分比分别为32%、46%、64%、100%的微结构单胞最优构型图、3×3周期性分布图。整体结构最优构型如图7所示,结构最终柔度C=49.78。

表1 非并行悬臂梁微结构优化结果

图7 非并行悬臂梁结构最优构型

采用多尺度并行拓扑优化对上述悬臂梁模型进行求解,模型尺寸、网格数量、体积分数都保持不变,宏观惩罚因子pM=1,细观微结构惩罚因子pm=3.5,过滤半径r=1.5,微结构优化结果如表2所示,包含了体积百分比分别为28%、48%、74%、100%的微结构单胞最优构型图、3×3周期性分布图。整体结构最优构型如图8所示,结构最终柔度C=37.49。

表2 并行悬臂梁微结构优化结果

图8 并行悬臂梁结构最优构型

可以直观的看出并行与非并行优化的微结构排列基本都是关于横向轴对称分布,这是由于施加的宏观载荷和边界条件关于轴向对称。两种方法得到的整体结构构型在宏观上存在明显差异,且其中3类微结构的体积分数与构型也存在差异,这是由于在并行优化中宏观结构拓扑与微结构拓扑是同时优化的,这与非并行优化存在明显的区别。为了清晰的对并行优化与非并行优化进行比较分析,如图9所示,给出了两种优化方法的目标函数迭代图。

图9 并行与非并行目标函数迭代图

从整个迭代过程来看,在并行多尺度拓扑优化的迭代初期,目标函数的波动较大。这是由于在优化初始阶段,宏观结构变化较大导致聚类结果变化大。两类优化的目标函数都在100代之前达到收敛,在后续的优化中,主要用于进行微结构的形状优化,从而不断优化结构的整体性能。在结构性能(柔度)上,非并行优化的结果为49.78;并行优化的结果为37.49,性能提升了24.7%,这表明基于聚类方法的并行优化模型能很好的提升结构性能。

4.2 聚类数目的影响分析

为了探究微结构种类数ξ对结构性能的影响,分别对具有3类、7类、9类、11类微结构的悬臂梁模型进行多尺度并行优化分析,优化的参数与上述具有5类微结构的悬臂梁优化参数相同,结果如图10所示。其中聚类数目ξ=3微结构单元体积百分比分别[14%,47%,1],最终结构柔度C=39.58;ξ=7的微结构单元体积百分比分别[0,25%,36%,51%,69%,87%,1],最终结构柔度C=37.93;ξ=9的微结构单元体积百分比分别为[0,23%,30%,37%,46%,62%,80%,90%,1],最终结构柔度C=36.48;ξ=11的微结构单元体积百分比分别为[0,20%,27%,33%,39%,47%,58%,71%,83%,90%,1],最终结构柔度C=36.13。

图10 具有不同类微结构的悬臂梁最优构型

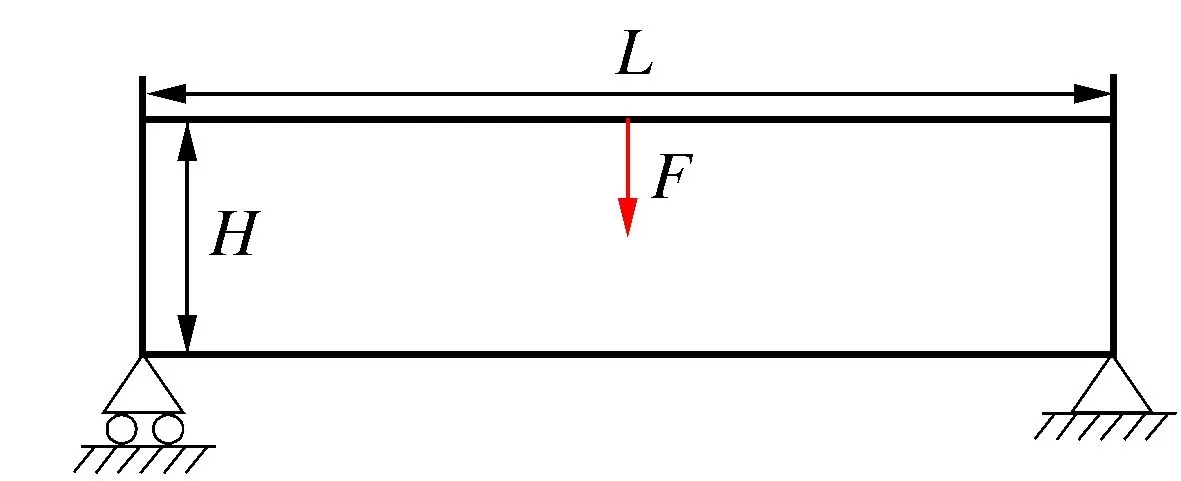
图11 MBB梁结构设计域

分析具有3类、5类、7类、9类、11类微结构的悬臂梁模型优化结果,可以发现宏观结构整体构型比较类似,且当微结构数目逐渐变大时,整体构型差别逐渐变小。不同类微结构的悬臂梁优化结果如表3所示。

表3 具有不同类微结构的悬臂梁优化结果

由表3可以看出,随着微结构数目的增加,结构最终柔度在减小,这表明增加微结构的数量可以提升结构的性能,符合预期结果,但同时也会降低优化的效率,增加优化的时间成本。综合分析比较不同类微结构的优化结果,可以看出当微结构数目大于5类后,性能增长较慢,且迭代步数与平均每步计算时间较长,因此选用5类微结构可以代表具有多类微结构的多尺度并行拓扑优化结果,在下述算例的微结构数目取5类。

4.3 MBB梁算例分析

所建模型的有效性。MBB梁结构尺寸L和H分别为800 mm、200 mm,宏观结构设计域离散为80×20个有限单元,每个单元尺寸为10 mm。细观微结构的几何尺寸为10 mm×10 mm,离散为50×50个有限单元,1个宏观单元包含1个微结构。左下角简支,右下角固支,宏观载荷采用无量纲形式F=1,施加在上端中点处竖直向下。优化目标为最大化结构刚度,体积约束为整体结构体积的50%。

采用多尺度并行优化模型对MBB梁结构进行优化分析,宏观惩罚因子pM=1,细观微结构惩罚因子pm=3.5,过滤半径r=1.5,微结构优化结果如表4所示,包含了体积百分比分别为26%、46%、84%、100%的微结构单胞最优构型图、3×3周期性分布图。整体结构最优构型如图12所示,结构最终柔度C=44.57。

表4 MBB梁细观微结构优化结果

从MBB梁宏观结构最优构型可以看出,微结构的分布关于设计域左右对称,且在宏观载荷与约束施加处以实体微结构为主,这符合受力特点。为了更加清晰的显示微结构之间的连接性问题,将体积百分比分别为26%、46%、84%的微结构放在一起讨论分析,如图13所示。

图13 不同构型微结构连接示例

从图13中可以看出,不同构型的微结构之间的连接情况良好。这是由于在多尺度并行优化过程中,宏观结构分析与细观微结构优化是同步进行的,消除了连接性问题。

优化过程的目标函数迭代曲线如图14所示,从图中可以看出,目标函数在前期迭代不平稳,但总体趋势是减小的,这是由于前期优化中宏观结构变化较大导致聚类结果变化较大。迭代过程在100步前达到收敛,后续主要是对微结构进行形状优化,目标函数变化较小。

图14 MBB梁结构目标函数迭代图

4.4 Michell结构算例分析

如图15所示,以Michell结构为优化对象讨论上述所建模型的有效性。Michell结构尺寸L和H分别为500 mm、200 mm,宏观结构设计域离散为50×20个有限单元,每个单元尺寸为10 mm。细观微结构的几何尺寸为10 mm×10 mm,离散为50×50个有限单元,1个宏观单元包含1个微结构。宏观结构的左下角固支,右下角简支,宏观载荷采用无量纲形式F=1,施加在底部中心处竖直向下。优化目标为最大化结构刚度,体积约束为整体结构体积的50%。

图15 Michell结构设计域

采用上述构建的模型对Michell结构进行优化分析,宏观惩罚因子pM=1,细观微结构惩罚因子pm=3.5,过滤半径r=1.5,微结构优化结果如表5所示,包含了体积百分比分别为27%、56%、83%、100%的微结构单胞最优构型图、3×3周期性分布图。整体结构最优构型如图16所示。结构最终柔度C=26.75。

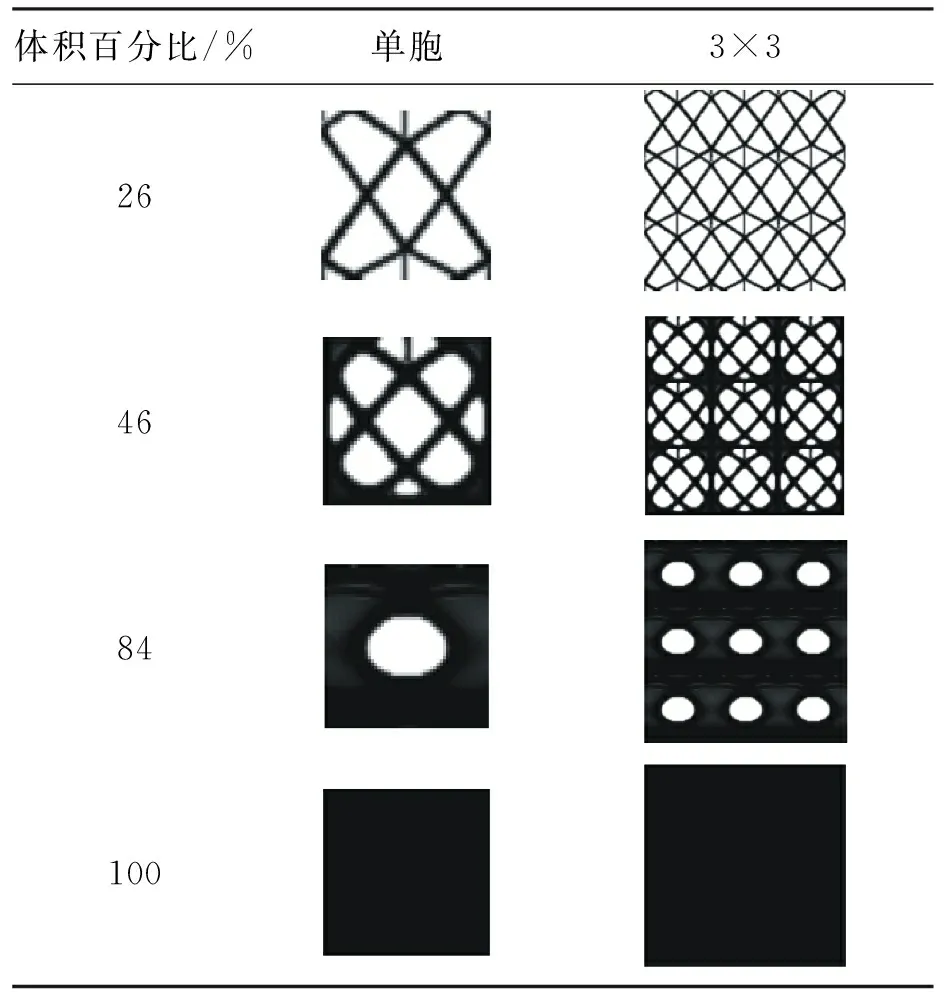
表5 Michell细观微结构优化结果

图16 Michell结构最优构型

图16可以看出,微结构的分布关于宏观结构纵向轴对称,且在底部中间部分和边界条件施加处以实体微结构为主,这符合宏观载荷及边界条件分布规律,微结构之间的连接性不存在问题。

优化过程的目标函数迭代图如图17所示,从图17中可以看出主要变化发生在前50步迭代中,这是由于在前50步迭代中宏观结构聚类结果及微结构构型变化较大。后续的优化主要对微结构进行形状优化,优化过程较平稳。

图17 Michell结构目标函数迭代

综上所述,悬臂梁结构、MBB梁结构、Michell结构的多尺度并行优化过程清晰的展示了所建立优化模型的有效性。

5 结论

1) 提出了一种同时考虑结构宏观性能和细观微结构性能的多尺度并行拓扑优化设计方法。通过对宏观优化结果的聚类,得到不同类型微结构的体积及位置信息,从而指导细观微结构的优化设计,并把优化的微结构重新填充到宏观结构中,再次评价宏观结构的性能;依次循环,直到获得最优的宏观结构及细观的微结构。

2) 为提高计算效率、降低计算时间成本,采用聚类方法减少了微结构类型;同时针对优化后期聚类边界密度值的划分波动导致目标函数迭代不收敛问题,提出聚类结果改进模型,有效解决了聚类波动问题,使得目标函数快速收敛。

3) 采用基于聚类方法的非并行优化方法与并行优化方法分别对悬臂梁结构进行了优化设计,结果显示并行优化相比非并行优化结构性能提升了24.7%,说明了并行优化能较大幅提升结构性能。

4) 应用本文方法分别对悬臂梁、MBB梁、Michell结构进行了结构优化设计,从优化结果明显看出论文所提方法的正确性和有效性,这为同时考虑宏细观结构特性的拓扑优化设计提供了科学的设计方法。