学为中心,让数学理解更深刻
——“用转化的策略求和”教学实践与思考
江苏省无锡市新吴区旺庄实验小学 钱 慧
“用转化的策略求和”是苏教版数学五年级下册的内容,是学生在学习了图形的周长、面积的转化的基础上学习的内容。转化是一种常见的、非常重要的解决问题的策略,也是一种包含着数、形、式互相转化的数学思想,让数学知识从复杂变简单,从陌生变熟悉,从抽象变具体,从未知到已知,从而解决问题。
教学是不断学习、不断探索的过程。笔者深刻反思后总结出,要让学生真正理解转化的过程、形成转化的意识、掌握转化的方法,打造基于学生理解的“发现”课堂,教师就要立足学生的成长规律和主体地位,关注学生理解能力的提升,真正体现“学为中心”,让“发现”发生在数学课堂上。
一、学习经验,激发理解基础
生1:分子都是1。
生2:后一个数的分母是前一个的2倍。
师:怎样计算这样的算式呢?
生1:通分,把异分母分数加法转化成同分母分数加法。
生2:把分数加法转化成小数加法。
师:原来转化的策略在计算中也很好用。
教师从学生的学习经验出发,让学生已有的学习水平成为新学习的起点。课前,学生完成“研学单”——基于核心学习目标设计的激活学生已有知识经验的前置性学习任务。学生凭着已有经验,能把转化成同分母分数加法、转化成小数加法、转化成图形。教师从简单的题目入手,引导学生建立分数与小数之间的联系、分数与图形之间的关系,从而让他们能够想到用结合图形的方法来初步表示分数加法。在此基础上,教师让学生计算例2:=______________。课前,学生运用已有经验来计算,课上再进行交流。大部分学生用通分的方法计算,少部分学生把分数转化成小数再计算,也有几个学生受到可以将转化成图形的启示,能想到用来计算。不同的学生的学习基础水平不同,因此,教师要最大限度地激发学生的学习经验,让学习能力一般的学生能跳上个台阶,让学习能力强的学生思维更活跃。从学生课前研学单的完成情况来看,大部分学生具备了计算转化的理解基础,为后续的主动学习打好了基础。
二、核心问题,提升理解能力
教师出示历学单(见图1)。
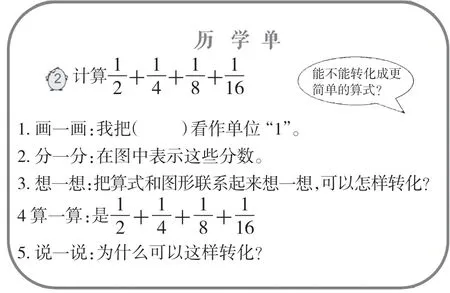
图1
师:为什么可以这样转化呢?我们请几位同学来展示一下历学成果。生1:我把正方形看作单位“1”,平均分成2份,每份是,再把平均分成2份,每份是,再把平均分成2份,每份是,再把平均分成2份,每份是的和就是单位“1”减去空白部分
生3:我把一条线段看作单位“1”来平均分……
(1)练一练。
师:同学们,按照加数的特点,接着可以加多少?完成拓学单第1题。
师:谁来说一说这道题是用了什么策略来计算的?
师(小结):通过画图可以知道,这四个加数的和=单位“1”-空白部分,所以原来的加法算式可以转化成。
教学中,教师要从学生的学习能力出发,给学生创设更多的学习和表达的机会。课中,教师让学生探究“历学单”——基于学习内容的核心问题设计的探究性学习任务,从“能不能转化成更简单。的算式”这一核心问题算起,让学生经历“画一画、分一分、想一想、算一算、说一说”五步历学活动,通过一系列的问题串,让学生经历“怎样转化、为什么可以这样转化”的数学理解全过程:图形对应,抽象变具体,分数可以用图形来表示,分数加法也可以用图形来表示,抽象的数借助图形就变得形象化,直观全面,整体性强,更容易找到问题解决的突破口。数形结合,使复杂变简单,让学生感受到原来数与形可以转化,加法可以转化成减法,数学学习原来这么简单、这么神奇,让学生容易找到问题的关键所在,从而解决问题;数学表达,建立模型,在看图(圆、正方形、线段等不同的图式)说话的表达交流过程中,让每个学生都理解转化的过程:=单位“1”-空白部分=。学生在动手做、动口说的过程中理解了“怎样转化、为什么可以这样转化”,从初步理解走向深刻理解,使理解水平逐步提升。
三、变式比较,深化理解水平
教师出示拓学单(见图2)。

图2
师:为什么可以这样转化?
(2)想一想,如果再继续加下去,可以怎样计算?
师:通过刚才的转化,你们发现什么规律了吗?
(3)拓展。
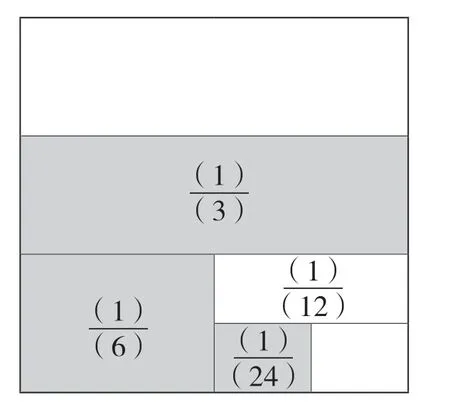
图3
师:这里与例题有什么区别与联系?
生2:加数之间都是一半的关系,可以画图,都是用单位“1”-空白部分。师(小结):每一个加数都是前一个加数一半的连加,都可以转化成“单位‘1’-空白部分”的减法来计算。在解决问题时,我们要养成运用数形结合策略的意识。
(4)连续奇数的和
师:观察图4中每个图形圆的排列规律,每个图形中圆的个数可以怎样计算?

图4
生:第一组是1个,第二组有4个,1+3=4,第三组有9个,1+3+5=9,第四组有16个,1+3+5+7=16。
师:这些加法算式有什么特点呢?
生:从1开始的连续奇数相加,用加法可以求圆的个数。
师:看一看图,还可以怎样计算?
生:每一组是一个正方形,我们也能用乘法来求圆的个数。第一组,1个圆就是1行1列,就是1×1,第二组,是2行2列,就是2×2,第三组是3×3,第四组是4×4。
师:从1开始的连续奇数相加,可以怎样转化?
生1:从1起的几个连续奇数相加,可以转化成乘法来计算。
生2:有几个加数就是几乘几。
师(小结):从1起,不管有多少个连续奇数相加,我们都可以转化成奇数个数的平方。原来加法还能转化成乘法。
(5)课后延伸
师:从1起连续奇数的和有这样的规律,那从2起连续偶数的和会有什么规律呢?课后有兴趣的同学可以画图研究。(见图5)

图5
教学中,教师从学生的学习水平出发,给学生设计有指向性的练习来消化和巩固所学的转化策略。课后,学生完成“拓学单”——有目的、有指导、有层次、有提升的练习设计单。从例题出发,教师接着出题。学生通过观察比较得出:从起,依次加上前一个分数一半的数,都可以转化成“1-最后一个加数”的减法来计算。为了不让学生形成思维定式,教师又让学生完成,学生也能够画图解答。学生通过图形结合解答了“1+3+5+7+9=5×5=25”,并发现:从1起,连续奇数的和可以转化成奇数个数的平方,加法还能转化成乘法。教师在此基础上让学生进行思维拓展:2+4+6+8+10=?连续偶数的和可以怎样转化呢?教师从知识点间的联系入手,抓住知识间的连接点,通过变式练习,由简单到综合,由基础到拓展,由顺向到逆向,由模仿到自主,通过不同题组的比较联系,增强了学生的转化意识,提高了学生的转化能力,让学生理解、体会到数学学习的有趣、有用和富有挑战性,满足了不同层次学生的学习理解水平。
学生学习数学的过程就是发现知识的理解过程。教师要立足学生的理解水平,激发学生学习的内驱动力,让发现真实发生,让理解真正深刻;要关注学生的学习经验,相信学生的能力,放手让学生去思考、去探究;要有意识地引导学生,围绕核心问题创设学生容易操作、富有挑战性的学习活动,把课堂真正还给学生,让学生主动去理解数学;要设计富有层次性的练习,让学生在比较中迁移所学知识,形成自主分析问题、解决问题的能力,促进学生数学核心素养的不断提升。

