薄盘工件不平衡量在线测算及去重试验研究*

张仕海，朱冶诚

（1.天津市高速切削与精密加工重点实验室，天津 300222；2.天津职业技术师范大学，天津 300222）

薄盘类零件是回转机构上常用的零部件类型之一，该类零件具有较大的径厚比，即使很小的不平衡质量也可能形成较大的不平衡量。关于薄盘类零件的平衡主要有两种方法：（1）在专用的动平衡机上进行工件不平衡量的检测，然后在数控机床或其他校正设备上进行不平衡量的校正[1]。该方法的检测与校正环节分离、设备成本较高、平衡效率较低，同时工件的反复装卡也会带来一定的安装误差。（2）20 世纪50 年代出现的全自动动平衡机实现了不平衡量检测和校正工艺的集成，提高了工件的平衡效率和精度[2–3]。该方法仍需要较高的设备成本，也不能实现工件加工与平衡工艺的集成。基于薄盘工件结构特点，提出工件加工、不平衡量的在线测算与去重校正三工序集成的理念，并从理论上、技术上探讨了方法的可行性。

理论上，基于夹载工件前后机床主轴不平衡振动信号的变化，以及不平衡激励与振动响应之间影响系数的线性可逆原理，可以实现工件不平衡量在线测算。影响系数法属于转子动平衡技术中经典的试验方法，目前应用的关键在于影响系数精度提高及其自适应问题。Dyer 等[4]提出了一种利用指数加权平均法来减少测量噪声和系统非线性影响的递归在线系统辨识方法，提高了影响系数的自适应性。Zhang[5]提出了一种基于层次贝叶斯方法的自动动态影响系数标定和在线更新方法。樊红卫等[6]通过引入增益因子提高平衡迭代过程稳定性，并引入遗忘因子实现影响系数在线估计，构建了单平面在线自适应平衡算法的数学模型。相关研究在一定程度上解决了因转子系统动力学特征参数发生改变而导致原来测算的影响系数不准确问题。

技术上，现代复合数控机床（如车铣复合）具备主轴准停、刀具定位、精确去重等功能，再附以不平衡振动检测与分析系统，完全满足工件不平衡量的在线去重要求。工件不平衡量在线去重技术包括去重建模和去重控制。去重建模是通过数学模型将工件不平衡量转化为指定位置的待去重体积，进而计算刀具的进给量和轨迹。刘健等[7]考虑去重质量在转子周向、径向、轴向的分布，以及圆周上分布的槽对实际去除不平衡量的影响，建立较精确的R 型铣削去重模型，以去除金属量最少为目标函数，建立了单排刀具和多排刀具的V 型铣削去重模型。曾胜等[8]提出一种V 型铣刀切削去重简化模型及基于此模型运用线性插值方式的去重切削控制方案，其包括切削去重建模和实时参数化插值两部分。殷苏民等[9]根据转子的齿槽分布对铣削量和铣削方位产生的影响，建立数学模型，用Newton 迭代求解，对相位误差进行修正，并对相应的幅值误差进行补偿。刘冰[10]以车铣复合机床对不平衡薄盘工件的去重应用为目的，建立了适用的内（外）圆弧铣削去重模型。去重控制是在工件指定位置去除适当材料的过程，具体实现需要根据数控机床功能来设计。

1 基于影响系数的薄盘工件不平衡量在线测算与校正方法

1.1 薄盘工件不平衡量在线测算

本研究选取的薄盘类工件具有较大的径厚比（≥5），工件不平衡量可以看作分布在同一平面内。因此，可将工件不平衡量等效到机床卡盘的端面上，基于单平面影响系数线性可逆原理，通过测量主轴空载及带工件条件下不平衡振动的变化而间接测算工件不平衡量，该方法的基本原理与步骤如下。

（1）在主轴的适当位置处设置振动检测点，调整主轴转速至平衡转速n，在卡盘不带工件的情况下测量主轴振动及基准信号，以平衡转速为基频，提取主轴初始不平衡振动信号，设其向量为V0。

（2）将试重工件（已知不平衡量的向量为U）装于卡盘上锁紧，调整主轴转速至平衡转速n，重新测量并提取主轴不平衡振动信号，设其向量为V1，则工件所处端面相对于测点的影响系数表示为

试重试验后，初始参数V0及影响系数R可作为控制参数，用于工件不平衡量的在线估算。如设卡盘带工件后实测不平衡振动信号向量为V2，则基于影响系数线性可逆原理，可计算出工件不平衡量为

理论上，基于式（2）不平衡量的测算，在薄盘工件上适当位置施加反向不平衡量–Ux即可实现工件不平衡量的在线校正。

1.2 校正误差分析

（1）测量误差分析。受不平衡振动信号测量与计算误差、影响系数测量与计算误差等因素的影响，工件不平衡量逆向测算值与真实值之间不可避免地存在一定的误差。以不精确的测量值作为校正目标，校正后必然会残余一定的不平衡量。设薄盘工件不平衡量的实际值及在线测算值分别为，则工件不平衡量校正后的残余不平衡量形成原理，如图1（a）所示。

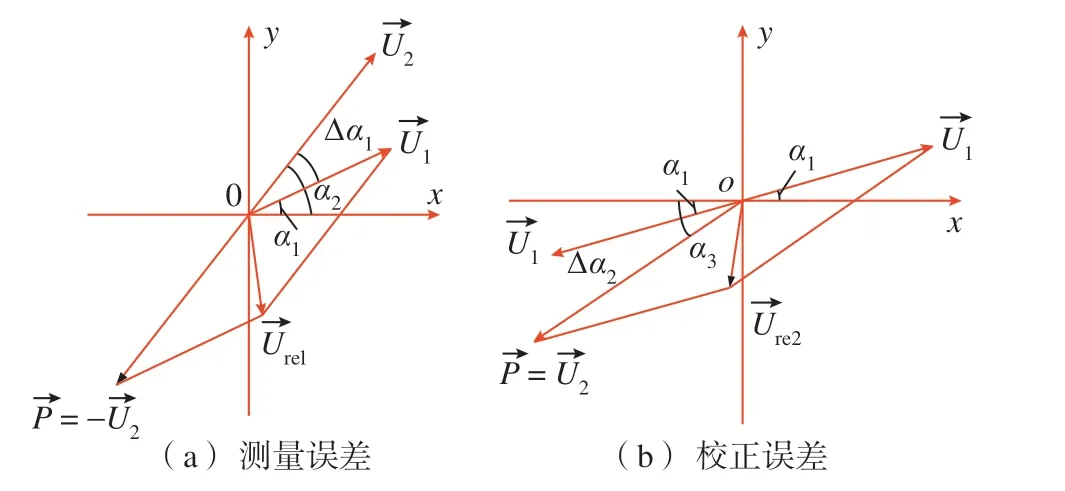
图1 测量与校正误差分析Fig.1 Measuring and correcting errors analysis

由图1（a）中的向量关系可以计算出工件不平衡量校正后的残余不平衡量幅值Ure1为

式中，Δα1=α2–α1。

（2）校正误差分析。工件不平衡量在线校正主要在数控机床上直接进行，其校正误差主要来源于去重建模过程中的理想化所产生的计算误差、工件材料不均匀性及密度差异、去重过程中所产生的控制误差等。设工件理论所需校正量为–U1，实际的校正量为U3=U3∠α3，则工件校正后的残余不平衡量形成原理如图1（b）所示。由图1（b）中的向量关系可以计算出工件校正后残余不平衡量的幅值Ure2为

式中，Δα2=α3–α1。

由式（3）和（4）可以看出，如果Δα1≈0，Δα2≈0，说明测量和校正的方位误差较小。由于去重属于不可再生校正，此时应防止过大校正而对工件造成不可修复性的损伤。

当Δα1与Δα2数值较大时，相位误差对校正后工件残余不平衡量幅值的影响是主要的，该现象可称为误校正。

在实际应用中，工件不平衡量的测算及校正误差总是相互叠加的。

2 薄盘工件不平衡量在线测算及校正试验

2.1 试验系统设计

为便于对薄盘工件的不平衡量进行调控，设计如图2（a）和（b）所示的阶梯状薄盘工件，图2（a）中A1为工件不平衡量模拟调节面，A2为工件不平衡量模拟校正面，A1、A2平面内等效不平衡量的调整均通过4 组径向均匀分布的螺栓–螺母组件来实现。每个螺栓–螺母组件的螺栓拧入工件相应的螺纹孔内，并通过锁紧螺母实现组件锁紧，调节两个扁螺母距离薄盘工件中心的距离，即可实现该轴不平衡量的调节。

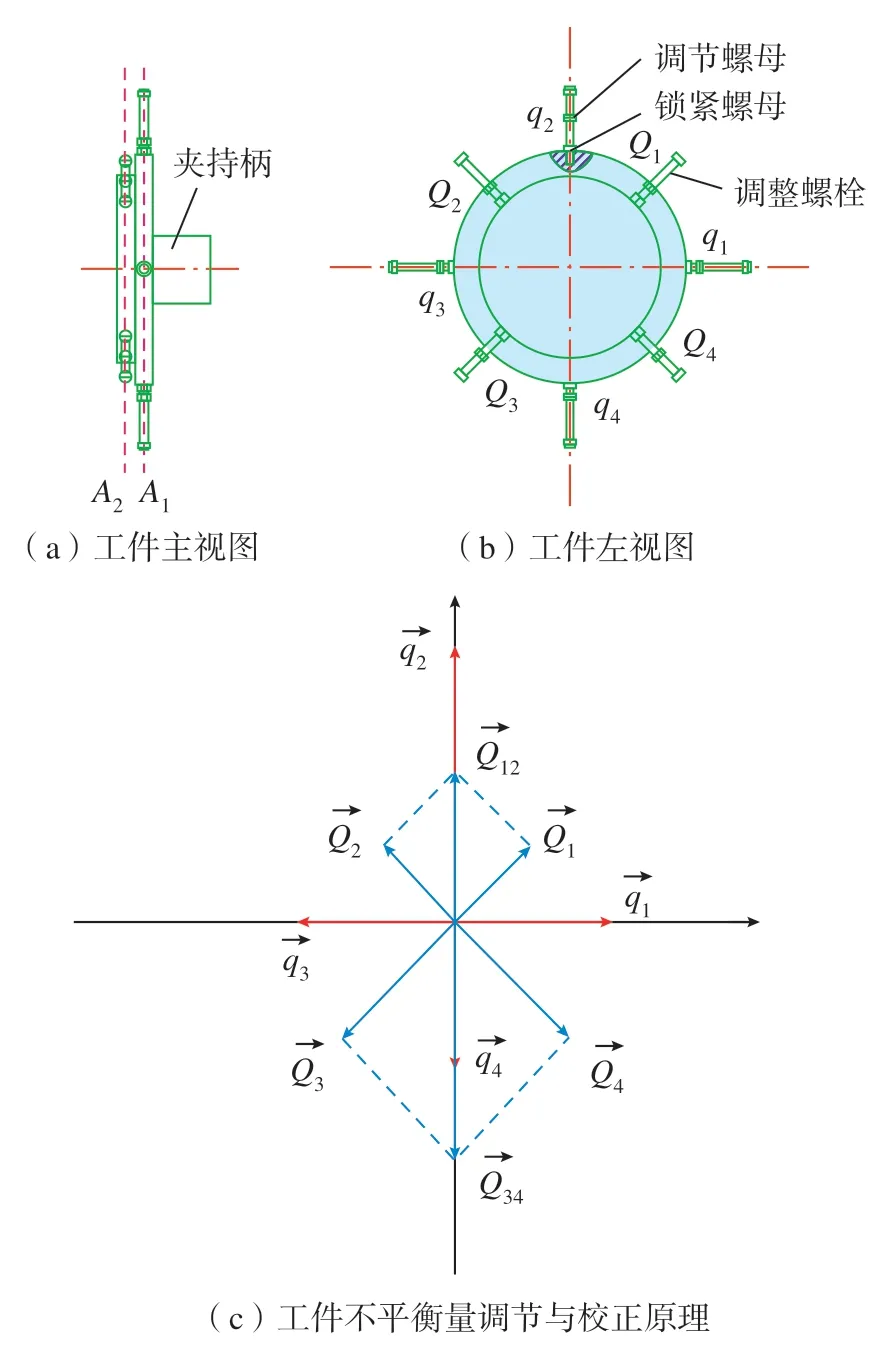
图2 薄盘工件及其不平衡量调节机构Fig.2 Thin-disc workpiece and its unbalance vector adjusting mechanism

图2（a）所示工件具有较大的径厚比，A1、A2平面内的不平衡量可以等效于一个平面中，其不平衡量的调节和校正原理如图2（c）所示。设将调节螺母组q2外移一定距离，其所产生的不平衡量可以通过调节螺母组Q3、Q4的合成不平衡量进行校正。

理论上，分别对A1、A2平面内4 个方向上调节螺母进行适当调节，即可在360°范围内对工件不平衡量进行模拟调节和校正。模拟车床主轴基本结构制作的试验系统如图3 所示。图3 中主轴系统由主轴、卡盘、前/后支撑等单元构成，主轴系统通过连轴器与伺服电机输出轴直接相连，伺服驱动系统可实现电机+主轴系统转速的调控。薄盘工件的夹持柄穿入卡盘中心孔内，并被卡盘卡爪紧固夹持。通过两个电涡流位移传感器分别监测主轴前后端振动信号，通过电磁接近开关监测主轴基准信号，所有传感器信号均通过信号采集卡采集（NI PCI–4472）。

图3 工件不平衡量在线测算与校正试验系统Fig.3 Testing and correcting experimental system of unbalancing thin-disc workpiece

2.2 校正试验

为便于信号分析，试验中实施整周期信号采样。基于单平面动平衡原理，仅通过一个测点即可逆向测算工件不平衡量。通过试验测算，前端测点振动对工件不平衡量的激励比较敏感，这里将主轴前端振动信号作为分析与控制的目标。

考虑到试验的安全性，这里以900 r/min 作为平衡测试转速。图4 为主轴空载条件下，传感器所监测的整周期信号。采用最小二乘法[11]拟合主轴前端不平衡振动信号为 11.324 μm∠–42.77°。该不平衡振动主要是由主轴本体不平衡、卡盘及其与主轴连接不平衡、联轴器不平衡、安装不平衡、电机轴及电机安装不平衡、基准附加物等复合而成。

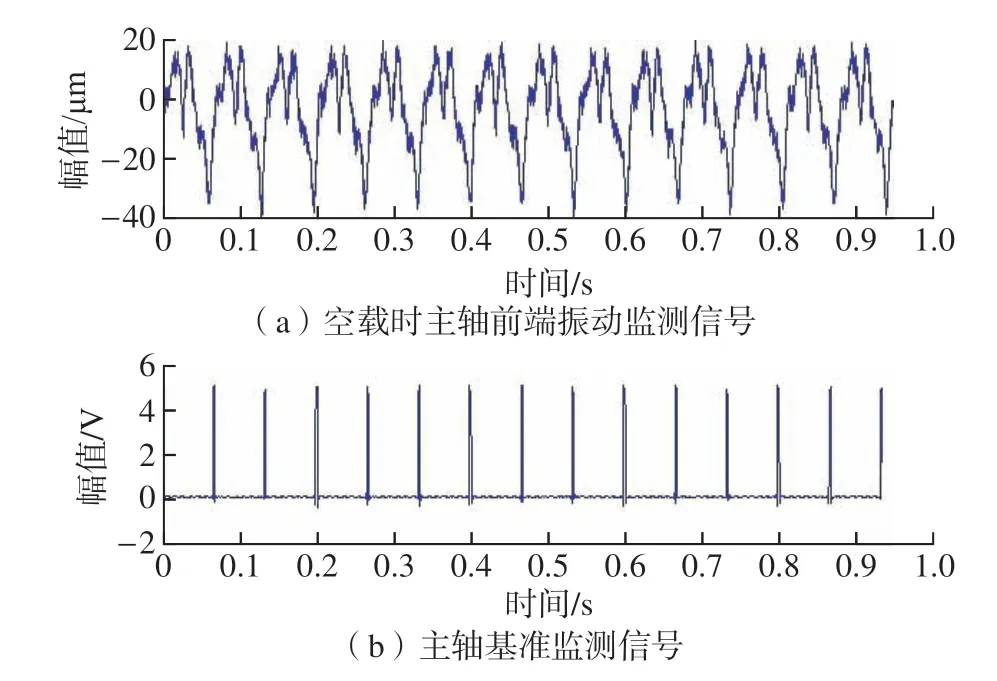
图4 主轴振动监测信号Fig.4 Vibration monitoring signals of spindle

为测算工件不平衡相对主轴振动测点的影响系数，这里将A1平面内与基准同方向的螺栓拧出5 mm，并在动平衡机上测量工件不平衡量为14.52 g·cm∠0°。在平衡转速下所监测的主轴前端振动信号如图5 所示。

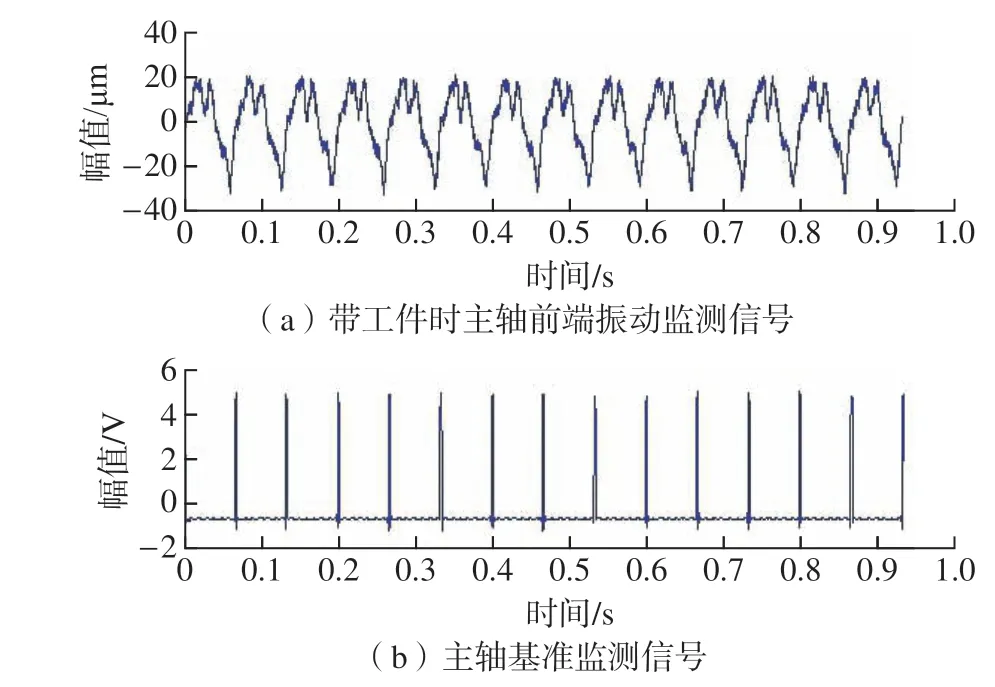
图5 工件–主轴耦合振动监测信号Fig.5 Vibration monitoring signals of spindle with workpiece

为使试验数据具有一定的持续性和规律性，这里随机选取5 组试验数据并计算影响系数（表1）。由表1可以看出，5 次试验的不平衡振动信号及影响系数的测算值均存在一定的差异，说明信号测量与计算过程中存在一定的误差。

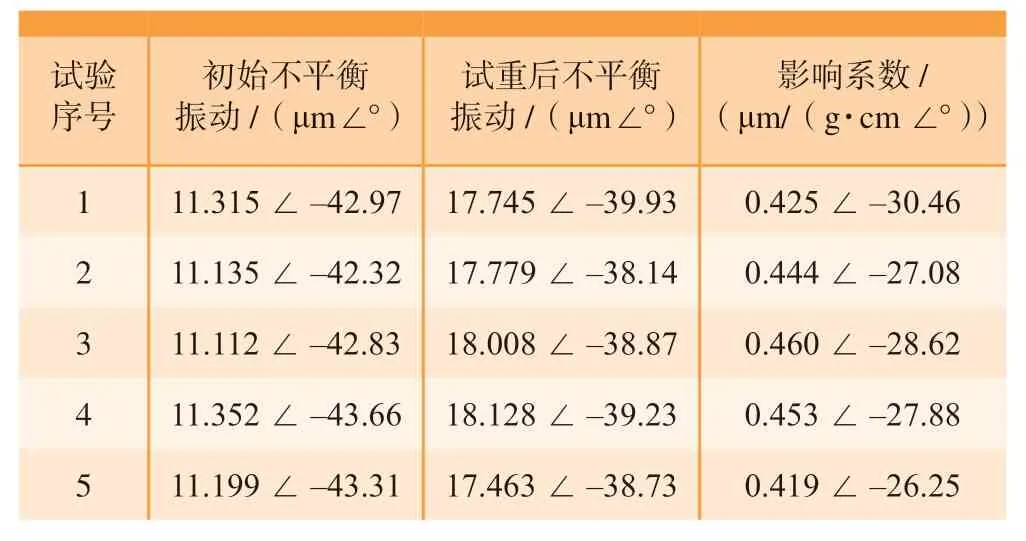
表1 选取的5 次试验数据及影响系数Table 1 Experimental data and influence coefficient of 5 times

为考察工件不平衡量的逆向测算精度，这里改变试重方向，即将A1平面内与基准反向的调节螺母拧出一定距离，在动平衡机上测量工件不平衡量为 14.52 g·cm∠180°。重新进行试验并测算工件的等效不平衡量，测算结果如表2 所示。

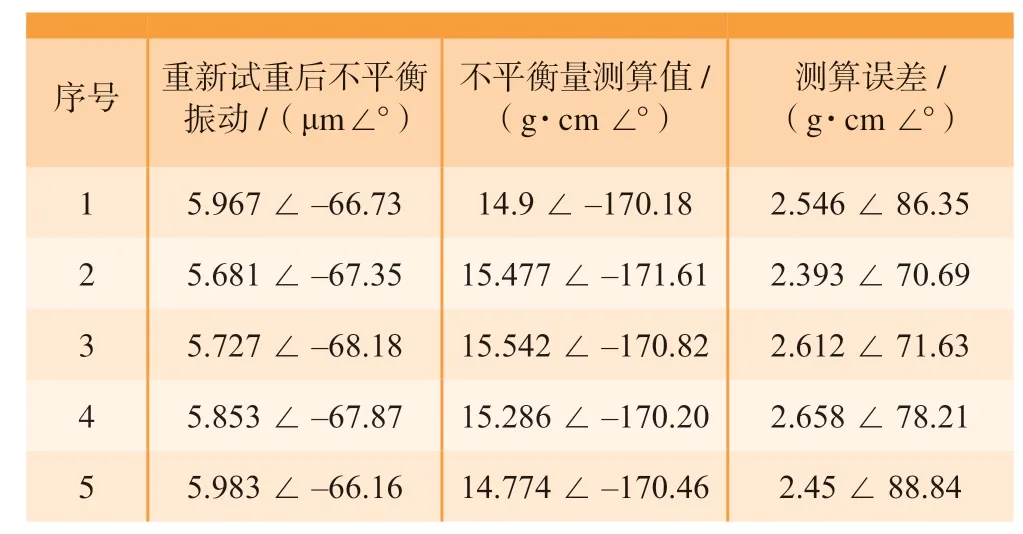
表2 工件不平衡逆向测算结果Table 2 Reverse calculation results of workpiece unbalance vector

表2 中的测算误差等于工件不平衡量的理论值与测算值的向量差。根据表2 测算结果，调整A2平面内相应的调整螺母，实现对工件不平衡量的校正。工件不平衡量的校正结果如表3 所示。

表3 工件不平量的校正Table 3 Correction of workpiece unbalance vector

表3 中的校正误差等于校正后的残余不平衡量减去测算误差。等效校正量等于表3 中的校正误差减去工件不平衡量的理论值。分析表2 和3 数据可得出以下结论。

（1）基于主轴加载工件前后不平衡振动信号的变化，可以相对精确地估算出薄盘工件的不平衡量。

（2）由于信号测量和分析存在一定的误差，致使工件不平衡量存在一定的测算误差，且同一时段内的测算误差相对稳定。

（3）在工件残余不平衡量检测后，可以通过在线校正的方式减少工件残余不平衡量，其校正精度受不平衡量测量和校正误差的双重影响。

3 结论

论文围绕薄盘类工件不平衡量在线测算及模拟校正开展了试验研究，对实际应用具有以下指导性意义。

（1）通过对盘类工件加工过程中不平衡量的在线测算，可以实时监控工件不平衡量的变化状态，减少因工件装卡不当、加工工序错误等问题而导致工件不平衡量异常变化。

（2）通过对多工件加工后残余不平衡量在线测算，可以在无动平衡机等专用测试设备条件下对工件平衡质量进行实时评估。

（3）工件不平衡量在线校正可以在无动平衡机等专用校正设备条件下，对工件加工后的残余不平衡量实施校正，可以进一步挖掘数控机床潜能，节省盘类工件动平衡成本。